生灭过程的两类拟平稳分布

朱依霞

(湖南财政经济学院 数学与统计学院，长沙 410205)

近年来，马尔可夫过程的拟平稳分布越来越受到重视[1-4].拟平稳分布常常被用来分析随机系统的长期行为，这些系统在某种意义上最终会停止，但系统在停止之前可能会出现一个平稳期.马尔可夫过程的拟平稳分布的研究最早可以追溯到俄罗斯数学家Yaglom的工作，他首次提出了Galton-Watson分支过程中的于次临界情况下总是存在极限条件分布[5].后来Darroch等[6-7]、Flaspohler[8]以及Ferrari[9]等为推动拟平稳分布理论的发展做出突出贡献.Darroch等[6-7]研究了有限状态空间的马氏链的拟平稳分布；Flaspohler[8]研究了初始分布为单点集时连续时间的马氏链的拟平稳分布；Ferrari等[9]创新性地利用更新方法研究了连续时间的马尔可夫过程的拟平稳分布存在的充要条件.拟平稳分布还不断出现在流行病、生态学、可靠性理论、遗传学等背景中，也一定程度推动了拟平稳分布理论的发展.生灭过程，是一类特殊的但又重要的马尔可夫过程.生灭过程的拟平稳分布已研究得相当广泛和深入[2,10-11].但生灭过程的拟平稳分布仍然存在一些待解决问题，这在毛永华[3]中有阐述.

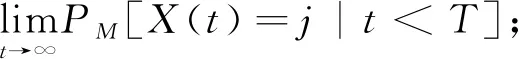
其中Xj(t)为马尔可夫过程X在时间t前停留状态j的时间，M={mi,i∈C}为初始概率分布.对于第1类一般形式的拟平稳分布，生灭过程存在唯一的拟平稳分布当且仅当过程为流入边界，同时这个唯一的拟平稳分布吸引所有的初始分布[10-11].本文研究生灭过程的另两类拟平稳分布的存在性、唯一性和吸引域问题.Flaspohler[8]讨论了初始分布为单点集时，这3类拟平稳分布都是唯一的，本文得到从任意初始分布出发时，拟平稳分布仍然是唯一的.本文的主要结论定理1和定理2与文献[12]虽是相同的，但本文利用对偶方法和拟平稳分布的定义证明两类拟平稳分布的存在性、唯一性和吸引域，其方法和思路来源于Zhang等[10].

1 生灭过程与主要结论

令状态空间为E≡{0}∪C，C≡{1,2，…}是非瞬时类，状态0为吸收态.X={X(t),t≥0}是连续时间的马尔可夫链，设该过程的转移概率矩阵为 P(t)=(Pij(t))=(P[X(t)=j|X(0)=i])，

X为E上的生灭过程，它的q-矩阵为Q≡(qij,i,j∈E)，

λn,μn≥0,n≥0分别为X的出生率和死亡率.在研究拟平稳分布时，一般假设状态0为吸收态，假设λ0=μ0=0,且λn>0,μn>0,n≥1，还假设Q是保守的，Q中所有状态都是稳定的，且状态集C对最小Q-函数F不可约.

令T=inf{t≥0:X(t)=0}为灭绝时间，当X到达吸收态0，则过程被吸收.

本文假设A=∞，此时R=∞，最终灭绝的概率为Pi(T<∞)=1[11].令αk=Pk[∃r>0使得X(r)=0],k∈C.

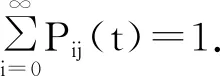
设{Qn(x),n=1,2,…}是Q的右特征向量，

称{Qn(x)}为生灭多项式.生灭过程的转移概率Pij(t)满足一定条件时可以写成如下表达式：

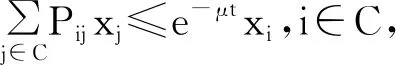
则称{mi,i∈C}为Pij(t)在C上的μ-次不变测度，称{mi,i∈C}为Pij(t)在C上的μ-不变测度当且仅当等式成立.

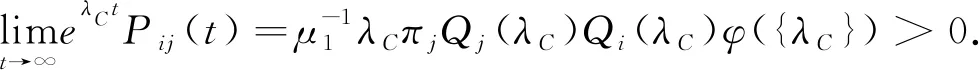
命题1[13]设λC为C的衰减参数，Pij(t)为转移函数.设μ∈[0,λC]，并令{ui,i∈C}和{vi,i∈C}为两组大于零的常数.

(i) 若存在μ-次不变测度{mk,k∈C}满足:

(ii) 若存在μ-次不变向量{xk,k∈C}满足:

(iii) 若存在μ-次不变测度{mk,k∈C}和μ-次不变向量{xk,k∈C}使条件(3)和(4)同时满足.并且还满足条件(a)或(b).(a) supk∈C|uk|/mk<∞,(b) supk∈C|vk|/xk<∞.

引理3[10]生灭过程X存在唯一的平稳条件的拟平稳分布，且这个唯一的拟平稳分布吸引C上所有的初始分布，当且仅当X满足A=∞,S<∞，也就是说，对C上任意的概率测度M={mk,k∈C}，有

性质1[14]令P(t)为任意Q-函数，设m是C上的一个概率测度.则m是C上的拟平稳分布当且仅当对某个μ满足0<μ≤λC，m是C上关于P(t)的μ-不变测度.

显然，若m是C上的唯一的拟平稳分布，那么m是C上关于P(t)的λC-不变测度.

下面给出本文的主要结论.

定理1若X满足A=∞,S<∞，则生灭过程X存在唯一的双重极限条件的拟平稳分布，吸引C上所有的初始概率分布，即对C上任意的概率测度M={mk,k∈C}，有

定理2若X满足A=∞,S<∞，则生灭过程X存在唯一的极限条件平均比值的拟平稳分布，且吸引C上所有的初始概率分布，即对C上任意的概率测度M={mk,k∈C}，有

注：定理1和定理2分别得到了生灭过程在A=∞,S<∞条件下，从分布出发的双重极限条件的拟平稳分布和极限条件平均比值的拟平稳分布不仅存在而且还是唯一的，并且得到极限的具体表达式.上述定理与朱依霞[12]中结论是相同的，但朱依霞[12]中关于生灭过程的结论是作为随机单调过程的一个例子出现的.下面本文将利用拟平稳分布的定义证明上述定理.

2 主要结论的证明

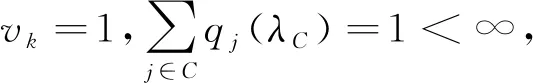
令M={mk,k∈C}为任意初始分布.由引理1，若A=∞,S<∞，则存在某个常数K使得Qi(λC)≤K，因此，

又因为{Qi(λC)}是一个λC-不变向量，故在命题1(ii)中令xk=Qi(λC),uk=mk，利用引理2得

令vk=1，并由引理1，Qi(λC)≤Qi+1(λC)，得:supk∈C1/Qk(λC)=1/Q1(λC)=1<∞，根据命题1(iii)可得

再由引理2得

综合式(5)～(7),对j∈C，得双重极限条件的拟平稳分布:

定理2证明利用洛必达法则以及式(5)～(7)得

3 实例

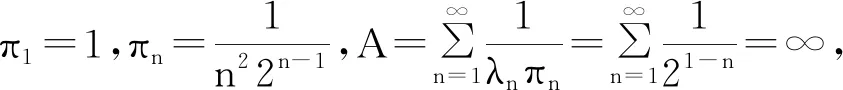
从引理3可知，该过程存在唯一的拟平稳分布，且任意的初始分布都在X的拟平稳分布的吸引域中.从定理1和定理2可得，该过程也只存在唯一的双重极限条件的拟平稳分布和唯一的极限条件平均比值的拟平稳分布，并且初始分布都在双重极限条件的拟平稳分布和极限条件平均比值的拟平稳分布的吸引域中.

4 结语

本文证明了具有流入边界的生灭过程的两类拟平稳分布的存在唯一性.在未来的研究中，可以进一步对于自然边界条件下的生灭过程的三类拟平稳分布的吸引域问题展开研究.