改进蝴蝶优化算法在QAR数据重构中的应用

张 鹏，刘赟跃，段照斌

(中国民航大学a.适航学院；b.电子信息与自动化学院；c.工程技术训练中心，天津 300300)

快速存取记录器（QAR，quick access recorder）作为飞机飞行数据记录设备，记录了整个飞行过程中飞机各系统的运行状态、飞行姿态及飞行员操作等数据，完整地反映了飞机的实际飞行状态。利用QAR数据可以进行飞机飞行品质监控、故障诊断、飞行事故分析等。由于QAR数据中记录的参数来自飞机上各传感器测量的原始参数，含有一定的噪声及误差，尤其是飞行姿态参数，所含误差会导致飞行姿态QAR数据间不相容，即其数据间不满足运动方程组，从而不利于QAR数据的分析与使用。因此，需要根据QAR数据中飞行姿态参数的冗余信息对飞行姿态QAR数据进行修正和重构，才能准确地反映飞机的飞行姿态。

飞行数据重构的常用方法是利用最小二乘法、极大似然估计法及卡尔曼滤波法对测量系统误差参数进行辨识与估计[1]，然后根据辨识出的误差参数对飞行数据进行修正与重构。但最小二乘法和卡尔曼滤波法适用于线性系统[2-3]，极大似然估计法计算复杂且所用的基于梯度迭代求解算法易陷入局部最优而难以得到全局最优解。

智能优化算法不依赖于问题本身模型的特性，能够快速有效地搜索复杂、高度非线性的多维空间，具有全局性、并行性、鲁棒性、普适性等优点，非常适合于辨识、估计系统参数[4]。蝴蝶优化算法（BOA，butterfly optimization algorithm）是Arora 等[5]于2018年提出的全局智能优化算法，并通过对比实验证明了该算法相对于其他全局优化算法具有较大优势。为了进一步提高蝴蝶优化算法的性能：文献[6]将Lévy 飞行引入蝴蝶优化算法的两个搜索阶段，加快了算法的局部搜索速度，但Lévy 飞行中重要参数λ的随机生成增加了算法的盲目性；文献[7]采用可变的感觉模态对算法进行优化，在迭代初期使感觉模态c快速增大以便在解空间中大范围搜索，在迭代后期减小c增大的速度使算法能快速收敛到全局最优值，但没考虑对全局搜索和局部搜索有直接影响的转换概率P的优化；文献[8]将蝴蝶优化算法和人工蜂群算法相结合，改善了蝴蝶优化算法的局部搜索能力，在提高算法收敛速度的同时也增加了算法迭代过程的复杂性，不利于其在复杂优化问题中的应用。

综上，针对传统方法的局限性及蝴蝶优化算法迭代过程计算复杂、收敛速度慢等不足，采用一种改进的蝴蝶优化算法对系统误差参数进行辨识与估计。通过引入混沌映射来初始化蝴蝶种群，使之均匀分布在解空间上以提高初始种群的多样性，并在每次迭代时动态调整转换概率以提高算法的收敛速度，再根据最小二乘准则将系统误差参数估计转化为最小化修正数据残差平方和的优化问题。最后，将该方法应用于QAR数据中飞行姿态角及其角速度的修正与重构，通过实验验证了该方法的有效性。

1 蝴蝶优化算法

蝴蝶优化算法模仿自然界中蝴蝶的觅食行为，假设每只蝴蝶都能发出一定强度的香味，且都能感知周围其他蝴蝶发出的香味，蝴蝶所发出的香味强度与其位置的适应度值有关，这样蝴蝶之间就可以通过香味来相互吸引、分享信息。同时，每只蝴蝶都能随机地移动或朝着散发香味更强的蝴蝶移动，以此来改变自己的适应度值。

该算法中蝴蝶感知到的香味强度f是关于刺激强度I的函数，其关系可表示为

式中：c为感觉模态；a为香味强度衰减指数；刺激强度I的大小与目标函数或适应度值有关。

蝴蝶优化算法在初始化阶段定义目标函数和解空间，并对算法中的相关参数赋值，然后在解空间中随机生成一群以位置表示的蝴蝶，并根据目标函数和式（1）计算每只蝴蝶的适应度值和香味强度。

每只蝴蝶在迭代阶段可以随机移动或向全局最优的蝴蝶移动，两种移动分别称为局部搜索和全局搜索，局部搜索与全局搜索阶段的位置更新如下

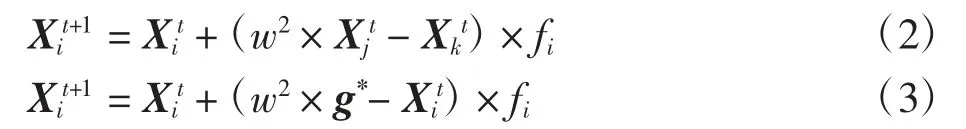
蝴蝶在觅食过程中全局搜索和局部搜索都会发生，同时考虑到现实中随机因素（如雨、风等）对蝴蝶觅食的影响，在BOA 中用转换概率P来模拟现实中的随机因素，用P来决定蝴蝶进行全局搜索还是局部搜索：将每次迭代生成的一个介于区间[0，1]之间的随机数Q与P进行比较，若随机数Q＜P时进行全局搜索，反之则进行局部搜索。

当满足迭代停止条件时，最优蝴蝶位置g*即为全局最优解。

2 蝴蝶优化算法改进

蝴蝶优化算法同其他智能优化算法一样具有易陷入局部最优、收敛速度慢等缺点。通过引入混沌映射对种群进行初始化以及动态调整搜索策略对算法进行改进。

2.1 混沌映射初始化

种群初始化对智能优化算法的收敛性和寻优性能有很大影响。在没有任何先验知识的情况下，解空间的任何一个位置是最优解的概率是相等的，因此，初始种群在解空间中均匀分布及种群多样化更有利于找到全局最优解。

混沌系统具有遍历性、随机性和均匀性的特点，采用混沌初始化可以提高智能优化算法种群的多样性、算法的收敛性及收敛速度[9]。因此，采用混沌初始化来产生蝴蝶种群的初始位置。Logistic 映射是应用最广泛的混沌映射，可以将其应用于蝴蝶种群的初始化，但Logistic 映射由于特定的初始值会导致混沌序列最终收敛于固定值，可能对种群的多样性产生不利影响。因此，采用改进的Logistic 映射[10]对蝴蝶种群进行初始化，其数学模型可表示为

式中Si，j∈[0，1]为混沌变量，i=1，2，…，M，j=1，2，…，N，M表示种群数量，N表示种群所在解空间的维度。初值S1，j可以在[0，1]区间随机生成，然后将生成的混沌序列映射到解空间，即

式中：Xi，j表示初始种群蝴蝶位置向量X0i中的第j个元素；Xmin，j、Xmax，j分别表示Xi，j可能取的最小值和最大值。

2.2 动态调整搜索策略

在蝴蝶优化算法中转换概率P决定蝴蝶进行局部搜索或全局搜索，当P较大时，蝴蝶主要进行全局搜索，当P较小时，蝴蝶主要进行局部搜索。因此，可随着迭代次数的增加来改变转换概率P的值，使得迭代前期主要进行全局搜索以便快速确定最优解所在大概位置，迭代后期主要进行局部搜索以提高解的精度。因此，转换概率P的动态调整如下

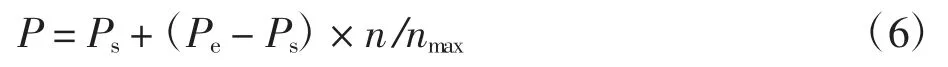
式中：n表示迭代次数；nmax表示最大迭代次数；Ps和Pe分别表示转换概率动态调整的初值和终值。

改进的蝴蝶优化算法流程如图1所示。

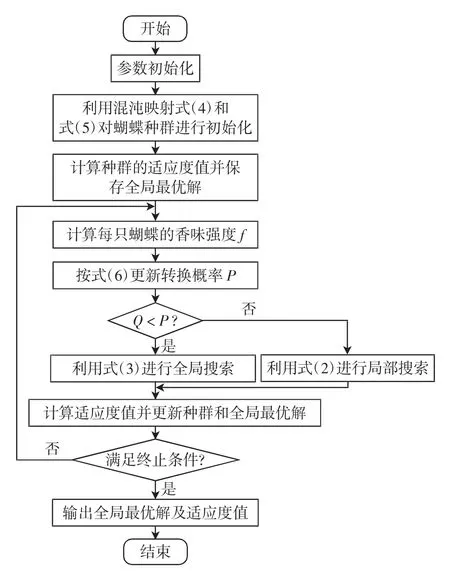
图1 改进的蝴蝶优化算法流程图Fig.1 Flow chart of improved butterfly optimization algorithm

3 系统误差模型

QAR数据中的飞行姿态数据作为传感器测量数据，其误差可分为系统误差和随机误差，系统误差也称为确定性误差，由工作不稳定性和零位漂移引起[1]，主要可以分为比例因子误差和零位偏置误差。传感器的误差模型可表示为

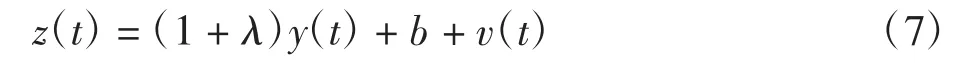
式中：z（t）表示传感器实际测量值；y（t）表示被测量真值；λ为比例因子误差系数；b为零位偏置误差；v（t）为随机测量噪声。

在不考虑随机误差的情况下，传感器实际测量值与被测量真值的关系可用图2 表示（k代表斜率）。

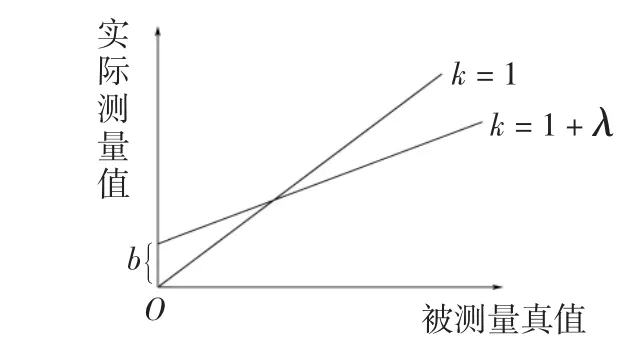
图2 传感器实际测量值与被测量真值的关系Fig.2 The relationship between the measured value and the true value of the sensor

选取QAR数据中的滚转角φ、俯仰角θ、偏航角ψ和机体轴的滚转角速度p、俯仰角速度q、偏航角速度r作为原始数据，利用姿态角和角速度间所满足的运动方程及改进的蝴蝶优化算法对其包含的系统误差参数进行辨识，达到修正、重构姿态角和角速度的目的。

飞机的角运动方程[11-12]如下

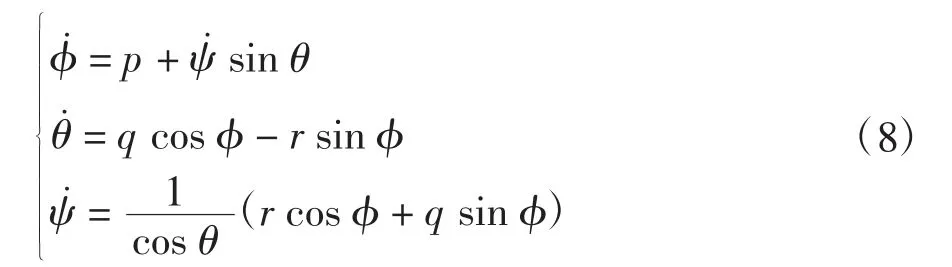
QAR数据中原始的飞行姿态数据φ′，θ′，ψ′，p′，q′，r′的比例因子误差系数表示为λφ，λθ，λψ，λp，λq，λr；零位偏置误差表示为bφ，bθ，bψ，bp，bq，br；被测量真值用φ，θ，ψ，p，q，r表示。若不考虑随机误差可得

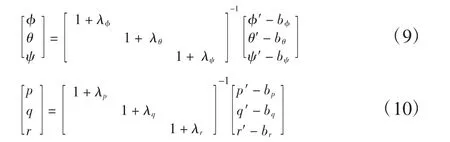
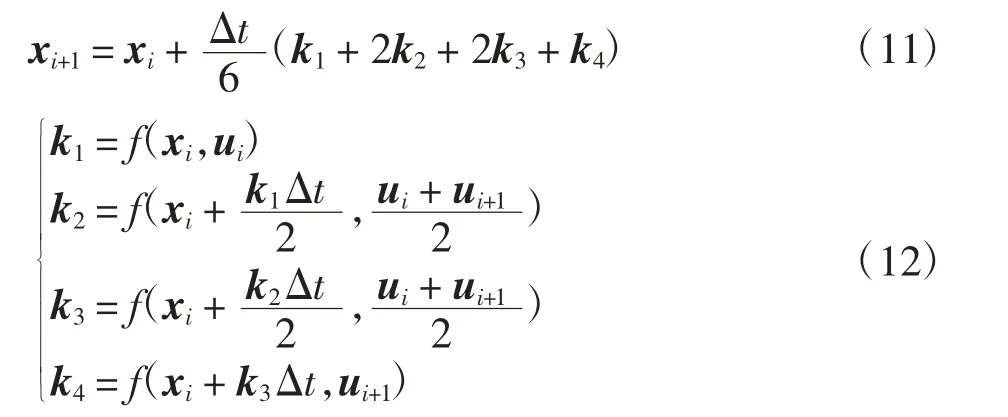
式中Δt为QAR数据的采样间隔。

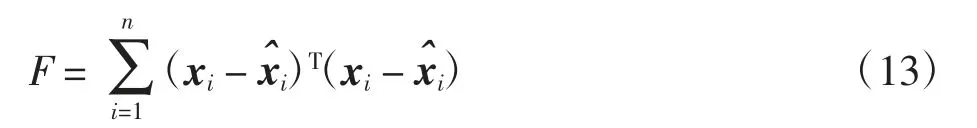
实现对比例因子误差系数和零位偏置误差的估计。

4 实验结果分析

为验证所提方法的有效性，选取某飞机一段长为650 s 的QAR数据作为原始数据，将其分为2 部分：前350 s 用作估计系统误差参数，后300 s 用来对估计的系统误差参数进行有效性验证。飞行姿态角数据和角速度数据之间的相容性可利用姿态角速度经数值积分导出的姿态角与实际姿态角的拟合程度进行评价。

采用决定系数R2及拟合优度指标RNL[13]作为评价拟合程度及相容性指标，其计算公式如下

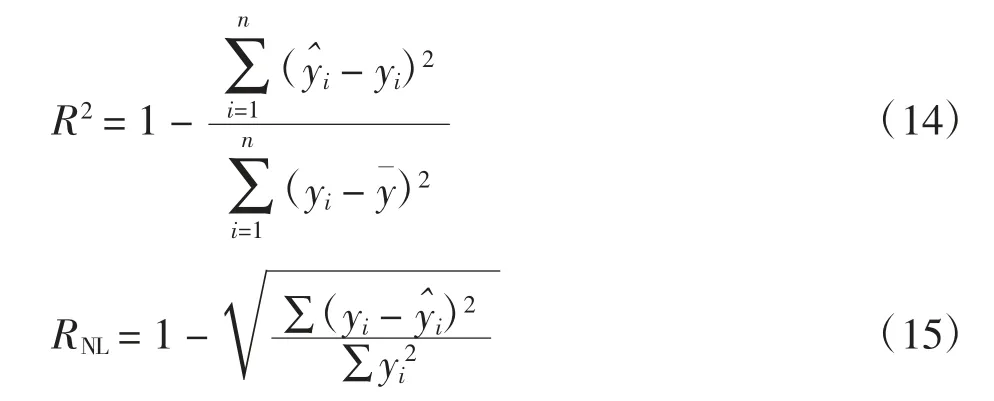
式中：yi为真实值或实际值；为估计值或导出值。R2和RNL的值越接近于1，曲线拟合程度越好[14]，导出姿态角和实际姿态角间的误差越小，数据相容性越高。

图3 是对飞行姿态参数进行重构前绘制的曲线，其中：虚线是直接利用所选QAR数据中第1 s 时的飞行姿态角作为初值，通过式（11）对QAR数据中的姿态角速度直接进行数值积分递推得到的3 个飞行姿态角；实线是QAR数据中相对应的实际飞行姿态角。若QAR数据中的飞行姿态参数不含测量误差，则利用角速度通过数值积分推导出的姿态角应与QAR数据中的姿态角相吻合。但从图3 两条曲线的对比中可以看出：随着时间的推移，QAR数据中实际的飞行姿态角和由角速度导出的姿态角之间的偏差越来越大。其原因是QAR数据中存在的系统误差随着积分运算不断累积进而导致偏差逐渐变大。

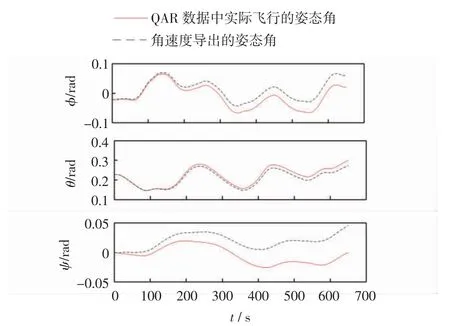
图3 QAR数据中的姿态角及由角速度导出的姿态角Fig.3 Attitude angles in QAR data and those derived from angular velocities

利用改进的蝴蝶优化算法最小化目标函数式（13）可以得到系统误差参数，然后通过式（9）和式（10）即可得到重构后的QAR 飞行姿态数据。

设置改进的蝴蝶优化算法种群数量M=50，最大迭代次数nmax=100，种群所在解空间的维度即系统误差参数个数N=12，系统误差参数的上界和下界分别统一设为0.005 和-0.005。根据测试，当香味衰减指数a=0.1，感觉模态c=0.1，转换概率动态调整的初值Ps和终值Pe分别设为0.8 和0.3 时，蝴蝶优化算法获得最佳寻优性能。

表1 给出了改进前后的蝴蝶优化算法在相同条件下对飞行姿态参数进行10 次重构的拟合指标平均值。由表1 可知，对蝴蝶优化算法进行改进后，在相同的迭代次数下获得了更高的拟合指标，使数据之间的相容性得到了进一步提高，也表明了经过改进的蝴蝶优化算法的性能得到了提升。

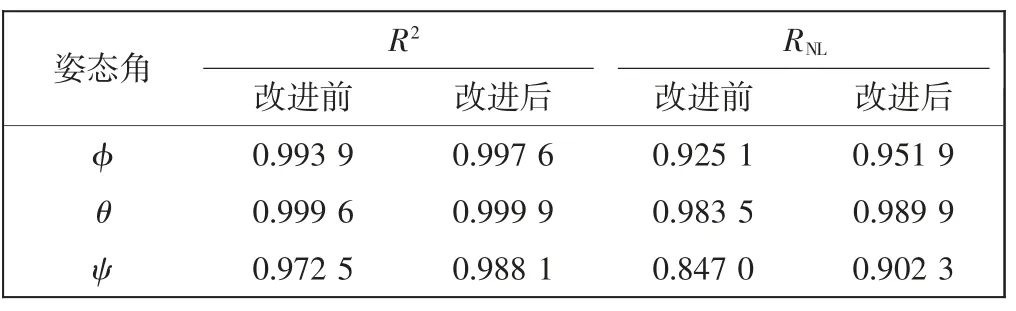
表1 蝴蝶优化算法改进前后拟合指标平均值对比Tab.1 Comparison of the average value of fitting indexes before and after the improvement of BOA

图4 和图5 是利用改进的蝴蝶优化算法对系统误差参数进行估计，得到当系统误差系数[λφ λθ λψ λp λq λr bφ bθ bψ bp bq br]=[0.001 1 0.000 9 -0.001 9-0.002 9 0.002 6 -0.000 8 -0.001 9 0.003 7 0.003 3 0.002 4 -0.001 5 0.003 3]时，QAR数据的姿态角与角速度重构前后的对比曲线。

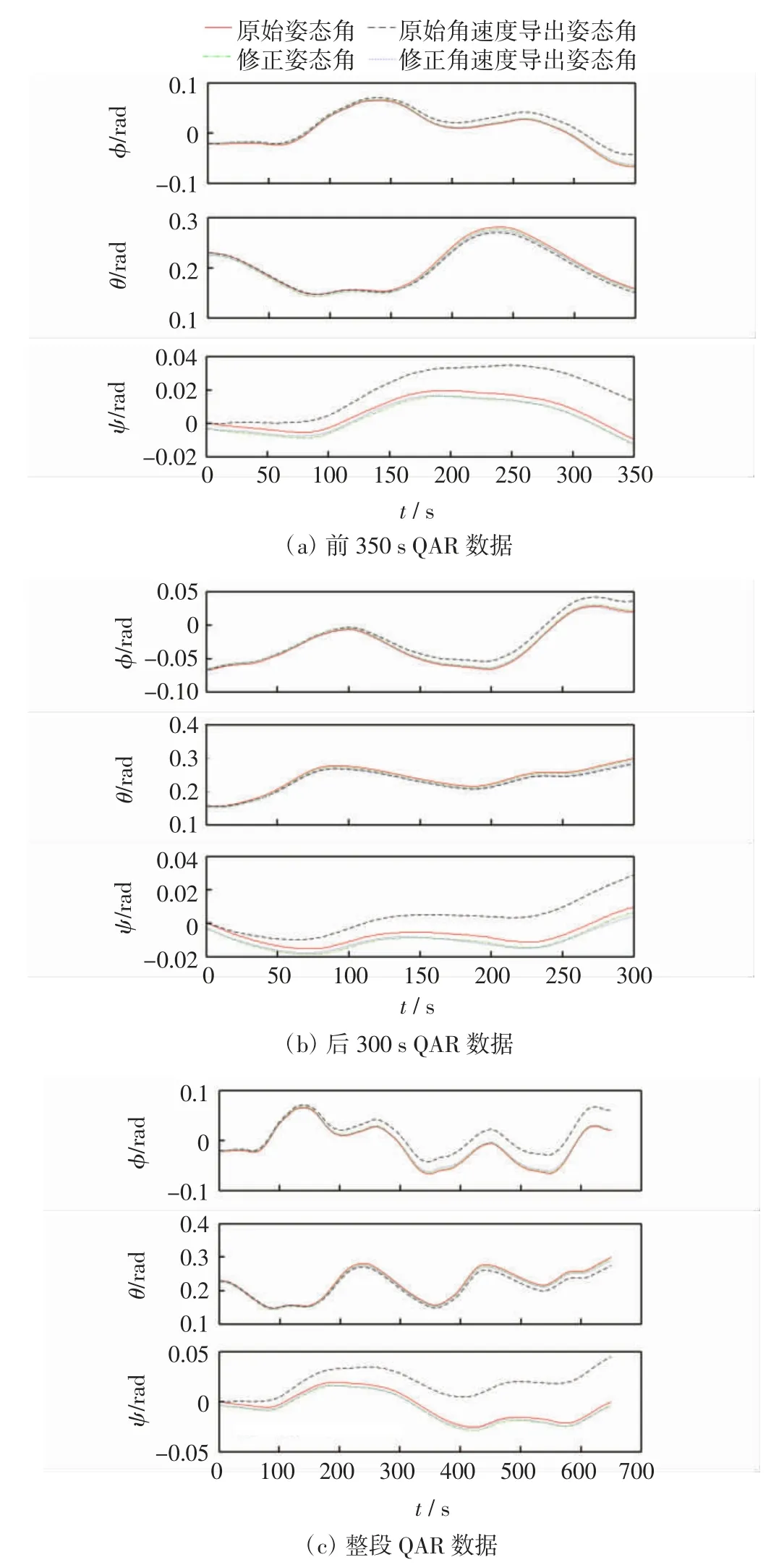
图4 重构前后姿态角间的对比Fig.4 Comparison of attitude angles before and after the reconstruction

对比图4（a）、4（b）、4（c）可直观地得到：利用改进的蝴蝶优化算法对系统误差参数进行估计并用于QAR 飞行姿态角及角速度数据的重构，提高了数据的相容性。图4（b）是利用前350 s 的QAR数据估计得出的系统误差参数对后300 s 的数据进行修正和重构所得的曲线，可以得出利用前段QAR数据估计得出的系统误差参数也同样适用于后段QAR数据的修正，从而验证了所估计系统误差参数的有效性。通过图5中修正的角速度与原始角速度的对比可知，修正后的滚转角速度p和偏航角速度r小于原始值，俯仰角速度q大于原始值，与图3 中角速度导出的滚转角和偏航角大于实际值、导出的俯仰角小于实际值相对应，进一步表明了数据重构结果的合理性。

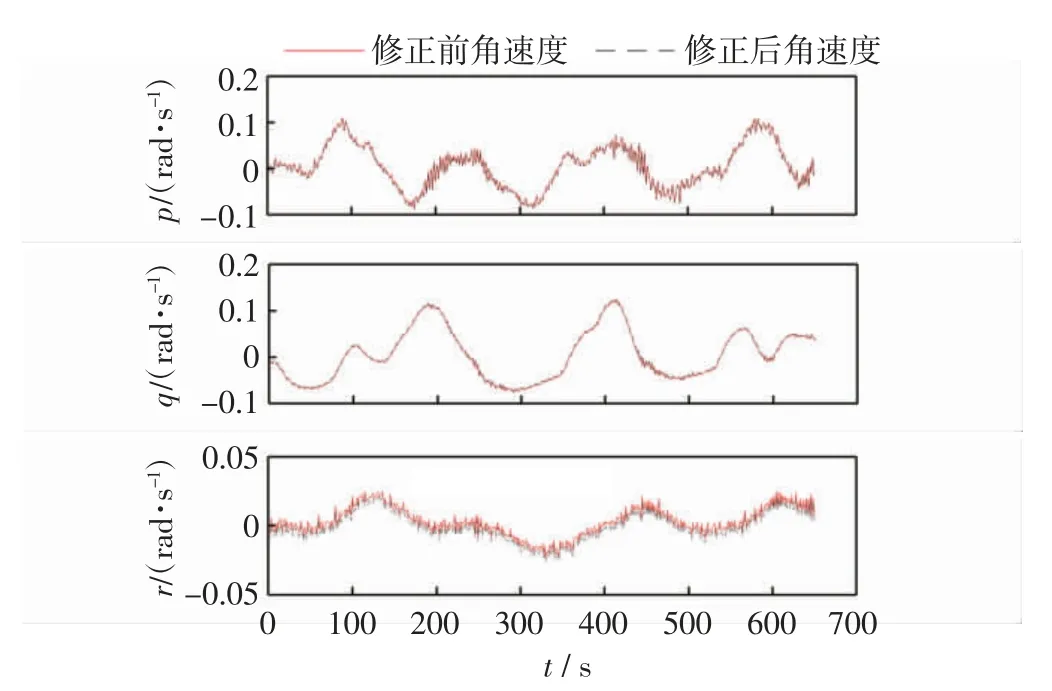
图5 QAR数据重构前后的角速度对比Fig.5 Angular velocities before and after data reconstruction of QAR

表2 分别列出了修正前后姿态角的拟合指标，经过修正和重构后R2及RNL都得到了提高，更接近理想值1，其中，偏航角修正前拟合优度指标因拟合偏差过大而出现负值，修正后达到0.9 以上。

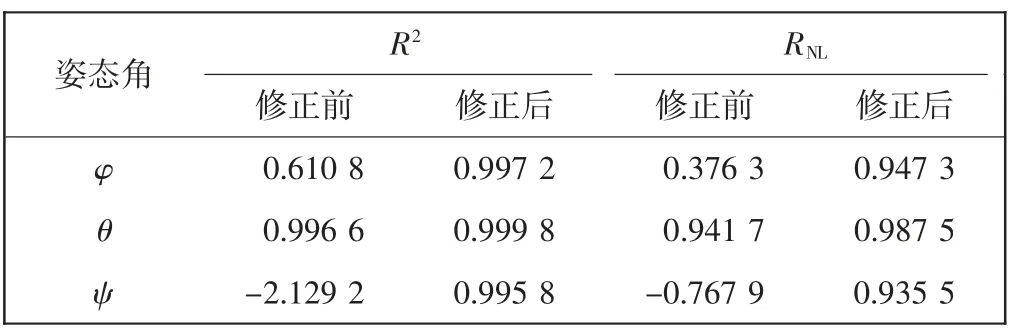
表2 姿态角修正前后拟合指标对比Tab.2 Comparison of fitting indexes before and after correction of attitude angle

5 结语

通过对QAR数据测量误差及蝴蝶优化算法的分析，将改进的Logistic 映射引入蝴蝶优化算法的种群初始化中，并通过动态调整转换概率改进蝴蝶优化算法，然后对QAR数据中姿态角和角速度建立含有系统误差参数的模型，利用改进的蝴蝶优化算法对系统误差参数进行估计进而对QAR数据进行修正和重构，提高了数据间的相容性。实验结果表明，该方法思路清晰、修正精度较高，为QAR数据的修正与重构提供了一种新的思路。