基于椭球模型的超视距时差定位精度分析

王 翔，周 晨，李 江，张冬亮

基于椭球模型的超视距时差定位精度分析

王 翔1，周 晨2，李 江3，张冬亮3

（1. 湖北大学 计算机与信息工程学院，武汉 430062；2. 武汉大学 空间物理系，武汉 430072；3. 中国电子科技集团公司第十研究所，成都 610036）

对流层散射能够实现无线电波的超视距传播。通过目标源信号经过对流层散射到达3个不同探测站的时间差的精确测定，可以实现目标源的高精度定位。为了分析对流层超视距散射三站时差定位精度，给出了基于地球椭球模型的超视距时差定位原理，建立了对流层散射超视距三站时差定位的误差方程，分析了3个不同探测站和散射体位置分布对目标源定位精度的影响。分析结果显示，三站间时差测量误差显著影响定位精度，而三站的站址测量误差和散射体位置误差对超视距定位精度的影响不明显，站站间的基线长度和站型分布对定位精度的分布有显著影响。

对流层散射；椭球模型；超视距探测；三站时差定位；几何精度因子

0 引言

无源目标定位的原理是通过对接收信号的方位、时间、幅度、频率、相位等参数的精确测量，结合相应的信号传输理论，来实现目标源定位。在对目标进行无源定位时，利用多套电子侦察设备对同一辐射源进行探测，可以测量出辐射源目标信号到达任意两个侦察设备之间的时间差，进而形成多组到达时间差双曲线；找到任意两组到达时间差双曲线的交点，就可以得到目标的空间位置；这就是时差定位方法[1-3]。超视距信号时差定位方法，主要是采用空中平台作为中间站或对空中运动目标开展超视距无源定位。利用机载平台作为中间站的超视距雷达信号三站时差定位方法可以对海面目标进行高精度定位[4]。对于超低空目标，也可采用利用空中平台获取超视距目标的信号，利用时差定位方法解析目标点位置[5]。无线电波对流层散射的前向散射波可以被远端处于地平线之下的天线接收，利用对流层散射实现超视距辐射源的定位是一种不主动发射电磁波的被动探测手段，具有隐蔽性好的特点，符合现代战争要求[6]。基于电磁波对流层散射的超视距时差定位方法是一种对地基目标的高精度定位方法，其特点是适合传播的电磁波信号频段较宽，适用对象多，传播机制稳定，一年四季均可利用[7]。文献[8]研究了基于对流层散射的时差定位算法。文献[9]基于对流层散射原理，提出了基于球面的超视距时差定位技术，讨论了3个探测站位于同一条大圆圆弧上时，不同的时差测量误差和不同的基线长度对目标源定位精度的影响。

本文则是基于地球椭球模型，给出对流层散射超视距时差定位的原理。在1984世界大地坐标系统（world geodetic system 1984，WGS-84）定义的地球椭球模型中，给出了对流层散射超视距三站时差定位的定位精度分析。

1 地球椭球WGS-84模型

大地坐标与直角坐标的转换关系[10]为

式中：(,,)为直角坐标系中的坐标；、和分别为大地经度、大地纬度和大地高；为椭球的第一偏心率。另外，的计算公式为

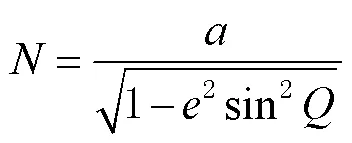
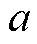
显然，直角坐标满足

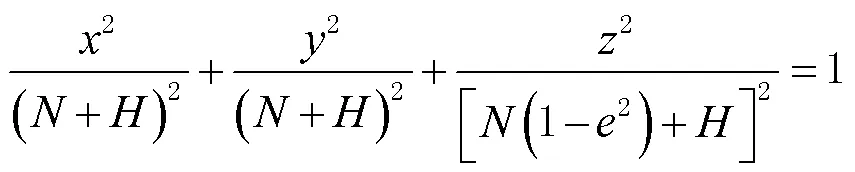
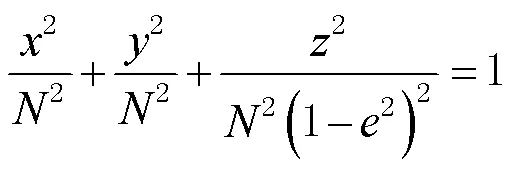
式（4）就是定位方程组中所需要满足的地球椭球面约束条件。

2 地基超视距无源时差定位原理

在对流层散射模型中，接收站收到的信号是经过对流层散射形成多个不同路线传输的信号，在接收端互相叠加而形成的[6-7]。对于位置固定的接收机，其所接收到的信号都是由公共散射体内的多个散射单点散射信号的矢量叠加，不同位置的接收机所收到的信号时差不仅由公共体积内的有效散射体的数量决定，还取决于接收信号矢量叠加时的加权系数[6-7]。对于公共体积内的有效散射体数量，由于对流层的介电特性取决于大气的温度、湿度和压力；随着高度的增高，大气温度和压力逐渐减小，不同高度处的折射指数不同[12]，因此对流层内散射体的分布呈现垂直变化趋势，靠近地面区域的有效散射体分布密度最大。对于接收信号矢量叠加的加权系数的确定要考虑散射体的位置，散射体位置越高，信号传输路径的散射角越大，而散射信道的传输损耗与散射角的3次方成正比，因此高度越高的散射体在接收信号矢量中的贡献越小。综上所述，可以假设等效散射点都靠近公共散射体的底部。

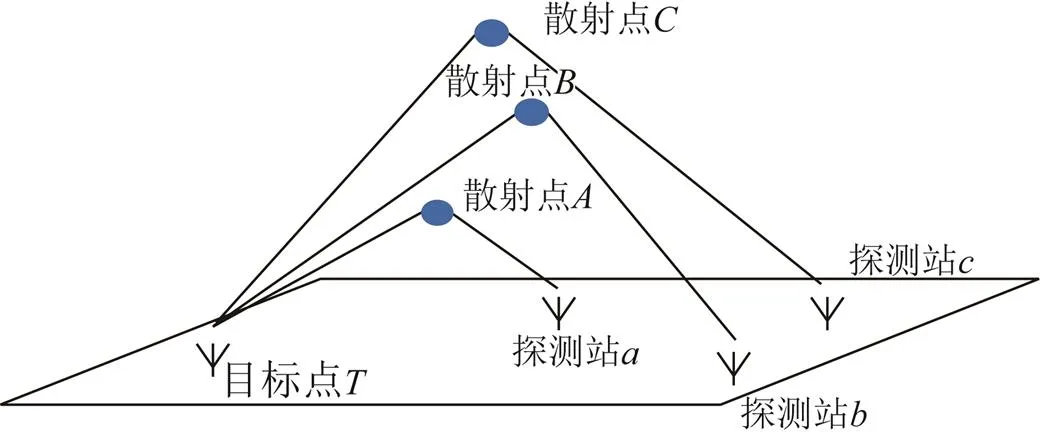
图1 基于对流层散射的超视距时差定位模型

根据时差定位原理，考虑目标点经等效散射体到探测站的传输路径，可以得到基于对流层散射的超视距三站时差定位方程[8]为

3 对流层超视距无源定位误差分析

本文采用几何精度因子（geometric dilution of precision, GDOP）来描述目标点定位误差的几何分布。下面对求解GDOP展开分析。对方程组式（5）求微分，并写成矢量矩阵形式为

式中：

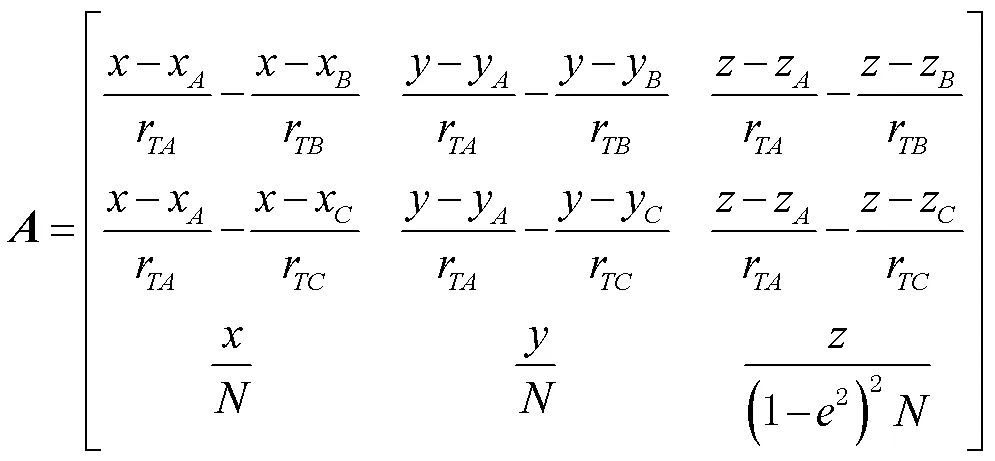
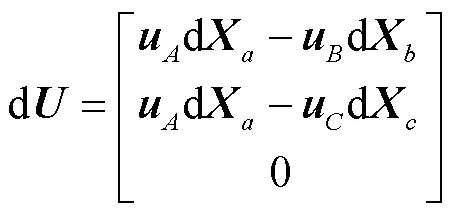
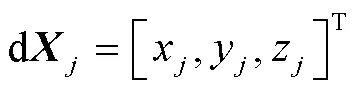
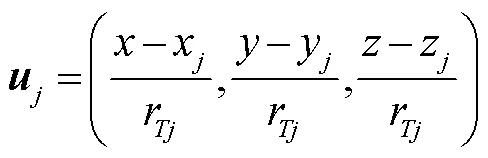
求解式（6）可得

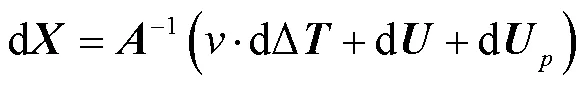
从式（7）中可以看出，目标点定位误差与到达时差测量误差、探测站位置测量误差和散射体位置测量误差成线性关系。

因为各个探测站之间的到达时间差测量是相互独立的，时差测量误差之间互不相关，所以可以假定到达时间差测量误差经过系统误差修正后均值为0。同样地，可以假设探测站站址误差各个分量之间以及各探测站站址误差之间互不相关，散射体位置测量误差各分量之间以及各散射体位置测量误差之间互不相关，且到达时间差测量误差、探测站站址误差以及散射体位置测量误差之间互不相关，那么目标定位误差的协方差就可写为

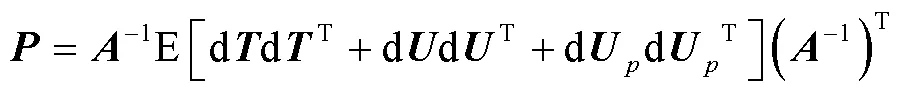
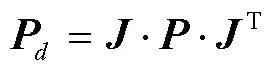
式中：

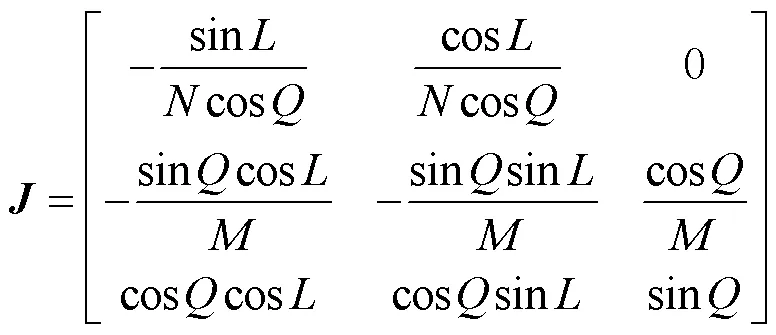
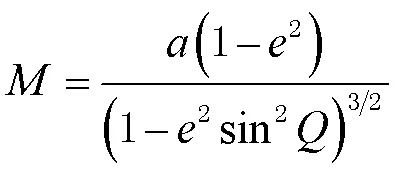
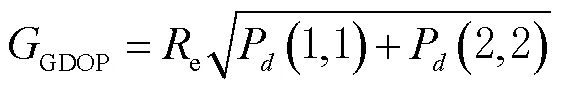
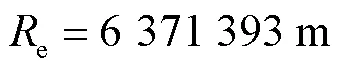
4 GDOP计算结果

根据前文对定位误差几何分布的分析，本文对基于WGS-84模型的对流层散射超视距三站时差定位的定位误差几何分布进行仿真计算。

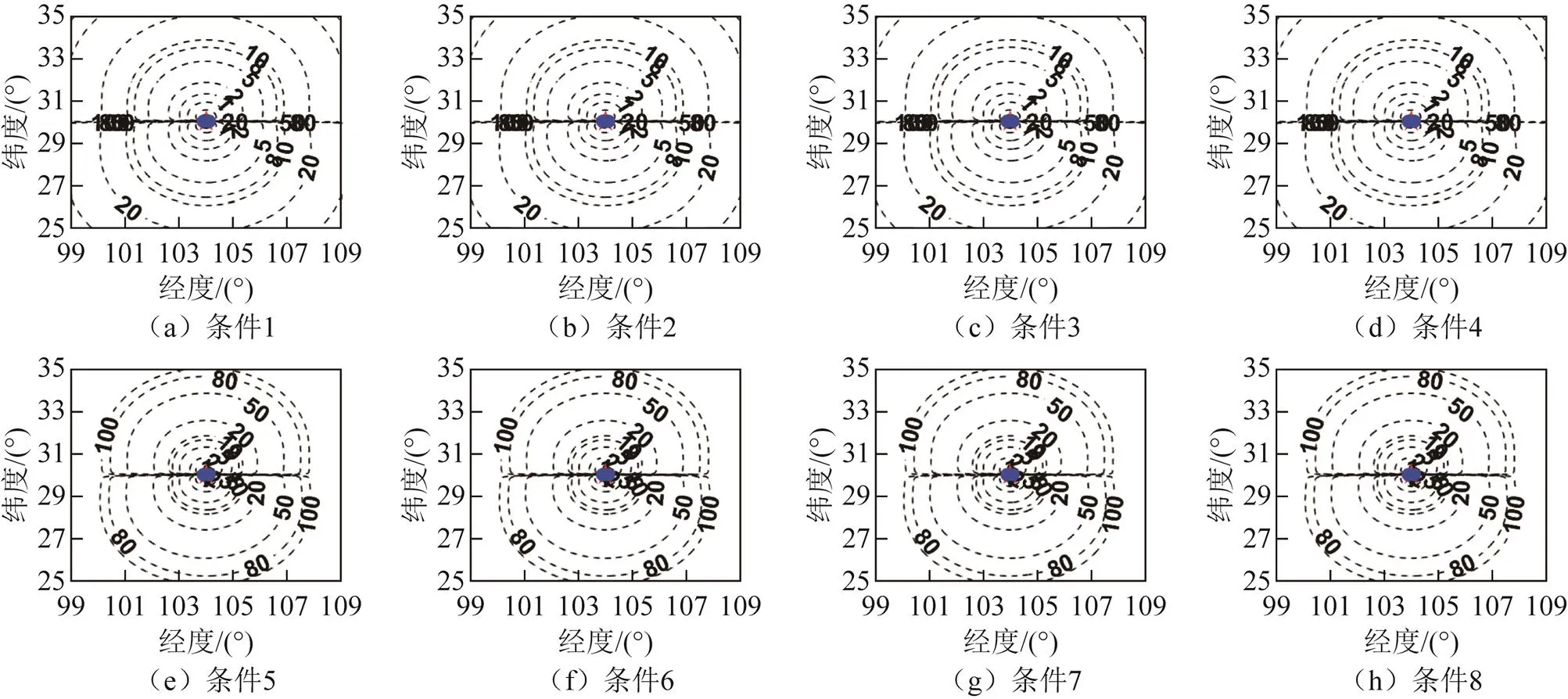
图2 基线长度约为10 km的直线型布站定位精度几何分布

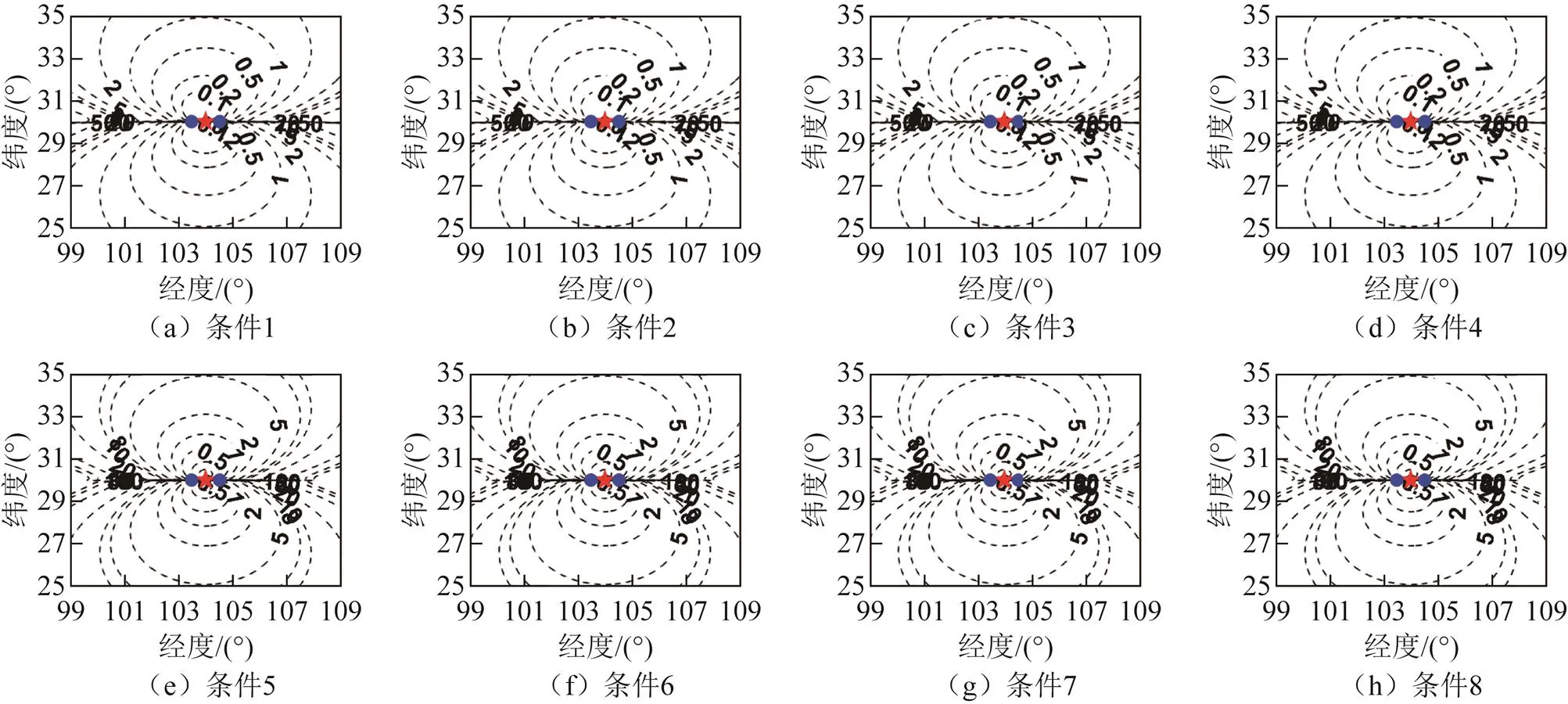
图3 基线长度约为50 km的直线型布站定位精度几何分布

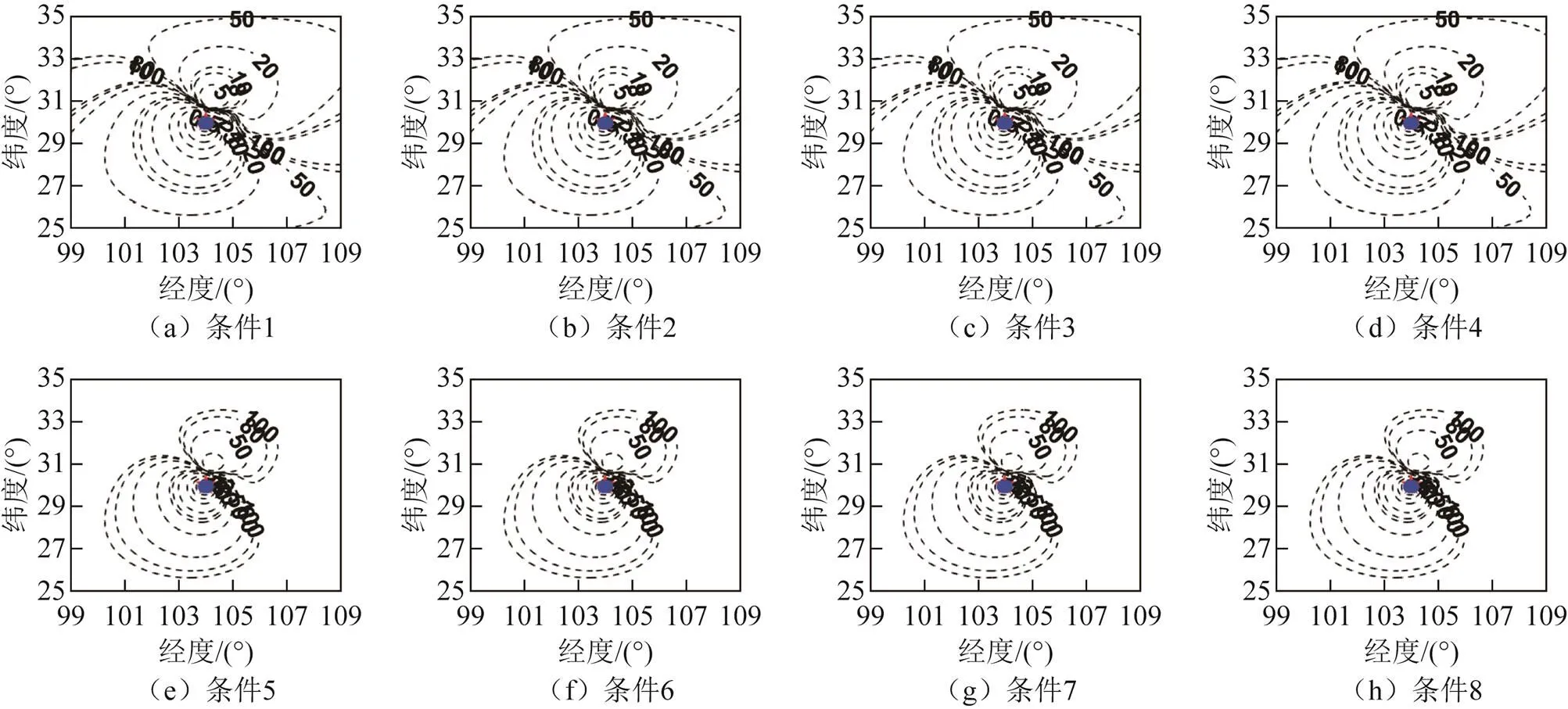
图4 基线长度约为10 km的正三角形布站定位精度几何分布

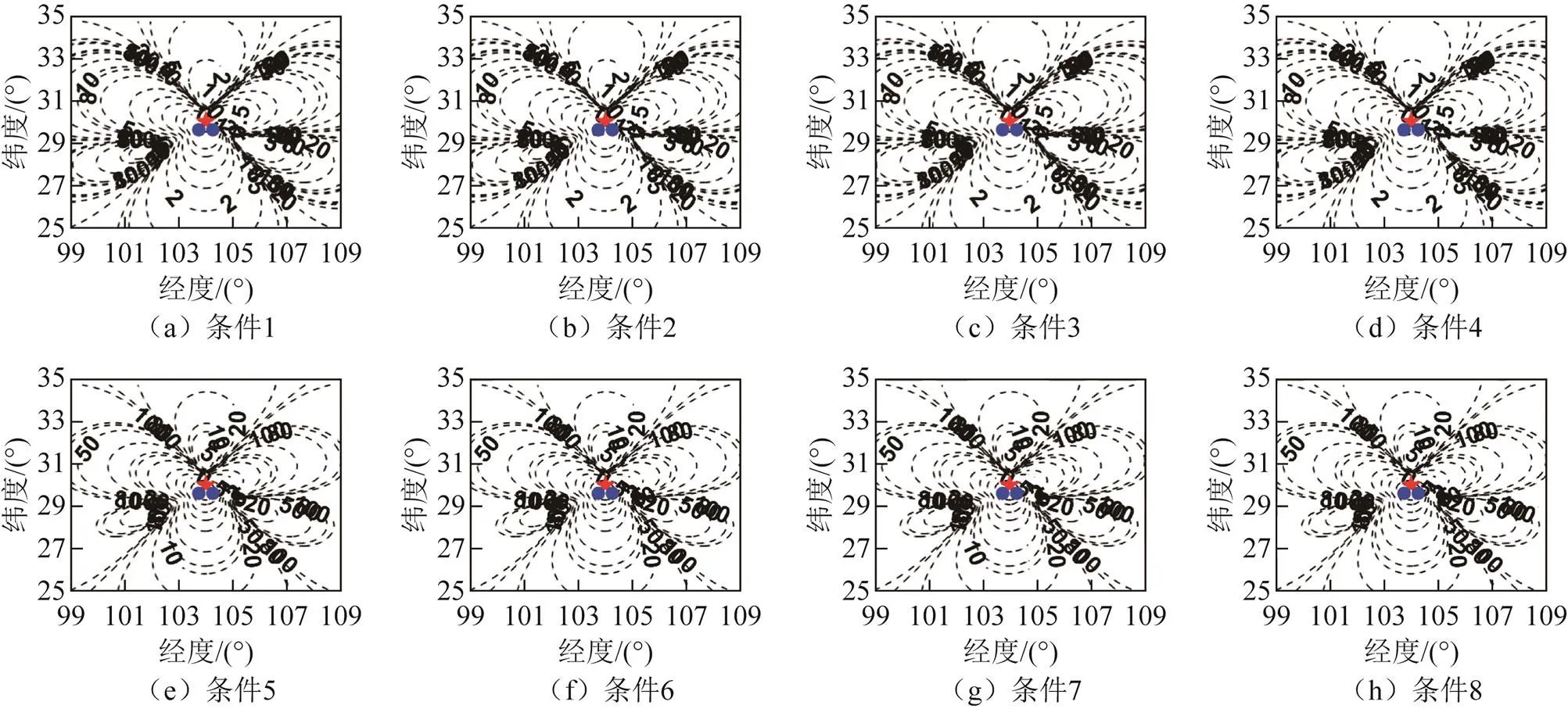
图5 基线长度约为50 km的正三角形布站定位精度几何分布

从图2中可以看出，时差测量误差对定位精度有明显影响，时差测量误差较小时定位精度较高（图2（a）和图2（e））；探测站站址测量误差和散射体位置测量误差对定位精度影响不明显（图2（a）至图2（d））。从图2中还可以看到，基站连线上的定位精度比较差，可能存在定位盲区。

对比图2（a）和图3（a）可以看出，探测站间的基线长度会显著影响定位精度，较长基线情况下有更高的定位精度。对比图2（a）和图4（a）可以看到，不同的探测站位置分布对定位精度的分布有明显的影响，正三角形布站构型会带来更复杂的定位精度分布，且定位精度与直线布站构型相比偏低。图5的长基线正三角形布站构型情况下，3个探测站所包围区域内的定位精度明显高于其他地区，但是也能看出两站连线上的定位精度较差。

5 结束语

根据本文的仿真结果，可以看出基于WGS-84模型的对流层散射超视距三站时差定位方法的定位精度有以下特点：①时差测量误差对定位精度影响较大，时差测量误差越小，定位精度越高；②探测站站址误差和散射体位置误差对定位精度影响不明显；③探测站之间的距离，即基线长度，对定位误差影响明显，随着基线长度的增加，定位精度明显提高；④探测站布站形式对定位精度分布有明显影响；⑤探测站连线上的定位精度较差。

基于对流层散射的无线电波超视距传播，具有单跳距离远、可用频段多、信道可靠性强、抗干扰抗截获能力强等特点，对于实现非合作目标源的无源定位有着良好的应用前景。利用地基超视距接收站可实现对地基、海基、空基等平台的非合作目标源的定位。本文的研究结果显示对流层散射体定位误差对定位精度没有明显影响；提高时差测量误差、探测站位置分布合理对于实现高精度无源定位有着显著的效果。

[1] SMITH W W, STEFFES P G. Time delay techniques for satellite interference location system[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 224-231.

[2] 刘丹军. 到达时间差与多普勒频率差联合定位方法研究[D]. 西安: 西安电子科技大学, 2010.

[3] 郭引川, 翁芸, 杨万全. 无源探测定位技术分析[J]. 现代电子技术, 2004, 27(21): 9-11.

[4] 王钢, 贾世楼, 张琦. 超视距目标指示的方法与性能研究[J]. 哈尔滨理工大学学报, 2006, 11(6):110-113.

[5] 徐丹, 刘以安, 刘同明. 低空超视距目标的无源定位技术研究[J]. 现代雷达, 2007, 29(8): 22-25.

[6] 李志勇, 秦建存, 梁进波. 对流层散射通信工程[M]. 北京: 电子工业出版社, 2017.

[7] 张明高. 对流层散射传播[M]. 北京: 电子工业出版社, 2004.

[8] 卿浩博, 徐汉林, 甘建超, 等. 一种基于WGS_84地球模型的地基超视距时差定位算法[J]. 电子信息对抗技术, 2020, 35(3): 24-28.

[9] 王智显, 徐汉林, 敖庆. 基于对流层散射传播的超视距时差定位[J]. 电子信息对抗技术, 2008, 23(5):18-21.

[10] 王威, 于志坚. 航天器轨道确定:模型与算法[M]. 北京: 国防工业出版社, 2007.

[11] 朱华统, 杨元喜, 吕志平. GPS坐标系统的变换[M]. 北京: 测绘出版社, 1994.

[12] HOINKA K P. Temperature, humidity, and wind at the global tropopause[J]. Monthly Weather Review, 1999, 127(10):2248-2265.

[13] 边少锋, 李文魁. 卫星导航系统概论[M]. 北京: 电子工业出版社, 2005.

Positioning accuracy analysis of the over-the-horizon TDOA based on ellipsoid model

WANG Xiang1, ZHOU Chen2, LI Jiang3, ZHANG Dongliang3

（1. School of Computer and Information Engineering, Hubei University, Wuhan 430062, China; 2. Department of Space Physics, Wuhan University, Wuhan 430072, China; 3. China Electronics Technology Group Corporation No. 10 Research Institute, Chengdu 610036, China）

Troposcatter supports the over-the-horizon propagation of the radio waves. Three detecting stations can passively measure the Time Difference of Arrival (TDOA) of the scattered signal by the troposphere from the target station. Based on WGS-84 model, the three stations TDOA can accurately position the target signal. The purpose of this paper is analysis of positioning accuracy by the troposcatter over-the-horizon three-station TDOA in ellipsoid model. In this paper, positioning equations of the three-station TDOA with WGS-84 are analyzed. Geometric Dilution of Precision (GDOP) are calculated and presented. The GDOP results demonstrate that the measurement tolerance of time significantly affects GDOP, whereas the measurement tolerance of station positions and scatters position do not considerably influence the GDOP. The distance of the detecting stations and the topology of the three stations fairly impact on the topology of the GDOP.

troposcatter; ellipsoid model; over-the-horizon detection; three-station time difference of arrival; geometric dilution of precision

P228

A

2095-4999(2021)06-0071-06

王翔，周晨，李江，等. 基于椭球模型的超视距时差定位精度分析[J]. 导航定位学报, 2021, 9(6): 71-76.（WANG Xiang, ZHOU Chen, LI Jiang, et al. Positioning accuracy analysis of the over-the-horizon TDOA based on ellipsoid model[J]. Journal of Navigation and Positioning, 2021, 9(6): 71-76.）

10.16547/j.cnki.10-1096.20210611.

2021-01-25

国家自然科学基金项目（41704155）；中国博士后科学基金项目（2017M622504，2019T120679）。

王翔（1983—），女，湖南双峰人，博士，副研究员，研究方向为无源定位。

周晨（1983—），男，湖北荆州人，博士，教授，研究方向为电波传播应用、GNSS应用等。