一种矩阵排序改进的模糊度解算方法

田晨冬，李克昭,2

一种矩阵排序改进的模糊度解算方法

田晨冬1，李克昭1,2

（.1. 河南理工大学 测绘与国土信息工程学院，河南 焦作 454000；2. 北斗导航应用技术协同创新中心，郑州 450052）

针对目前应用最为广泛的最小二乘降相关平差（LAMBDA）算法涉及大量矩阵运算，延长了降相关时间的问题，提出一种矩阵排序法（MOM），来提高降相关效率。仿真实验和实测结果表明：在保持与LAMBDA算法精度相当的情况下，MOM方法可将平均解算时间从43690 μs 降低到40970 μs。

模糊度解算；全球卫星导航系统；矩阵排序；最小二乘降相关平差算法；去相关算法

0 引言

在全球卫星导航系统（global navigation satellite system，GNSS）高精度差分定位中，如何准确高效地求解整周模糊度是一项关键问题，因为只有模糊度得到固定，卫星定位才能得到毫米级的定位精度。模糊度处理方法主要包括3类[1]：①坐标域中确定模糊度的方法；②观测值域模糊度解算方法；③模糊度域中确定模糊度的方法。目前以基于整数最小二乘原则，在模糊度域中确定模糊度的最小二乘降相关平差（least-square ambiguity decorrelation adjustment，LAMBDA）算法[2-3]应用最为广泛。LAMBDA解算模糊主要包括3个步骤：首先，通过对整数最小二乘估计获得模糊度的浮点解和相应的协方差矩阵进行降相关处理从而获得固定解；然后，构建模糊度候选区间搜索最优模糊度；最后，对模糊度的准确性进行检验确认。由于其降相关处理涉及大量矩阵运算，延长了降相关时间。因此有必要对其降相关过程进行研究，提高降相关效率。

国内外学者都对降相关过程进行了大量的研究。文献[4]通过上下三角过程构造联合去相关算法，降低了模糊度之间的相关性；文献[5]使用乔列斯基（Cholesky）分解，构建整数高斯矩阵，在高维情况下，分解得到的浮点解协方差矩阵条件数最小；文献[6]以降低协方差矩阵的条件数为准则，提出一种性能更加优越的模糊度去相关算法。自文献[7]将格理论中的规约算法伦斯特拉-伦斯特拉-洛瓦斯（Lenstra-Lenstra-Lovász, LLL）算法应用于模糊度降相关以来，很多学者从格基规约理论角度，分析LLL的降相关性能，文献[8]提出一种逆整数Cholesky去相关方法，其性能优于整数高斯去相关和LLL算法；文献[9]基于分块格拉姆-施密特（Gram-Schmidt）正交化算法，来改进LLL算法，在改善平均相关系数和条件数的基础上，极大地优化了搜索所需的时间；文献[10]采用分块降维，来改进LLL算法，有效地提高了LLL算法的运行效率。

此外有学者研究表明，排序可以优化模糊度去相关算法，提高浮点解方差-协方差矩阵去相关效率[11-13]。文献[14]将基于排序的QR分解策略改进，并应用到LAMBDA算法中，通过贪婪选择和惰性变换，对参数进行去相关，有效地提高了LAMBDA算法的效率；文献[15]将自然升序法、对称旋转法及扰动升序法并行计算，获得了更好的降相关结果。

因此，针对LAMBDA算法降相关过程复杂耗时，排序法可以优化降相关效率的问题，本文基于矩阵排序，对LAMBDA算法的去相关过程进行改进，提出一种Cholesky分解的并行算法即矩阵排序法（matrix ordering method，MOM），并结合仿真实验及实测数据与LAMBDA方法进行对比分析。

1 双差模糊度解算模型

1.1 模糊度最小二乘估计模型

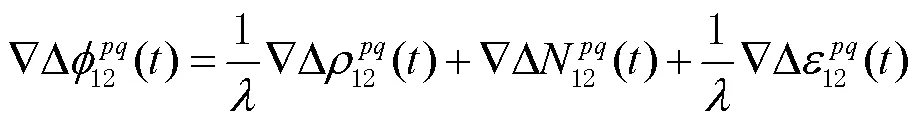
对观测方程式（1）中未知参数进行线性化，并将这些线性化方程集合成一个线性方程组，即

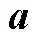
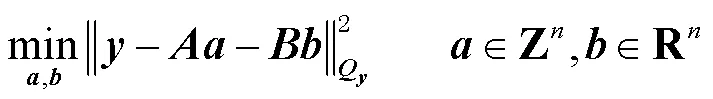
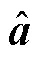
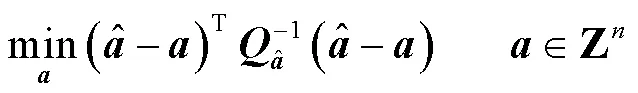
1.2 模糊度降相关

通常模糊度分量之间具有很高的相关性，导致搜索效率低，为了使求解过程更加高效，可以通过整数高斯变换（变换）将最小二乘问题式（4）转化为新的最小二乘问题，其计算方法为

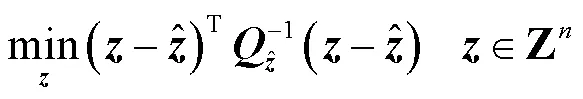
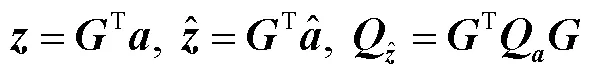
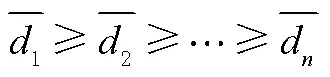
2 改进矩阵排序求解整周模糊度

在模糊度解算过程中，为了满足不等式式（10）需要进行排列计算，由排列引起的计算量直接决定着整个模糊度解算过程的耗时，排列的数量越少模糊度解算越快。因此，本节通过对模糊度排列计算的分析研究提出一种Cholesky分解的并行算法，即MOM算法。

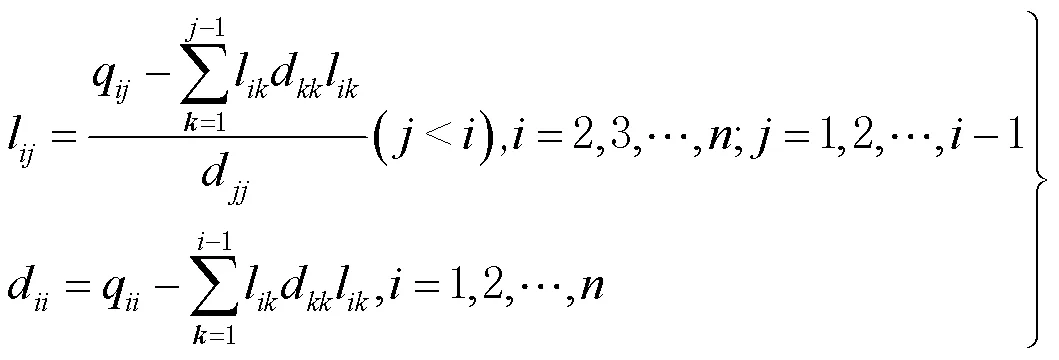
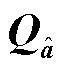
从而提高模糊度解算方法的效率。

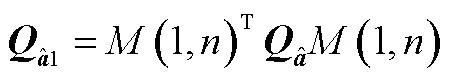
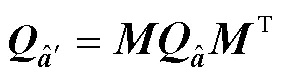
其中

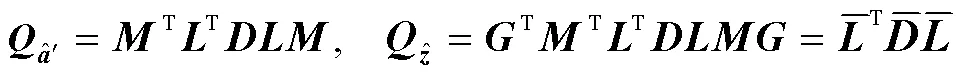
3 实验验证分析

解算精度与时间效率是对一个模糊度解算方法优劣的直接判断，因此本文采用仿真数据与实测数据对MOM算法与LAMBDA算法的解算精度与解算时间进行对比。

MOM算法解算整周模糊度流程图如图1所示。

图1 MOM算法流程图

3.1 仿真实验分析

仿真实验分为2种不同的情况。浮点解向量的构建，采用的函数为

情况2：=diag(200, 200, 200, 0.1, 0.1,…, 0.1)。

从仿真结果可以看出，MOM算法的运行时间普遍优于LAMBDA算法。在低维情况下，2种算法平均运行时间大致相同，但是当维数增大时MOM算法的运行时间相较于LAMBDA算法会越来越短。需要说明的是，在仿真实验中，LAMBDA算法与MOM算法都针对于相同的整数最小二乘问题给出相同的计算解决方法。因此，对于仿真实验所针对的问题，2种算法在准确性方面没有差异。

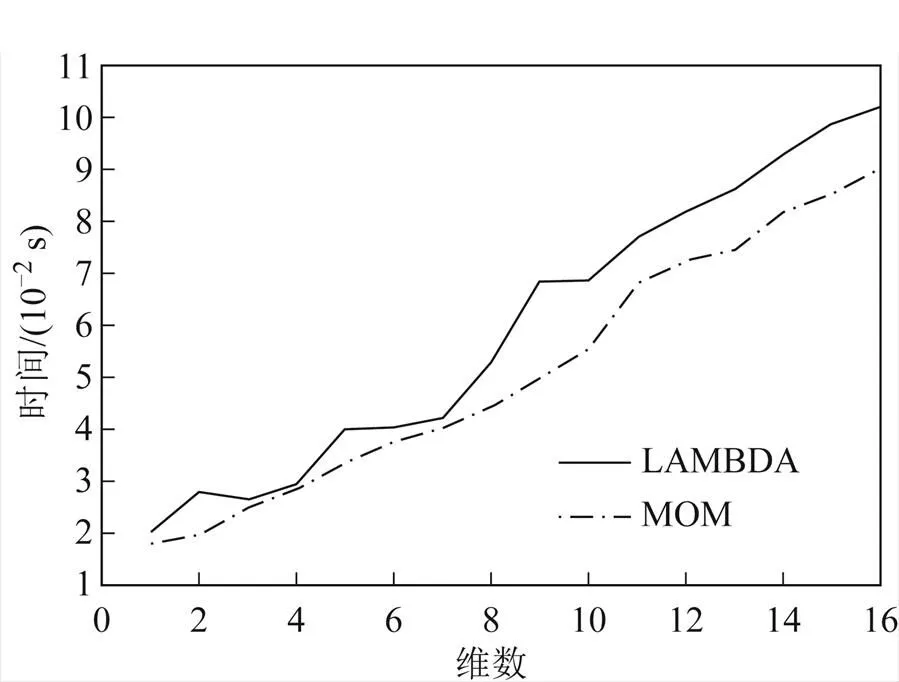
图2 情况1平均运行时间

图3 情况2平均运行时间

3.2 实测实验分析

实测实验采用一组和芯星通UB4B0-MINI板卡采集的静态观测数据。基线长89.83 m，采样间隔1 s，截取了1000个历元进行对解算时间和解算结果进行实验分析。基于Microsoft Visual Studio 2019利用C语言进行了程序设计，所使用的数据为标准接收机自主交换格式（receiver independent exchange format, RINEX）数据，其中包括星历数据和观测数据。

图4展示了一个历元2种方法求解的12维固定解与浮点解对比，特别地，为了便于展示结果小数点前只保留了一位。LAMBDA算法与MOM算法解算模糊度时间如图5所示。表1展示了2种算法解算的最小值、最大值、平均数、标准方差和极差，时间单位为μs。

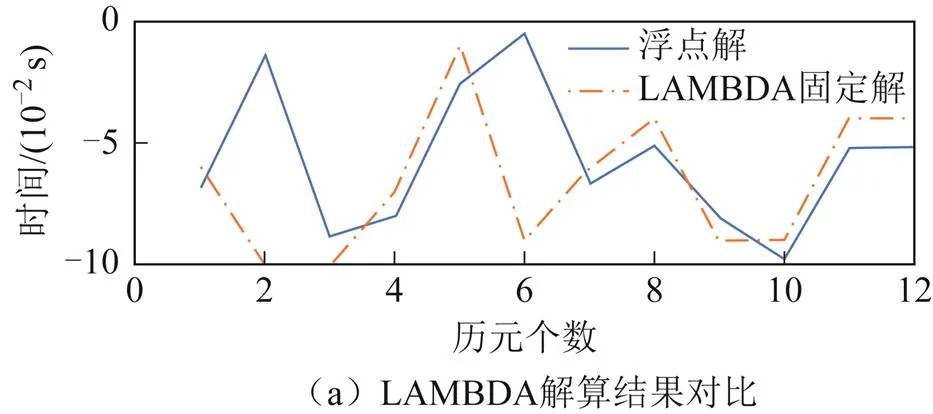
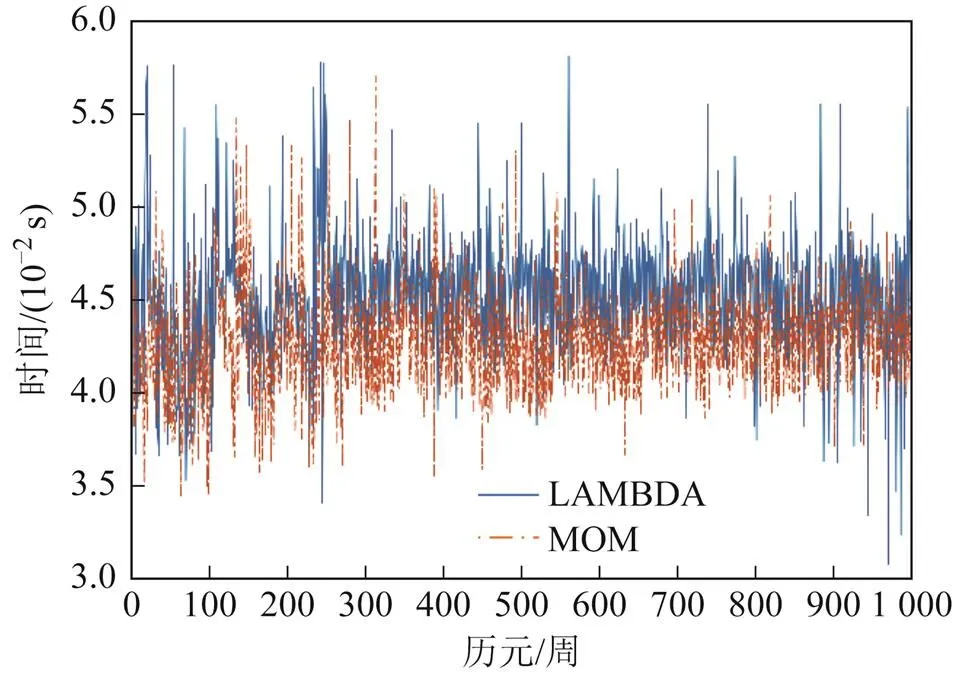
图5 解算时间曲线

表1 解算时间结果 单位：μs

通过图4浮点解与LAMBDA固定解和MOM固定解的结果对比，可以看出MOM算法与LAMBDA算法所解算出的模糊度固定解结果基本一致。因此，MOM算法保证了模糊度固定解的精度，可以满足高精度定位要求。图5清晰直观地表明了MOM算法的有效性。表1的各项数值更验证了MOM算法在解算时间上的优势，其中标准方差为固定解随机变量与其平均值之间的偏离程度，极差代表固定解最大值与最小值之间的差距。从表1中可以看出：相较于LAMBDA算法，MOM算法将模糊度的平均解算时间从43690 μs降低到了40970 μs，标准方差从4590 μs降低到了3323 μs，极差从22350 μs降低到了16420 μs。结合图5和表1分析可以得到：MOM算法解算时间相比于LAMBDA算法短且稳定性更好。

综上所述，本文提出的MOM算法可以在保证模糊度固定解精度不变的情况下降低模糊度固定解的解算时间。通过仿真与实测数据实验进一步验证了该结论。

4 结束语

本文分析了GNSS载波相位双差模糊度解算模型，针对模糊度去相关过程，引入矩阵排序法，提出一种基于Cholesky分解的MOM并行算法，并进行了仿真分析与实测数据实验验证。仿真与实测实验结果表明：MOM算法求解模糊度在精度上与LAMBDA算法一致，但其搜索时间效率与稳定性高于LAMBDA算法。

如何对矩阵排序法改进以提高模糊度搜索效率、提升搜索准确性是今后需要进一步研究的问题。

[1] 李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.

[2] TEUNISSEN P J G. The least-square ambiguity decorrelation adjustment: a method for fast GPS ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1/2): 65-82.

[3] TEUNISSEN P J G. The invertible GPS ambiguity transformations[J]. Manuscript Geodesy, 1995, 20 (6):489-497.

[4] LIU L T, HSU H T, ZHU Y Z, et al. A new approach to GPS ambiguity decorrelation[J]. Journal of Geodesy, 1999, 73(9): 478-490.

[5] XU P. Random simulation and GPS decorrelation[J]. Journal of Geodesy, 2001, 75(7/8): 408-423.

[6] 陈树新. GPS整周模糊度动态确定的算法及性能研究[D].西安: 西北工业大学, 2002.

[7] HASSIBI A, BOYD S. Integer parameter estimation in linear models with applications to GPS[J]. IEEE Transactions on Signal Processing,1998,46(11):2938-2952.

[8] XU P. Parallel Cholesky-based reduction for the weighted integer least squares problem[J]. Journal of Geodesy, 2012, 86(1):35-52.

[9] 范龙. 基于格理论的GNSS模糊度估计方法研究[D]. 郑州: 信息工程大学, 2013.

[10] 卢立果. GNSS整数最小二乘模糊度解算理论与方法研究[D]. 武汉: 武汉大学, 2017.

[11] 鲁铁定,汪鑫,卢立果,等. 排序对模糊度解算中降相关性能的影响分析[J]. 大地测量与地球动力学, 2020, 40(5): 470-475.

[12] 苏明坤. GPS/北斗高精度相对定位关键技术研究[D]. 武汉:武汉大学, 2018.

[13] 蒋涅, 裴炳南, 张豪生. 一种改进的整周模糊度去相关算法[J]. 电光与控制, 2020, 27(1): 37-41.

[14] CHANG X W, YANG X, ZHOU T. MLAMBDA: a modified LAMBDA method for integer least-squares estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565.

[15] XU P. Parallel Cholesky-based reduction for the weighted integer least squares problem[J]. Journal of Geodesy, 2012, 86(1): 35-52.

A method of ambiguity resolution based on matrix ordering

TIAN Chendong1, LI Kezhao1,2

（1. School of Surveying and Land Information Engineering, Henan Polytechnic University, Jiaozuo, Henan 454000, China;2. Collaborative Innovation Center of BDS Research Application, Zhengzhou 450052,China）

In view of the fact that the Least-square Ambiguity Decorrelation Adjustment (LAMBDA) algorithm, which should be the most widely used method to determine the ambiguity, involves a lot of matrix operations in its decorrelation processing and prolongs the decorrelation time, this paper proposes a Matrix Ordering Method (MOM), which can improve the efficiency of decorrelation. Compared with the LAMBDA algorithm, simulation experiments and actual measurement results show that the average solution time of MOM algorithm is reduced from 43690 μs to 40970 μs while the accuracy of LAMBDA algorithm remains unchanged.

ambiguity resolution; global navigation satellite system; matrix ordering; least-square ambiguity decorrelation adjustment algorithm; decorrelation algorithm

P228

A

2095-4999(2021)06-0065-06

田晨冬，李克昭. 一种矩阵排序改进的模糊度解算方法[J]. 导航定位学报, 2021, 9(6): 65-70.（TIAN Chendong, LI Kezhao. A method of ambiguity resolution based on matrix ordering[J]. Journal of Navigation and Positioning, 2021, 9(6): 65-70.）

10.16547/j.cnki.10-1096.20210610.

2021-01-20

国家自然科学基金项目（41774039）；国家重点实验室项目（6142210200104）。

田晨冬（1998—），男，河南商丘人，硕士研究生，研究方向为卫星导航与定位技术。

李克昭（1977—），男，甘肃靖远人，博士，教授，研究方向为卫星定位/视觉导航的理论。