基于优化灰色傅里叶残差修正的中长期负荷预测

朱健安，魏云冰，朱鹏杰，蒋成成，朱成名

(1.上海工程技术大学 电子电气工程学院,上海 201620;2.郑州轻工业大学 建筑环境工程学院,河南 郑州 450000)

近年来，随着人民生活质量不断提高和宏观经济的发展，人们对电能的需求也越来越大，很多地区的年度负荷都大幅增长。为了更好地保证电力供需平衡和电网的安全运行，中长期负荷预测显得尤为重要。中长期负荷预测方法研究可分为传统的经典预测算法和现代预测算法[1]。传统的经典预测算法以时间序列分析法为代表，例如回归分析法、趋势外推法、灰色预测法等。文献[2]采用时间序列分析法对负荷进行预测，取得了不错的效果。虽然传统的时间序列法运算量小且运算速度快，但其不具备自适应学习能力，预测误差也比较大。文献[3～5]采用灰色模型进行预测。传统灰色模型对数据数量要求不高，但对数据质量要求比较高，因此对递增式数据预测的效果更好。近年来，随着人工智能技术的兴起，出现了以神经网络、支持向量机、小波分析为主的现代预测算法。文献[6～9]采用神经网络提高了负荷预测的精度，但神经网络算法需要大量的数据，也较容易陷入局部最优。文献[10～13]通过支持向量机算法对负荷进行预测，取得了一定的效果，但该方法对于多分类问题仍有局限性。

本文提出了一种改进粒子群优化的灰色傅里叶残差修正模型。首先对原始数据进行三点平滑法的预处理，减弱数据中异常值对预测的影响。灰色模型有效解决了原始数据不足的问题。然后通过改进粒子群算法对灰色模型中的参数适当优化提高预测精度。最后，通过傅里叶变换对残差的修正进一步提高了预测精度，并取得了理想的预测效果。

1 改进粒子群优化灰色-傅里叶残差修正模型

1.1 改进粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)是一种智能群体全局最优化的算法。PSO算法来源于鸟类群体捕食行为的研究，于1995年被首次提出。群体里的每个个体实时交流共享发现食物的位置，即为问题的最优解。其中任意一个个体就是问题的一个随机解，本文称其为一个“粒子”。不同问题具有不同的适应值函数(目标函数)，每个粒子都有其自身的适应值，且适应值的大小由问题的适应值函数决定。每一个粒子也都有其自身所在的位置和飞行速度以及飞行方向。每个粒子会按照一定的公式不断更新自身的位置和速度(矢量)，直至满足最终的终止条件。每次迭代过程中，每一个粒子都有一个其自身经过的最佳位置pbest和所有粒子经过的最佳位置gbest。最终经过比较找到位置最佳的那个粒子即为问题的全局最优解。具体建模过程如下文所述。

PSO优化算法中，首先初始化一群粒子的位置与速度。假设粒子群的初始群体大小为N，在S维空间中第i个粒子的速度和位置分别如式(1)和式(2)所示。

Di=[di1,di2,…,diS]

(1)

Vi=[vi1,vi2,…,viS]

(2)

通过粒子的适应值大小判断，来确定某一时刻每一个粒子所经过的最佳位置pbest和所有粒子经过的最佳位置gbest，分别表示为Oi(个体极值)和Og(全局极值)，如式(3)和式(4)所示。

Oi=[oi1,oi2,…,oiS]

(3)

Og=[og1,og2,…,ogS]

(4)

设目标函数为f(x)，故粒子i的最佳位置为

(5)

全部粒子所经过的全局最佳位置为

(6)

PSO算法每迭代一次，粒子的位置和速度都根据式(7)和式(8)更新一次，直到满足终止条件为止。

Vij(t+1)=ω(t)Vij(t)+c1rand(·)(Oij-Dij(t))+

c2rand(·)(Ogj-Dij(t))

(7)

Dij(t+1)=Dij(t)+Vij(t+1),

i=1,2,…,N;j=1,2,…,S

(8)

式(7)和式(8)中的w为惯性因子；rand()为(0,1)之间的随机数；c1、c2为取值(0,2)之间的学习因子；Dij(t)为第i粒子第t次迭代的位置。

PSO算法由于其具有概念简单、参数较少、易于实现的特点，在预测中被广泛应用。但PSO算法的收敛速度不佳且容易陷入局部最优。为了解决这个问题，本文提出了改进的PSO算法，即RWPSO。如式(9)和式(10)所示，改进的PSO算法将惯性因子在一定范围内随机取值，且去掉随机参数rand(·)。RWPSO算法降低了粒子的收敛速度，保持了粒子活性和算法的多样性。

Vij(t+1)=ω(t)Vij(t)+c1(Oij-Dij(t))+

c2(Ogj-Dij(t))

(9)

c1+c2>2(ω+1)

(10)

w(t)为惯性因子，是一定范围内的随机值，具体如式(9)所示。这样粒子速度既可以收敛又可以发散，保证了种群的多样性。

1.2 灰色模型

年度负荷原始数据具有一定的离散性，在原始数据进行灰色预测之前对数据进行一定的平滑处理可以有效降低噪声对原始数据的干扰，并增加原始数据的鲁棒性[14-18]。本文采用三点平滑法对数据进行预处理，其具体过程如下文所述。

设原始数据为X(0)=(x(0)(1),x(0)(2),…,

x(0)(n))，其中，x(0)(k)≥0，k=1,2,…,n。

(11)

其中，m=2,3,…,n-1。

两端数据单独处理为

(12)

(13)

原始数据经过三点平滑法的处理，降低了随机因素的影响。

灰色系统于1982年提出，该系统为部分信息已知、部分信息未知的系统。灰色系统通过已知信息建立微分方程模型，该微分模型统称为灰色模型，其建模过程如下文所述。

设原始数据为X(0)=(x(0)(1),x(0)(2),…,

x(0)(n))，其中x(0)(k)≥0，k=1,2,…,n；X(0)一次累加序列形成X(1)，X(1)=(x(1)(1),x(1)(2),… ,x(1)(n))，其中

(14)

其中，k=1,2,…,n。

对新序列X(1)建立微分方程

(15)

式中，a为发展系数，反映x(1)和x(0)的发展态势；u为内生控制灰数(亦称灰色作用量)。用最小二乘法确定参数a和u

[a,u]T=(BTB-1)BTY

(16)

其中，Y和B分别为

(17)

(18)

解微分方程得

(19)

其中，k=1,2,…,n。

对x^(0)(k+1)在经过累减运算，即

(20)

其中，k=1,2,…,n。

可得到原始负荷序列x(0)的预测值为

(21)

预测值与实际值的相对误差为式(22)。

(22)

1.3 改进粒子群优化灰色模型的建立

改进粒子群算法通过优化式(15)中发展系数a的最佳值来对灰色模型进行改进，以提高预测的精度。在该算法中，每个粒子代表了模型中的发展系数a的一个候选解an。粒子根据种群信息和个体信息在搜索空间中更新自身飞行速度和位置。在数次迭代后，最终找到一个发展系数a的最佳值，其流程如图1所示。

图1 改进粒子群优化的灰色模型流程图Figure 1.Flow chart of the grey model of RWPSO

具体步骤如下：

步骤1输入原始负荷序列到灰色模型中，为预测做准备；

步骤2初始化。随机产生N个粒子，对粒子的初始位置及初始速度进行设定；

Di=[ai,ui],i=1,2,…,N

(23)

Vi=[vi1,vi2],i=1,2,…,N

(24)

步骤3适应值计算。利用不同的a求出不同的预测值，代入目标函数式(25)中求出适应值；

(25)

步骤4根据位置计算式式(7)和速度计算式式(9)对粒子的位置和速度不断更新；

步骤5判断是否满足迭代的终止条件(是否大于最大迭代次数M)。若满足则输出最终的gbest和pbest，得到参数a的最佳值；否则返回步骤3；

步骤6将参数a的最佳值带入灰色模型求出预测值。

1.4 傅里叶残差修正

在电力系统中长期负荷预测的过程中，原始负荷数据往往有一定的离散性，这时用优化的灰色模型就会产生较大的误差。为了解决这个问题，本文提出了用傅里叶残差修正的方法对误差进行修正。

傅里叶残差修正是通过傅里叶变换对灰色模型预测数据的误差进行修正。傅里叶级数是一种有规律的周期性变化函数，具有消除随机噪声的作用。利用傅里叶变换对误差进行修正，可以有效削弱年度负荷原始数据中的噪声，进一步提高灰色模型在中长期负荷预测中的精度。具体修正过程如下：

(2)根据灰色模型的预测值和原始数据求出误差序列ε(k)=[ε(1),ε(2),…,ε(n)] ；

(3)将误差ε(k)用傅里叶变换表示为

(26)

(27)

(28)

k=2,3,…,n

(29)

式中，T=n-1；N=[(n-1)/2-1]；c0、cn、bn(n=1,2,…,N)为常数，又称其为傅里叶系数。将其整理为矩阵形式

E≈PC

(30)

其中

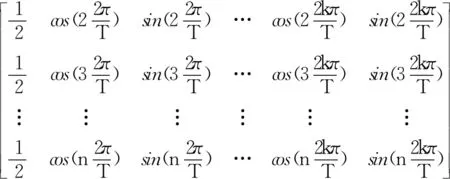
(31)

式中，E=[ε(1),ε(2),…,ε(n)]T为误差向量；C=[c0,c1,b1,…,cN,bN]T为傅里叶系数向量。由最小二乘法可得

C≅(PTP)-1PTE

(32)

(4)经过傅里叶修正的电力系统负荷预测为

(33)

2 组合模型

改进粒子群优化的灰色傅里叶残差修正电力负荷预测模型(FR-RWPSO-GM(1.1))的具体流程如图2所示。

图2 粒子群优化的灰色-傅里叶残差修正预测模型Figure 2.Gray-Fourier residual correction prediction model of PSO

该模型对中长期负荷预测的具体步骤如下：

步骤1初始化RWPSO算法中的参数(粒子数量、粒子的位置、速度和适应值)，并确定最大迭代次数；

步骤2用三点平滑法对原始数据进行预处理；

步骤3将预处理过后的数据输入GM(1.1)进行预测，并通过RWPSO算法求出最优的发展系数a；

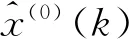
3 实例分析

以浙江省某地区2001～2018年的年度负荷为例，将2001～2012年这12年的实际年度负荷作为基础数据对2013～2018年的负荷数据进行预测。原始负荷数据如表2所示。

表1 浙江某地区2001～2018年原始负荷数据Table 1. 2001～2018 raw load data in a certain area of Zhejiang

图3 2001～2018年浙江某地区原始负荷Figure 3.The original load of a certain area in Zhejiang from 2001 to 2018

用三点平滑法对前12年原始负荷数据进行预处理，得到的数据如表2所示。

表2 预处理后的负荷数据Table 2. Load data after preprocessing

由图4可知，经过三点平滑法处理后的数据更加接近于线性关系。

图4 2001～2018年浙江某地区原始负荷及光滑处理后的数据Figure 4.The original load and smoothed data of a certain area in Zhejiang from 2001 to 2018

下面分别用灰色模型、数据平滑处理的灰色模型、数据平滑处理的粒子群优化的灰色模型、数据平滑处理傅里叶误差修正的粒子群优化的灰色模型对2013～2018年6年的年度负荷数据进行预测。在粒子群算法中取粒子数N=50，学习因子c1、c2取2，迭代次数M取200。预测结果如表3所示。

表3 2012～2018年浙江某地区年度负荷预测结果Table 3. Annual load forecast results of a certain area in Zhejiang from 2012 to 2018

图5 2012～2018年浙江某地区年度负荷预测结果Figure 5.Annual load forecast results of a certain area in Zhejiang from 2012 to 2018

由表3可知，粒子群优化的灰色傅里叶残差修正的中长期负荷预测模型的预测值，比灰色模型、数据平滑处理的灰色模型、数据平滑处理的粒子群优化的灰色模型更接近预测值，预测精度更高。

4 结束语

本文通过粒子群优化灰色傅里叶残差修正组合模型有效提高了中长期负荷预测的精度。原始数据经过三点平滑法的预处理，削弱了异常值对预测的影响。灰色模型通过粒子群算法进行参数优化，提高了灰色模型的预测精度，但预测精度仍不理想。采用傅里叶变换对误差进行修正，有效提高了预测精度。

该组合模型解决了文献[2～5]中时间序列分析法、灰色模型预测精度不足的问题，改善了文献[6]协方差稳健模糊线性回归分析法在处理纵向型数据时不够理想的问题。对比于文献[7～10]中的神经网络算法，粒子群优化灰色傅里叶残差修正组合模型不需要大量数据且不容易陷入局部最优。本文采用该模型对浙江省某地区的年度负荷进行预测，并与传统的灰色模型以及优化后的灰色模型进行比较。预测结果表明，该模型对中长期负荷预测效果较为理想，具有一定的有效性和可行性。