基于集合经验模态分解和ARIMA-GRNN的负荷预测方法
王洪亮,陈新源,赵雨梦
(昆明理工大学 电力工程学院,云南 昆明 650500)
智能电网作为研究热点受到越来越多的关注。用户是电网服务的对象,在智能电网中发挥着至关重要的作用。对用户侧数据进行采集、传输和存储,有利于管理电网发电需求。对用户负荷数据进行管理可以使电网更加安全可靠地运行[1]。电力负荷预测在保证电力系统安全及经济运行方面具有重要意义。进行负荷预测,需要建立与之对应的数学模型。随着负荷预测理论研究的不断深入,电力负荷预测的理论和方法也越来越多,例如神经网络、模糊理论、小波分析等[2]。但是这些方法仍具有局限性,例如神经网络算法要按照一定的准则进行学习,然后才能工作,而且容易出现陷入局部极小的现象。目前已有的负荷预测理论方法已无法满足预测速度和精度的要求,当计算数据非常庞大时,传统方法就显得力不从心,通常耗时几小时甚至几天。随着智能电网的发展,需要进行海量数据的收集、存储和处理,因此亟需一种新的大数据处理方法[3]。新型负荷的出现也对电网提出更高的要求,在大量数据基础上进行数据预测就显得十分重要[4]。在上述背景下,本文提出一种基于集合经验模态分解和ARIMA-GRNN的混合负荷预测模型,兼顾了电力负荷内在的线性特征与非线性特征,可以对电力系统负荷预测进行有效分析。仿真结果表明,该模型算法较之传统单一算法效果更加优越。
1 集合经验模态分解算法
经验模态分解(Empirical Mode Decomposition,EMD)法是一种新型自适应信号时频处理方法,适用于非线性非平稳信号的分析处理。EMD法依据数据自身的时间尺度特征来进行信号分解,无须预先设定基函数。集合经验模态分解方法(Ensemble Empirical Mode Decomposition,EEMD)是在EMD方法的基础上发展起来的[5]。该方法的本质是对时间序列数据进行局部平稳化处理,再进行希尔伯特变换获得时频谱图,从而得到有物理意义的频率[6]。EEMD的思想是信号极值点影响固有模态函数(Intrinsic Mode Function,IMF)分量,若分量分布不均匀则会出现模态混叠。将频谱均匀分布的白噪声引入要分析的信号中,可使信号自动分布到合适的参考尺度上。集成均值的计算结果与原始信号的差值随着集成平均次数的增加而减少[7]。由于零均值噪声的特性,噪声经过多次平均计算后会相互抵消,因此可将集成均值的计算结果视作最终结果。
EEMD算法步骤如下:
步骤1将正态分布的白噪声加到原始信号;
步骤2将加入白噪声的信号作为一个整体,然后进行EMD分解,得到各IMF分量;
步骤3重复步骤1和步骤2,每次加入新的正态分布白噪声序列;
步骤4将每次得到的IMF做集成平均处理后的结果作为最终结果。
由于受到天气变化、经济波动等多种外界因素的影响,负荷通常呈现非平稳序列的特征,所以必须对其采取平稳化处理。为了得到理想的预测结果,在数据进入模型的训练过程之前,需要对电力负荷的原始数据进行处理和分析。由于传统的信号分解方法对于分解非线性非平稳的负荷序列存在较大的局限性,故本文采用EEMD对原始负荷序列进行分解。
2 传统负荷预测方法
2.1 ARIMA时间序列模型
ARIMA为差分自回归滑动平均模型,又称为求自回归滑动平均模型,是时间序列预测分析方法之一。ARIMA时间序列法被广泛应用于电力系统负荷预测。该方法只需要通过前期的负荷数据便可以构建基于时间的数学模型,不仅计算速度快,计算过程简单,且只需少量数据就可以对平稳序列达到较高的预测精度。但是,如果负荷数据为非平稳序列,则需要在使用该方法前先实施平稳化处理[8]。
如图1所示,ARIMA模型是自回归模型AR模型和MA模型的整合模型,是一种常用的时间序列预测模型。其模型具体形式为

图1 ARIMA结构图Figure 1.ARIMA structure diagram
(1)
式中,t表示时间;yt为随时间t变化的原始负荷时间序列数据;Δdyt表示yt经d次差分后的平稳时间序列;εt表示随时间t变化的零均值的白噪声随机误差序列;Φi为AR模型第i阶的估计参数;p为AR模型的最佳阶数;θj为MA模型第j阶的估计参数;q为MA模型的最佳阶数。
基于ARIMA时间序列建模步骤如图2所示。如果负荷数据是一个非平稳的时间序列,则首先需要对时间序列做d阶差分,得到一个平稳的时间序列[9]。然后,对自回归阶数和滑动平均阶数尝试取值进行参数估计,利用AIC、BIC、HQC等信息准则挑选出最优的ARIMA预测模型。最后,利用挑选出来的最优ARIMA预测模型对负荷时间序列进行预测分析[10]。
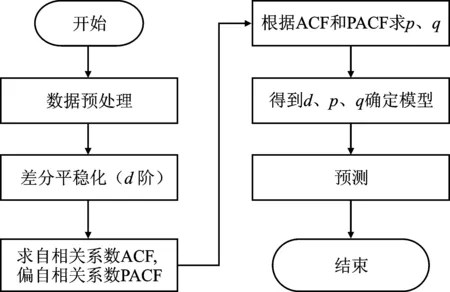
图2 ARIMA建模图Figure 2.ARIMA modeling diagram
2.2 GRNN神经网络负荷预测算法
广义回归神经网络(Generalized Regression Neural Network,GRNN)是一种径向基神经网络,具有很强的非线性映射能力和学习速度。GRNN最后收敛于样本量集聚较多的优化回归,当样本数据较少时,预测效果较好,还可以处理不稳定数据[11]。虽然GRNN没有径向基精准,但在实际分类和拟合方面,特别是在数据精准度比较差的时候,GRNN有着很大的优势[12]。
电力负荷预测是一个受诸多因素影响的具有随机性、非线性、动态不确定性的过程,对预测精度有一定的要求。针对天气、温度等随机因素对电力负荷的复杂影响,采用GRNN神经网络算法实现多种随机因素影响的短期电力负荷预测。由于GRNN神经网络具有较强的鲁棒性、非线性和自适应等特性,因此可以利用神经网络的学习能力来学习历史数据中包含的映射关系,再利用这种映射预测未来的电荷。
其中,X(x1,x2,…,xn)为输入;Y(y1,y2,…,yn)为输出。
如图3所示,GRNN神经网络结构包括输入层、模式层、求和层和输出层。输入层为向量,维度为m,样本个数为n,线性函数为传输函数。隐藏层与输入层全连接,层内无连接,隐藏层神经元个数与样本个数相等,也是n,传输函数为径向基函数。求和层中有两个节点:第一个节点为每个隐含层节点的输出和;第二个节点为预期的结果与每个隐含层节点的加权和。输出层的输出是第二个节点除以第一个节点的值[13]。

图3 GRNN结构图Figure 3.GRNN structure diagram
模式层函数为
(2)
式中,v为神经元;Pv为神经元v所在的模式层输出;X为网络输入变量;Xv为第v个神经元学习样本;σ为高斯函数的宽度系数,此处为光滑因子[14]。
求和层函数为
(3)
式中,n为神经元最大值;SD为求和层的输出。
对所有模式层神经元的输出进行算术求和,其模式层与各神经元的连接权值为1。
GRNN在逼近能力和学习速度上较其他神经网络算法有一定优势。GRNN最后收敛于样本量积聚较多的优化回归面,且在样本数据较少时具有较好的预测效果[15]。
3 基于EEMD和ARIMA-GRNN混合模型的负荷预测
电力系统负荷需求不仅包含时间序列变量,也受到温度、天气、经济等各种因素影响[16],进而产生非线性变量,如下式所示
Zt=Tt+Xt
(4)
式中,Zt为t时刻的观测值;Tt为t时刻的线性时间序列分量;Xt为t时刻的非线性预测分量预测值。
因此,无论是单一的时间序列算法还是非线性的神经网络算法,其对电力负荷预测都存在一定的局限性[17]。EEMD适用于非线性非平稳信号的分析处理[18-19]。本文提出了一种基于集合经验模态分解和ARIMA-GRNN混合模型的负荷预测方法,其具体建模过程如图4所示。

图4 EEMD-ARIMA-GRNN模型算法建模图Figure 4.EEMD-ARIMA-GRNN model algorithm modeling diagram
步骤1采用某地电网历史运行负荷数据作为样本原始数据,使用EEMD方法将样本原始数据分解出不存在模态混叠的IMF分量和余项;
步骤2ARIMA(p,d,q)模型分为AR、I、MA共3部分。使用ARIMA(p,d,q)模型对每一项IMF分量进行预测,首先需确定数据的差分阶数d。对样本数据进行一次差分就能得到一个平稳的负荷时间序列。负荷需求往往受到一些外界因素如天气或经济的影响,所以历史运行负荷数据一般表现为负荷数据时间非平稳时间序列;
步骤3对差分后平稳的IMF分量分别求得其自相关系数ACF和偏自相关系数PACF,通过对自相关图的分析,得到最佳阶层p。通过偏自相关图的分析,得到最佳阶数q。确定具体ARIMA(p,d,q)预测模型。利用选定的ARIMA预测模型对IMF分量进行预测分析得到预测数据。这些预测数据即为时间序列预测分量;
步骤4将通过步骤2得到的时间序列预测分量和样本原始数据相减得到非线性分量数据。取历史运行负荷每天的最高温度、最低温度、平均温度、平均相对湿度和降雨量特征作为GRNN神经网络算法的特征变量;非线性分量数据作为GRNN神经网络算法训练数据集和测试数据集。将训练数据集输入模块进行训练,反映这些特征变量对负荷的影响规律,得到训练模型。再利用训练模型对测试数据集进行测试,得到非线性预测分量预测值;
步骤5将所有时间序列预测分量和非线性预测分量两者相加,即可得到具有更高精度的电力负荷预测值。
为了更加直观地表明本文设计的复合模型的优越性,本文选取均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)和平均绝对百分误差(Mean Absolute Percentage Error,MAPE)3项数据来衡量预测模型的性能[16]。
RMSE是预测数据与实际数据差值平方和的算数平方根。均方根误差用来描述数据序列的变化趋势,其值越小,说明预测数值误差越小,计算式如下
(5)

平均绝对误差MAE和平均绝对百分误差MAP可用来衡量预测算法性能,其值越小说明算法越好。
(6)
(7)
4 算例分析
4.1 基于ARIMA时间序列的负荷预测
选取某地电网历史负荷数据,以2013年12月21日~2014年6月18日每天某个时刻共计180个数据作为样本数据。使用ARIMA(p,d,q)模型进行预测,通过对负荷数据进行一次差分得到一个平稳的负荷时间序列,即d为1。对差分后平稳的负荷时间序列分别求得其自相关系数ACF和偏自相关系数PACF,得到最佳阶层p为5,最佳阶数q为8。确定具体ARIMA(5,1,8),预测模型,进行预测分析得到预测数据,并与原始数据进行对比,得到原始数据与预测数据对比图和相对误差图,如图5和图6所示。

图5 ARIMA模型算法预测图Figure 5.ARIMA model algorithm prediction diagram

图6 ARIMA模型算法相对误差图Figure 6.Relative error diagram of ARIMA model algorithm
采用基于ARIMA时间序列的负荷预测,其预测趋势大致上与实际数据相同,但个别极值预测偏差过大,相对误差达到0.6,即在突发的外界因素条件影响下,采用单一的ARIMA时间序列的负荷预测方法不能满足预测精度要求。
4.2 基于GRNN神经网络算法的负荷预测
本文以2012年1月1日~2014年6月18日每天某个时刻共计900个数据作为样本数据,以2012年1月1日~2013年12月20日共计720个数据作为训练数据,以2013年12月21日~2014年6月18日每天某个时刻共计180个数据作为测试数据。取负荷数据每天的最高温度、最低温度、平均温度、平均相对湿度和降雨量特征作为GRNN神经网络算法的特征变量,将训练数据集输入模块进行训练,反映这些特征变量对负荷的影响规律,得到训练模型。然后,再利用训练模型对测试数据集进行测试,得到预测值,并与原始数据进行对比,得到原始数据与预测数据对比图和相对误差图,如图7和图8所示。

图7 GRNN模型算法预测图Figure 7.GRNN model algorithm prediction diagram

图8 GRNN模型算法相对误差图Figure 8.Relative error diagram of GRNN model algorithm
基于GRNN神经网络算法的负荷预测法的预测趋势与实际数据有较大差距,无法满足负荷随时间线性变化的特征,说明单一的神经网络算法同样无法满足负荷预测的精度要求。
4.3 基于ARIMA-GRNN混合模型的负荷预测
以2012年1月1日~2014年6月18日每天某个时刻共计900个数据作为负荷数据,先对其进行ARIMA模型预测,通过计算确定ARIMA(2,1,6)预测模型。然后,利用挑选出来的ARIMA预测模型对负荷数据进行预测分析得到线性预测数据,并与原始数据进行相减。将差值数据分为GRNN神经网络算法训练数据集和测试数据集,取负荷每天的最高温度、最低温度、平均温度、平均相对湿度和降雨量特征作为GRNN神经网络算法的特征变量。将训练数据集输入模块进行训练得到训练模型,再利用训练模型对测试数据集进行测试,得到非线性预测分量预测值。将非线性预测分量预测值和线性预测值相加得到最终预测值。原始数据与预测数据的对比图和相对误差图如图9和图10所示。

图9 ARIMA-GRNN模型算法预测图Figure 9.Algorithm prediction diagram of ARIMA-GRNN model
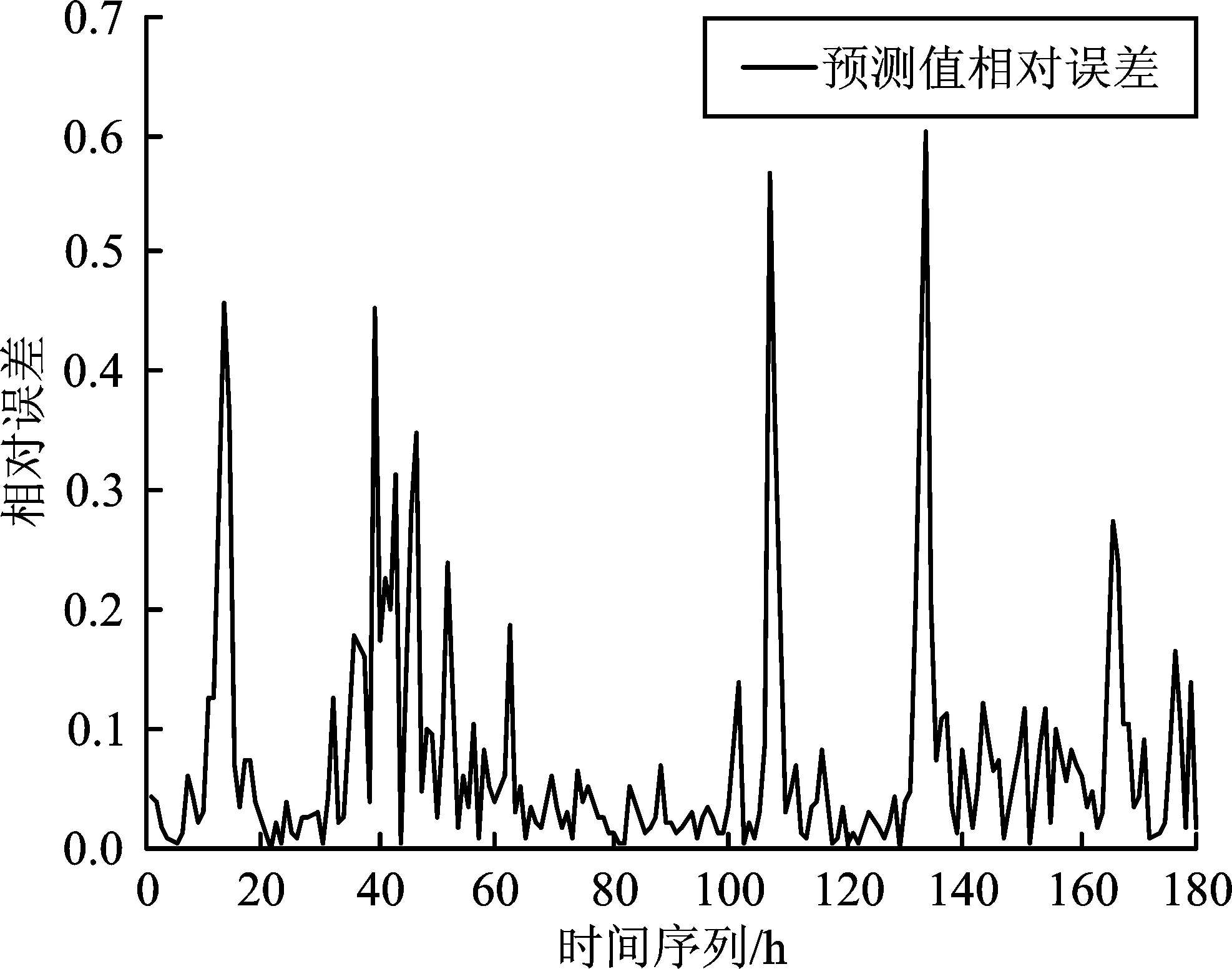
图10 ARIMA-GRNN模型算法相对误差图Figure 10.Relative error chart of ARIMA-GRNN model algorithm
采用基于ARIMA-GRNN混合模型算法进行负荷预测,其预测趋势大致与实际数据相同。相较于ARIMA方法,混合模型算法在负荷极点处的预测有了明显的改善,基本满足负荷预测的精度要求。
4.4 基于EEMD和ARIMA-GRNN混合模型的负荷预测
以2012年1月1日~2014年6月18日每天某个时刻共计900个数据作为样本数据,加入100组试验次数白噪音,白噪音标准偏差设置为0.2。通过EEMD将数据分解为IMF分量和余项,对每项IMF分量进行上述ARIMA-GRNN混合模型预测。将所有非线性分量与线性分量求和得到最终的预测值,如图11~图13所示。

图11 负荷数据EEMD分解图Figure 11.EEMD decomposition diagram of load data

图12 EEMD-ARIMA-GRNN模型预测图Figure 12.Algorithm prediction diagram of EEMD-ARIMA-GRNN model

图13 EEMD-ARIMA-GRNN模型算法相对误差图Figure 13.Relative error chart of EEMD-ARIMA-GRNN model algorithm
基于EEMD-ARIMA-GRNN混合模型算法的负荷预测的预测趋势与实际数据大致相同。在突发外界因素条件的影响下,极值处的预测值与实际数据相差较小,相对误差也控制在0.23以内,说明本文所设计的预测方法可同时兼顾电力负荷内在线性特征与非线性特征的特点,满足负荷预测的精度要求。
通过4次仿真实验得到4种预测算法的性能指标,如表1所示。

表1 性能指标表Table 1. Performance index
通过对表中数据进行分析,可知GRNN神经网络算法效果最差,传统ARIMA模型算法和ARIMA-GRNN算法的误差值次之。本文所提出的EEMD-ARIMA-GRNN混合模型算法性能最佳,3项数据均比传统ARIMA模型算法和GRNN模型算法更加优越。同时,对比4次仿真实验相对误差图,可以清晰地看出混合模型算法的相对误差在0.23之内,较大程度地提高了预测精度。综上所述可知,相较于传统单一算法,基于EEMD-ARIMA-GRNN混合模型的算法在电力负荷预测方面性能更优。
5 结束语
针对传统负荷预测方法难以兼顾电力负荷内在的线性特征量与非线性特征量的问题,本文提出了一种基于EEMD和ARIMA-GRNN的混合负荷预测模型方法。仿真实验证明,本文所提出的混合算法比传统的时间序列算法和单一的神经网络算法性能更加优越,能够满足短期负荷预测的要求。但是,本文所提方法并未考虑混合模型的计算开销及工程应用实际需求,下一步研究中将对上述问题进行探讨。

