引发某近坝库岸滑坡失稳临界蓄水位研究

余政兴，孙 宁

(中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014)

自1963年意大利瓦依昂滑坡发生后，库岸滑坡，尤其是近坝库岸滑坡一直是国内外学者研究的重点[1]。水库蓄水后，近坝库区水位变化幅度最大，滑坡体前缘被水淹没后稳定性降低，若发生失稳，对水库大坝的安全运行和下游城镇均会造成巨大威胁。

长期以来，大量学者在库岸滑坡的形成条件和预测评价等方面进行了大量研究。Zou Zongxing等[2]基于对三峡库区滑坡监测数据分析，提出了水库滑坡变形机制的解释模型；李卓等[3]对近坝库岸滑坡进行了模型试验研究，揭示了水库运营情况下滑坡土压力、孔隙水压力、基质吸力等变化，对此类滑坡破坏特点进行了总结；张永刚[4]基于流固耦合的三维数值模拟方法，对三峡库区不同降水速率滑坡破坏过程进行了研究；吴泉澳[5]、王灏[6]等基于FLAC3D的强度折减法，对不同降雨量、不同蓄水位下滑坡的稳定性进行了研究。

以上研究均建立在水库建设期或运营期的库水位调度对滑坡影响的基础上，而在蓄水位尚未确定的规划阶段，针对不同设计蓄水位对库岸滑坡的影响少有研究。若在水库或流域梯级规划阶段就考虑对近坝库岸不良地质体问题，则可通过调整设计方案等方式提前预防，能极大减轻后期治理工程的工作量。本文在前人研究的基础上，基于某水电站近坝库岸大型滑坡，在假定蓄水位尚未确定的情况下，对引发滑坡失稳的临界蓄水位进行研究，以期为水库规划及后期防治工作提供参考。

1 研究区概况

1.1 工程概况

某水电站地处藏区，为I等大(1)型工程，正开展前期勘察工作。该工程在流域规划阶段曾采用310m的高坝方案，蓄水位2605.00m，但考虑到高坝建设难度大等原因，目前设计采用低坝方案，正常蓄水位2535.00m，死水位2530.00m。由于区域内工程地质条件复杂，河谷狭窄，岸坡陡峻，在近坝库岸形成了多处不良地质体。其中Z1滑坡体位于拟选坝址上游左岸，距离坝址约1.7Km，为坝址区内规模最大、危害性最大的滑坡体。

1.2 基本地质条件

1.3 气象水文

研究区地处高山峡谷区，为干热河谷气候，气温高，降雨少，由于河谷内发育局部小气候，与附近气象站差异较大，故对区内气象进行实测。2014—2020年实测多年平均气温16.0℃，最高气温36.7℃，多年平均降水338.3mm，最大日降雨量33.5mm。研究区内地下水主要为基岩裂隙水，钻孔揭露地下水位较低，基本与河水位平齐(河面常水位2367m)，监测显示，暴雨期间地下水位上升幅度最大可达15m，但仍位于滑坡体以下。

1.4 滑坡体发育特征

Z1滑坡体前沿高程2500m，后缘最高约3110m，最大高差达610m，平面分布面积约35.6万m2，滑体一般厚度28m左右，总方量约996.8万m3，为大—巨型滑坡。滑坡中后部滑体较厚，揭露最大厚度可达57m，为中—深层推移式滑坡。滑面地形整齐、坡度35°左右，以中间冲沟为界将滑坡体分为Ⅰ、Ⅱ两区，其中Ⅱ区后缘见少量裂缝。滑体、滑带组成物质以碎石土为主，滑床为坚硬的花岗岩，滑坡体边界清晰，自然条件下基本稳定。

1.5 成因机制分析

滑坡体目前处于蠕滑变形阶段，后缘见少量拉裂缝，其产生变形的原因主要为滑体规模较大，结构松散，在重力作用下，滑体与基岩面产生相对位移。除此之外，滑坡的形成条件还包括了地形地貌、地质构造、岩土性质、水文地质等内在因素，以及地震、降雨、地下水位变化、河水位变化、人类活动等外在诱因。

针对Z1滑坡，在天然条件下，自重应力对滑坡体的形成起主导作用；而降雨、地震、库水位作用等是促使滑坡体失稳的诱发因素。由于库区降雨稀少，附近不具备发育6级以上地震条件，周围亦多见有垂直自稳高度超10m的堆积体，故地震与降雨对滑坡体影响有限，仅在极端情况下考虑。水电站运营蓄水后，库水位变化与滑坡体稳定性关系最密切，其主要体现在：库水位的上升使坡体岩土体浸水软化，物理力学强度降低；库水位上升对坡体产生浮托力；同时库水位变化使坡体内地下水位发生改变，进而使得坡体内产生渗流作用，影响库岸滑坡的稳定性。

故本文主要从库水位变化对库岸滑坡形成的影响角度出发进行研究。

2 不同蓄水位条件下滑坡体稳定性评价

2.1 渗流求解

渗流求解的主要目的是确定某一时刻的浸润线，浸润线确定后可以通过水头求解坡体内孔隙水压力的变化，为坡体后期的强度、变形及稳定性分析奠定基础。浸润线的求解方法主要有Boussinesq方程法[7]、Forchheimer方程法[8]、实际监测法、以及基于SEEP/W模块的渗流—应力非完全耦合法[9- 10]。其中Boussinesq方程法、Forchheimer方程法求解较为困难，故本文首先基于监测数据推测稳定蓄水后的坡体的浸润线，再通过Geostudio的SEEP/W模块，对库水位变化后的渗流过程进行二维数值计算，进而得到库水位变化后的浸润线。

由于地区降雨量稀少，实测发现地下水位基本与河水位平齐，故假设正常蓄水稳定后坡体地下水位仍与库水位平齐，而在水库运营时地下水随库水位的变化而改变。据统计，约60%的滑坡发生在库水位骤降时期，其余40%发生在水位上升或稳定蓄水时期[11]，通常又以水位骤降时滑坡稳定系数最低[12]，故本文仅对不同设计蓄水位下水位骤降时滑坡的稳定性进行对比。由于该水电站是以发电为主的日调节水库，可调节水位5m左右，故对稳定蓄水后水位骤降5m(骤降速率为5m/d)的浸润线进行求解，考虑到滑坡Ⅰ区位置相对较低，更易受到库水位影响，故取A—A＇剖面作为计算剖面，蓄水位取2535m时初始孔隙水压力分布如图1所示。

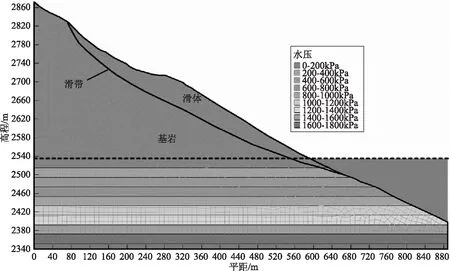
图1 初始孔隙水压力分布

进行瞬态分析前需要定义土水特征曲线，即水力传导率函数曲线和体积含水量函数曲线，其中土体参数设置如图2所示。根据渗透室内试验和压水试验结果设置渗透系数，土体饱和渗透系数Ks=4.8m/d，基岩Ks=0.01m/d。

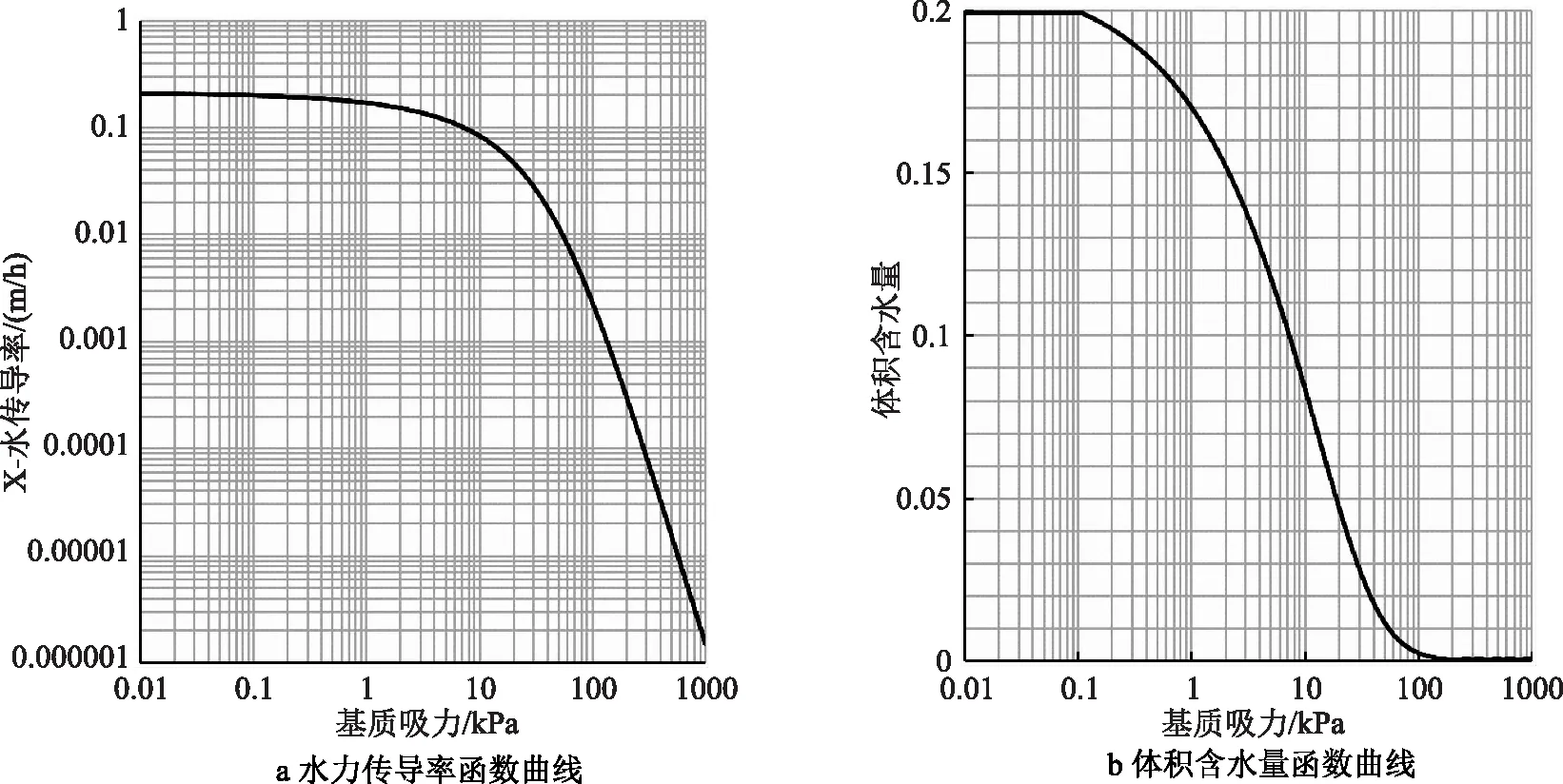
图2 土体渗流参数设置

定义临水坡面为水头边界，底部为不透水边界，左右垂直端为零流量边界，对模型进行瞬态渗流求解(降水5m，速率为5m/d，时间24h)，渗流进行24h后浸润线变化情况如图3所示。可见坡体内部水位有所降低，而基岩、滑带处水位降低不明显。

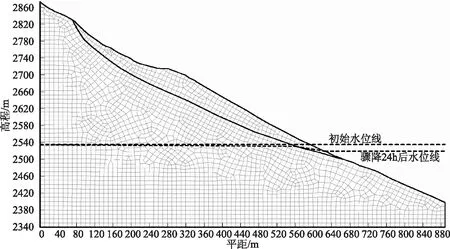
图3 降水24h浸润线

2.2 稳定系数计算

在渗流计算完成的基础上，采用传递系数法对滑坡整体的稳定性进行计算，基于室内试验、参数反演、经验等取值，计算参数见表1，其中浸润线以上取天然参数，以下取饱和参数。由于该水电站曾分别考虑过高坝方案(蓄水位2605m)和低坝方案(蓄水位2535m)，现以10m梯度分别求解蓄水位2535～2605m之间库水位骤降5m时滑坡整体的稳定性。

表1 滑坡稳定性计算参数

计算结果如图4所示，在蓄水位为2535～2605m时，滑坡稳定系数随水库蓄水位的增高而降低，平均蓄水位每升高10m，滑坡稳定系数降低约0.017。在目前采用的低坝方案(蓄水位2535m)中，水库蓄水后滑坡稳定系数为1.071，处于基本稳定状态；而若采用高坝方案(蓄水位2605m)，蓄水后滑坡稳定系数仅为0.948，极可能发生失稳。故仅从对近坝库岸稳定性影响考虑，采取低坝方案更有利。当蓄水位位于2465～2575m时，滑坡稳定系数在0.997～1.012之间，处于临界稳定状态，内插可得滑坡失稳的临界蓄水位约2571m。

图4 不同蓄水位稳定性计算结果

3 基于FLAC3D的滑坡三维数值模拟

由于滑坡规模较大，实际地形地貌与地质条件较复杂，滑坡变形破坏模式还不明确，而二维计算仅能代表滑坡剖面附近的稳定性情况，有较大的的局限性，故需采用三维数值模拟软件对二维计算结果进行验证和推广。本文采用FLAC3D有限差分数值软件，对不同蓄水条件下滑坡稳定性进行评价，并对滑坡破坏过程、破坏模式等进行演化。

3.1 模型建立

采用外接软件建模后导入FLAC3D进行计算，模型如图5所示，分为滑体、滑床、基岩3个部分，划分网格数554244个，对滑带、滑体内的网格进行了加密处理。

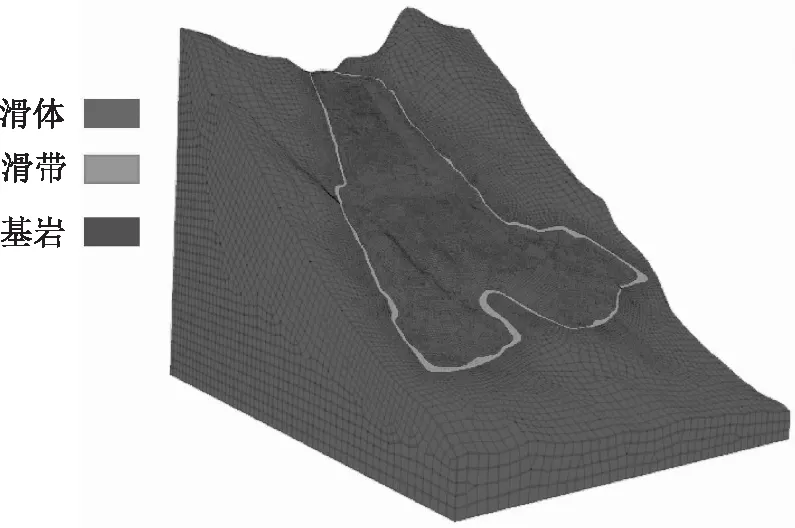
图5 三维计算模型

滑坡的荷载组合从两个方面考虑，即自重力和水作用力，其中水作用力考虑水库水位变化对滑体稳定性产生的影响，浸润线参照2.1节设置，滑坡迎水面施加等效于库水压力的应力。分别对未蓄水及蓄水位2535、2571、2605m四种情况下水位骤降5m工况进行计算，除表1所给的岩土参数外，其余计算参数见表2。

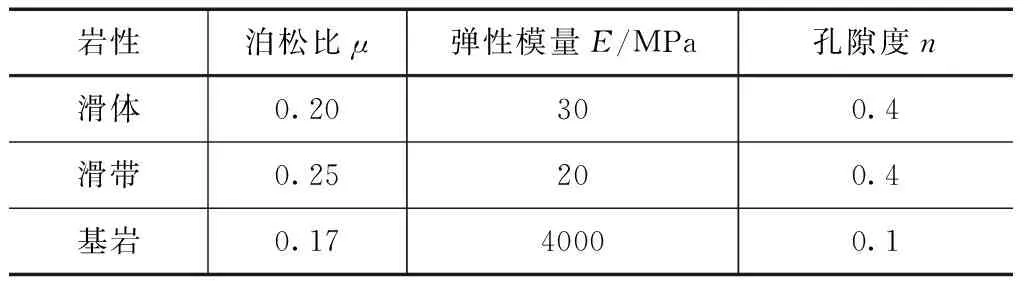
表2 数值模拟计算参数

本次计算模型选用莫尔-库仑模型，计算满足莫尔—库仑破坏准则。

3.2 计算结果分析

FLAC3D计算完成的标志是最大不平衡力趋于0，如图6所示，当最大不平衡力减小至1x10-6Pa以下，说明在天然重力场条件下，模型通过自身的调整可以达到自平衡，天然应力场形成。

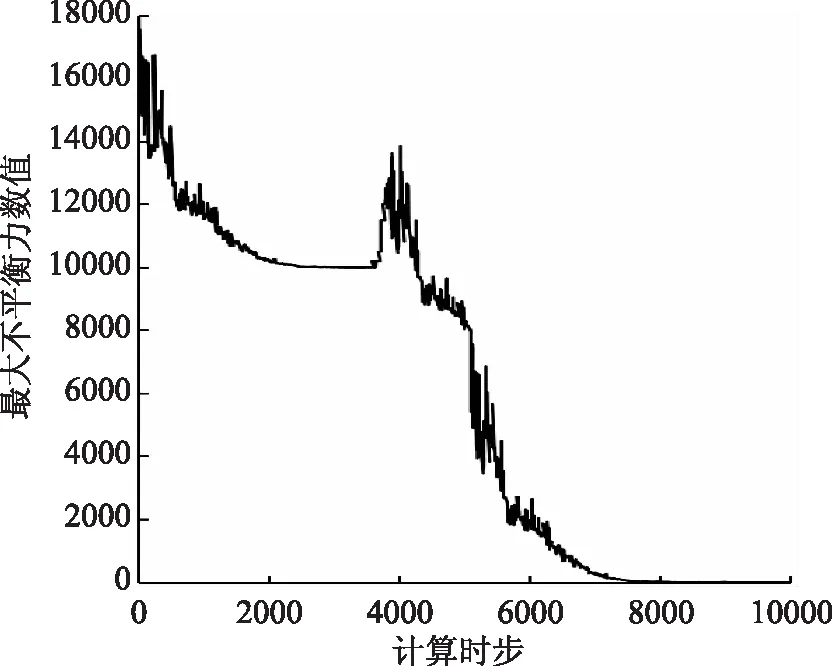
图6 最大不平衡力曲线

首先对蓄水前滑坡应力、应变场情况进行分析。未蓄水时滑坡的应变云图如图7所示，可见当前滑坡变形主要集中在坡体中后部，前缘为阻滑段，与推移式滑坡的特点相吻合。中部变形最大为0.2m，考虑到中部土体较厚，主要为土体沉降产生的垂直位移，而沿滑动方向变形较小，说明此时滑坡尚处于蠕滑阶段。对B—B′位置进行切片后，调出最大剪应力云图，如图8所示，可见滑体、滑带内最大剪应力基本小于50kPa，尚未达到坡体的抗剪强度，故滑坡目前基本稳定。

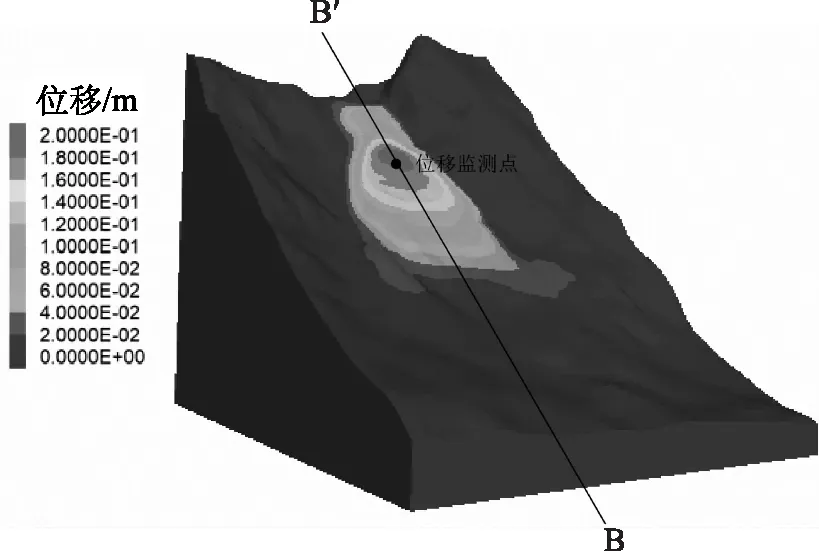
图7 蓄水前滑坡位移云图

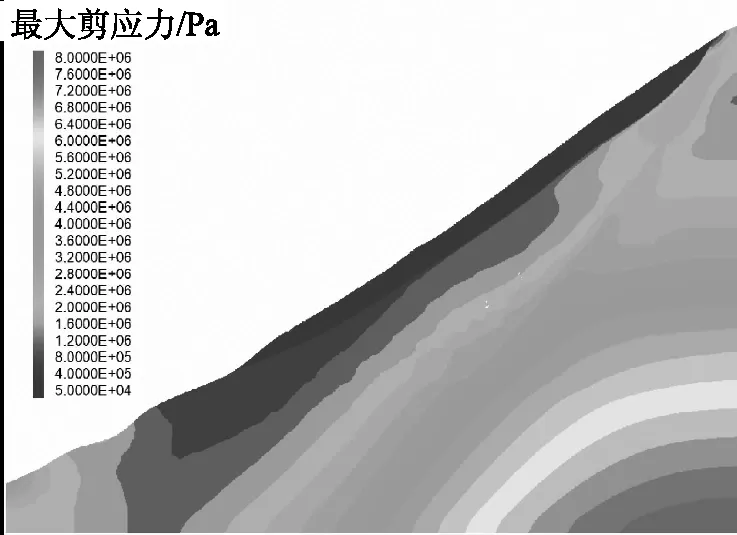
图8 最大剪应力分布云图

FLAC3D中通常以塑性区的贯通性作为滑坡是否失稳判据。各工况滑坡体的塑性区分布如图9所示，由图9可知，未蓄水时，滑坡仅Ⅱ区中后部侧边界有少量塑性变形，变形体长度约40m，宽度约2m，与实际中滑坡出现裂缝位置基本对应，此时滑坡基本稳定；蓄水位为2535m时，Ⅱ区侧边界塑性区范围扩大，有逐渐连通趋势，Ⅰ区边界开始出现少量塑性变形；蓄水位为2571m时，滑坡后缘塑性区基本连通，I区坡脚等位置出现少量塑性变形，实际Ⅰ区内已经出现连通的塑性变形面，此时滑坡处于欠稳定—临界稳定状态；蓄水位为2605m时，滑坡边界位置塑性区完全贯通，滑带内出现剪应力塑性变形。此时对B—B′剖面位置进行切片处理，滑坡体内最大剪应变增量分布如图10所示，可见滑坡剪应变增量主要集中在滑带位置，前、后缘已完全贯通，滑坡沿滑带整体剪切破坏，坡体已发生失稳。对蓄水前后坡体中部的位移进行监测，如图11所示，蓄水至2605m时坡体最大位移已增加至12m，说明滑动后部分坡体已产生堆积。

图9 塑性区分布云图

表3 稳定系数计算结果

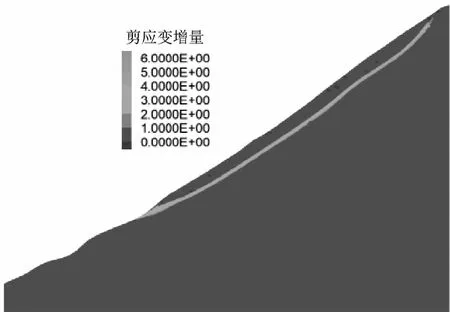
图10 最大剪应变增量云图

图11 坡体中部位移监测曲线

不同蓄水位下滑坡的破坏状态也反应了滑坡失稳的演化过程，具体为：滑体前缘为阻滑段，下滑力主要来自于滑坡中后部土体，随着库水位升高，前缘被水淹没，地下水渗透入滑带中，前缘滑带力学性质降低，使阻滑作用降低。此时在后缘坡体巨大推力作用下，前缘逐渐被推动导致坡体整体破坏。其破坏过程可总结为：蠕滑、拉裂、剪切、滑动4个阶段。

Flac3D内置了稳定系数计算方法，即强度折减法，计算中通过不断降低抗剪强度折减系数Fs，将折减后的力学参数重新带入模型计算，直到模型发生破坏，此时的抗剪强度折减系数Fs就是滑坡的安全系数F。该功能可通过调用FOS命令进行计算，计算结果见表3。与基于传递系数法的二维计算结果相比，三维数值模拟结果偏大。除了与内置算法不同外，这主要由于二维计算仅考虑了单条剖面位置的局部失稳，而三维计算更注重滑坡的整体性稳定性，故三维计算的结果与实际情况更相符合。

4 结论

(1)该近坝库岸滑坡为重力主导型滑坡，水库蓄水是其失稳主要诱发条件。在设计蓄水位为2535(低坝方案)～2605m(高坝方案)时，蓄水位高度与滑坡稳定性呈负相关，具体为：在未蓄水时，天然条件下滑坡处于基本稳定；在蓄水位为2535m时，滑坡稳定系数有所降低，但仍处于基本稳定；当蓄水位达到2571m时，滑坡处于临界稳定；蓄水位达到高坝方案设计蓄水位2605m时，滑坡发生失稳破坏。

(2)三维数值模拟结果证明了该滑坡为上部土体挤压下部产生变形的推移式滑坡，滑动发育过程主要包括了蠕滑、拉裂、剪切、滑动4个阶段，蓄水后加快了滑坡变形发育的速度。

(3)三维计算滑坡稳定系数稍高于二维计算结果，这是由于三维数值模拟相比于二维计算更着重于滑坡的整体稳定性，其结果与实际情况也更相符。结合两种分析方法，可对滑坡的成因模式和发育趋势进行相对准确的预测。

(4)仅从对近坝库岸的稳定性方面考虑，该工程目前所采用的低坝方案(蓄水位2535m)更有利，但蓄水后滑坡稳定性仍有降低，需做好长期监测工作。本文使用的分析方法也可推广到类似工程中，可为水库、流域梯级等规划及后期防治工作提供参考。