蓄水位差对沭新北船闸工程沉降影响及预测分析
唐子明,徐 瑞,王 淼,董鸿伟
(江苏省淮沭新河管理处,江苏 淮安 223001)
0 引 言
我国现今中大型水闸约5 000座[1], 在灌溉、环保、防洪、水力发电、航运等方面发挥着至关重要的的作用。然而,中大型水闸在运行过程中,安全会受到多种因素的影响,其中水闸地基不均匀沉降便是其中之一[2]。这是由于一些水电站闸址区常修建于黏土地基之上,而在水电站蓄水之后,水闸前后存在水位差,导致地基产生过大或不均匀沉降,使水闸与底板之间产生拉应力,严重威胁水闸的安全运行[2]。因此,分析蓄水水位差对船闸工程沉降的影响,是水闸安全运行的关键问题之一[3]。
目前,国内外通常采用数值模拟的方法来分析地基沉降或者与建筑结构之间的相互作用,常用的数值理论包括有限元法[4]、有限差分法[5]、离散元法[6]等。王泽志[7]利用流体力学软件,以海河闸为例, 建立海河防潮闸三维数学模型,研究地面沉降因素对防潮闸水力特性的影响规律,获得了在不同沉降量时的防潮闸闸下流态、流速及流量变化规律。王涛等[8]以某进水闸为例, 通过ABAQUS软件对加固前后的地基沉降进行了数值模拟分析,得到加固前后粉砂地基的沉降规律。李路华[9]利用ABAQUS有限元软件,结合具体的工程实例进行三维建模计算,模拟分析了某护镜门型式水闸底板采用闸墩分缝和底板分缝时, 对于不同的荷载工况,其相应的受力及变形情况,为工程提供设计依据。缪圆冰等[10]针对苏州河河口水闸闸底板差异沉降小于1.5 cm的设计要求, 建立水闸整体三维有限元模型,并进行多方案数值模拟,给出了控制差异沉降的有效方法。丁立魁[11]利用ABAQUS有限元软件对吹填区内一水闸工程进行了基于共同作用理论的上部水闸结构-基础-软基的整体数值分析。
本文以沭新北船闸工程为例,采用ABAQUS建立三维船闸与地基模型,先将不同蓄水水位下,船闸底板的实测沉降与数值模型中的沉降进行对比分析,验证模型的可靠性;再通过模型预测分析多种蓄水水位条件下,船闸工程各监测点沉降规律,其研究结果可为相关工程分析提供参考。
1 工程位置
沭新北船闸位于宿迁市沭阳县桑墟镇青伊村境内,上游为沭新河,下游为黄泥蔷薇河,是分淮入沂综合利用沭新河工程之一,与沭新南船闸一起沟通淮沭新河与连云港市航运,尚可承担沭新河向黄泥蔷薇河补水的任务。沭新北船闸隶属于江苏省淮沭新河管理处,由蔷薇河地涵管理所管理。工程位置见图1,图2为沭新河流域水系图。
图1 沭新北船闸工程位置图

图2 沭新河流域水系图
2 模型建立与计算参数
沭新北船闸上闸首尺寸为 22.0 m×25.0 m(长×宽),闸首顶高程为▽8.50 m(20 年一遇洪水位+风浪高), 闸门顶高程▽8.10 m,底板底高程▽-3.50 m,底板厚为2.50 m。输水廊道尺寸为2.50 m×2.0 m,廊道底高程为▽-1.0 m。下闸首尺寸为 22.0 m×25.0 m(长×宽),闸首顶高程为▽8.50,闸门顶高程▽8.10 m,闸墩控制楼段顶高程为 8.50 m,两侧闸顶高程为7.5 m,底板底高程▽-3.50 m,其余尺寸与上闸首保持一致。
经现场初勘查明,钻探深度范围内的土层可分为6 个工程地质层:①填土层:上部成分较复杂,以壤土、 粉质壤土为主,中下部以黏土、粉质黏土为主(可塑或可塑~硬塑状),层厚 0.6~9.0 m, 层底高程-1.24~4.83 m;②粉质黏土层:灰褐色,软塑~可塑状,层厚0.2~0.6 m,层底高程3.51~3.77 m;③粉质黏土层:灰褐色、灰黄色,可塑状,层厚 0.5~1.7 m,层底高程 2.41~3.27 m;④粉质黏土层:灰黄色、黄色,以硬塑状为主,局部可~硬 塑状,夹礓结石(较富集),层厚 3.0~9.0 m,层底高程-5.87~-3.28 m;⑤轻砂壤土层:灰黄色,稍湿~湿,中密状,夹礓结石局部夹粉质黏土,层厚1.3~3.1 m,层底高程-7.15~-4.78 m;⑥黏土层:黄色、暗黄色,硬塑状,无摇震反应,有光泽,干强度及 韧性高,含氧化铁粉末,夹礓结石(较富集),勘察深度范围内未揭穿该层。图3为本次概化模型,表1为本次计算力学参数。

图3 船闸概化三维模型
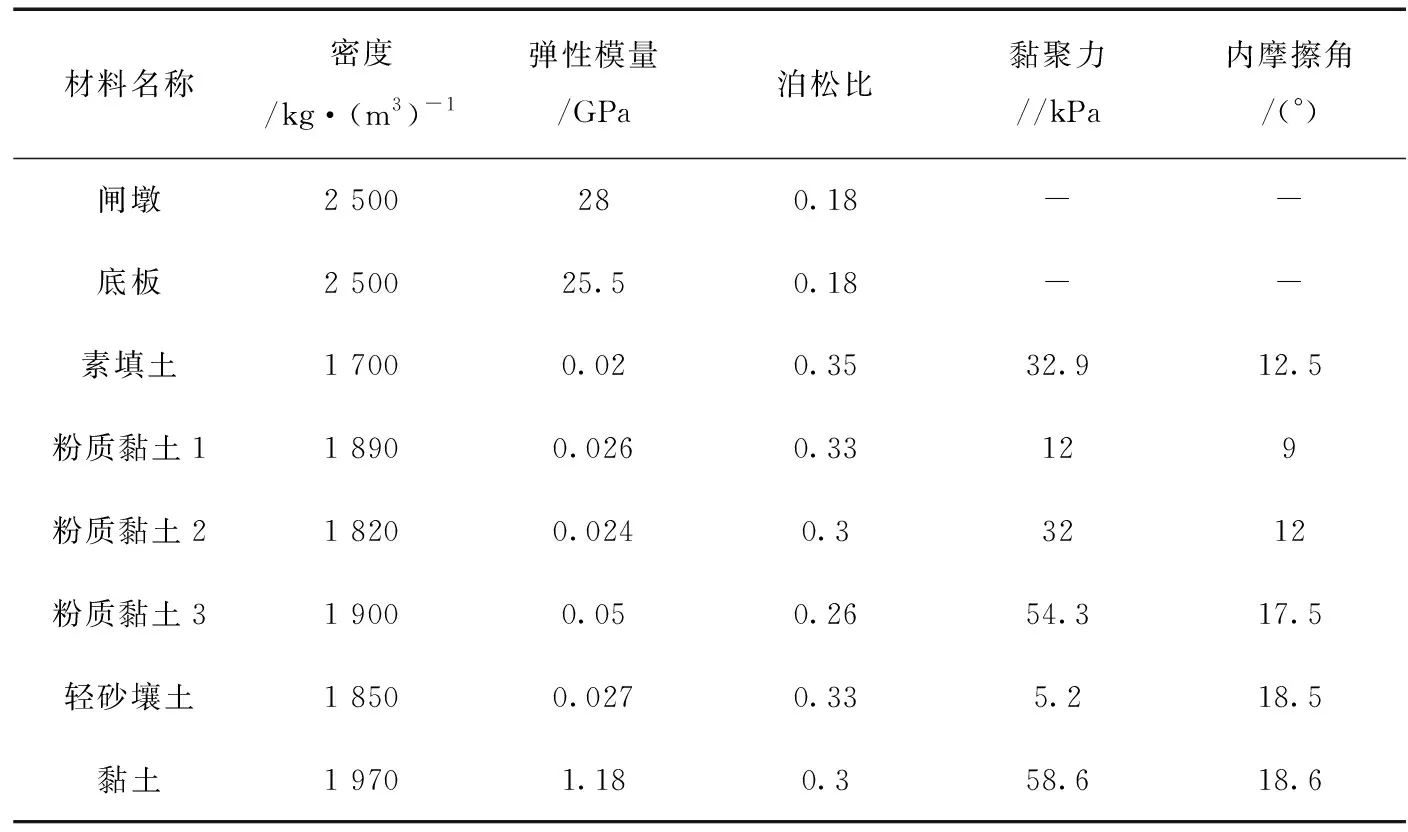
表1 模型计算力学参数
3 数值分析结果与实测沉降对比
沭新北船闸引河断面观测每年汛前一次。水下部分采用过河索法,断面距采用100 m标准测绳观测,水深采用测深锤观测,断面河宽直接从测绳读取。本工程共设56个垂直位移观测标点,3个工作基点,垂直位移观测采用DNA03型电子水准仪,观测等级三级,观测精度符合要求。
本文以2021年的6次蓄水位差的观测结果为基准来验证数值模型的可靠性,实测结果见图4。图5为本次不同蓄水位差下数值结果误差。由图5可知,当蓄水位差为4.13 m时,上闸首与底板2的实测沉降与数值结果相差最大,约为16.8%;当蓄水位差为3.86 m时,上左翼的误差最大,为15.1%;当蓄水位差为3.57 m时,下闸首、底板1、下左翼的沉降误差最大,分别为10.3%、11.3%和16.6%。监测点的实测沉降与对应的数值模型中的沉降最大误差为16.8%,最小误差为1.5%,总体上小于20%。因此,本次建立的数值模型可以用于预测不同水位差下的整个船闸工程不同部位的沉降。

图4 不同蓄水位差下的实测沉降
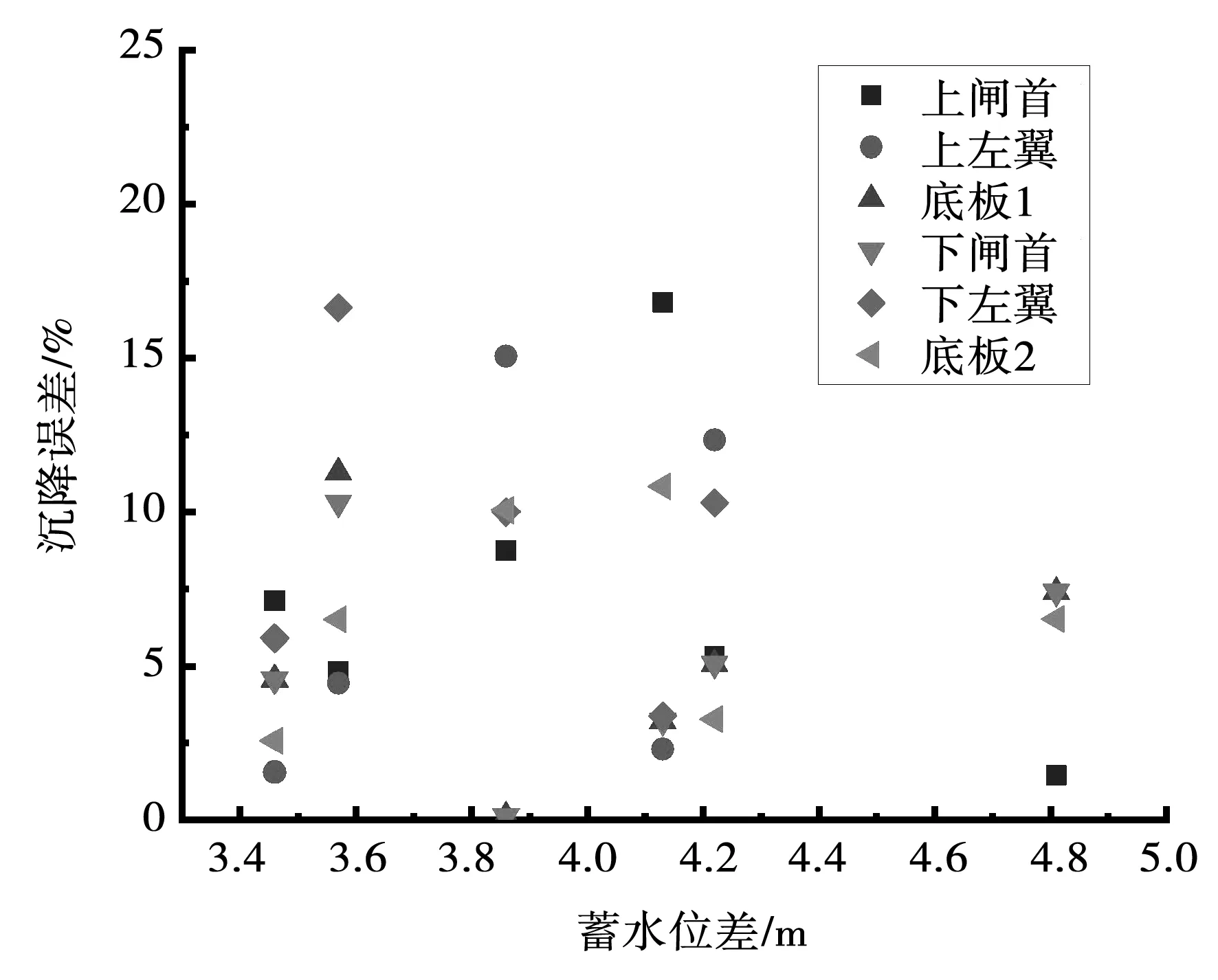
图5 不同蓄水位差下的数值结果误差
4 不同蓄水位差下各监测点沉降预测
本文根据多年的监测数据,一共设计15种蓄水位差来分析整个船闸工程的沉降,见图6。图6中最大蓄水位差5.9 m,最小蓄水位差2.25 m。

图6 15种不同蓄水位差
图7为不同蓄水位差下的上闸首预测沉降。由图7可知,当蓄水位差为5.9 m时,上闸首的沉降最大,为3.8 mm;而当蓄水位差为2.3 m时,沉降最小,为0.08 mm。此外从图7中还可看到,不同蓄水位差下的上闸首沉降变化趋势并不相同,当蓄水位差在[2.66, 2.74]、[3.49, 3.83]、[5.26, 5.61]这3个区间时,上闸首的沉降变化趋势最陡,沉降增长最快。

图7 不同蓄水位差下的上闸首预测沉降
图8为不同蓄水位差下的上左翼预测沉降。由图8可知,当蓄水位差为5.9 m时,上左翼的沉降最大,为2.2 mm;而当蓄水位差为2.3 m时,沉降最小,为0.1 mm。此外,当区间蓄水位区间在[3.23, 3.49]时沉降增长最快。从图8中的数据还可得出,同一蓄水位差下,上闸首与上左翼的沉降并不一致。说明不同蓄水位差下,地基产生了明显的差异沉降,容易造成底板底部产生拉应力,导致翼墙开裂。

图8 不同蓄水位差下的上左翼预测沉降
图9为不同蓄水位差下的底板1与底板2预测沉降。由图9可知,底板1与底板2的最大沉降存在一定差值,其中在蓄水位差为,5.9 m时,底板1的最大沉降为1.99 mm,而底板2的最大沉降为1.87 mm。蓄水位差在区间[3.43,5.42]时,两者的沉降差和增长趋势几乎保持一致;但当蓄水位差小于3.42 m时,底板1与底板2的沉降对水压力的响应并不相同,两者沉降差较大。

图9 不同蓄水位差下的底板1与底板2预测沉降
图10为不同蓄水位差下的下闸首预测沉降。在图10中,当蓄水位差达到最大时,下闸首的最大沉降为3.95 mm;当蓄水位差为2.25时候,沉降仅为0.03 mm。其中,当蓄水位差在区间[3.23,5.26]时,下闸首的沉降增长较为缓慢,几乎保持不变;而当蓄水位差大于5.26 m时,下闸首的沉降增长趋势最快。

图10 不同蓄水位差下的下闸首预测沉降
图11为不同蓄水位差下的下左翼预测沉降。由图11可知,下左翼的总体沉降趋势与下闸首相似,存在沉降缓冲区和沉降加速增长区。其中,当蓄水位差在区间[3.8,5.61]时,沉降增长速度明显较缓;而当蓄水位差大于5.61 m,增长速度较快。本案例中,当蓄水位差为5.9 m时,下左翼沉降最大,为2.63 mm。

图11 不同蓄水位差下的下左翼预测沉降
5 结 论
本文以沭新北船闸工程为例,采用ABAQUS建立了三维船闸与地基模型,先将不同蓄水水位下,船闸底板的实测沉降与数值模型中的沉降进行对比分析,验证模型的可靠性;再通过模型预测分析了多种蓄水水位条件下,船闸工程各监测点沉降规律。结论如下:
1) 当蓄水位差为5.9 m时,各监测点的沉降最大,分别为上闸首3.8 mm,上左翼2.2 mm,底板1为1.99 mm,底板2为1.87 mm;而下闸首与下左翼分别为3.95 mm和2.63 mm。
2) 同一蓄水位差下,各监测点的沉降并不一致。说明不同蓄水位差下,地基产生了明显的差异沉降,容易造成底板底部产生拉应力,导致翼墙开裂和闸首变形。

