基于ANSYS仿真计算的渡槽结构静动力特征分析研究

李 密，吕 锋，曾祥磊，田均兵

(贵州省水利水电勘测设计研究院有限公司，贵阳 550002)

1 概 述

水工建筑安全稳定性不仅与静力荷载有关[1]，同样地震动力工况下结构应力、位移响应值亦较为关键[2]，因而系统性探讨水工结构静动力特征对提高水工设计水平具有重要价值。李宁霄[3]、孙洪亮等[4]利用水工结构原型复制，在室内完成水工模型搭建，设立相应的水工荷载，安装相关渗流、应力与位移监测传感器，分析水工结构在运营过程中静力场与渗流场变化特征；而针对动力工况，主要采用振动台试验仪器，完成水利结构振动台试验[5]，以模拟地震下结构监测数据，分析水工设计参数优化问题。物理模型试验需要成本且周期较长，无法较高效获得结构不同设计方案下的静动力特征。因而，一些学者利用ANSYS[6]、ABAQUS[7]以及COMSOL[8]等有限元软件建立计算模型，模拟计算不同设计方案、不同工况下结构渗流场以及静动力下响应特征；而流固耦合工况下，亦可采用有限元仿真手段完成计算模型的多物理场叠加[9]，分析模型应力、位移等变化特征。本文根据黔西拟建水工渡槽结构静动力响应特征问题，利用ANSYS完成结构静力荷载下位移、应力分析，获得地震荷载下模态特征与应力响应特征，为工程安全设计提供重要依据。

2 工程概况

为提升地区水利安全性，黔西地区拟建一水工渡槽，承担地区水资源调度、通航等作用。黔西水工渡槽设计最大流量为80 m3/s，采用拱式截面，净高为14.5 m，设计拱顶轴线延伸系数为1.3，截面曲率为3×10-4。该弯拱在主槽结构设置有4孔预制箱涵，单孔宽度为6 m，高度2.5 m，顶、底板厚度分别为0.6、0.4 m，腹板厚度以及缝宽均根据设计方案优化后确定为0.3、0.35 m，该渡槽中部剖面图见图1。为确保渡槽运营后长期稳定性，工程设计部门拟对该结构开展运营期流固耦合状态下静动力特征开展分析，以确保渡槽设施满足工程运营安全要求。

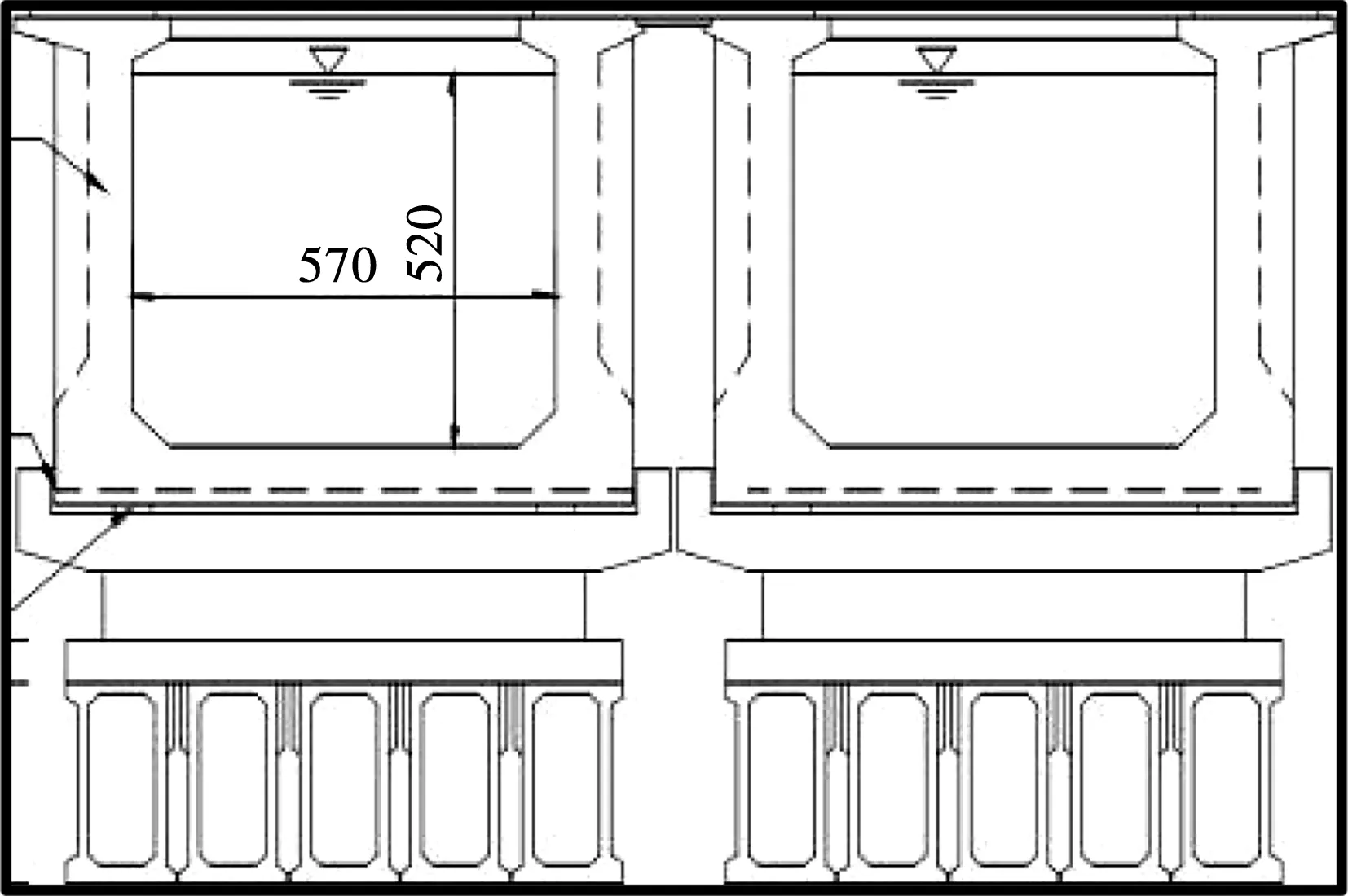
图1 渡槽中部剖面图

3 渡槽结构流固耦合下静力特征

3.1 工程建模

利用ANSYS仿真计算平台按照水工渡槽设计方案建立几何模型[10]，见图2。该模型包括主槽、弯拱、支撑柱以及连系梁等结构，其中拱脚与立柱部分为固结连接，槽身与支撑系统间布设弹性支座。采用六面体微单元作为网格基础单元体，利用ANSYS划分几何模型后，获得渡槽有限元模型，见图3，共获得微单元42 628个，节点数36 828个。为分析方便，本文计算模型中X、Y、Z正向分别为主槽水流向、主槽横轴右岸向以及渡槽垂直向上。设定模型中水槽流速为2.5 m/s，计算渡槽无水工况(1#工况)、半水位工况(水位2.8 m、2#工况)以及设计水位工况(水位5 m、3#工况)下主槽静力场特征。

图2 渡槽几何模型

图3 渡槽有限元模型

3.2 位移特征

根据对3种不同工况下渡槽主槽位移计算，获得渡槽各截面上位移变化特征，见图4。

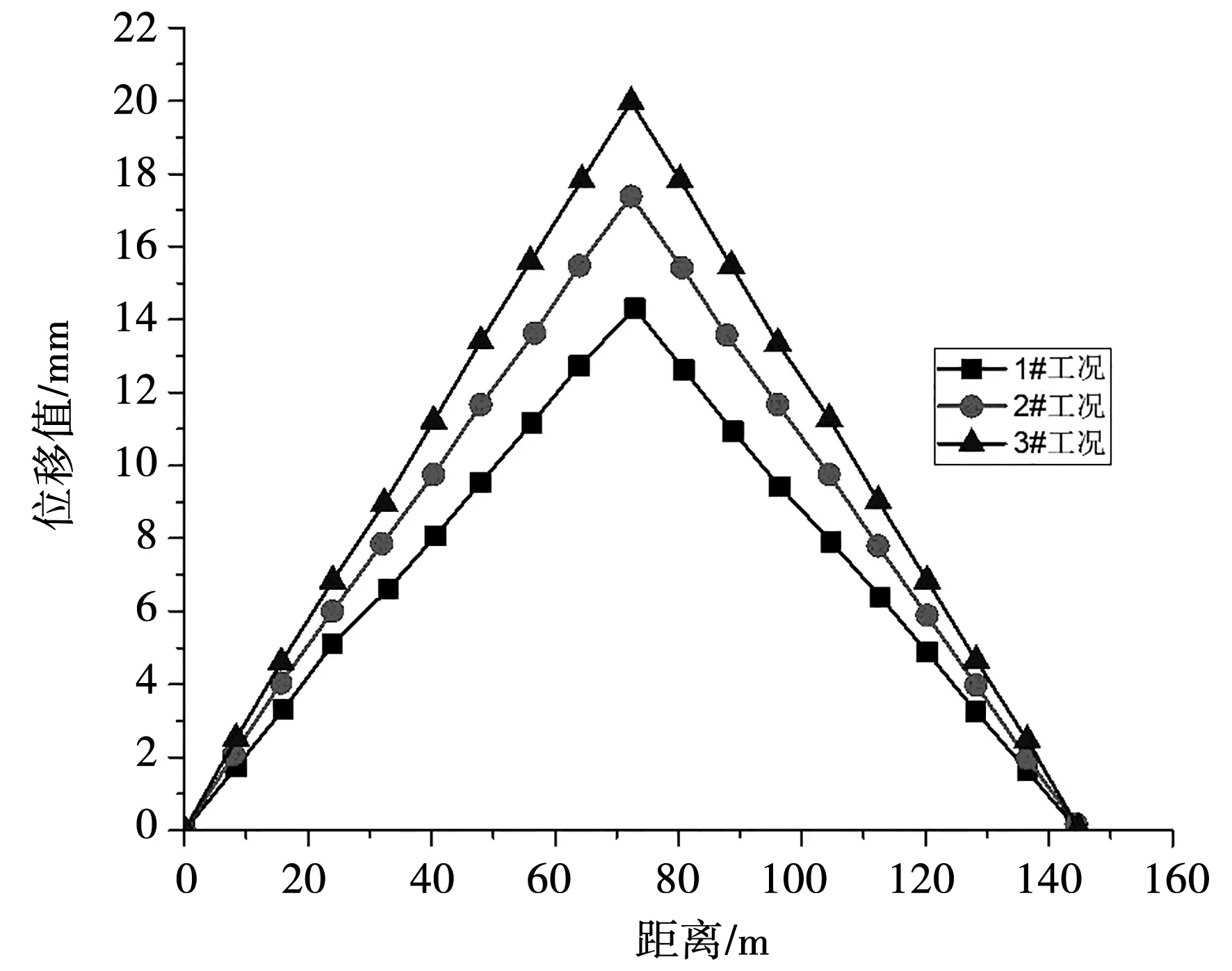
图4 渡槽各截面上位移变化特征

从图4中可知，3种工况下主槽各截面上Z向位移曲线均为倒V形，以水槽中部80 m处位移最大，1#-3#工况下中部最大位移分别为14.3、17.4和20 mm；当水槽截面距离在左岸至中部区间内时，各工况下Z向位移均为递增态势，3个工况下位移平均增幅分别为32.2%、32.5%和32.4%，而在主槽中部至右岸方向，位移递减至0，即Z向位移在渡槽两岸均为0。对比不同工况下位移特征可知，以3#工况下位移值最大，其在主槽各截面上位移值相比1#、2#工况下增幅分别达34.1%～51.7%、14.4%～25.7%。分析认为此与渡槽内水体自重有关，在静力荷载下，当槽内自重愈大，则在弯拱中部造成的挠度愈大，而本文中3#工况水位最大，在不考虑流速影响下，3#工况结构承受荷载最高，因而其造成的主槽位移值亦愈大。从3个工况下位移差幅可知，最大差幅出现在主槽跨中，而在主槽两岸截面上工况间位移差幅较小，随靠近主槽跨中，各工况间位移差幅愈大；在截面40 m时3#工况上位移值为11.2 mm，相比1#、2#工况下位移增幅分别为38.9%、14.9%，而在截面70 m处3#工况与1#、2#工况间位移增幅达41.3%、18.5%。该模型中采用的弯拱渡槽，从结构力学角度考虑，弯拱是承受荷载主要结构，因而其最大挠度出现在弯拱结构处，而愈靠近两岸承载较低，位移差异性亦较小。从结构安全性角度考虑，因重点对弯拱结构的底板、腹板等主要承载部位进行加固处理，在主槽中部增设预应力型钢结构，提升中部承受荷载变形的刚度。

3.3 应力特征

为分析渡槽结构静力工况下应力特征，计算获得3个工况下主槽截面上拉应力分布，见图5。从图5中可看出，3#工况上拉应力最大，达4.655 MPa，位于腹板处，而1#、2#工况下最大拉应力相比前者分别减少28.8%、13.1%，表明3#工况中受水体自重影响，具有较大弯矩，因而在主槽底板结构处产生较大拉应力集中。各工况下拉应力分布基本接近，主槽腹板结构部位处拉应力也存在较大，1#工况中腹板部位拉应力以0.313～1.438 MPa为主，而在2#工况中腹板部位的拉应力增长27.8%～4.6倍，而3#工况中相比该部位拉应力增长至0.472～2.041 MPa。在腹板与底板接触区域，各工况下均存在有较大拉应力，2#工况中该区域拉应力分布为2.224～2.679 MPa，此与渡槽结构腹板部位存在有支撑拉杆效应，造成该部位截面上存在“下拉上压”的应力分布效应，因而结构设计时该部位应重点加密布设钢筋。在渡槽中部拉应力集中在底板，而往渡槽两岸方向，拉应力分布逐渐蔓延至腹板部位，且拉应力分布有近对称分布形态，而水位愈高，则渡槽结构体系中产生的拉应力威胁面愈大，表明不可忽视水体自重在渡槽运营期间产生的拉应力效应。从应力安全性考虑，2#、3#水位工况下最大拉应力均超过4 MPa，已达到结构安全允许临界值，主槽结构产生张拉裂缝趋势较大，因控制主槽腹板与底板接触区域，再次印证应加大结构刚度，确保水槽运营安全性。

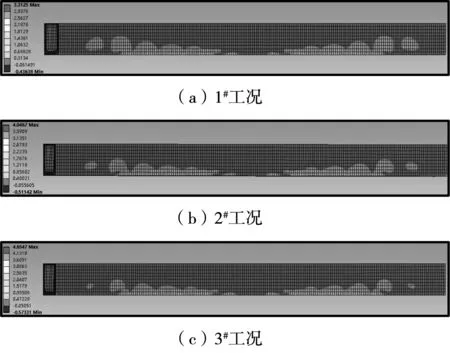
图5 主槽截面上拉应力分布

4 渡槽结构流固耦合下动力响应特征

4.1 地震荷载模型

利用ANSYS完成渡槽结构地震动力荷载下建模，见图6，以附加质量模型作为建模基础，水体自重叠加处理，完成流固耦合下渡槽地震荷载模型建立。本文动力响应工况中，以1#无水工况、3#设计水位工况开展对比分析。

图6 地震荷载渡槽模型

4.2 自振特性分析

根据对有、无水工况下渡槽结构自振特性分析，获得主槽自振频率特征，见图7。从图7中可知，两工况下自振频率变化趋势基本一致，均呈先慢后快增幅态势，在计算第1-第5阶次区间内，平均增幅为25.8%，而在计算阶次超过5后，平均增幅为36.6%，表明结构自振频率在荷载后期更为显著。当处于3#有水工况下，计算阶次在第1-第5与第5-第10区间内，各阶次下自振频率平均增幅分别为30.3%、35.3%。对比两工况下自振频率可知，1#无水工况自振频率高于3#有水工况，此与水体自重有关，当主槽内水位愈高，受水体自重影响，其频率降低[11]。

图7 主槽自振频率变化特征

4.3 动力响应特征

针对渡槽结构动力响应特征，设计以弯拱结构作为重点分析对象，探讨该结构地震荷载下应力响应特征，并以弯拱上拱脚、1/2处、拱顶作为特征部位开展分析，所引入的地震荷载反应谱曲线见图8。

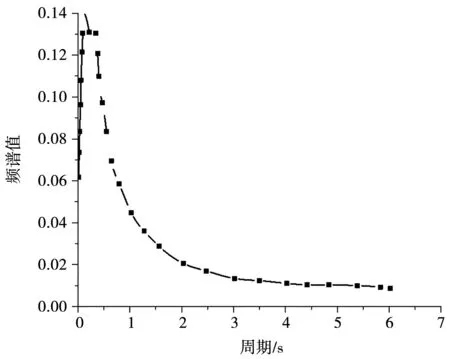
图8 地震荷载反应谱曲线

本文根据地震荷载反应谱曲线分别设定不同方向荷载，引入主槽水流向、横向、竖向3个不同输入方向的地震荷载计算模型，分别得到特征部位应力响应值，见图9。从图9中可看出，在无水工况中拱脚处应力响应值最大，属竖向输入模型，达6.3 MPa，而水流向与横向方向上相同部位处应力值相比前者分别减少44.4%、76.2%。而在弯拱1/2处部位最大应力为4.7 MPa，仍属竖向输入荷载模型，而水流向、横向该部位最大应力仅为前者的68%、22%。有水工况下3个特征部位应力响应值均有提高，在横向输入荷载模型中，3#工况拱脚处应力响应值相比1#无水工况下增长4%，而在横向输入荷载模型中，特征部位间应力差幅为4%～25.7%；顺水流向与竖向荷载模型中特征部位应力差幅分别为8.3%～70%、23.8%～46.8%，由此可见竖向输入荷载模型中有、无水体差异性最显著，此与流固耦合下竖向荷载与水体自重方向相一致，耦合作用下结构应力响应值显著增大。

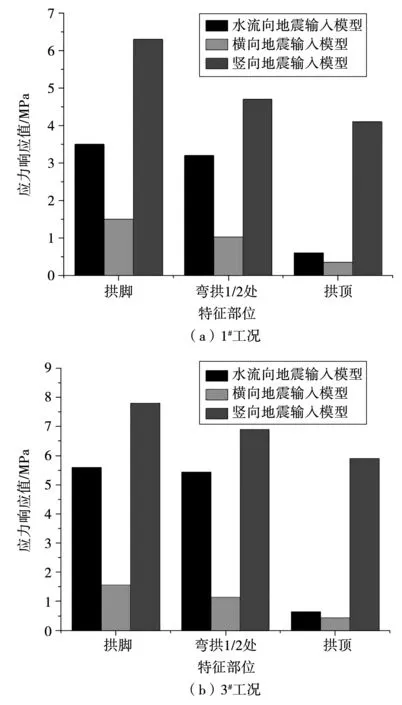
图9 主拱应力响应值

拱顶处最大应力亦为竖向输入荷载模型，达4.1 MPa，水流向、横向与其差幅为5.8倍、10.7倍；分析表明竖向输入地震荷载下弯拱结构应力响应最显著，受张拉破坏威胁最大。

5 结 论

1) 主拱中部80 m处位移最大，而两岸侧位移均为0，1#-3#工况下最大位移分别为14.3、17.4和20 mm；受水体自重影响，3#工况下位移值最高；愈靠近主槽跨中，各工况间位移差幅愈大，主槽截面40 m处3#工况与1#、2#工况位移差幅分别为38.9%、14.9%，而在跨中截面位移差幅增大至41.3%、18.5%。

2) 静力荷载下3#工况拉应力最大，达4.655 MPa，位于腹板处；渡槽中部拉应力位于底板，两岸侧拉应力分布至腹板部位。

3) 动力荷载下有、无水工况自振频率的变化特征一致，呈先慢后快增幅，且无水工况下自振频率高于有水工况。

4) 3种不同输入方向地震荷载下，竖向输入

模型应力响应值最大，无水工况下拱顶处水流向、横向与其差幅为5.8倍、10.7倍；且该荷载输入模型中有、无水工况下差异性最显著，特征部位上应力差幅达23.8%～46.8%。