基于ANSYS Workbench的弧形闸门流固耦合数值分析
李炳阳,杨旭亮
(1. 中国电建集团北京勘测设计研究院有限公司,北京 100024;2. 青海民族大学 土木与交通工程学院,青海 西宁 810007)
弧形闸门作为水利工程中重要的泄流控制结构,其在水下的动力特性及泄流过程中的结构响应对评判闸门结构的安全性与设计合理性至关重要,目前对此问题的分析手段主要有原型观测、模型试验与数值模拟。原型观测可直接在结构上进行试验和响应采集,其结果最为直接、真实,但需要闸门建成后方可进行;模型试验(全水弹性)可全面模拟水动力特性、闸门结构体系动力特性及水流-结构耦合动力效应,但水弹性材料的阻尼比与泊松比难以满足相似准则要求而需进行反馈修正[1],且建模和试验的周期一般也较长;伴随计算机及计算方法的发展,数值模拟研究进展较为迅速,既可分析闸门结构流固耦合自振特性,也可进行多种复杂物理条件下的流场模拟,进一步实现流固耦合响应分析。
在流固耦合数值分析方面,国内外许多学者进行了大量的研究工作。古华等[2]利用声学流体单元模拟门前水体,取得了流体对平板闸门结构自振特性的影响规律,探讨了流固耦合液相长度的取值范围;B Hübner等[3]研究认为对于水下结构由于附加质量效应产生的频率降幅的确定,忽略水体流动而以声学流体模型分析是足够的;袁宝珺[4]通过建立三维有限元数值模型,对平面钢闸门的干、湿模态进行了计算分析;董爱玲[5]利用ANSYS有限元分析软件建立了闸门-流体耦合模型,开展了平面钢闸门流固耦合作用下自振特性分析;盛旭军等[6]利用ANSYS软件建立了弧形闸门有限元模型,并对闸门整体模态进行了计算分析;王学亮等[7]利用ANSYS Workbench进行弧形钢闸门三维有限元分析,得到两种工况下闸门主要构件应力和位移分布;刘竹丽等[8]以ANSYS-Workbench软件采用双向流固耦合方法对平面钢闸门流激振动特性进行了模拟,得到了闸门不同开度下的位移、应力情况;王磊等[9]采用ANSYS-CFX软件对流场中的拦挡坝结构进行单向流固耦合数值分析,得到流速、压力等流场数据和坝体应力、位移等结构响应;张凡等[10]以泄洪冲沙弧形闸门为例,利用ABAQUS软件并基于耦合欧拉-拉格朗日理论(CEL)建立了水体-弧形闸门流固耦合模型,获得了闸门位移、应力和接触力等的变化分布规律。
本文基于通用有限元ANSYS Workbench平台,以声学流体模型直接耦合法和单向耦合法分别对某工程放空底孔弧形闸门在水下的动力特性及泄流条件下流体结构响应进行数值分析,对比模型试验测得的水力荷载,验证泄流工况下单向流固耦合数值模拟的可行性,并在此基础上进行了泄流激励下的结构响应分析。
1 流固耦合控制方程
目前,解决流固耦合问题所采用的方法主要有直接耦合法和顺序耦合法。前者通过把流固控制方程耦合到同一方程矩阵中求解,需要利用包含所有必须自由度的耦合单元类型;后者将流体域和结构域的控制方程在时空上交替迭代,耦合作用不同步,通过流固交界面实现流体域和结构域计算结果的交换传递。流固耦合分析所采用的基本控制方程如下。
(1)流体控制方程
流体流动遵循基本的物理守恒定律,主要包括质量守恒、动量守恒和能量守恒定律。描述一般可压缩牛顿流体的质量与动量守恒定律控制方程如下。
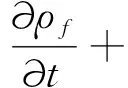
(1)
式中,ff—体积力矢量;ρf—流体密度;v—流体速度矢量;τf—剪切力张量。
(2)结构控制方程
结构部分的守恒方程由牛顿第二定律导出。
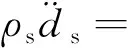
(2)
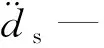
(3)流固交界面方程
(3)
2 直接耦合自振特性分析
2.1 水体-闸门相互作用的耦合方程
利用声学流体单元直接耦合法计算自振特性时,需考虑流体N-S方程及连续性方程,以ANSYS欧拉法中的位移-压力格式,对水体作如下假定:①流体是无旋、无黏的且无热交换;②流体是均质的、可压缩;③小变形,流速远小于流体中的声速,如此得到以压力p为目标函数的波动方程。
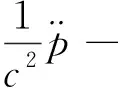
(4)
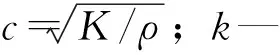
引入相应的边界条件,采用Galerkin法离散上述方程,可得水体的动力平衡方程[7]。
(5)
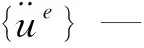
将交界面压力荷载向量代入结构动力平衡方程。
(6)
从控制方程(5)—(6)可以认为,流体与结构在界面处的相互作用引起声压施加给结构一个强迫力,而结构运动将产生一个有效的“流体荷载”,将动力平衡方程合在一起写成分块矩阵形式,即可得闸门-库水相互作用的流固耦合方程。
2.2 计算模型与边界条件
某工程放空底孔出口顶部按1∶4的坡度收缩,出口尺寸3.2m×5.5m,底槛高程为110.0m,工作闸门门型为潜孔式弧形闸门,门叶结构为主纵梁式,材料Q345钢,支承为直支臂圆柱铰支铰;闸门需动水启闭,启闭设备采用QHSY型液压启闭机,启门力为1000kN,闭门力为300kN,扬程为7.5m,采用镀陶瓷活塞杆液压缸。对止水结构和材料模型进行简化,侧止水与顶止水与面板按绑定处理;闸门采用三维实体单元Solid185模拟,弹性模量200GPa,密度为7850kg/m3,泊松比0.3;水体采用三维流体声单元Fluid30模拟,水体密度为1000kg/m3,水中声速1430m/s,水体长度20m。放空底孔弧形闸门-水体耦合整体有限元模型如图1所示。

图1 闸门-水体模态耦合模型
在交界面上设置流固耦合面,通过单元关键项设定Absent与Present控制水体自由度,即交界面上水体单元的节点有压力自由度和3个位移自由度,远离交界面的水体单元只具有压力自由度;放空底孔位于水下而无自由液面,而选取的计算水体为有限长度,所以将远场水体设置为无限边界。
2.3 结果分析
选取开度e=0.2、1.0、2.0、3.0、4.5m五种计算工况,分别计算弧形闸门在无水和有水情况下不同开启程度时的自振特性,各开度下启闭杆第一阶和闸门结构前三阶频率见表1。各阶振型描述如下:第1阶为启闭杆XY面一阶弯曲振动;第2阶为启闭杆轴向拉伸及侧向弯振,闸门整体绕支铰XY平面内振动;第3阶为左右支臂YZ平面内弯振;第4阶为启闭杆、闸门整体连同左右支臂XY平面内弯振。其中XY面为水流向平面,YZ面为垂直水流向平面,闸门1阶和4阶湿模态振型如图2所示。
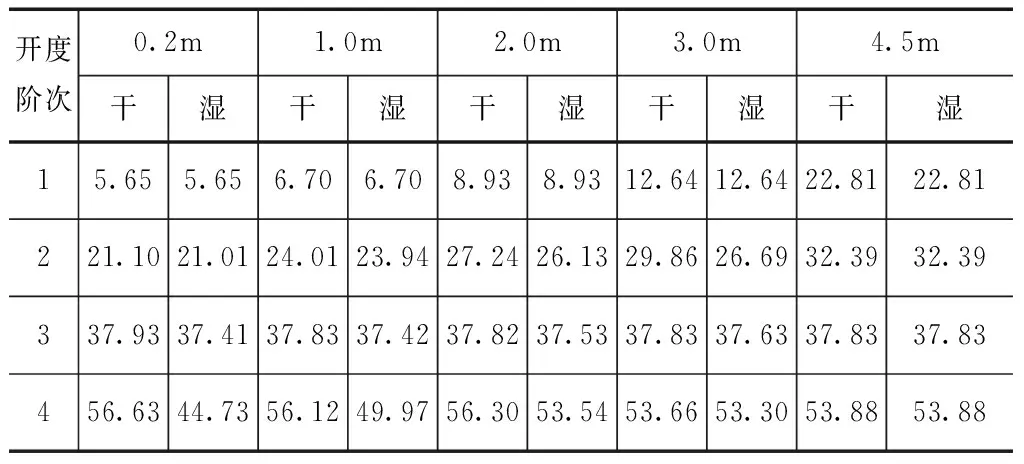
表1 不同开度下弧门干、湿模态前4阶频率 单位:Hz
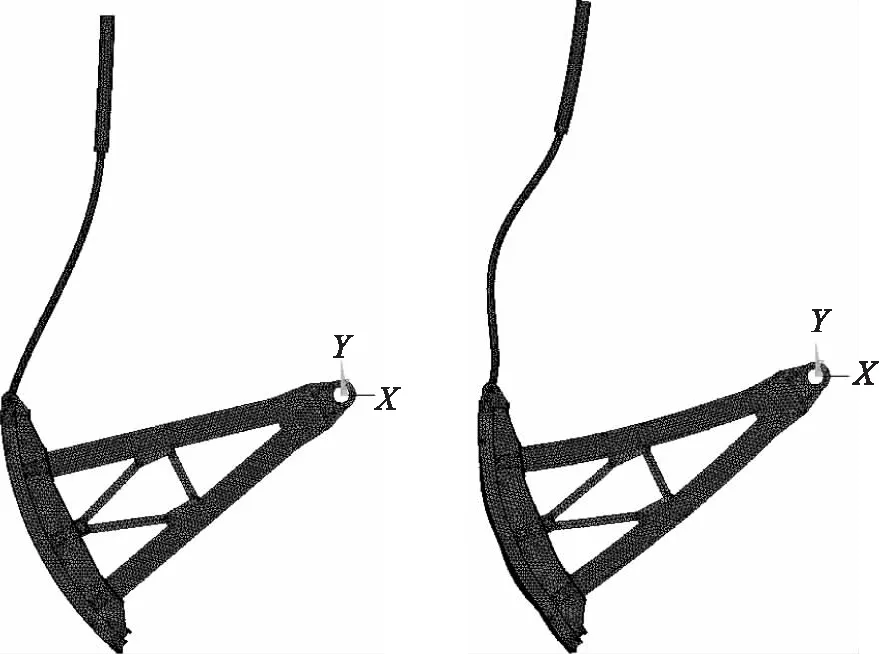
图2 闸门1阶和4阶湿模态振型
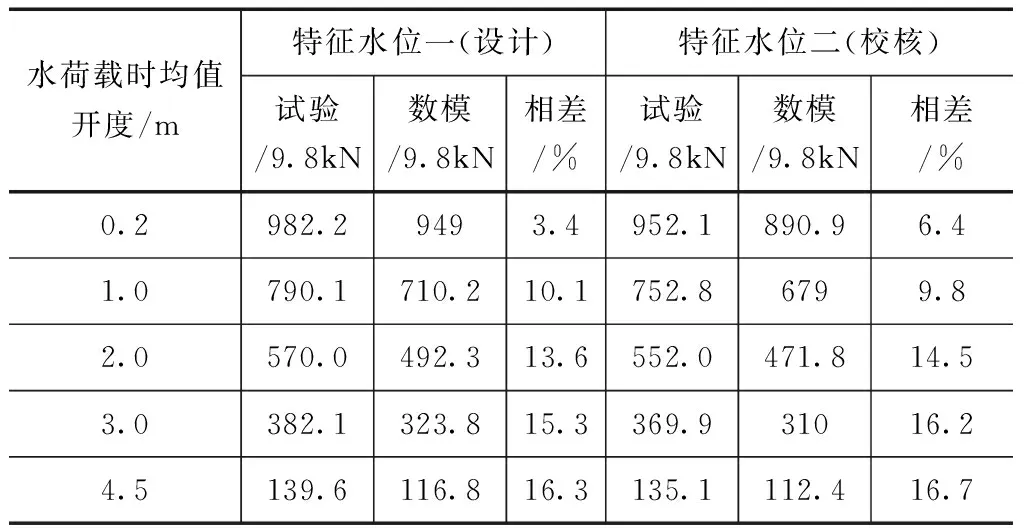
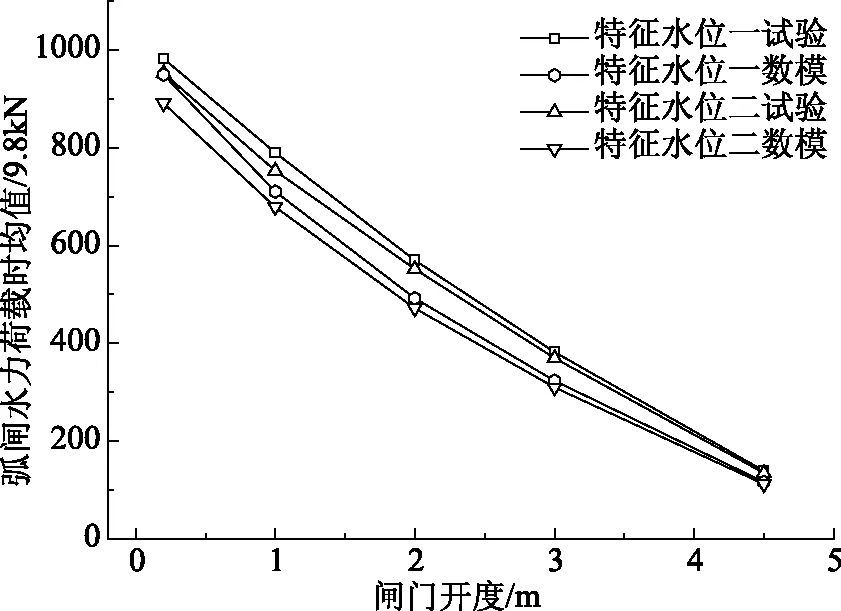
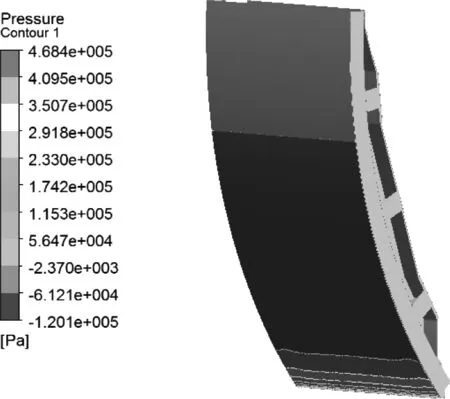
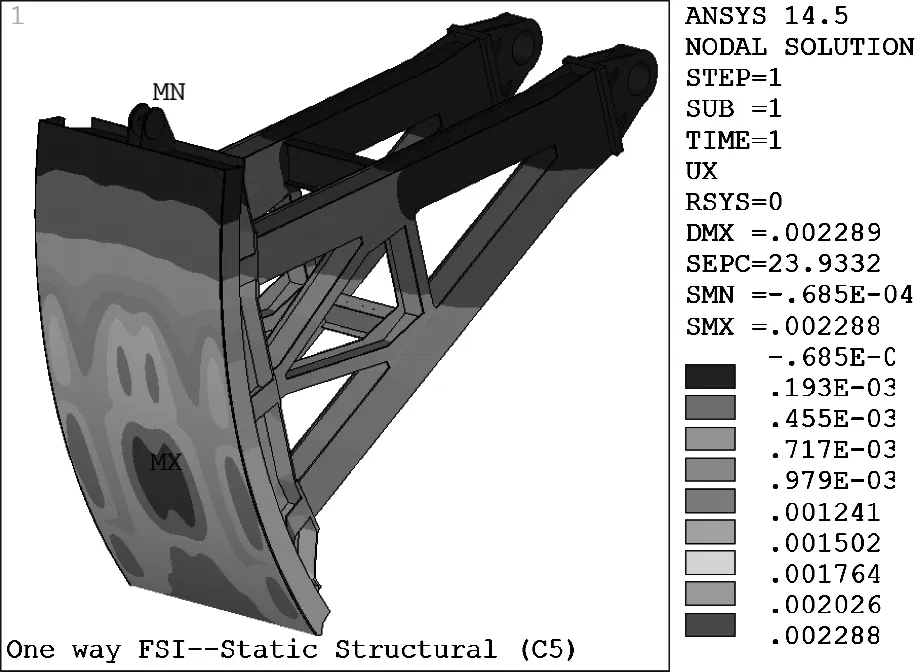
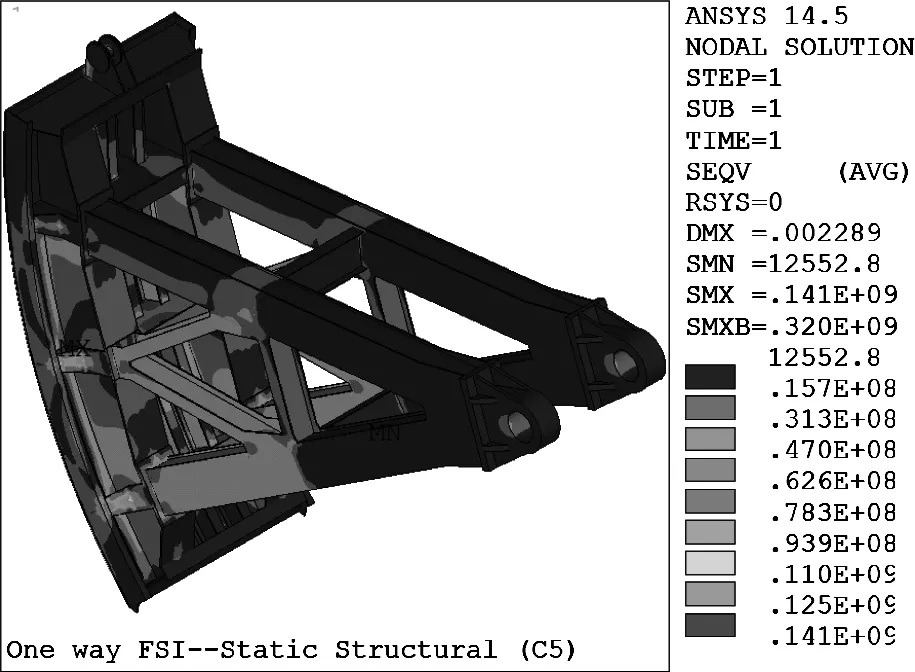
结合计算成果可知,由于闸门系统刚度分布不均匀,即抗弯刚度I杆 本次以不将结构域位移反馈到流场的单向流固耦合法进行数值分析,求得不同开度下闸门面板水力荷载与分布,以及闸门结构位移与应力等响应参数。 (1)湍流模型选择 对于泄流工况下的三维非定常流动,可采用雷诺时均法和大涡模拟方法求解N-S方程组。大涡模拟以直接数值模拟法求解大尺度运动,小尺度脉动对大尺度涡的作用则通过模型体现,精度虽较高而迭代计算代价巨大。基于重组化群理论的RNGκ-ε湍流模型考虑了漩涡对湍流的影响和平均应变率对耗散率的影响,具有较好的模拟精度和适用性,故本次分析采用该模型,湍动能和耗散率的控制方程如下[11]。 (7) (8) (9) 式中,模型常数C1ε=1.42,C2ε=0.68,η0=4.38,β=0.012,αk=αε≈1.393。 (2)单向耦合模型 基于Workbench平台下流体分析模块CFX和结构分析模块ANSYS Mechanical,建立不同工况下放空底孔流体域和弧形闸门结构域模型。利用ICEM完成流场非结构化网格划分,生成104.0万个节点、541.6万个单元,网格平均畸变度控制为0.2;同时以六面体单元为主的划分方式对闸门结构进行离散,生成67.8万个节点、18.0万个单元,网格平均畸变度控制在0.5。以CCL语言分别设置相应工况的压力进口边界和压力出口边界,上、下游顶部为开敞边界,弧形闸门和水流接触面设置为FSI流固耦合边界,其余边界为无滑移固定边界。单向流固耦合模型如图3所示。 图3 流体域与结构域计算模型 (3)耦合求解计算 本次选取闸门在设计特征水位(上游水位162.2m、下游水位114.80m)和校核特征水位(上游水位164.4m、下游水位117.20m)下各5种开度作为计算工况。采用RNGκ-ε湍流模型,以VOF多相流模型追踪自由水面,N-S方程组以守恒型式的有限体积法离散,离散格式为基于迎风格式的高精度格式,非稳定项离散格式为二阶向后欧拉,采用多网格耦合隐式求解,设置模拟总时间20s,时间步长0.02s,水压力荷载数据传递通过多场求解器MFX中conservative插值方法实现无缝对接。 结构域中求解分析采用Rayleigh阻尼,即认为各阶控制频率的阻尼比相等为0.02,阻尼系数按下式求取: (9) 式中,ξ—钢结构阻尼比0.02;ωn、ωm—2.4节中的湿模态频率,前者取基频,后者取后几阶中对结构振动贡献较大的频率,本次选取的是闸门结构的第二阶频率。 (1)水力荷载分析 作用于闸门上的流体荷载主要为面板上的水压力荷载,数值模拟可以直接获得接触面上水压力荷载及分布,并得到水压力荷载合力值。目前模型试验中流体荷载合力多是通过测试支铰力而得[12],即在闸门水力学模型的四个支臂上各安装一个力传感器,测量前进行平衡标定,测量时四个传感器同步采集数据,然后将力时间过程线进行合成和处理,进而得到由闸门面板传到支铰上的流体荷载。 本次将数值模拟得到的闸门面板水力荷载同对应工况下水力学模型试验实测支铰力结果进行整理和对比,不同开度下试验和数模水力荷载结果对比见表2、如图4所示。 表2 不同开度下试验、数模水力荷载 图4 试验与数模水力荷载对比 对比模型试验与数值模拟所得水力荷载,其随开度的变化规律一致,数值上前者稍大于后者,相对差随开度增大而增加,开度较小时相对差不超过10%,最大开度下相对差16.7%。模型试验虽在测量前对传感器进行了标定,但在动水作用下的任一时刻,支铰会受到水压力荷载与附加吊杆力的联合作用,故支铰力同闸门面板的水压力荷载有一定差别,但由于模型试验成果稍大,工程中采用偏于安全;另一方面,数值模拟中对边界和局部结构的简化处理对水压力荷载结果也存在一定影响。总体上来说,数值模拟和模型试验结果相当,将数值模拟成果进行工程应用是可行的。单向耦合数值模拟得到的闸门面板上水压力云图如图5所示。 图5 闸门面板瞬时水压力分布 (2)结构响应分析 以特征水位二、闸门开度1.0m的工况为例,选取耦合时间t=14.42s(此时流场已基本稳定),该时刻下闸门水流向位移和等效应力如图6—7所示。 图6 闸门顺水流向位移分布云图 图7 闸门等效应力分布云图 从单向流固耦合的计算结果可知,计算工况下弧形闸门最大水流向位移出现在中、下横梁与次梁所围面板区隔的中上部,最大位移2.3mm;最大等效应力出现在中横梁翼缘与边纵梁翼缘搭接处,最大应力141MPa,存在一定程度的应力集中,小于弧形闸门的容许应力。总体来说,单向流固耦合可以获取闸门结构任意关键部位的位移、应力等响应数值,可以较高效和方便的进行闸门结构分析及设计优化。 (1)考虑水体耦合作用,闸门整体绕支铰在XY平面内的振动(第4阶)受流固耦合影响较明显,该阶自振频率较干模态均有所降低,且开度越小频率降低越多,最大降幅为21%。 (2)单向耦合所得闸门面板水力荷载和模型试验测得支铰力荷载水平基本相当,最大相对差不超过17%,且与开度的变化规律一致,泄流条件下的数值模拟成果用于工程实际是可行的,模型试验成果更偏于保守和安全。 (3)ANSYS Workbench基于严格的数据插值传递,数值模拟中的流体荷载可直接耦合用于闸门结构响应分析,得到位移、应力等数值及分布,为闸门结构设计和优化提供了一种新的途径。3 单向流固耦合数值分析
3.1 耦合模型与求解设置
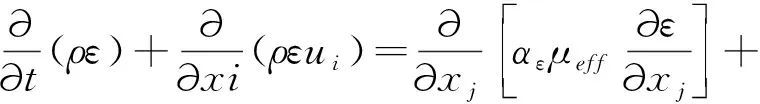
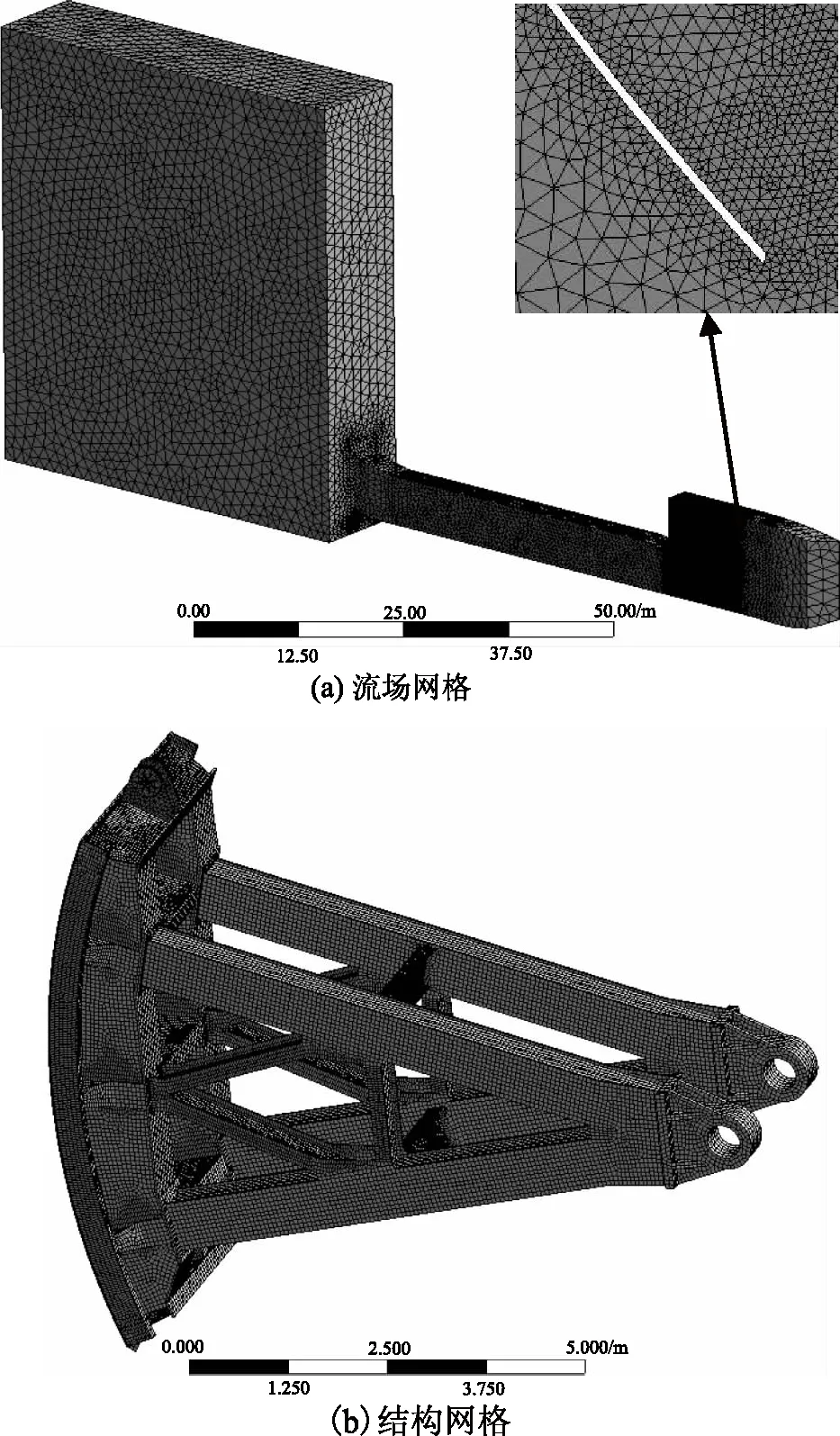
3.2 结果分析
4 结论

