基于Post Hoc平均数多重比较的桉木物性参数检测与分析
符羽栋, 杨 琳
(南京林业大学家居与工业设计学院,江苏 南京 210037)
木材是绿色、环保、可再生的生物材料,从古至今在建筑、家具、工业、农业等制品上得到了广泛的应用。但木材中的水分对木材的物理力学性能、耐候性、耐生物侵蚀性等具有极大的影响。因此,木材只有经过干燥脱水后才能更好的用于产品的制造和生产。
到目前为止,木材常规窑[1]是生产中最常用的干燥方法,其他的特种干燥,如冷冻干燥[2-4]、冷藏干燥[5]、超临界CO2干燥[6]、高频微波干燥等在生产中做有益的补充。此外,在一些特殊的场合,还需要对木材进行改性处理来提高其尺寸稳定性、耐腐蚀性、耐水性等材性特征[7-8],进而满足这些特殊的生产及使用要求。
桉木是我国种植广泛的人工林树种,为拓宽人工林桉木的应用,国内外学者做了很多研究[9-10]。综合分析材料[11-14]、市场[15]、加工制造[16]等方面的因素,提高桉木的应用范围和产品的附加值应该更加注重文化传承[17]、营销创新[18],产品设计等要在理念及方法[19-24]上进行创新和融合。
为了促进桉木的加工利用,研究干燥及加工过程的含水率、密度及干缩率等物性参数非常必要。本研究以尾巨桉为试验材料,测量其气干及吸水过程的含水率及对应于特殊含水率阶段的密度和干缩率,并利用Spss软件研究测试试件的数量对测量值的影响,为桉木干燥及热处理等加工提供实践参考。
1 材料与方法
1.1 试验材料
广西柳州产速生林尾巨桉(Eucalyptusurophylla×E.grandis)。原木采伐后用塑料薄膜包裹密封后运输至南京林业大学。在实验室将原木加工成1 000 mm(L)×20 mm(T)×20 mm(R)弦径分明的木条,再次用塑料薄膜包裹密封后放入冰柜冷藏。实验开始前随机选取一根木条,将木条端部截掉50 mm长木块后,依次截取20 mm(L)×20 mm(T)×20 mm(R)小木块,并编号1、2、3…15,测量并记录其质量和尺寸。小木块用于后续含水率、密度及干缩率的测量。
1.2 试验设备
鼓风干燥箱(DHG-905386-Ⅲ上海新苗医疗器械制造有限公司),用于烘干木材获取木材的绝干质量;电子天平(FA2004,精度0.001 g,上海精密仪器有限公司),用于测量试验过程木材的质量;数显游标卡尺(日本三丰,精度0.01 mm),用于测量实验过程木材弦、径及长度方向的尺寸。
1.3 实验方法
本试验以规格20 mm(L)×20 mm(T)×20 mm(R)小木块为试件,合计15块。首先对其进行实验室气干试验,干燥过程定期测量其质量和尺寸,直至其含水率达到平衡;然后烘干所有试件至绝干,再次测量其绝干质量和尺寸;最后把所有试件放置在烧杯内进行吸水试验,吸水过程定期测量其质量和尺寸,直至其含水率达到饱和。
整个实验过程需要测量的木材物性参数包括:(1)含水率(初、饱水、气干);(2)密度(饱水、生材、气干、绝干、基本);(3)干缩率(气干、绝干)。
1.3.1 含水率测量
木材各个阶段(初始、气干、饱水)的含水率参照GB/T 1931-2009,按公式(1)进行测量。
MC=(m-m0)/m0×100%
(1)
式中:MC为初始、气干及吸水过程含水率(%);m为初始、气干及吸水过程质量(g);m0为试件绝干质量(g)。
1.3.2 密度测量
木材各个阶段(饱水、生材、气干、绝干、基本)的密度按公式(2)进行测量。
ρ=m/v
(2)
式中:ρ为密度(饱水、生材、气干、绝干、基本),g/cm3;m为质量(饱水、生材、气干、绝干、基本),g;v为体积(饱水、生材、气干、绝干、基本),cm3。
1.3.3 干缩率测量
木材各个阶段(饱水、生材、气干、绝干、基本)的干缩率按公式(3)进行测量。
Y=(L1-L0)/L0×100%
(9)
式中:Y为干缩率(%);L1为湿材尺寸(mm);L0为气干或绝干尺寸(mm)。
1.3.4 数据分析
利用Spss对根据不同试件数量测量的物性参数的平均值进行比较分析。首先利用One-Way Anova可以对数据进行方差齐性的检验,检验各组的方差是否满足方差齐性。然后,利用One-Way Anova的下的Post Hoc中的Duncan对各组的平均数进行多重比较分析,检验各组数据间是否存在显著性差异。
2 结果与分析
2.1 试件数量与含水率测量结果
试件数量对各阶段含水率测量的影响如图1所示。处于不同阶段的木材其含水率差异很大,木材吸水达到饱和后其含水率最高,为151%左右,其次是木材刚锯切时的初始含水率,为80%左右,最低的是木材在实验室达到气干后的含水率,10%左右。由图1可以看出,只有木材初含水率的平均值及其误差棒波动较大。但是,对于饱水含水率和气干含水率,试件数量对测量的平均值及其误差棒都影响很小。
Post Hoc中的Duncan功能,可以对各组的平均值进行多重比较分析,检验各组数据间是否存在显著性差异。基于Duncan的含水率平均值多重比较如图2所示,对于饱水含水率、初含水率及气干含水率,不同试件数测得的含水率(即不同组之间)的对应概率p都大于0.05,统计上没有显著差异。即使对图1中的初含水率,看上去各组之间的平均值不同,但是对应的概率p值为0.100大于0.05,各组平均值之间无显著差异。结果表明,当测试试件超过3个时,试件数量对饱水含水率、初含水率及气干含水率的测量无显著影响。
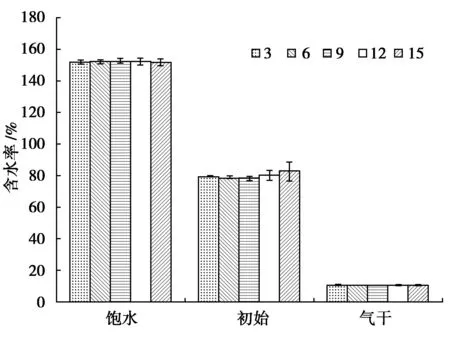
图1 试件数量对各阶段含水率测量的影响
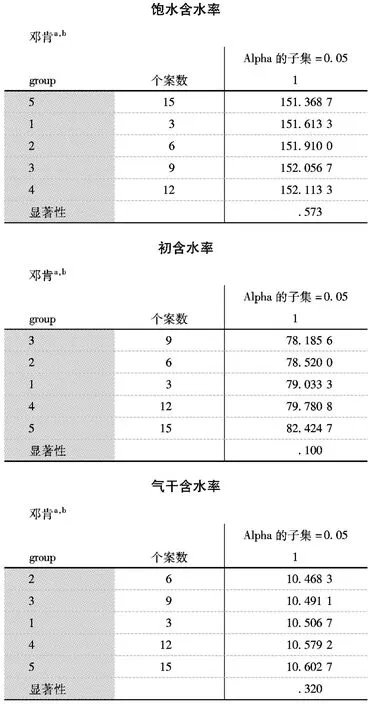
图2 基于Duncan的含水率平均值多重比较
2.2 试件数量与密度测量结果
试件数量对各含水率阶段密度测量的影响如图3所示。由图3可知,木材各阶段的密度随含水率的变化而不同,其中饱水密度最大,在1.12 g/cm3左右,其次是生材密度,在0.80 g/cm3左右,然后依次是气干密度、绝干密度,基本密度最小。
对比图1,可以看出图3中的生材密度测量值波动最大。这表明木材锯截时其各个部位的含水率有差异,进而导致木材在密度上测量值波动较大。基于Duncan的密度平均值多重比较如图4所示。结合图4的统计对比分析可知,基于不同试件数量的各组密度测量值的差异在P<0.05的条件下不显著,即试件数量对密度的测量影响不显著。
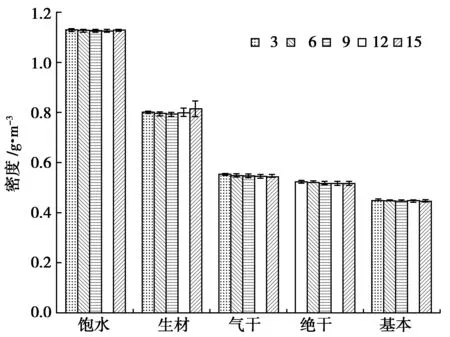
图3 试件数量对密度测量的影响
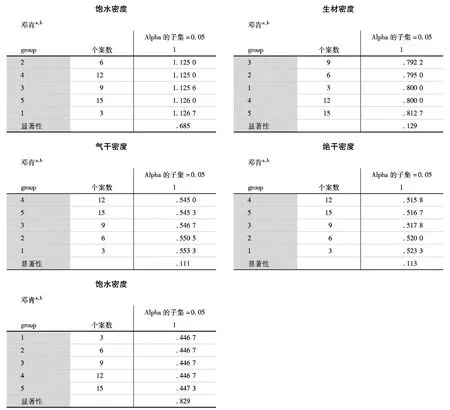
图4 基于Duncan的密度平均值多重比较
2.3 试件数量与干缩率测量结果
试件数量对各含水率阶段弦向干缩率测量的影响如图5所示。由图5可知,桉木的绝干干缩率大于气干。对比图1的含水率和图3的密度,试件数量对干缩率测量的影响波动较大,无论是气干还是绝干干缩率。当试件数量大于9个时,测量值的误差棒变大,表明测量数据波动变大。但试件数量从9个到15个的测量数据的波动几乎相等,可以从误差棒的大小可以看出。
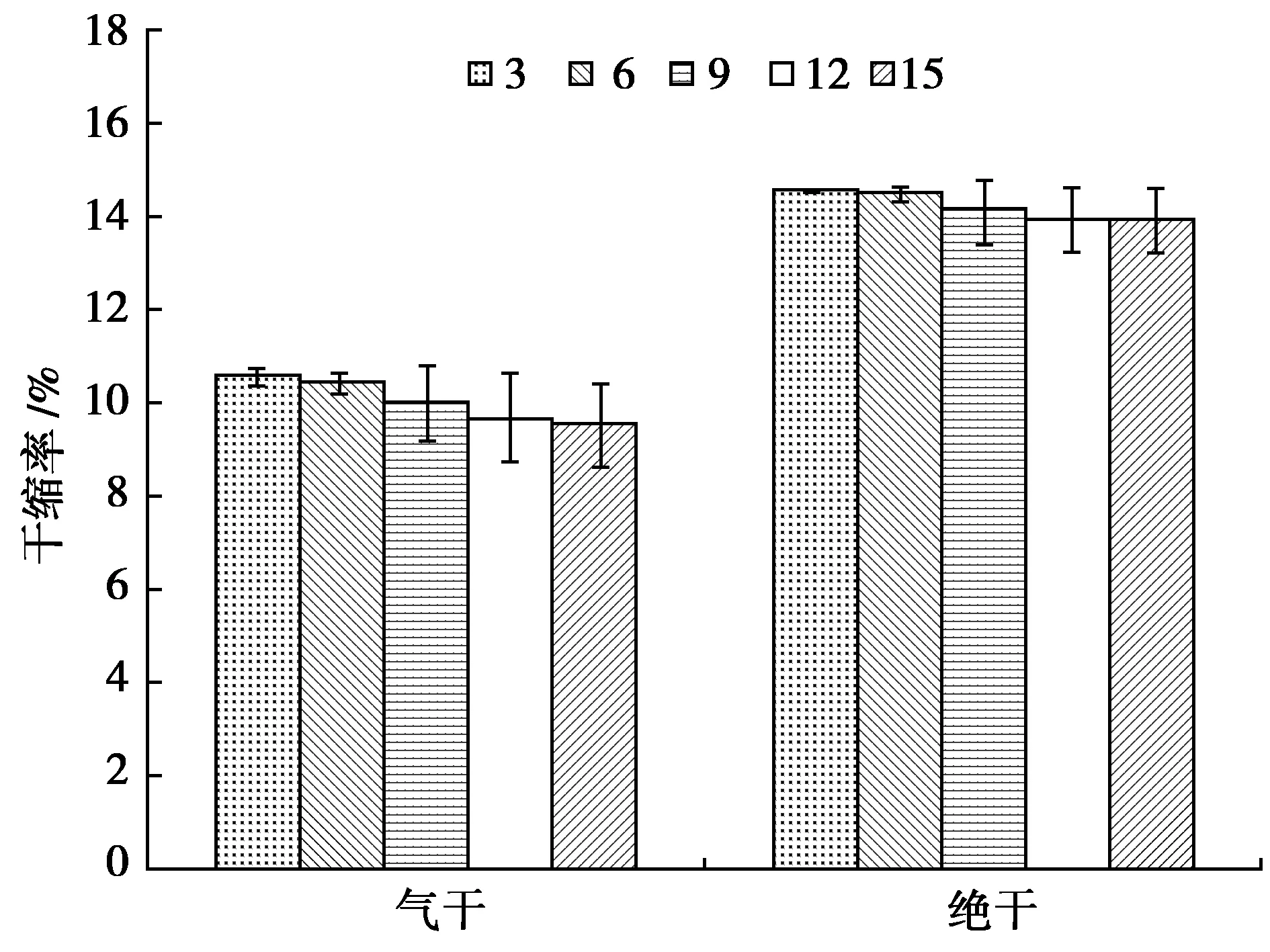
图5 试件数量对弦向干缩率测量的影响
基于Duncan的弦向干缩率平均值多重比较如图6所示。尽管随着测试试件的数量增加,数据波动变大,但是通过Post Hoc的Duncan功能方差分析,可以看出无论对于气干干缩率还是绝干干缩率,各组试件测量值之间没有显著差异。测试试件大于3个时,试件的数量对弦向干缩率的测量没有显著影响。
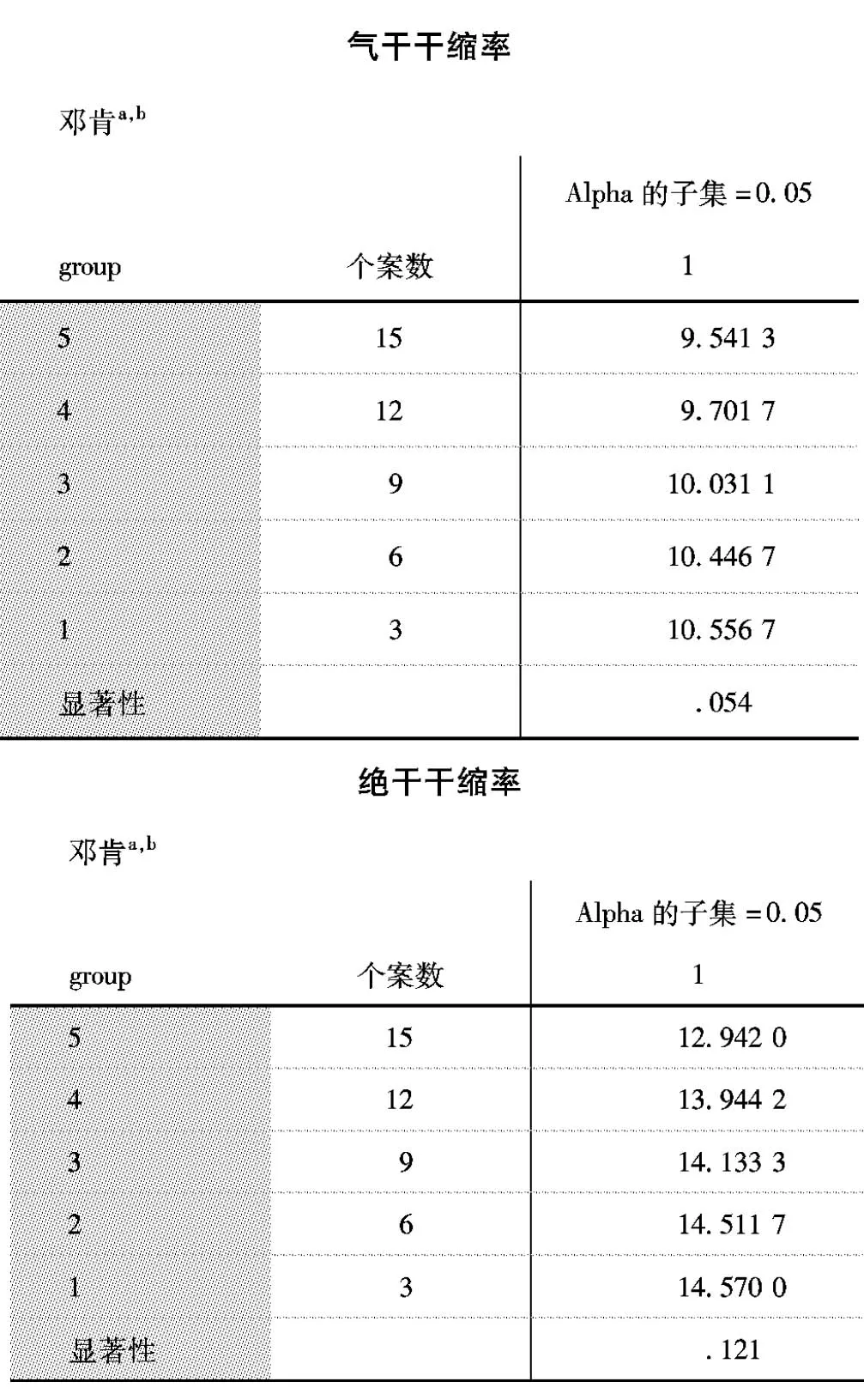
图6 基于Duncan的弦向干缩率平均值多重比较
3 结论
(1)试件初始状态的含水率及密度值随测量试件的数量波动较大,表明这两项参数在木材中分布不均。
(2)试件的气干和绝干弦向干缩率随测量试件的数量增加呈现波动,表明木材的干缩率测量波动较大。
(3)Post Hoc中Duncan的统计对比分析表明,当测量试件数量超过3个时,试件的数量对含水率、密度及干缩率的测量没有显著影响。

