正交各向异性声源膜板的自由振动特性分析
王久法
(宜昌测试技术研究所,湖北 宜昌 443099)
发声器可模拟舰船或潜艇的辐射噪声,应用于反潜战、水雷战等军事领域以及工程领域中,也可发出低频声场,应用于海底资源勘探等工程领域中。声源膜板作为发声器的重要组成部分,其振动特性对发声器的性能有着重要的影响。
正交各向异性材料由于在各个方向上具有不同力学性质,通过改变不同方向的性能参数,可以灵活控制结构的振动特性,从而产生不同的辐射噪声,实现不同噪声谱的模拟,因此,正交各向异性材料越来越广泛的应用于发声器中。
为了分析正交各向异性材料的振动特性,近年来,许多学者进行了大量研究,取得了一系列成果。如Gorman[1]使用叠加法,Hurlebaus等[2]采用Galerkin原理,Xing等[3-4]采用分离变量法,Jafari等[5]采用微分求积法分析了正交各向异性薄板结构的振动特性。不过,这些研究均基于Kirchhoff理论,其适用范围有限,当结构厚度较大时,该理论得到的计算结果与真实情况间会产生较大的偏差,为了提高计算准确性,Liew等[6-11]采用Reyleigh-Ritz法、分离变量法、谱有限元法等方法开展中厚板结构的振动特性分析。
这些研究在建立边界约束方程时,边界条件均假定为固支、简支和自由等经典条件,而正交各向异性声源膜板在实际使用时,其边界条件并非仅仅局限于这几种经典边界条件,还存在着均匀弹性支撑等复杂的边界条件,建立正交各向异性声源膜板在弹性支撑下的振动模型具有重要的意义。近年来,Li等[12-14]提出一种改进的Fourier级数方法,开展了弹性边界条件下的板梁结构的振动特性分析。Du等[15-17]将该方法进一步拓展应用,结合Hamilton原理,实现了中厚板、层合板等结构在弹性边界条件下的振动特性分析。
本文采用改进Fourier级数的方法,将正交各向异性声源膜板的振动位移函数表示为标准的二维Fourier余弦级数和辅助Fourier级数之和的形式,通过辅助级数的引入,实现了振动位移函数在整个板的求解域内展开时都有连续的一阶导数。基于Mindlin理论,推导出正交各向异性声源膜板在任意边界条件下的振动矩阵方程,不同边界条件的振动特性可通过求解该矩阵方程而得到。
1 控制微分方程求解
正交各向异性声源膜板的模型,如图1所示,声源膜板结构的四个边界处分别均匀地布置横向位移弹簧、旋转弹簧和扭转弹簧,通过改变刚度值,实现对任意弹性边界条件的模拟。

图1 弹性边界条件下声源膜板结构示意图
经典边界条件均可通过对弹簧的刚度值进行相应的设置而得到。当所有弹簧刚度值均为零时,可实现自由边界条件的模拟;横向位移和扭转约束弹簧刚度值为无穷大,当旋转约束弹簧刚度值为零时,可实现简支边界条件的模拟;当所有的弹簧刚度值均为无穷大时,可实现固支边界条件的模拟,文中无穷大取为107×D0。
根据Mindlin理论,正交各向异性声源膜板结构自由振动的控制方程为
(1)
式中:D1,D2,D3,D12,D6,G4,G5为正交各向异性声源膜板的材料参数,可参考Liew的研究进行计算。当其为单层板结构时,D1=E1h3/[12(1-v1v2)],D2=E2h3/[12(1-v1v2)],D3=D12+D6,D12=v1D1=v2D2,D6=G12h3/12,G4=kG23h,G5=kG13h,J=h3/12;w为挠度;ρ为密度;h为厚度;k为剪切系数;E1,E2,v1,v2,G12,G13和G23为单层板的弹性常数;ω为角频率。
为了解决振动位移函数在边界处的不连续问题,本文采用改进Fourier级数方法,将正交各异性声源膜板结构的横向位移函数和转角函数通过沿x轴和y轴方向的两个分量来描述
(4)
(5)
(6)
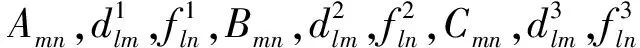
(7)
(8)
与y相关的辅助函数可以将式(7)、式(8)中的a和x分别用b和y进行替换得到。从式(4)~式(6)可以看出,振动位移和转角函数展开时除了标准的二维Fourier级数,还增加了四项辅助的单Fourier级数。通过辅助项,可有效解决振动位移和转角函数关于x和y的一阶偏导在边界处的潜在不连续性问题。因此,改进的Fourier级数解可以适用于任意的弹性边界条件,同时也能改善级数的收敛性。
将式(4)~式(6)代入控制式(1)中,并将所有的辅助级数及其导数均展开为Fourier余弦级数,并利用方程左右两端余弦项系数相等有
(9)
式中:m=0,1,2,…;n=0,1,2,…;辅助级数及其导数的Fourier展开为
(10)
(11)
同理,将式(4)~式(6)代入控制方程式(2)和式(3)中并展开为Fourier余弦级数。将当所有级数展开在数值计算过程中均截断于m=M和n=N,式(1)~式(3)可以写为
(BA+CP)+ρhω2(EA+FP)=0
(12)

2 弹性约束边界条件
弹性约束边界条件可写为

(13)
(14)
(15)

(16)
(17)
(18)

(19)
(20)
(21)

(22)
(23)
(24)
式中:kx0,Kx0和Kyx0(kxa,Kxa和Kyxa)分别为x=0(x=a)处横向位移、旋转和扭转约束弹簧刚度;ky0,Ky0和Kxy0(kyb,Kyb和Kxyb)分别为y=0(y=b)处横向位移、旋转和扭转约束弹簧刚度。
将式(4)~式(6)代入式(13)~式(18)中,并将辅助级数展开Fourier级数,由方程两端余弦项系数相等有
(25)
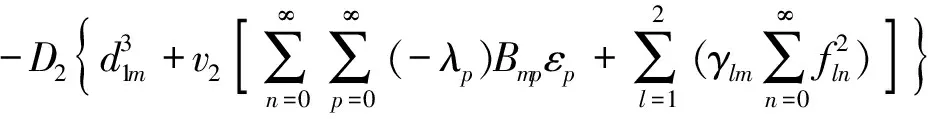

式中,m=0,1,2,…。
(28)

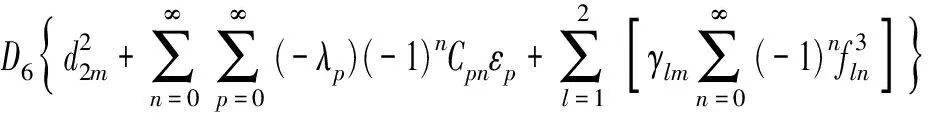
式中,n=0,1,2,…。
同理,将式(4)~式(6)代入式(19)~式(24)中可得另外六个方程式。当级数的截断数取为m=M和n=N时,约束方程可写成矩阵表达示为
HP=QA
(31)
将式(31)代入式(12)中,可得到最终的系统方程为
(K-ρhω2M)A=0
(32)
式中:K=(B+CH-1Q)/D1;M=(E+FH-1Q)。
正交各向异性声源膜板的振动频率以及振型均可通过求解这一标准矩阵方程的特征值和特征向量得到,其中,特征向量为所对应结构模态形状分布的Fourier系数。
3 数值结果与讨论
本文考虑的正交各向异性声源膜板为复合材料层合板,由多层等厚的单元板复合而成。单元板的材料性能参数为Ex/Ey=40,G12=3/5Ey,G23=1/2Ey,G13=3/5Ey,vy=1/4,vx=0.006 25;剪切修正系数为k=π2/12。文中:C为固支边界条件;F为自由边界条件;S为简支边界条件。假设某边界条件为FSCC,其表示沿边界x=0,y=0,x=a和y=b的边界条件分别为自由、简支、固支和固支。
在求解式(32)时,M和N取值越大,计算结果越精确,当M和N趋于无穷大时得到精确解。在实际的工程应用中,M和N的值越大,其计算时间和成本越大,因此,快速收敛成为该方法是否适用的重要参考指标。为了检验收敛性,表1给出了正交各向异性声源膜板在不同截断数时的计算结果,其中,声源膜板为三层板结构0°/90°/0°,声源膜板的长宽比a/b=1,厚度比b/h=10,边界条件为SSFF。从表1中可以看出,M和N的值超过10时,计算结果几乎就不再变化,M=N=3和M=N=16时得到的前八阶无量纲固有频率的最大偏差为1.38%,即本方法具有较好的收敛性,当截断数取较小的值时就能得到比较精确的结果。
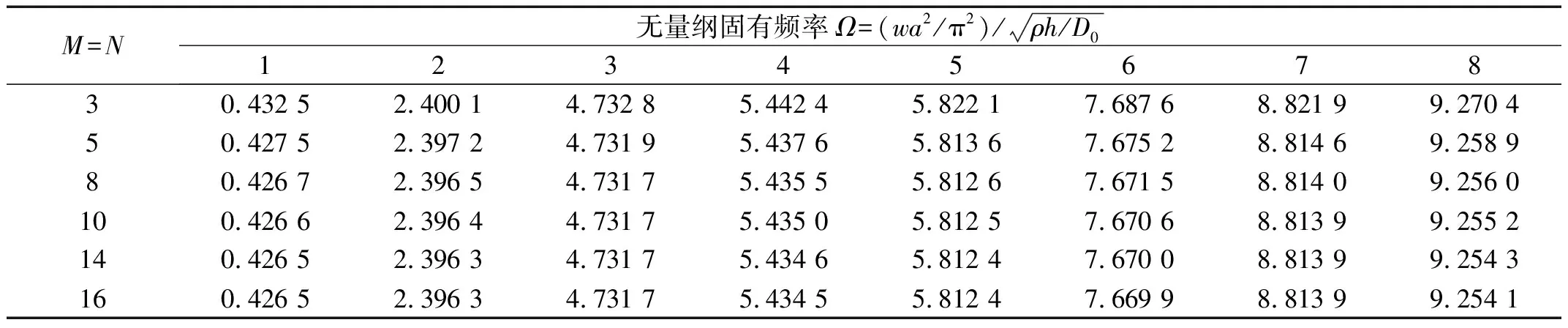
表1 声源膜板振动方程的收敛性
通过求解式(32)可得到结构在任意边界条件下的模态信息,表2给出了不同厚度比和经典边界条件下正交各向异性声源膜板的前六阶无量纲振动频率参数Ω=(ωa2/π2)(ρh/D0)1/2,其中,声源膜板为三层板结构0°/90°/0°,D0=Eyh3/[12(1-vxvy)],两个方向的振动位移函数展开时均采用相同的截断数,取值为M=N=12。为了验证本文方法的准确性,表2中也给出了Liew采用Ritz法以及Liu等研究中采用分离变量法得到的计算结果,通过比较可知,本文方法得到的结果与其他方法得到的结果吻合良好,最大偏差不超过0.5%,即本文方法适用于各种经典边界条件的振动问题的求解。
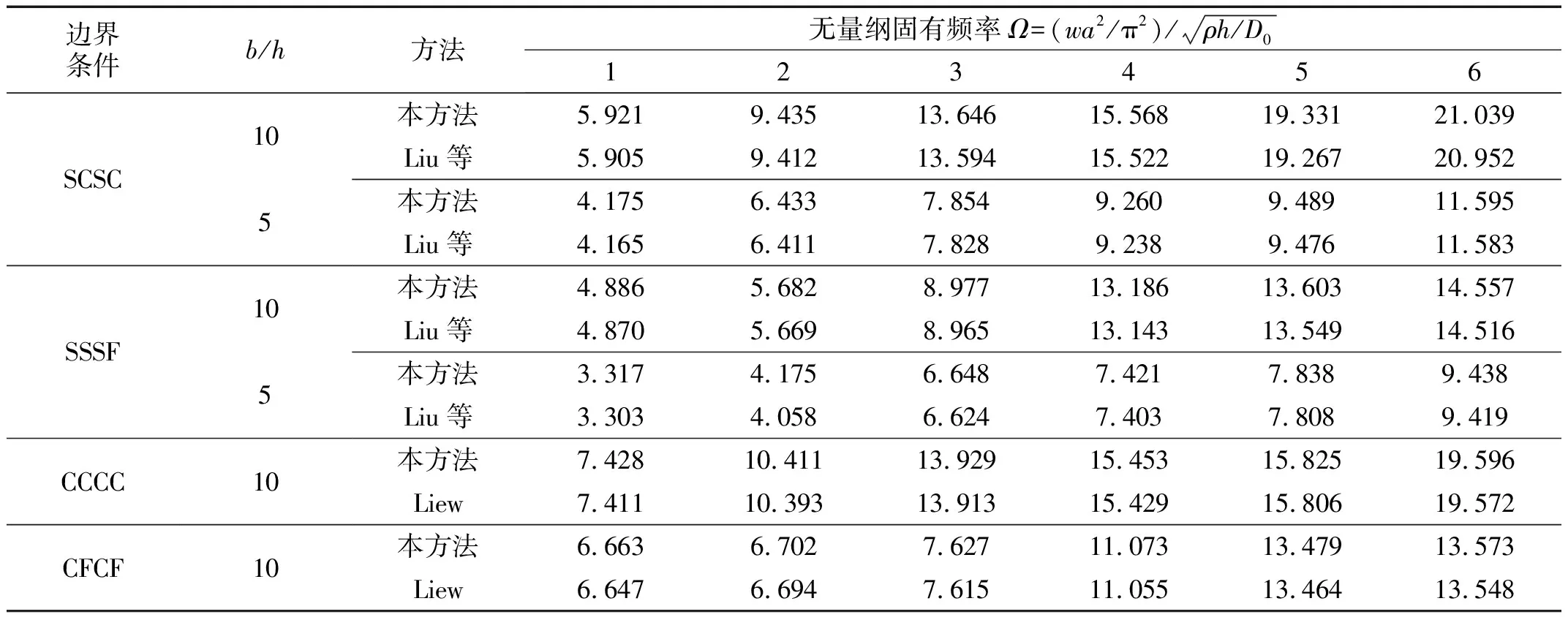
表2 经典边界条件的声源膜板的频率参数
表3分别给出反对称角铺设以及正规对称正交铺设四边简支正交各向异性膜板在不同的厚度比条件下的基频,同时,表中也给出了文献[18-19]采用高阶剪切理论得到的结果。45°/-45°/45°/-45°表示正交各向异性膜板由4层单层板构成,第1层和第3层的主方向的夹角为45°,第2层和第3层为-45°,从计算结果可知,本文方法得到的结果与高阶剪切理论得到的结果偏差不超过1%,特别是当厚度比不超过0.1时,两种方法的偏差不超过0.5%。

表3 四边简支正交各向异性膜板的基频
本方法采用约束弹簧来模拟边界条件,通过将其作为振动方程中的一个参数,使边界条件的问题转化为弹簧刚度参数设置的问题,从而便于研究边界条件对振动特性的影响。图2给出了长宽比a/b=1,厚度比b/h=5的声源膜板在不同弹性支撑刚度下的前十阶无量纲振动频率曲线。其中,板结构四边上的横向位移约束弹簧刚度值和扭转约束弹簧刚度值都为无穷大,旋转移约束弹簧刚度值为10k×D1。图中曲线k(k=1,2,…,7)表示为旋转约束弹簧刚度值都为10k×D1下的计算结果。从图2中可以看出,当k≤4时,弹簧刚度值对声源膜板结构的振动频率产生极为明显的影响,随着弹簧刚度值的增加,矩形板的频率也随之增大。因此,在发声器工作过程中,可通过改变声源膜板的边界条件,实现不同噪声谱的模拟。同时,从图2中也可看出,当k≥5时,曲线几乎不在变化,频率值变为边界条件为CCCC下的结果。从这里也能看出,本文看中刚度值为107×D1近似为无穷大是合适的。

图2 弹性边界条件下板的振动频率
4 结 论
本文采用改进Fourier级数方法,将横向振动位移函数和转角函数表示为标准的二维Fourier余弦级数和辅助级数的线性叠加,建立了正交各向异性声源膜板的在任意边界条件下通用振动模型,声源膜板的固有频率和振型等均可通过求解该矩阵方程得到。声源膜板的边界条件采用横向位移约束弹簧、旋转约束弹簧和扭转约束弹簧来模拟,不同边界条件通过设置相应的边界弹簧刚度值来实现。最后进行了数值仿真分析,并与其他文献的结果进行了比较,验证了本方法的快速收敛性和准确性。

