一种新的轴承寿命预测特征评价指标构建与验证

曾大懿，蒋雨良，邹益胜，张笑璐，李海浪

(西南交通大学 机械工程学院，成都 610031)

滚动轴承是机械设备中关键的零部件之一[1]，其可靠性直接影响了设备的性能，所以对滚动轴承的剩余使用寿命(remaining useful life, RUL)进行预测是十分必要的[2-5]。采集滚动轴承的振动信号，并对信号进行有效分析，是目前研究滚动轴承RUL的主要方法。滚动轴承的振动信号中蕴含着丰富的信息，可从这些信息中获得轴承的健康状态。从振动信号中提取信息后，如何对这些信息进行量化的评价与筛选，减少信息的冗余，并使这些信息有利于提高轴承RUL的预测精度，这是一个值得研究的问题。目前，此类问题的研究方面主要有降维算法研究和评价指标研究等方面。

在降维算法研究方面，何群等[6]在研究基于多变量极限学习机的轴承寿命预测方法时，采用主成分分析对高维特征集进行降维。肖婷等[7]利用局部保持投影算法对高维特征集进行简约。Liu等[8]采用特征矩阵近似对角化对特征进行加权融合。

在评价指标研究方面，Zhang等[9]通过对原始状态监测信号的时域、频域和时频域进行处理，生成候选预测特征，并根据特征的趋势和残差定义了时间相关性、单调性和鲁棒性三种指标，同时并分别以0.2，0.5，0.3的权重对这三种指标进行加权融合，用于轴承信号特征的选择。Guo等[10]在轴承寿命预测研究时，提取了轴承信号的时域、频域和时频域特征，并根据单调性与时间相关性度量，从提取的特征集中选出认为最敏感的特征；并在将特征的综合得分归一化后，提出了0.5的筛选阈值，用于选择最佳特征子集。Wang等[11]研究一种基于长短时记忆(long short-term memory, LSTM)网络的剩余寿命预测方法时，同样提取了信号的时域、频域和时频域特征，采用了Zhang等定义的三种特征评价指标，同时认为单调性指标更加重要，并将0.4的权重赋予单调性指标，其余2个指标则平均分配剩余权重，最终以0.3，0.4，0.3的权重组合指标，综合评价特征的优劣，并将Guo等提出的0.5的筛选阈值修改为0.6。康守强等[12]在研究滚动轴承RUL预测方法时，提取了轴承信号的时域、频域和形态学特征，并提出一种自适应确定每个评价指标权重的方法。柏林等[13]在单调性与敏感性评估的基础上，对轴承信号的时域与频域特征进行评价。谷广宇等[14]使用了时间相关性、单调性、离散性和鲁棒性4个评价指标，对发动机的状态特征进行评价与筛选。刘胜兰等[15]在预测轴承寿命过程中，采集了轴承的时域、频域、IMF(intrinsic mode function)分量、希尔伯特边际谱特征和熵特征，使用时间相关性、单调性和鲁棒性3个指标来综合评价特征。

然而在现有的轴承寿命预测的特征评价研究中，均是对振动信号的时域、频域等特征进行评价与筛选，并未发现对深度学习模型提取的特征进行评价的研究。深度学习模型自动提取特征的功能能够减轻人工提取特征的繁杂，将信号特征评价方法用于评价此类特征，可以节省人力并减少人为因素的影响，并且可以提高这类特征的可解释性。因此，对深度学习模型提取的特征进行评价，具有一定的价值。

同时在特征的评价过程中，针对同一种特征在不同轴承之间存在的异同，提出了一种基于趋势一致性指标的轴承寿命预测特征筛选方法。对深度学习模型提取信号特征进行评价与筛选，并使用筛选出的特征进行轴承RUL预测。与根据经典的评价指标获得的预测结果进行对比，验证了该方法的有效性。

1 趋势一致性寿命预测特征评价指标构建

1.1 典型的三种寿命预测评价指标

在目前的评价指标研究中，时间相关性、单调性和鲁棒性指标是比较常用的指标，所以将这三种指标用于评价深度模型提取的信号特征，与趋势一致性指标对应的预测结果进行对比。

一个轴承全寿命周期的一个信号特征序列表示为X=[X(t1),X(t2),…,X(tk)]，其中X(tk)表示在tk时间点的轴承信号特征。时间序列T=(t1,t2,…,tk)，其中tk表示第k个时间点。在进行评价之前，对信号特征进行指数加权移动平滑处理，如式(1)所示。最后将特征X(tk)分解为两部分，趋势项XT(tk)和余量项XR(tk)，如式(2)所示。

XT(tk)=αX(tk)+(1-α)X(tk-1)

(1)

X(tk)=XT(tk)+XR(tk)

(2)

式中，α取值为0.9。

时间相关性、单调性和鲁棒性指标的计算公式为

Corr(X,T)=

(3)

(4)

(5)

式中：K为时间点的总个数；δ(·)为阶跃函数，其计算公式为

(6)

1.2 趋势一致性寿命预测评价指标的设计思路

时间相关性、单调性和鲁棒性3个指标对于轴承信号特征的量化评价与优劣筛选起到了积极的作用，但是在预测时，将筛选出的特征一起输入轴承寿命预测模型，同一特征在不同轴承之间趋势上的一致性会对轴承寿命预测产生影响，而这三种经典的特征评价指标并没有直接考虑这种趋势一致性。

在时间方向上，同一种信号特征应在不同轴承之间存在趋势上的一致性；而参与轴承寿命预测的特征，其一致性程度高低应当会对轴承的寿命预测结果影响，一致性程度越高，预测结果亦越高，反之，则越低。为了对这种趋势一致性进行评价，并筛选出趋势一致性程度较高的特征用于预测轴承寿命，并提高预测精度，设计了一种新的计算方法，借助相关性计算公式，计算同一特征在不同轴承之间存在的趋势一致性，提出了趋势一致性寿命预测评价指标。

然而不同轴承之间的寿命分布具有很大的离散特性，这导致了不同轴承同一特征之间的时间长度与数值范围都有很大差异。运用相关性计算公式，无法直接对不经处理的特征进行计算。所以在计算趋势一致性指标时，首先应采用某些方法将不同轴承的同一特征压缩至具有相同长度与宽度的矩形框内。特征A与特征B具有不同时间长度a和b，以及不同的数值范围x和y，如图1所示。通过归一化与降采样等处理，在不改变特征在整个轴承寿命周期中的变化规律的前提下，将2个特征压缩至具有相同的时间长度c与相同的数值范围z矩形框中。在这个矩形框内，可以方便地描述特征在形状上或变化趋势上的一致性。

图1 特征处理思路

1.3 趋势一致性寿命预测评价指标的构建方法

首先对提取的特征进行平滑处理，其次利用归一化和降采样的方法对特征进行压缩处理，再运用相关性计算公式，计算特征之间的相关性，然后对计算出的一组相关性值取均值处理，最后获得趋势一致性指标的得分。

趋势一致性指标的主要计算过程如下：

m=K/s

(7)

G(f)={R[(f+1)×m]-R(f×m)+1}

(8)

(9)

(10)

步骤3对步骤2计算出的结果进行取均值处理，获得得分Qr，计算过程如式(11)所示。

(11)

由相关性公式的原理可知：计算出的均值符合范围在0～1的要求，所以第r个特征序列的趋势一致性指标最终得分为Qr；并且得分Qr越接近1，同一特征在不同的轴承上的趋势表现越一致。利用这种特征进行预测，应当有利于获得更优的预测精度。

2 趋势一致性指标的验证方法

2.1 验证流程

基于趋势一致性指标的轴承寿命预测特征筛选方法的验证过程，主要有以下4个步骤：

步骤1数据预处理。首先对每个时间点的原始振动信号进行快速傅里叶变换，将其转换为频域信号，并按照一定规则划分训练集与测试集。

步骤2提取特征。采用无监督的深度学习模型-卷积自编码网络模型构建特征提取模型；根据输入数据的大小与需要提取的特征数量，设置网络的形状参数；使用步骤1划分好的训练集，对特征提取网络进行训练。训练完成后，将训练集与测试集同时输入网络，获得对应的特征集。

步骤3评价与筛选特征。按照指标评价步骤，使用趋势一致性指标对训练集的特征进行指标评价；根据指标得分的高低，提取出趋势一致性指标认为的优质特征对应的序号；根据该序号从训练集和测试集对应的特征集中，选出序号对应的优质特征，最后组合成训练集与测试集的优质特征集。

步骤4预测RUL。采用多层LSTM网络模型作为预测模型；使用训练集的优质特征集与处理后的寿命标签对该网络进行训练；训练完成后，输入测试集的优质特征集，获得模型的预测值。

该方法的验证流程图如图2所示。

图2 验证流程图

2.2 特征提取模型

用于特征提取的深度学习网络模型是采用无监督学习方式的卷积自编码网络[16]。采用的卷积自编码网络模型主要由三层一维卷积层与三层一维反卷积层构成。网络结构如图3所示。

图3 提取特征的网络模型

2.3 轴承RUL预测模型

LSTM网络具有长时记忆的能力，适合用于处理与时间序列相关的问题，而网络的层数增加能够提升网络的抽象表达能力，所以采用多层LSTM网络作为预测模型进行试验验证。模型结构如图4所示，该模型具有三层LSTM网络层，最后一层为全连接层，用于输出寿命预测值rh。最后对预测结果采用加权平滑方法[17]进行平滑处理。

图4 寿命预测的网络模型

模型训练时的标签采用RUL百分比标签yh，表示当前时刻的剩余寿命占总寿命的百分比，其计算公式为

(12)

式中：L为对应轴承采集数据的总次数；h为此标签对应轴承的第h次采集的数据。

3 趋势一致性指标的验证与分析

3.1 数据来源

采用的轴承数据集是IEEE PHM 2012挑战赛的公开滚动轴承数据集[18]。该轴承数据集有3个工况，共17个轴承，三种工况的轴承个数分别为7，7，3。分别命名为轴承1-1～轴承1-7、轴承2-1～轴承2-7、轴承3-1～轴承3-3。

使用该数据集的采集轴承振动信号进行试验验证，振动信号的采样频率为25.6 kHz，每隔10 s采集一次数据，采集一次的时长为0.1 s，共2 560个数据。以轴承1-3为例，该轴承总共采集了2 375次，所以总寿命时长为23 750 s，具有数据量为2 375×2 560，可用数组表示为(2 375,2 560)。分别对每个时间点采集的振动数据进行快速傅里叶变换的处理，变换为频域信号。每个时间点的数据长度变为1 280，所以轴承1-3的频域信号可用数组(2 375,1 280)表示。

3.2 模型的参数设置

以提取160个特征序列为例，并根据输入数据的长度尺寸，特征提取模型的参数设置如表1所示。

表1 特征提取模型的参数

卷积层1的网络参数为(4,11,8)，其中：第1个参数表示卷积核的个数；第2个参数表示卷积核的尺寸大小；第3个参数表示步长。设置训练次数为10 000次。

网络模型训练完成之后，使用平整层将卷积层3的输出数据扁平化为一维的数据，其长度为160。将训练集和测试集分别输入训练完成的网络模型，获得模型提取的特征，此时获得的轴承1-3的信号特征可用数组(2 375,160)表示。

根据获得的上述获得特征的尺寸，预测模型的参数设置如表2所示。设置训练次数为10 000次。

表2 寿命预测模型的参数

3.3 特征提取

在试验验证过程中，从17个轴承中任意取一个轴承作为测试集，其余16个轴承作为训练集。以轴承1-3为测试集，其余所有轴承为训练集为例，来说明该方法的有效性。

轴承1-3第1个0.1 s的原始振动信号和频域信号，分别如图5和图6所示。

图5 轴承1-3第1个0.1 s的原始信号

图6 轴承1-3第1个0.1 s的频域信号

在特征提取模型训练完成之后，获得轴承1-3的160个特征序列。随机选取2个特征序列展示特征提取的效果，选取的第1个与第160个特征序列，分别如图7和图8所示。

图7 轴承1-3的第1个特征序列

图8 轴承1-3的第160个特征序列

从图7、图8中可以看出，特征提取模型能够从测试集中提取出不同的特征。

3.4 趋势一致性指标的计算与分析

在进行特征评价时，原则上只能对提取的训练集特征进行评价，并由于文章篇幅限制，所以采用图片的方式展示训练集中轴承1-2、轴承2-2和轴承3-2的指标计算过程。以第1个特征序列为例，展示使用趋势一致指标进行计算的过程。

首先对这3个轴承的第1个特征序列进行平滑处理，得到的趋势项分别如图9～图11所示。

图9 轴承1-2 特征的趋势项

图10 轴承2-2 特征的趋势项

图11 轴承3-2特征的趋势项

经过1.3节中步骤1的归一化与降采样处理后，3个轴承的特征序列分别如图12～图14所示。

图12 轴承1-2降采样后的趋势项

图13 轴承2-2降采样后的趋势项

图14 轴承3-2降采样后的趋势项

从归一化与降采样前后两种结果的对比中可以看出，该步骤并未改变特征序列的变化趋势，达到了1.3节中步骤1的计算目的。经过1.3节中步骤2相关性计算后，所有轴承特征的相关性值排列如表3所示，结果保留3位小数。

表3 同一种特征的相关性值

根据1.3节中步骤2计算获得的结果，采用1.3节中步骤3的计算方法，对表3中数据进计算，最终获得第1个特征序列的趋势一致性指标得分为0.610。

每个轴承的特征集有160个特征序列，按照上述的过程进行计算，最终获得160个分值，如图15所示。

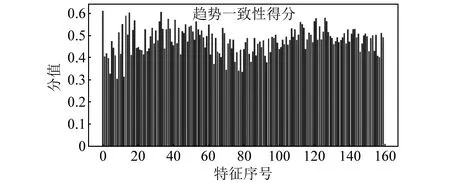
图15 全特征序列的趋势一致性得分

从图15可知，第1个特征序列的得分最高，而第8个特征序列的得分最低。为了验证得分是否合理，将轴承1-2、轴承2-2和轴承3-2的第8个特征序列降采样后的趋势项分别列出，如图16～图18所示。通过与第1个特征序列的图12～图14进行对比，可以看出趋势越相似的特征序列，指标得分越高，而趋势越不同的特征序列，指标得分越低。上述现象说明了趋势一致性指标计算方法的合理性。

图16 轴承1-2第8个特征序列降采样后的趋势项

图17 轴承2-2第8个特征序列降采样后的趋势项

图18 轴承3-2第8个特征序列降采样后的趋势项

对计算出的160个分值进行归一化处理，具体操作为：每一个分值减去最小分值，然后除以最大值。计算结果如图19所示。将筛选阈值选定为0.5，保留归一化后分值大于0.5的特征对应的序号。

图19 全特征序列的趋势一致性归一化得分

根据以上获得序号，在训练集与测试集的特征集中将序号对应的特征提取出来，这部分特征便是趋势一致性指标认为的优质特征。

从上述计算过程可以看出，特征序列的趋势一致性指标得分高低是相对的，得分高的特征序列相对于得分低的特征序列，在不同轴承上的表现更加一致。

3.5 指标得分高低对预测结果的影响

为了说明特征的得分高低对预测结果的影响，将得分大于0.5的优质特征集与小于0.5的普通特征集分别用于训练与预测。在预测试验时，选择一个轴承作为测试集，其余16个轴承作为训练集。随机以轴承1-3与轴承3-2分别作为测试集时为例，各自的优质特征集与普通特征集对应的预测结果，分别如图20和图21所示。

图20 轴承1-3两类特征集的预测结果

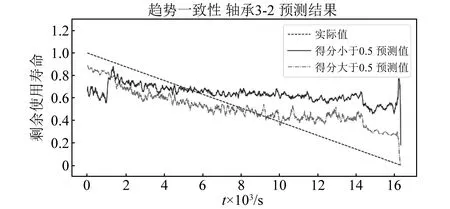
图21 轴承3-2两类特征集的预测结果

从图20和图21可知，趋势一致性指标得分高的特征对应的预测效果优于得分低的特征，说明了同一特征在不同轴承上的趋势表现越一致，有利于获得更优的预测效果。

3.6 基于不同指标评价方法的轴承RUL预测结果对比分析

使用三种典型的指标与趋势一致性指标分别用于特征的评价与筛选，将各自评价所得的优质特征集用于训练和预测，获得4组预测结果。为了更好地说明该方法的预测效果，将160个特征序列全部用于训练与预测，获得1组使用全特征序列的预测结果。

以均方根误差(root mean squared error,RMSE)作为预测误差的评价标准，计算公式为

(13)

式中，H为对应轴承预测值的总个数。

3.6.1 基于PHM 2012大赛数据集划分方式的试验结果

在PHM 2012大赛的数据集中，将轴承1-1～轴承1-2、轴承2-1～轴承2-2和轴承3-1～轴承3-2这6个轴承作为训练集，剩余11轴承作为测试集。按照这种划分方式进行试验，预测获得的RMSE如表4所示。

从表4可知，单调性指标与趋势一致性指标的预测效果稍好于全特征序列的预测结果，而时间相关性与鲁棒性指标预测效果并没有提升。其中，趋势一致性指标相对于全特征序列、时间相关性、单调性和鲁棒性指标，在RMSE的综合平均值上分别降低了5.6%，6.0%，2.5%和5.6%。

表4 试验1预测结果

3.6.2 基于留一法的试验结果

为了更直观、更全面地展示预测效果，采用留一法进行试验，将每一个轴承分别作为测试集，其余轴承作为训练集，分别在五种情况下进行预测试验。首先随机以轴承1-3与轴承3-2为例，展示其分别作为测试集时的预测结果，预测结果如表5所示。

表5 试验2预测结果

从表5可知，趋势一致性和鲁棒性指标的预测结果相对于全特征序列的预测结果，在预测精度上有较小提高；时间相关性和单调性指标的预测精度则出现了下降。

同样以RMSE作为预测误差的评价标准，所有轴承的预测误差如表6所示。并将每种情况下轴承预测误差的综合平均值列入表末。

表6 所有轴承的预测误差

为了更加清晰地展示预测效果提升，将上述17组试验的情况进行统计，如表7所示。

表7 预测结果统计

从表7的统计结果可知，在64.7%的测试样本中，趋势一致性指标的预测效果明显优于其余三种指标，说明了趋势一致性指标能够有效地从深度学习模型提取的特征集中筛选出有利于降低预测误差的优质特征集。并且相对于其余各项的预测结果，其RMSE的综合平均值分别降低了21.0%，27.6%，25.8%和19.5%，说明该特征评价方法适用于深度学习模型提取的信号特征，能够在一定程度上提高此类特征的可解释性。

4 结 论

针对如何量化评价同一种信号特征在不同轴承上表现异同的问题，提出了一种基于趋势一致性指标的筛选方法，并将该方法用于评价深度学习提取的信号特征。最后进行了轴承RUL预测的试验，得出了以下结论：

(1)提出了趋势一致性指标用于信号特征的评价与筛选。通过该指标获得的综合平均RMSE相比于三种经典指标分别降低了27.6%，25.8%，19.5%，说明了该指标能够有效得筛选出有利于降低轴承RUL预测误差的信号特征，为信号特征评价方法提供了新的思路。

(2)将信号特征评价方法用于深度学习模型提取的信号特征中，相比于不采用特征评价的情况，该指标预测的综合平均RMSE减少了21.0%，说明了该方法对此类特征的适用性，可在一定程度增加此类特征的可解释性。

考虑到使用不同的评价指标在部分轴承上取得了更优的预测效果，后续的研究将进一步对趋势一致性指标和其他指标筛选的特征进行深入的对比分析，同时也考虑将趋势一致性指标与其他指标进行融合。