并列三方柱气动特性的试验研究
刘小兵,于文文,吴倩云,陶 韬,杨 群
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;2.河北省风工程和风能利用工程技术创新中心,石家庄 050043;3.石家庄铁道大学 土木工程学院,石家庄 050043)
多方柱结构在桥墩、桥塔、高层建筑群等实际土木工程中较多存在。由于间距不大,多方柱结构之间存在气动干扰。与单方柱结构相比,在某些特定的情况下,多方柱结构的风荷载可能会被放大,风振性能可能会变差。准确掌握多方柱结构的气动特性对于实际土木工程结构的抗风设计具有重要意义。
相对来流呈并列布置是多方柱结构的一种典型布置形式,其气动特性引起了国内外众多学者的关注,其中以并列双方柱的研究最广泛。Kondo[1]通过三维数值计算的方法发现,并列双方柱的气动力特性与方柱之间的距离有关,间距较小时,2个方柱的阻力不同。陈素琴等[2-3]的数值模拟研究表明,并列双方柱在小间距时由于偏流现象的存在,气动力不等。靳遵龙等[4]开展的数值模拟研究发现,并列双方柱中心间距为3倍方柱边长时,绕流方柱的涡流影响最明显。Alam等[5]通过多种试验方法,将并列双方柱的流动特征分为四类,并分析了不同流动状态下的气动特性。Han等[6]和Yen等[7]则分别通过数值计算和烟线的方法,将并列双方柱的尾流分为三类。魏英杰等[8]开展的大涡模拟发现,并列双方柱的中心间距为1.5倍方柱边长时,在对称边界条件下,绕流运动参量的时域过程不对称,频域过程对称。王小华等[9]也通过大涡模拟的方法得到了并列双方柱压力的时域过程并进行了频谱分析,发现边界条件完全对称的情况下,对称点压力的频谱不相同。杨群等[10]开展的风洞试验发现,并列双方柱的中心距离与方柱边长的比值为2~3时,脉动气动力会发生比较明显的突升现象,需引起设计的重视。并列双方柱的以上研究方法及研究成果不仅为实际工程的设计提供了参考,也为多柱体结构的气动特性研究提供了借鉴。
并列三方柱结构在实际工程中也时有存在。从笔者收集的文献看,与并列双方柱相比,并列三方柱的气动特性研究明显少很多。Sayers[11]通过风洞试验的方法研究了雷诺数为3×104,中心间距为1.1~3.0倍的方柱边长时,并列三方柱的风压系数和升阻力系数等,发现较小的间距变化会导致升阻力系数的较大改变。郑钦敏[12]采用数值模拟的方法研究了雷诺数为150,中心间距为1.1~9.0倍方柱边长时并列三方柱的绕流问题,确定了五种不同的流动结构及间距比范围,详细讨论了每种流态的漩涡结构、脱落频率和流体力等。More等[13]通过热线和粒子图像测速技术研究了并列三方柱在雷诺数为295时,间距对阻力系数和斯托罗哈数的影响,并根据间距将流动状态分为不对称偏压、对称偏压和弱相互作用三种。
综上所述,并列三方柱的气动特性研究较少,且基本在很小的雷诺数或间距范围下开展,研究结果对于桥梁的墩塔、高层建筑群等土木工程结构的设计参考有限。为了更加全面地掌握并列三方柱的气动特性,为实际土木工程中并列三方柱结构的抗风设计提供指导,通过刚性模型测压风洞试验的方法,在较高雷诺数下,测试并分析研究了多个不同间距时并列三方柱的气动特性。
1 风洞试验概况
1.1 试验模型与设备
在石家庄铁道大学的大气边界层风洞实验室的低速段开展试验,该试验段的宽×高×长尺寸为4.38 m×3 m×24 m,最大风速约30 m/s。试验在空风洞均匀流场中进行,背景湍流度小于0.5%。
试验照片如图1所示,并列三方柱模型通过顶部和底部的刚架固定在低速试验段,移动方柱的相对位置即可改变方柱之间的间距。为消除模型的端部效应,保证流场的二元性,在模型两端布置了端板。方柱模型由ABS板制作而成,高度为2 000 mm,横断面边长80 mm。在模型纵向中间位置,沿周向布置测压孔。每个方柱模型每条边15个,共60个测点。考虑到4个直角附近流动参数变化剧烈,测压孔这些位置相对较密。为后文描述方便,将方柱4个角点进行编号,方柱模型的具体测点布置及尺寸,如图2所示。模型前方来流风速和模型表面不同位置测点的风压分别由眼睛蛇风速仪和电子压力扫描阀测得。试验阻塞率约为3.6%,小于5.0%。

图1 试验照片
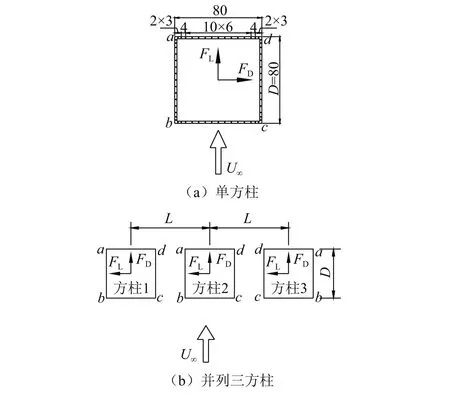
图2 方柱模型的测点布置及尺寸(mm)
1.2 参数定义
不同间距比下方柱的风压分布可用无量纲风压系数表示,定义为
(1)
式中:Pi为模型表面某测点处测得的瞬时压力信号的时间序列;Ps为参考点处的静压值;ρ为空气密度;U∞为模型远前方来流的风速。
平均风压系数Cp,mean和脉动风压系数Cp,rms可定义为
(2)
(3)
式中,N为采样点数,本试验采样点数为9 900。
不同间距比下方柱的气动力可用无量纲阻力系数和升力系数表示,定义为
(4)
(5)
方柱的平均阻力系数和平均升力系数定义为
(6)
(7)
方柱的脉动阻力系数和脉动升力系数定义为
(8)
(9)
式中,FD(i)和FL(i)分别为各测点压力积分得到的方柱单位长度上的顺风向阻力时程和横风向升力时程。
不同间距比下方柱的旋涡脱落特性可用无量纲参数斯托罗哈数表示,定义为
(10)
式中:f为旋涡脱落频率;D为模型特征尺寸。由不同间距比时方柱的升力系数时程进行傅里叶变换得到。
1.3 试验的准确性验证
为验证试验的准确性,先进行单方柱的试验,后进行并列三方柱的试验。本文采用刚性模型测压风洞试验方法进行并列三方柱气动特性研究。为了提高模型的刚度,通过内部设置横隔板和中间布置方钢整体支撑的方式,尽可能提高模型的刚度。虽然采取了以上措施,也不能保证模型足够刚。为此,针对单方柱,先试吹了两种不同的风速,6 m/s和10 m/s。方柱各个面的风压系数如图3所示,两种不同风速下的风压系数差别很小。本文试验得到的平均风压系数与已有文献吻合较好,脉动风压系数与已有文献相比略有差别。脉动风压系数的差异可能与不同的试验条件有关。试验也观测到:当风速为6 m/s时,模型基本静止不动,而当风速为10 m/s时,模型中间部位发生了轻微晃动。为保证三方柱相对来流呈严格的并列布置,三方柱的试验仅在6 m/s的风速下进行,对应的雷诺数约为3.2×104。三方柱模型间距比L/D(L为相邻两方柱的中心距,D为方柱的边长)的取值分别为1.2,1.4,1.6,1.8,2.0,2.5,3.0,3.5,4.0,4.5,5.0,6.0,7.0,8.0。为后文描述方便,将两侧方柱分别命名为方柱1和方柱3,中间方柱命名为方柱2。
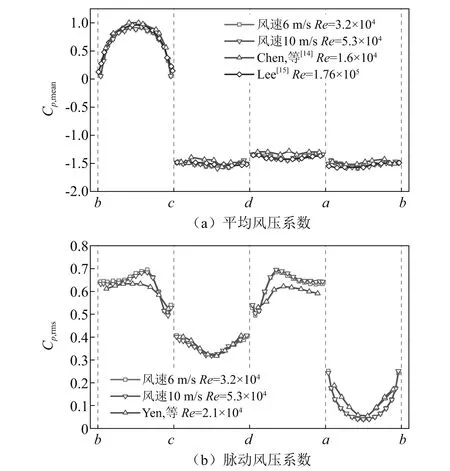
图3 单方柱的风压系数对比
2 试验结果与分析
2.1 平均气动力特性
并列三方柱的平均阻力系数随间距比的变化规律,如图4所示。可以看到:①当1.2≤L/D≤2.0时,两侧方柱(方柱1和方柱3)的平均阻力系数随间距比的增大,均为先减小后增大。两侧方柱平均阻力系数均小于单方柱,且方柱3的减小效应更显著。间距比从2.0增加到2.5时,两侧方柱的平均阻力系数突然增大。当2.5≤L/D≤8.0时,两侧方柱的平均阻力系数大致相等,接近单方柱的值。②中间方柱(方柱2)的平均阻力系数在1.2≤L/D≤3.0时小于单方柱,且随着间距的增大表现出先增大后减小的变化规律;当间距比从3.0增大到3.5时,平均阻力系数突然增大,接近单方柱的值;当3.5≤L/D≤8.0时,中间方柱的平均阻力系数接近单方柱的值。
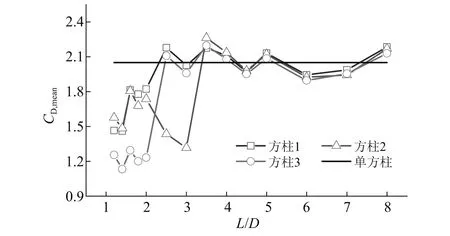
图4 并列三方柱的平均阻力系数
图5将并列三方柱平均阻力系数的均值(3个方柱的平均阻力系数相加再除以3)与More等的结果(试验雷诺数为295,L/D的变化范围为1.5~3.0)进行了对比。可以发现:①雷诺数不同,单方柱的平均阻力系数不同,低雷诺数时单方柱的平均阻力系数更小一些。②雷诺数为295时,3个方柱平均阻力系数的均值随L/D的增大逐渐减小,并接近单方柱的值;雷诺数为3.2×104时,3个方柱平均阻力系数的均值随L/D的增大大致呈逐渐增大的趋势,并逐渐接近单方柱的值。由此表明,雷诺数不同,并列三方柱的气动力特性也不一样。
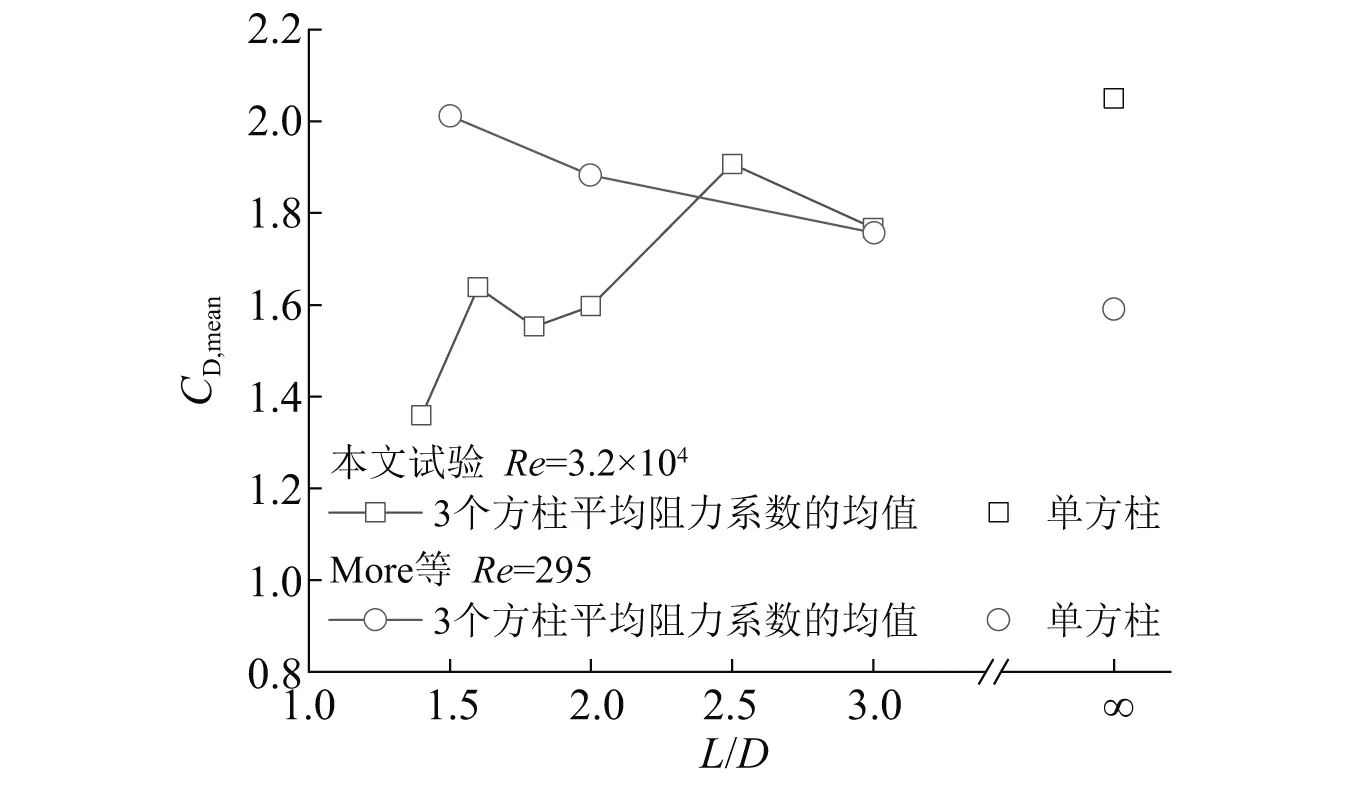
图5 不同雷诺数时并列三方柱平均阻力系数的均值对比
并列三方柱的平均升力系数随间距比的变化曲线,如图6所示。从图6可以比较清楚地看到并列三方柱平均升力系数的变化规律。①当1.2≤L/D≤2.0时,两侧方柱平均升力系数的绝对值均先增大后减小,但绝对值并不相等,且L/D=2.0附近时,平均升力出现方向一致的情况。当间距比从2.0增加到2.5时,两侧方柱平均升力系数的绝对值突然增大。当2.5≤L/D≤8.0时,两侧方柱的平均升力系数大小相等,方向相反。值得注意的是,当2.5≤L/D<3.5时,平均升力系数的绝对值迅速减小,当3.5≤L/D≤8.0时,平均升力系数的绝对值逐渐接近0值。②当1.2≤L/D≤2.0时,中间方柱出现了非0的平均升力系数,最大值约为0.5左右。当间距比从2.0增加到2.5时,平均升力系数接近0值。

图6 并列三方柱的平均升力系数
不同间距比时,并列三方柱的平均风压系数,如图7所示。可以发现,不同间距时三方柱的迎风面的平均风压系数均为正值,表明迎风面均受到风压作用;其余3个面的平均风压系数均为负值,表明其均受到风吸作用。虽然不同间距时三方柱各个面平均风压系数的正负号一致,但具体的数值大小却存在一定的差异。

图7 并列三方柱的平均风压系数
当L/D=1.4和L/D=2.0时,两侧方柱迎风面的驻点向中间方柱偏移,中间方柱迎风面的驻点向方柱3偏移。三方柱背风面平均风压系数的绝对值明显小于单方柱,导致3个方柱的平均阻力系数小于单方柱。两侧方柱各对应面的风压系数并不重合,表明来流经过三方柱后,流场变得不对称,受此影响,中间方柱两侧面的平均风压系数不对称,导致其出现了非0的升力系数。
当L/D=2.5和L/D=3.0时,中间方柱两侧面的平均风压系数基本对称,集中在-0.75左右,大于单方柱的值。两侧方柱外侧面的平均风压系数大致相等,内侧面平均风压系数绝对值由角点c~d先减小后逐渐增大,在角点d附近小于单方柱的值,其余面的平均风压系数接近单方柱的值。以上现象表明此时不存在偏流。
当L/D=3.5和L/D=7.0时,两侧方柱各对应面的平均风压系数基本吻合,且随着间距的增大,逐渐接近单方柱的平均风压系数。中间方柱两侧面的平均风压系数呈对称分布,也随着间距的增大接近单方柱,说明此时不仅不存在偏流现象,且三方柱之间的干扰效应逐渐减弱。
2.2 脉动气动力特性
并列三方柱的脉动阻力系数随间距比的变化规律,如图8所示。①当1.2≤L/D≤2.0时,两侧方柱的脉动阻力系数先减小后逐渐增大,但始终小于单方柱;当间距比从2.0增加到2.5时,两侧方柱的脉动阻力系数突然增大,且明显大于单方柱;当2.5≤L/D≤8.0时,随着间距比的增大,两侧方柱脉动阻力系数逐渐减小接近单方柱。两侧方柱的脉动阻力系数在1.2≤L/D≤3.0时存在一些差异,在其他间距时基本接近。②中间方柱在1.2≤L/D≤3.0时,脉动阻力系数随间距比的增大先减小后缓慢增大;间距比从3.0增大到3.5时,脉动阻力系数突然增大,且明显大于单方柱;当3.5≤L/D≤8.0时,脉动阻力系数接近两侧方柱的值。
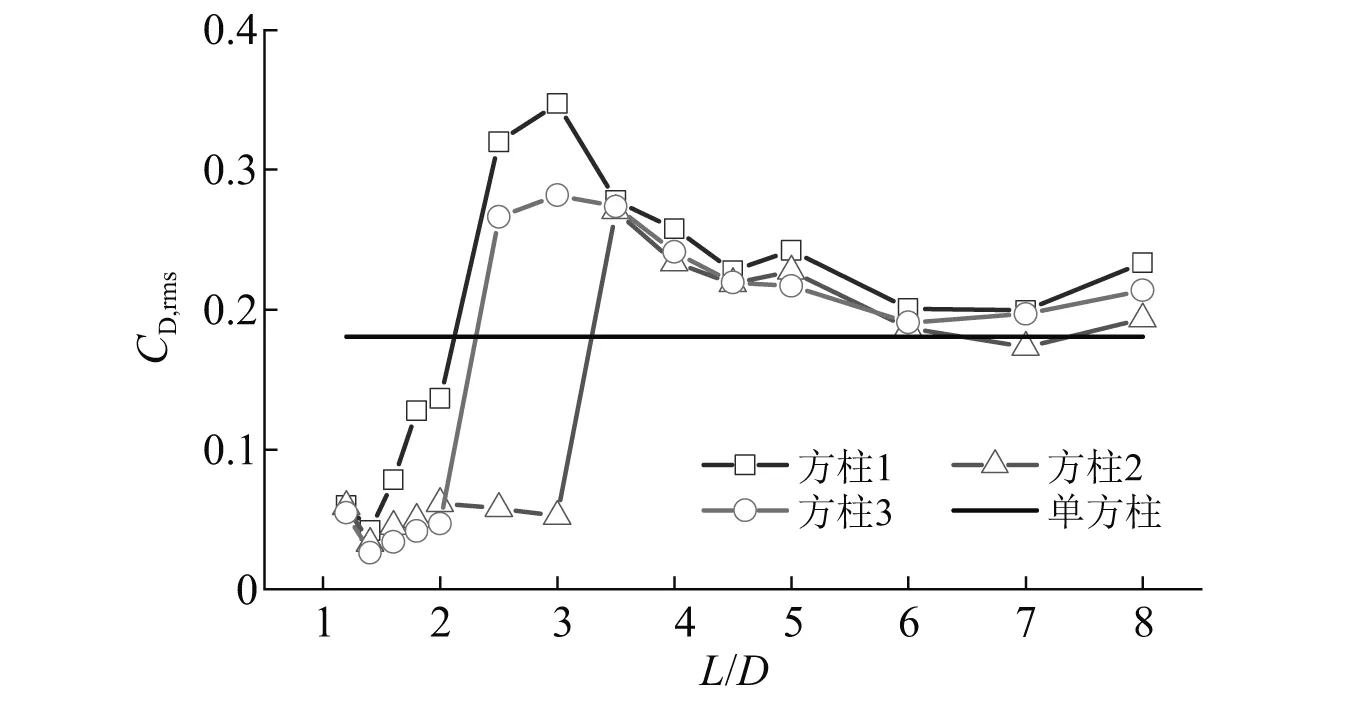
图8 并列三方柱的脉动阻力系数
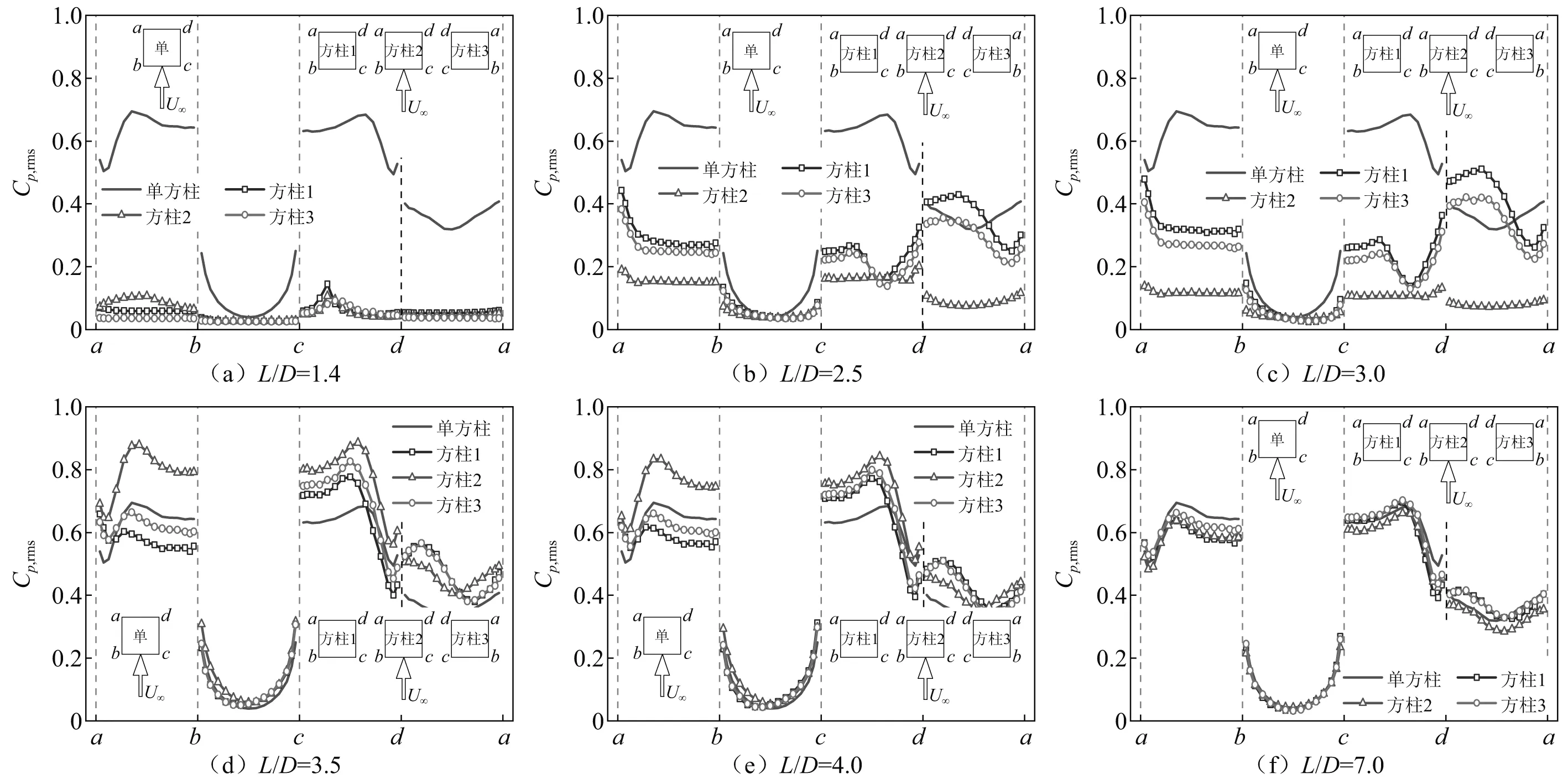
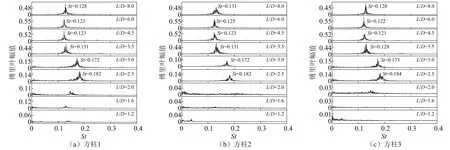
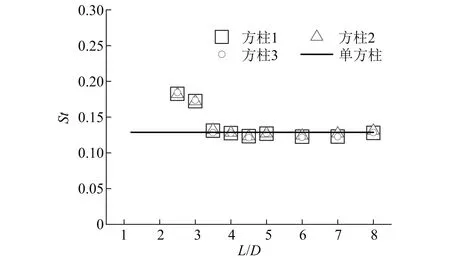
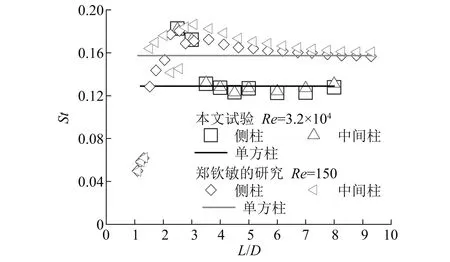
并列三方柱的脉动升力系数随间距比的变化曲线,如图9所示。当1.2≤L/D≤3.0时,三方柱的脉动升力系数随间距比的增加逐渐增大。间距比从3.0增加到3.5时,脉动升力系数突然增大。当3.5≤L/D≤8.0时,三方柱的脉动升力系数逐渐减小接近单方柱的值。值得注意的是,三方柱脉动升力系数发生突变的间距比均为3.0 图9 并列三方柱的脉动升力系数 图10显示了不同间距比时,并列三方柱的脉动风压系数表面分布情况,并与单方柱的结果进行了对比。 当L/D=1.4时,3个方柱各个面的脉动风压系数均非常小,接近0值,说明在小间距时由于相互间的干扰,旋涡脱落受到明显的抑制。 随着间距比的增大,当L/D=2.5和L/D=3.0时,两侧方柱各个面的脉动风压系数均有所增大,但始终小于单方柱的值。两侧方柱内侧面的脉动风压系数由角点c~d,先基本不变后逐渐减小,最后逐渐增大;而外侧面的脉动风压系数由角点a~b,则呈现出逐渐减小的变化规律。中间方柱的脉动风压系数虽然也有所增大,但与两侧方柱相比,增大幅度更小,且沿各个面的分布也更均匀。 当L/D由3.0增大到3.5时,三方柱的脉动风压系数突然增加。两侧方柱外侧面和迎风面的脉动风压系数接近单方柱的值,内侧面和背风面的脉动风压系数大于单方柱的值。中间方柱的两侧面及背风面的脉动风压系数均显著大于单方柱的值。 随着间距比的进一步增加,如图10(e)和图10(f)所示,三方柱脉动风压系数的放大效应逐渐减弱,逐渐接近单方柱的脉动风压系数分布,这说明三方柱间的气动干扰逐渐减弱。 图10 并列三方柱的脉动风压系数 不同间距比时,并列三方柱的升力系数时程幅值谱图,如图11所示。 由图11可见,当1.2≤L/D≤2.0时,3个方柱的幅值谱图均没有出现特别明显的卓越频率,表明三方柱的旋涡脱落受到了明显的抑制。当L/D≥2.5时,三方柱的幅值谱图中均存在峰值频率,说明此时3个方柱存在比较明显的旋涡脱落。从图12可以看到,3个方柱的斯托罗哈数大致相等,随着间距比的增大,斯托罗哈数逐渐减小,接近单方柱的值。值得注意的是,当2.5≤L/D<3.5时,三方柱的斯托罗哈数明显大于单方柱的斯托罗哈数。 图11 不同间距比时升力系数的傅里叶幅值谱 图12 并列三方柱的斯托罗哈数随间距比的变化曲线 图13将并列三方柱的斯托罗哈数与Sayers的数值计算结果(雷诺数为150,L/D的变化范围为1.1~9.0)进行了对比。可以看出:①雷诺数为150时,单方柱的斯托罗哈数约为0.16,大于本文高雷诺数试验结果。②两种不同雷诺数时的斯托罗哈数变化规律既有相似之处,也存在一些差异。当2.5≤L/D≤3.0时,三方柱的斯托罗哈数均大于单方柱的值,之后随着L/D的增大均逐渐接近单方柱的值。在小间距时,本文试验发现三方柱的旋涡脱落现象不明显;而雷诺数为150时,三方柱存在斯托罗哈数,表明与高雷诺数不同,较低雷诺数下三方柱在小间距时也存在较明显的旋涡脱落现象。以上分析表明,雷诺数不仅对并列三方柱的气动力特性产生影响,也影响其旋涡脱落特性。 图13 不同雷诺数时斯托罗哈数对比 利用刚性模型测压风洞试验的方法,测试并分析了不同间距时并列三方柱的平均气动力特性、脉动气动力特性及旋涡脱落特性,主要得到了以下结论: (1)当1.2≤L/D≤2.0时,并列三方柱的绕流存在明显的偏流现象。两侧方柱的气动力不等,中间方柱会受到非0的平均升力作用。当L/D≥2.5时,偏流现象基本消失。当L/D≥3.5时,三方柱的气动干扰效应随着间距的增大逐渐减弱,三方柱的气动特性逐渐接近单方柱。 (2)当L/D由2.0增加到2.5时,两侧方柱的脉动阻力系数会突然增大。当L/D由3.0增加到3.5时,中间柱的脉动阻力系数和三方柱的脉动升力系数会突然增大。这2个临界间距时脉动气动力的突升现象需引起结构设计的重视。 (3)当1.2≤L/D≤2.0时,并列三方柱的旋涡脱落受到了明显的抑制。当L/D≥2.5时,并列三方柱均存在比较明显的旋涡脱落,且对应的斯托罗哈数大致相等。三方柱的斯托罗哈数在2.5≤L/D<3.5时明显大于单方柱的斯托罗哈数,在L/D≥3.5时接近单方柱的斯托罗哈数。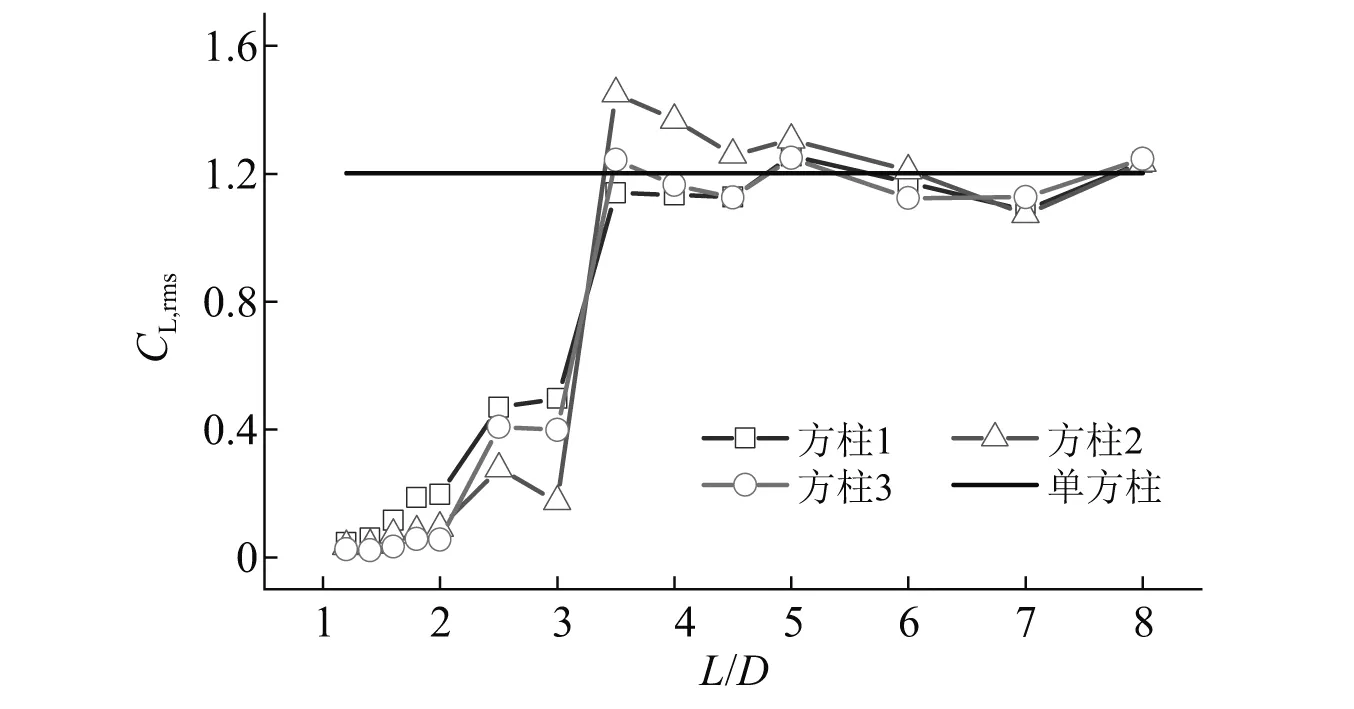
2.3 旋涡脱落特性
3 结 论

