一种滚动密封爬壁机器人的安全吸附条件与运动特性分析

姜德政 胡 军 钟 恒 王洪光 宋屹峰 袁兵兵,4

1.中国长江三峡集团有限公司，北京，100038 2.中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳，110016 3.中国科学院机器人与智能制造创新研究院，沈阳，110016 4.中国科学院大学，北京，100049

0 引言

大坝、流道等大型混凝土建筑表面长期处于野外暴露状态，存在裂缝、表面剥落、冲击坑等缺陷，需要定期进行检测和维护。三峡工程中大坝的排漂孔流道中约有6 km行程需要定期开展检测，流道内的高差大、壁面复杂，传统人工方式检测劳动强度大、覆盖能力弱，还存在一定的作业危险性。

爬壁机器人技术已经相对成熟，检测效率与安全性较高，在壁面检测领域越来越受到人们的重视[1]。目前利用机器人开展混凝土壁面检测时多采用负压吸附，按照吸附腔与壁面相对运动关系可划分为固定吸盘式[1-3]、滑动吸盘式[4]、滚动密封式[5-6]等。其中，滚动密封式履带爬壁机器人具有密封结构耐磨、负载能力大、运行速度快[5-6]等特点，符合混凝土建筑表面的检测需求。由于机器人吸附于垂直壁面，吸附力不足造成的脱落或大范围滑移运动失准都将导致任务失败，故保持稳定吸附与准确运动成为执行检测任务的必要条件，也成为爬壁机器人研究的重点方向之一。

目前通常利用转向动力学模型对吸附稳定性与运动准确性开展研究，滑动吸盘式[2,4,7-9]和履带式[10-12]两种结构密封机理与摩擦力受力情况不同，用于分析的模型也存在一定差异。因为结构类似，地面履带车转向模型[11-15]常被当作履带式爬壁机器人的基础分析模型，在改变受力方向、参数简化的基础上进行进一步分析。但在开展模型分析时，应着重考虑履带式爬壁机器人的结构特殊性，具体包括：①履带宽度，为保证密封效果，驱动履带宽度占机器人宽度1/3，因此，不可忽略履带宽度；②因驱动履带、密封履带与墙壁接触面间的负压而产生的摩擦力；③转向中的滑移量，提高负压可以抑制转向过程中的滑移[13]，若不抑制转向中的滑移量，机器人可能因滑移量过大后遇到未知的壁面缺陷而掉落。

针对以上问题，为了提高滚动密封式移动机器人的吸附稳定性与运动准确性，本文着重分析了履带宽度、履带对壁面不均匀正压力、负压吸附等参数对滑移过程的影响，揭示滚动密封爬壁机器人的安全吸附条件，建立滚动密封履带式机器人滑移转向动力学方程，对机器人运动准确性进行分析，最后通过MATLAB仿真及实验进行充分验证。

1 滚动密封履带式爬壁机器人模型

1.1 爬壁机器人机构设计

爬壁机器人结构如图1所示，它分为底盘和控制箱体两个部分。控制箱体上安装有前后两个视觉传感器，以提供缺陷检测和导航的功能；控制箱体上安装有用于传输图像及控制信息的图传、数传设备；控制箱体内部装有电池。机器人底盘为滚动密封的履带式移动载体，如图1a 所示，左右驱动履带分别由电机控制，以实现机器人的平动和转向；图1b 中，密封履带3～6中每一条都由柔性海绵支撑滚子所支撑，保持被动密封履带3～6与壁面的柔性接触。左右驱动履带1、2，前后密封履带3～6，密封腔盖板7，共同围成了一个碗状空腔。该空腔和壁面贴合后形成一个密封腔。负压风机从密封腔内抽气形成负压。滚动密封机理与滑动密封机理相比，优点在于构成密封腔的密封履带3～6会随着驱动履带1、2转动，滚动时密封履带的磨损会大大小于平动密封方式静摩擦造成的磨损。

(a)爬壁机器人结构

1.2 运动机理分析

机器人的履带式移动底盘吸附墙面后，负压腔产生负压力，该负压力将机器人压紧在壁面上，使得机器人不打滑、不倾覆。如图1b 所示，驱动履带1、2以相同速度运动则驱动机器人平动，驱动履带1、2差速运动时则机器人进入转向状态。特别地，若驱动履带1、2速度值相同、方向相反，则机器人达到理论半径为0的原地转向状态。分别对平动及转动时机器人的运动机理进行分析。

当机器人以任意姿态(水平、竖直、斜向)平动时，机器人保持可靠运动的前提条件是履带上摩擦力能够克服重力，即机器人不打滑，同时机器人的负压力应能够克服重力产生的倾覆力矩，即机器人不倾覆。由上分析可知，增大机器人的负压力则机器人对壁面的正压力增大，进而提供的摩擦力增大，能够使机器人在平动情况下不打滑和不倾覆。

机器人转向过程有两个方面需要注意：较小负压力会造成较大的滑移，将降低机器人转向过程安全性；较大的负压力将引起较大的横向摩擦阻力，直接增加驱动电机的负载，降低工作效率。此外，机器人转向过程中会发生滑移现象[11-15]，由于重力平行于移动平面且竖直向下，故滑移现象较地面上严重，转向过程中质心滑移量较大。由图1a可知，机器人只有前后视觉而无侧向视觉，若机器人质心滑移量较大，机器人会产生较大的侧向位移分量，该方向的位移处于机器人视觉盲区。混凝土大坝上壁面情况复杂，凸起、水泥凸棱较多，若滑移量较大，机器人遇到未知壁面缺陷的可能性会增大，从而降低转向过程的安全性。

综上可知，增大机器人负压力可以有效削弱滑移现象，减小质心滑移量。但在转向工况下，机器人因有横向速度分量，会受到横向摩擦阻力，该摩擦阻力随负压力增大而增大，因而单纯通过增加负压力削弱滑移会增加驱动电机负载，降低驱动效率。因此，有必要建立转向过程动力学模型以求解机器人负压力、转向半径、速度、负载等与质心滑移量的关系。在给定负载下，定量地给出质心滑移量与负压力的关系，据此可合理选择负压力，以获得较高的转向安全性和较小的驱动力，以上安全吸附条件分析框图见图2。

图2 爬壁机器人安全吸附条件分析Fig.2 Analysis of instability conditions of wall climbing robot

2 滚动密封爬壁机器人安全吸附分析

2.1 爬壁机器人平动工况下安全吸附条件

为分析机器人在静止或者直线行走状态下抗打滑及抗倾覆的稳定吸附条件，在传统履带车辆动力学[15]基础上增加以下假设：①爬壁机器人在竖直面内低速匀速转向，忽略不计离心力；②图1中密封履带3～6为柔软海绵支撑，忽略其对机器人提供的支撑力。

当爬壁机器人运行于竖直壁面按一定半径转弯时必须克服重力的作用。在不同姿态角下，重力产生的横向倾覆力矩和纵向倾覆力矩不同。履带上的载荷分布随着爬壁机器人姿态角的不同而发生较大变化，载荷在履带上的分布状态与爬壁机器人姿态角和重力直接相关。

任意姿态爬壁机器人静止或者匀速运动在竖直壁面上的情形如图3所示，首先定义竖直墙壁上随着爬壁机器人运动的平动坐标系OXYZ，XOY平面为平行于墙壁的竖直平面，Z轴垂直墙壁表面，X方向为水平方向，Y方向为竖直方向，O为爬壁机器人底盘的几何中心。Oxyz为固定在爬壁机器人上的坐标系。xOy平面与竖直平面重合，z轴方向垂直墙壁表面，x轴方向为爬壁机器人横向，y轴方向为爬壁机器人纵向，原点O固定在爬壁机器人底盘几何中心。Oy方向为爬壁机器人直行运动方向,θ为爬壁机器人的姿态角。

图3 爬壁机器人受力分析Fig.3 Force analysis of wall-climbing robots

机器人静止或匀速直线运动的力平衡下，负压应满足的条件为

(1)

其中，y为履带上点的纵坐标；k为比例系数；fni0为履带中点摩擦力；其余各参数物理意义见表1。为了保证安全吸附，需要保证:fni>0(i=1,2)，履带i上的摩擦力Ffi满足线性分布fni。

表1 基本物理参数Tab.1 The basic physical parameters

另外，爬壁机器人由于重力产生倾覆力矩，爬壁机器人转弯时安全吸附条件可以假设为爬壁机器人满足以下约束方程：

(2)

综合式(1)与式(2)，得到滚动密封爬壁机器人平动时的安全吸附条件：

(3)

式中，μ为驱动履带和壁面之间的摩擦因数。

2.2 滑移转向过程动力学平衡方程

设计机器人时需要对恶劣工况下的驱动力进行准确计算。对于滚动密封爬壁机器人，在转向工况下，履带上摩擦阻力矩最大，故可通过建立转向过程的动力学模型来进行机器人驱动力的计算与驱动电机选型。以WONG等[13]研究的地面履带车转向机理为基础，忽略密封履带的支撑力但考虑由密封履带与壁面接触面的负压力引起的摩擦力，结合爬壁机器人特殊的载荷情况，建立爬壁机器人的模型，参数设置见表1。

因为滑移现象通常会出现在履带式爬壁机器人转弯过程中，所以履带仅在Osi处的速度vOi与履带卷绕速度vqi相同[14]，i=1,2，即

(4)

(5)

(6)

引入滑转率δi的评价指标，其计算公式如下：

(7)

驱动履带结构上由同步带及其外层粘接的泡棉层组成，在转弯过程中履带与接触面间的摩擦阻力可以分为两部分：驱动履带上的摩擦阻力和被动密封履带的摩擦阻力。以驱动履带速度瞬心Osi为建立驱动履带的局部坐标系原点，x轴选定为驱动履带的横向方向，y轴选定为驱动履带的纵向方向，如图4所示。为完成爬壁机器人的摩擦阻力分析，对模型做以下简化假设：①驱动履带上载荷成梯形分布；②密封履带与驱动履带与壁面之间存在均匀分布的负压；③爬壁机器人在竖直硬地面做低速匀速转弯，履带上与壁面接触每点的摩擦剪力方向与该点在转向瞬间的速度方向相反。

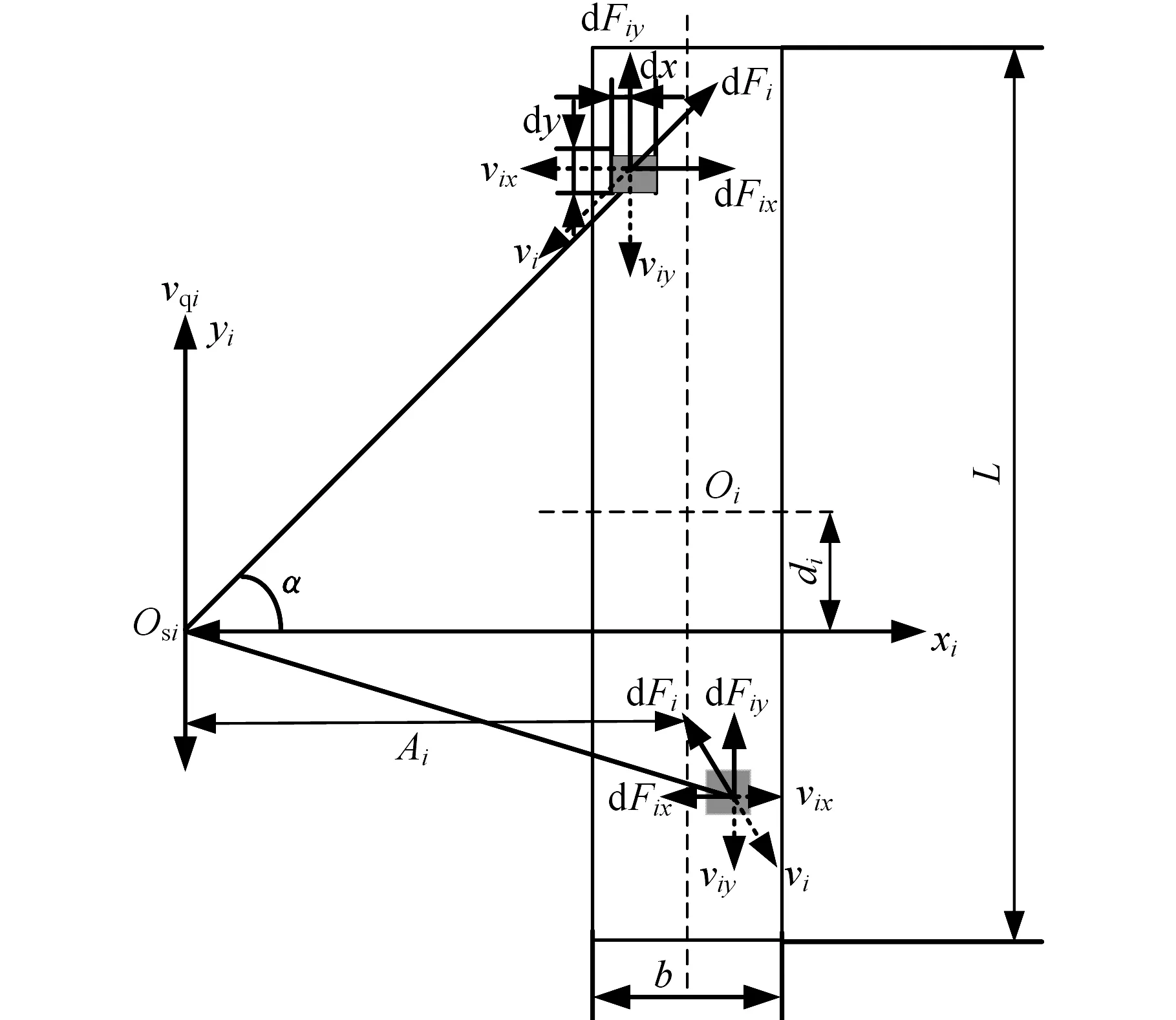
图4 驱动履带受到的摩擦阻力Fig.4 Friction resistance to tracks

爬壁机器人转弯时产生的重力分量使爬壁机器人质心发生偏移，偏下侧驱动履带的载荷增大，偏上侧驱动履带的载荷较小，基于密封履带上负压的均匀分布且密封履带柔性支撑的假设，可知密封履带上所受摩擦力均匀分布，四条密封履带上的摩擦阻力分布如图5所示。在驱动履带接地面选取一个微元，则爬壁机器人在该处产生的摩擦阻力如图4所示。

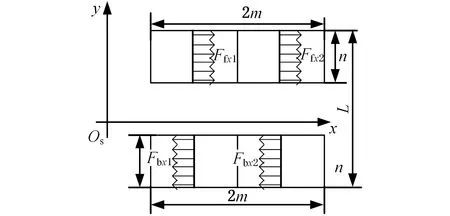
图5 密封履带受到的地面摩擦阻力Fig.5 Ground friction resistance to passive tracks

在履带接地段上任意微元处，摩擦力的方向与速度矢量之和的方向相反。在x轴与y轴上的分量为

(8)

(9)

其中，fqi(i=1,2)为驱动履带接地段在微元处的压力，包含两个部分：机器人对壁面的压力与负压腔泄漏的负压造成的履带对壁面的压力，微元的宽度为dxi、高度为dyi。α为该微元与履带的速度瞬心之间的夹角。故可得到第i条履带上微元在xi、yi方向上的摩擦力dFix、dFiy，Vix、Viy分别为第i条履带中轴线处速度在x、y方向的分量，di为履带速度瞬心Osi相对于履带形心Oi在y方向上的偏置，两条履带偏置量相等，即d=di(i=1,2)。对式(8)积分，得到地面对行走履带产生的摩擦力在x、y方向上的分量：

(10)

所有的横向摩擦力Fix及其力矩Mfi均为阻力，而所有纵向摩擦力的合力均为驱动力，所有矩心均取爬壁机器人形心。摩擦阻力矩Mf和驱动力矩MT表达式为

(11)

密封腔的泄漏负压形成均匀分布的正压力存在于密封履带与壁面间，等效为沿履带纵向轴线均匀线性分布，同时密封履带上纵向摩擦力会带动密封履带滚动，因此，该部分摩擦力可忽略不计，只考虑密封履带上的横向摩擦力。此时，四条履带上横向摩擦力分别为Ffx1、Ffx2、Fbx1、Fbx1，可表示为

(12)

其中，密封履带上横向和纵向上的摩擦力合力为零，对机器人形心取力矩为密封履带所受摩擦阻力距Mfb，负号表示阻力矩方向为顺时针。

同时考虑到爬壁机器人的力学平衡，获得以下平衡方程：

(13)

负载在xoy平面内的转向阻力矩MN为

MN=-NSsinθ

(14)

综上，得到爬壁机器人匀速转弯时的转向力矩平衡方程：

MT+Mf+MN+Mfb=0

(15)

则式(15)与式(13)共同组成转向时的安全吸附条件。

2.3 滑移转向过程安全吸附条件

爬壁机器人控制左右履带差速实现转向时，存在爬壁机器人质心滑移的实验现象。如图1b所示，机器人无侧向(机器人本体坐标系的x方向)视觉，机器人在滑移过程中，质心滑移过大将使机器人在侧向产生较大位移，进而机器人可能滑移到未知缺陷区域而掉落。为了保证机器人吸附安全性，需将滑移引入安全吸附条件中。

消减滑移需要增大负压力，考虑电机功率和输出扭矩的限制，将转向下的滑移消减到足够小即可。机器人质心下滑距离为kyB，水平滑动距离为kxB，其中，ky、kx分别为纵向、横向滑移系数。因此，得到限制爬壁机器人质心滑移量需要满足以下吸附条件公式：

(16)

考虑机器人理论转向半径为0时的滑移，有vq1=-vq2，则式(16)化简为

(17)

满足式(16)的最小负压力Fp记为Fp2。则可得到安全吸附条件公式：

(18)

式中，μ1为壁面摩擦因数；Fp1为不倾覆所需最小负压。

3 仿真与实验分析

3.1 爬壁机器人滑移下安全吸附条件仿真

为定量给出质心滑移系数与负压力的关系，需要先对影响滑移系数的因素：负载、转向半径、负压力与滑移系数的关系进行仿真，依据仿真结果选择滑移最恶劣的工况下建立滑移系数与负压力的关系。

(1)滑移系数与转向半径。在外侧履带卷绕速度vq2=0.1 m/s、负载10 kg、负压力800 N情况下，仿真得到机器人的滑移系数与转向半径的关系，如图6a所示。外侧履带卷绕速度固定不变的情况下，转向半径越大，转向90°后机器人的质心滑移系数越小。当转弯半径为0时，滑移系数最大，竖直滑移系数是0.25，水平滑移系数是0.13。因此，以原地转向90°时的滑移系数ky衡量机器人转向后的质心滑移水平。

(2)理论转向半径为0时，最小负压条件条件下滑移系数与负载关系。如图6b所示，最小负压条件(式(3))下，爬壁机器人不同负载情况下最小负压随负载线性变化且与角速度无关。如图6c所示，在恒满足式(3)时，滑移系数ky随负载变化不明显，且角速度变化引起的滑移系数变化不大。负载10 kg时所需最小负压力为245.5 N，此时滑移系数ky为1，即机器人原地转向90°将下滑1倍机器人宽度，下滑量过大。如图6a所示，同样负载条件和角速度下，负压800 N，此时机器人下滑系数ky为0.25，下滑量变为原来的1/4，机器人转向的安全性提高。由此可知，考虑机器人滑移限制的负压稳定性条件式(18)是有必要的。

(3)理论转向半径为0时，带负载工况下滑移系数与吸附力关系。理论转向半径为0，不同负载下机器人的负压力与滑移系数ky的关系如图6d所示。可以看出随着负压增大，机器人的滑移现象被抑制；滑移系数主要受负载和负压力影响。

(a)ky-R关系(b)式(3)条件下Fp-N关系

(4)限制滑移的安全吸附条件下驱动力仿真。由图6d可得到滑移系数与负压力的直接关系，为保证运动准确性，应保证滑移系数不大于0.25，在设计额定负载为10 kg时，应至少保证800 N的负压吸附。同时，由滑移曲线变化也可看出，传统的履带转向动力学模型忽略了履带宽度和转向滑移，对爬壁机器人并不适用。

基于以上分析，开展机器人滑移转向模型的驱动力仿真与简化模型驱动力仿真对比分析，如图7所示。仿真结果显示，当额定负载10 kg、负压吸附800 N时，本文模型求解得到最大驱动力为397.05 N，履带驱动轮直径为110 mm，转换得到驱动履带最大所需驱动力矩为22.23 N·m。相同吸附力下按照简化模型求解，得到外侧履带最大驱动力为244.14 N，转换得到驱动履带最大所需驱动力矩仅为13.43 N·m，难以为实际设计提供支撑。

图7 外侧履带驱动力仿真对比Fig.7 Changes in the driving force of the outer track

3.2 滚动密封爬壁机器人样机实验

使用本文模型设计得到滚动密封履带式爬壁机器人样机，并在三峡大坝混凝土流道内进行样机实验，如图8所示。在混凝土大坝上机器人携带额定负载转向，测得履带驱动电机最大输出扭矩为22.74 N·m,与仿真结果22.23 N·m接近。

(a)壁面爬行实验、通过性实验、曲面适应性实验

携带15 kg负载下机器人4 kPa(360 N负压力)负压下能够不打滑、不倾覆，但转向过程中向下滑移严重(滑移量系数测量约3.7)；而使用9 kPa负压(产生810 N负压力)时，向下滑移量较小(滑移系数测量约为0.7)。

3.3 实验结果分析

对于滚动密封履带爬壁机器人，转弯半径越小，滑移越明显；转向角速度对滑移的影响相对较小；取理论转向半径为0时的滑移系数为评价机器人转向安全性的指标，该指标主要受负载和负压力大小的影响。本文建立的滚动密封爬壁机器人转向力学模型与实际情况较为符合；实际按照滑移系数限制条件给出的负压力，可以有效抑制机器人滑移，提高机器人转向过程中的安全性，同时对吸附电机与驱动电机选型提供依据，有利于发挥滚动密封履带式爬壁机器人密封结构耐磨性好、负载能力较强、曲面适应性强的优势。

4 结论

(1)本文基于动力学方法，提出了滚动密封爬壁机器人在运动状态下，特别是滑移转向状态下的稳定吸附条件。该条件下建立了关键设计参数与机器人吸附稳定性及运动准确性的联系，为指导机器人优化设计提供理论依据。

(2)对滚动密封爬壁机器人运动机理开展分析，揭示了履带宽度、机器人对壁面不均匀分布正压力、履带和壁面间负压和转向滑移的影响。

(3)分别采用仿真与实验手段，研究负载、转向半径、负压力等关键因素对机器人滑移与稳定吸附的影响。结果表明，建立的滚动密封爬壁机器人转向力学模型与实际情况较为符合，通过合理调整负压、转向半径等参数，可以有效抑制机器人滑移，提高机器人吸附稳定性与安全性。

(4)本文提出的基于滑移转向的动力学模型有利于指导机器人设计，以驱动电机选型计算为例，仿真计算值22.23 N·m非常接近于实测值22.74 N·m，优于传统简化模型的仿真值(13.43 N·m)。

综上，本文提出的安全吸附条件可提高机器人转向过程安全性与运动准确性；转向动力学模型求解驱动力精度较高，可用于指导机器人性能优化设计，且该模型求解的滑移量可为爬壁机器人壁面轨迹规划中补偿、纠正轨迹偏移提供参考。