叶尖定时信号趋势项自适应拟合
刘志博 段发阶 叶德超 冯军楠 熊 兵
1.天津大学精密测试技术及仪器国家重点实验室,天津,300072 2.中国航发上海商用航空发动机制造有限公司,上海,200241 3.中国航发四川燃气涡轮研究院,成都,610500
0 引言
叶尖定时测量方法主要监测叶片周向弯曲振动,通过监测叶片到达传感器时间,进一步计算得到叶片振动位移。由于该类传感器主要用来监测叶片到达时间,故通常被称为定时传感器。该方法自20世纪60年代提出发展至今,目前已涵盖光纤式[1-5]、电容式[6-7]、微波式[8]、电涡流式[9-10]定时传感测量方法。由于定时信号具有欠采样特点,当前大部分研究工作集中在定时信号重构方法上。定时信号重构基于叶片同步振动和异步振动特点,采用曲线拟合或频谱分析方法对叶片振动参数进行辨识。曲线拟合方法主要解决极度欠采样条件下同步振动参数辨识难题,主要有单参数法[11]、双参数法[12]、周向傅里叶拟合方法[13]、自回归法[14-15]、任意角参数辨识方法[16]等。频谱分析方法主要解决欠采样条件下叶片异步振动信号多模态盲重构问题,主要有快速傅里叶变换(fast Fourier transform, FFT)方法[17-18]、“5+2”方法[19]、谱分析(最小方差谱估计[20]、交叉谱估计[21]、子空间谱估计[22])以及定时信号稀疏重构[23]等。为实现叶片振动精准分析,非等间隔采样模型参数辨识和高精度预处理技术已经成为当前迫切需要解决的技术难题。非等间隔采样模型由于考虑了叶片振动对到达时间的影响,更符合实际定时信号采样情况,目前,该方面研究工作主要有改进的单参数辨识方法[24]和改进的周向傅里叶拟合方法[25]等。有键相和无键相到达时间提取、异常值剔除、平滑滤波等都属于定时信号预处理[26],特别是近年来为解决航空发动机转速同步传感器安装难题,提出的无键相条件下叶片到达时间提取方法[27-31]极大地提高了定时测量技术的工程适用性,但目前针对定时信号预处理中其他方面的研究报道较少。
趋势项拟合作为定时信号预处理中的一项重要研究内容,其目的是消除叶片由于受到气流压力而产生的静态偏转位移[32-33]。趋势项不仅对叶片振动事件准确定位造成干扰[34-35],同时会严重影响叶片振动参数准确辨识。当前趋势项拟合主要采用固定窗宽度对定时信号进行多项式拟合[32-33]。在航空发动机连续变工况试验过程中,由于旋转叶片运行流场环境复杂,导致固定窗宽度趋势项拟合难以适应叶片静态偏转变化过程,而通过人工截取特定数据段进行趋势项拟合,一方面费时费力,另一方面难以保证良好的趋势项去除效果,一旦发生过拟合,将破坏原始振动波形,丢失大部分振动信息。
针对变工况条件下定时信号趋势项拟合的难题,本文提出窗宽度可自适应调节的趋势项拟合方法。转子加速度不同导致叶片受到的气流压力不同,进一步导致叶片趋势项不同,故本文以转子加速度变化量为参考,通过判断加速度相对变化量是否大于设定的加速度变化阈值,将加速度变化小于阈值内对应的数据长度作为趋势项拟合窗宽度,采用多项式对窗内的数据进行趋势项拟合,并通过计算去除趋势项前后两列叶片振动数据皮尔逊相关系数,对趋势项去除效果进行评价,若相关系数较小,表明趋势项拟合对原始定时信号波形破坏较大,算法将重新调整预先设置的加速度阈值,并再次进行加速度相对变化与修正的加速度阈值进行比较,重新确定拟合数据窗宽度,并进行趋势项拟合,重复这一过程,直至相关系数大于某一设定阈值为止(本文设定相关系数阈值为0.8)。采用航空发动机高压压气机转速升转过程中的叶尖定时数据对本文方法进行验证。
1 叶尖定时测量方法
叶尖定时测量原理如图1所示,定时传感器安装在机匣上,用于监测叶片到达时间,转速同步传感器安装在转轴附近,通过监测键相标记到达时刻为定时采集系统提供定时基准。当转轴发生弯扭振动时,会破坏键相信号周期性,并进一步影响叶片振动测量的准确性。LIU等[36]提出在叶根处加装一支传感器,通过获得叶根到达时间消除转轴弯扭振动影响,但在实际航空发动机测量时,在叶根处加装传感器是极其困难的,因此,本文按照常规的定时信号处理方法获得叶片振动位移[27],忽略转轴弯扭振动对定时信号的影响,这也是目前工程上通常采取的简化处理方法,且已被验证是满足工程测量要求的[30]。假设监测级叶片数目为B,传感器监测的第b(b= 1, 2, …,B)个叶片到达时间为tb,则叶片b旋转角度
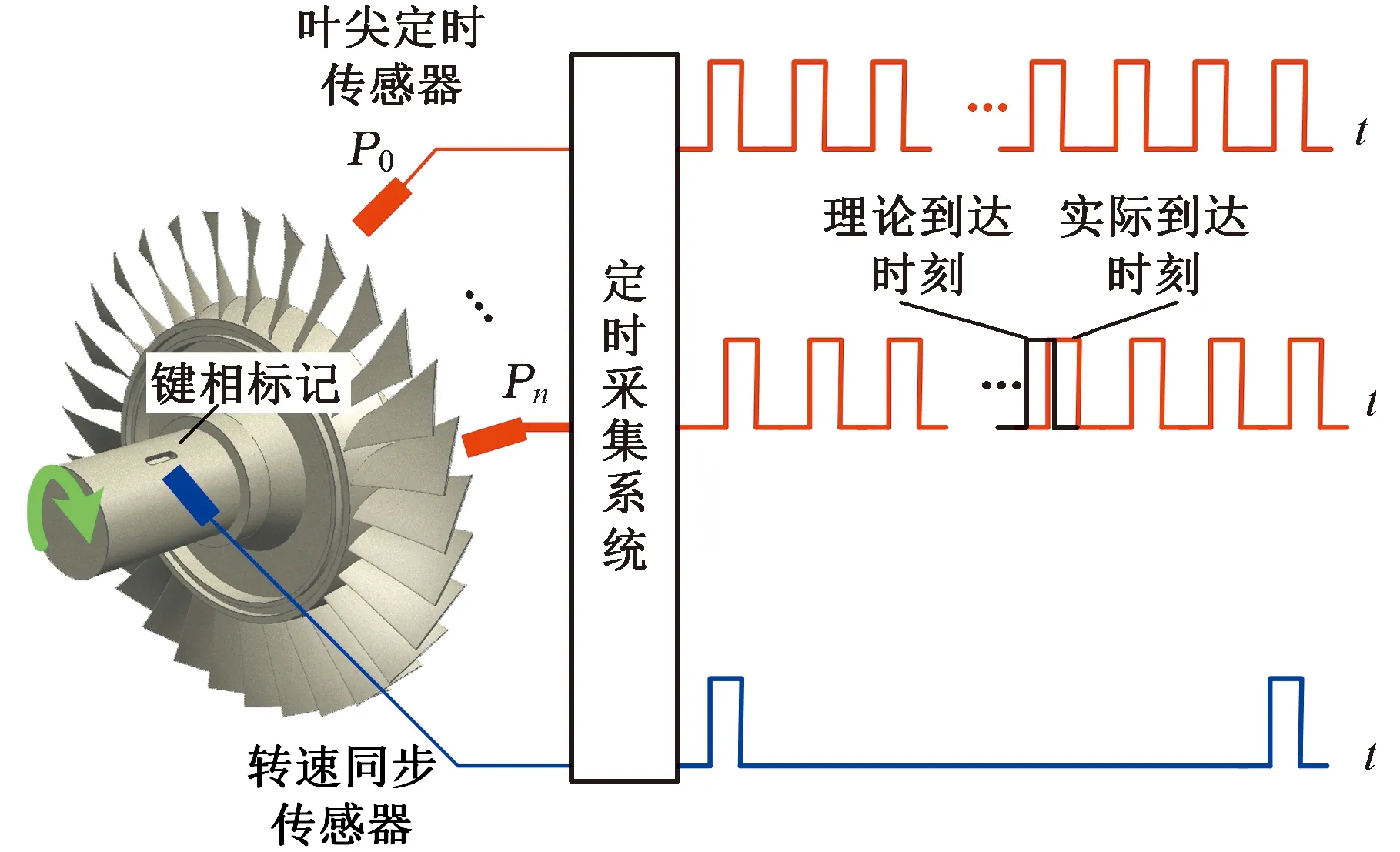
图1 叶尖定时测量原理Fig.1 The scheme of blade tip timing measurement
θb=ωRtb
(1)
式中,R为叶尖到转子中心距离;ω为转子旋转角速度。
令叶片振动位移为y,静态偏转位移为C,如图2所示,灰色部分表示叶片未旋转情况下的几何关系,红色粗实线表示叶片b弯曲振动情形,蓝色粗实线表示叶片b仅发生静态偏转的情形,灰色虚线表示叶片b无振动并且无偏转情形。
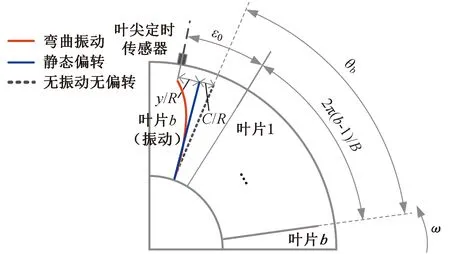
图2 叶片振动测量示意图Fig.2 The scheme of blade vibration measurement
根据叶片旋转角度与叶片振动之间的几何关系[25,30],有
(2)
其中,ε0表示1号叶片在静止状态下距离传感器的初始角度。在低转速情况下,ε0可以通过叶片到达传感器时间计算得到:
ε0=ωdRt1
(3)
式中,ωd为低转速度;t1为低转速下1号叶片到达传感器的时间。
联立式(1)~式(3),得到包含趋势项的叶片振动位移yc:
(4)
为得到叶片振动位移y,需进一步去除叶片趋势项C。本文提出自适应窗宽度的趋势项拟合方法,采用相关系数对趋势项C去除效果进行评价,对于趋势项拟合效果较差的数据段,自适应地调整窗宽度,并重新进行趋势项拟合,直至趋势项拟合效果达到最优。
2 趋势项自适应拟合窗宽度的确定
叶尖定时信号趋势项与航空发动机运行工况紧密相关,由于不同加速度情况下叶片受到气流压力不同,导致趋势项不同,故可将叶尖定时信号趋势项变化简化为转子加速度函数,即
C=f(a)
(5)
其中,a表示转子加速度;f(·)表示函数。可根据加速度变化区间确定需要拟合的趋势项窗宽度。
某型航空发动机试验转速曲线如图3所示,其中,加速度变化如蓝色曲线所示。对应运行区间M1和M3数据段,其转子加速度基本保持恒定,因此,对于该两个区间内采集的叶片振动数据,根据式(5),其趋势项C基本保持恒定,当进行趋势项拟合时,可将M1和M3区间对应的数据长度直接作为拟合窗宽度。
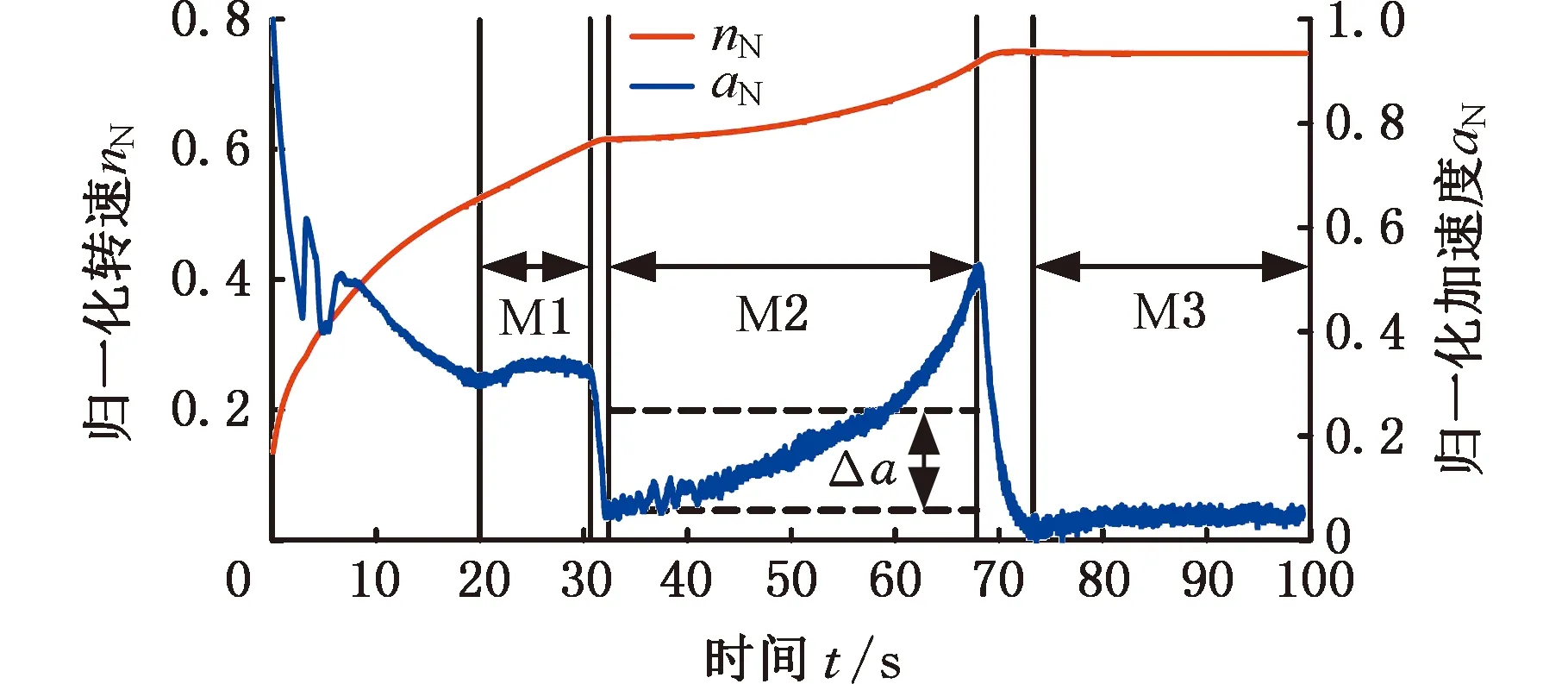
图3 航空发动机叶片振动测量试验转速和加速度曲线Fig.3 Rotating speed and acceleration curve of aero-engine blade vibration measurement test
对于M2试验区间,加速度是一个缓变过程,假设M2区间的起始圈为n,对应的加速度为an,在第n+r圈,对应的加速度为an+r,则加速度相对增量Δa可表示为
Δa=|an+r-an|
(6)
设置加速度变化阈值为a*,当满足下式
Δa>a*
(7)
时,可确定对应的第n~n+r圈为一个趋势项拟合窗宽度。通过设置加速度变化阈值,可初步确定趋势项拟合窗宽度,后续可根据去除趋势项前后两列数据是否满足极度相关关系(皮尔逊相关系数大于 0.8)来对加速度变化阈值进行修正,从而实现拟合窗宽度自适应调整,完成不同周期内的趋势项去除。
3 趋势项拟合系数求解
采用多项式对定时数据趋势项进行拟合,多项式拟合函数基本表达式为
yc=p0+p1x+p2x2+…pmxm
(8)
其中,pi(i=0,1,…,m)为多项式系数,x为拟合自变量,m为多项式拟合阶数。通常叶片趋势项表示一个缓慢变化过程,因此,对趋势项拟合时,通常取m为1。
对第n~n+r圈内的数据序列{yc}进行多项式拟合:

(9)
即
Yc=XP
(10)
基于最小二乘原理[37],得到趋势项为
(11)
则叶片振动位移为
(12)
4 趋势项拟合效果评价
叶尖定时信号趋势项拟合的主要目的是在不破坏叶片原始振动波形的前提下,通过消除拟合趋势项,将叶片振动波形平移至零值水平线附近,因此,拟合残差并不能作为趋势项拟合效果评价指标。本文计算去除趋势项前后两列数据波形的皮尔逊相关系数,相关系数越接近1,则表明两者波形越吻合[38],即趋势项去除对定时信号波形的破坏程度越小,保留的原始振动信息越完备,越有利于后续叶片振动分析。趋势项去除前后两列定时信号皮尔逊相关系数ρ为
(13)
其中,yi和yi*分别表示趋势项去除前后的第i个定时数据,¯y和¯y*分别表示均值。通常皮尔逊相关系数大于0.8时,表示两列数据为极度相关[38]。因此,本文后续评价趋势项去除效果时,以0.8为阈值,当ρ<0.8时,认为趋势项拟合对原始振动波形破坏较大,丢失的振动信息较多,会对后续叶片振动分析造成不利影响。
5 趋势项自适应拟合算法设计
假设原始叶尖定时信号为{yc},数据点数为N。本文提出的叶尖定时信号趋势项自适应拟合方法计算流程如图4所示,算法执行步骤如下:
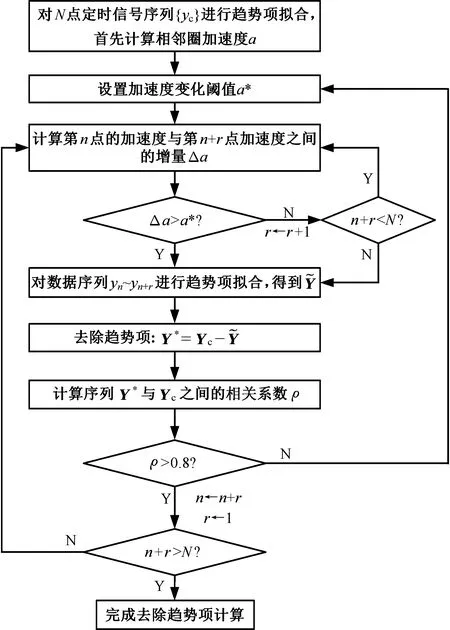
图4 自适应趋势项拟合算法Fig.4 Trend item fitted algorithm with adaptive
(1)计算相邻圈内的加速度序列an(n=1,2,…,N-1)。
(2)设置加速度变化阈值a*。
(3)计算an与an+r的相对增量Δa,并判断是否满足式(7),若不满足则转步骤(4);若满足则转步骤(5)。
(4)令r=r+1,若n+r
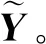
(6)根据式(12)计算叶片振动位移y*。
(7)根据式(13)计算yc与y*之间的相关系数ρ,若ρ<0.8,则转步骤(2);否则,转步骤(8)。
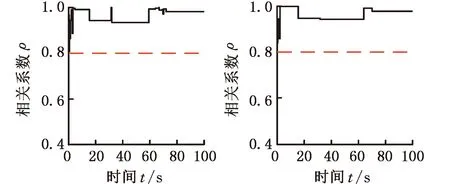
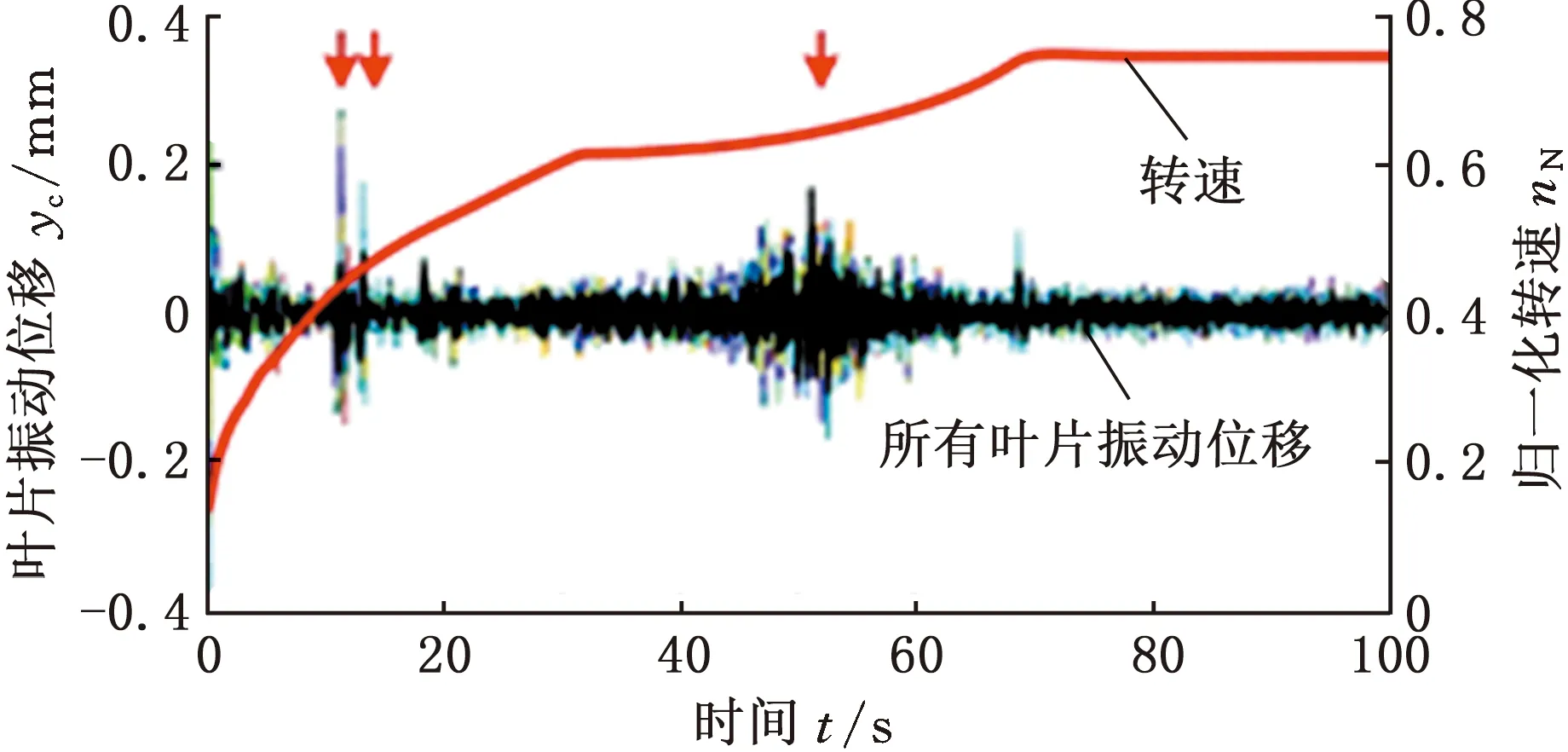
(8)令n←n+r,判断n是否小于N,若n 当相关系数小于0.8时,本文采取的调节加速度阈值a*的策略为:修正加速度阈值为原阈值的90%。然后基于新的加速度阈值重新确定拟合窗宽度,并进行趋势项拟合及拟合效果评价,重复以上过程,直至相关系数大于0.8为止,再进行下一段数据趋势项拟合。通过评价拟合效果来实现自适应拟合窗宽度调整,完成不同周期内趋势项拟合,实现自适应去除趋势项的目标。 采用叶尖定时测量方法对某型航空发动机高压压气机第1级叶片周向弯曲振动进行监测。航空发动机从启动至慢车过程中监测的叶尖定时信号,既是常规分析叶片同步共振最重要的数据段,同时由于该过程叶片运行流场环境瞬时多变,导致静态偏转变化复杂,所以也是定时信号趋势项拟合难度最大的一段数据。本文选取航空发动机启动至慢车过程中的定时数据,用于比较固定窗宽度拟合与自适应窗宽度趋势项拟合两种方法性能。航空发动机启动至慢车转速升转曲线及监测的叶片振动位移曲线如图5所示,由于受到叶片静态偏转影响,叶片振动位移均偏离零值水平线,对叶片振动参数准确辨识造成严重影响。 图5 试验转速曲线和叶片振动位移曲线Fig.5 The curve of the rotating speed and blade vibration displacement 首先采用固定窗宽度对图5中的叶片振动位移进行趋势项拟合。罗·罗公司叶尖定时测量技术专家RUSSHARD[26]给出的趋势项窗宽度经验值为200。本文为得到不同窗宽度拟合效果,分别设置4组拟合窗宽度参数,见表1。令多项式阶数m为1,即采用线性拟合,得到不同拟合窗宽度下1号叶片振动位移趋势项拟合结果,如图6所示。由拟合结果可以看出,随着拟合窗宽度增加,趋势项拟合对原始振动波形的破坏程度降低,过拟合程度得到改善。 表1 趋势项固定窗宽度拟合参数设置Tab.1 The parameter setting of trend item fitted with fixed window width (a)W=50 采用相关系数对趋势项固定窗宽度拟合效果进行评价,相关系数越大,则表明去除趋势项后的定时信号保留的振动信息越多。相关系数计算结果如图7所示,由计算结果可知,虽然随着拟合窗宽度增加,相关系数低于0.8的波形数据情况有所减少,但即使对于窗宽度为200和300的趋势项拟合,依然存在相关系数低于0.8的情况。因此,对于航空发动机启动至慢车阶段,由于叶片趋势项变化复杂,故固定窗宽度拟合很难保证趋势项去除前后的数据依然保持极度相关关系,即去除趋势项后的数据存在丢失部分振动信息的风险。 (a)W=50 (b)W=100 采用自适应窗宽度对同一枚叶片振动信号进行趋势项拟合,通常压气机试验过程采用加速度25 r/(min·s)进行升转,但由于整机启动至慢车数据段,升转加速度变化要远远大于压气机试验加速度,故本文设置的4组趋势项拟合参数加速度阈值a*较大,具体设置见表2。 表2 趋势项自适应拟合参数设置Tab.2 The parameter setting of trend item fitted with adaptive 设置多项式阶数m为1,4组趋势项自适应拟合结果如图8所示,分别对应表2中的4组参数拟合结果。由拟合结果可以看出,趋势项拟合窗是变宽度的,这是数据窗宽度自适应调整的结果。计算4组趋势项拟合结果的相关系数,如图9所示,可以看出4组相关系数在整个拟合数据段范围均大于0.8,证明本文提出的趋势项自适应拟合方法可完全保留原始振动信息,有利于后续叶片振动分析。 (a)a*=45 (a)a*=50 (b)a*=80 采用SG方法[39-40],设置平滑点数为33,平滑阶数为1,分别对两种方法第2组去除趋势项后的叶片振动信号进行平滑滤波。对固定拟合窗宽度为200的趋势项去除结果进行平滑滤波后的结果如图10a所示,处理后的叶片振动曲线有3处较为明显的振动响应(图10a中红色箭头所示)。对自适应窗宽度第2组趋势项去除结果进行平滑滤波后的结果如图10 b所示,处理后的叶片振动曲线有6处较为明显的振动响应(图10b中红色箭头所示)。与预处理前的叶片振动位移曲线进行比较,虽然两种趋势项拟合方法均可有效去除趋势项,将叶片振动位移曲线平移至零值水平线位置,但是与固定窗宽度趋势项拟合方法相比,自适应窗宽度拟合方法对原始波形破坏程度较小,明显保留了更多的原始振动信息,可为后续高精度叶片振动参数辨识提供更高质量的定时数据。 (a)W=200 本文提出了趋势项自适应窗宽度拟合方法,通过计算趋势项去除前后定时信号相关系数来对趋势项拟合效果进行评价,并以相关系数是否达到0.8为阈值,实现自适应调节窗宽度目的。采用航空发动机高压压气机启动至慢车过程叶尖定时数据进行验证,结果表明,与固定窗宽度趋势项拟合方法相比,自适应窗宽度拟合可保证趋势项去除前后的数据始终保持极度相关,即在趋势项去除的同时,完全保留原始振动信息,能够为后续叶片振动分析提供高质量的定时数据,对于实现高精度叶片振动参数辨识具有重要意义。6 试验验证
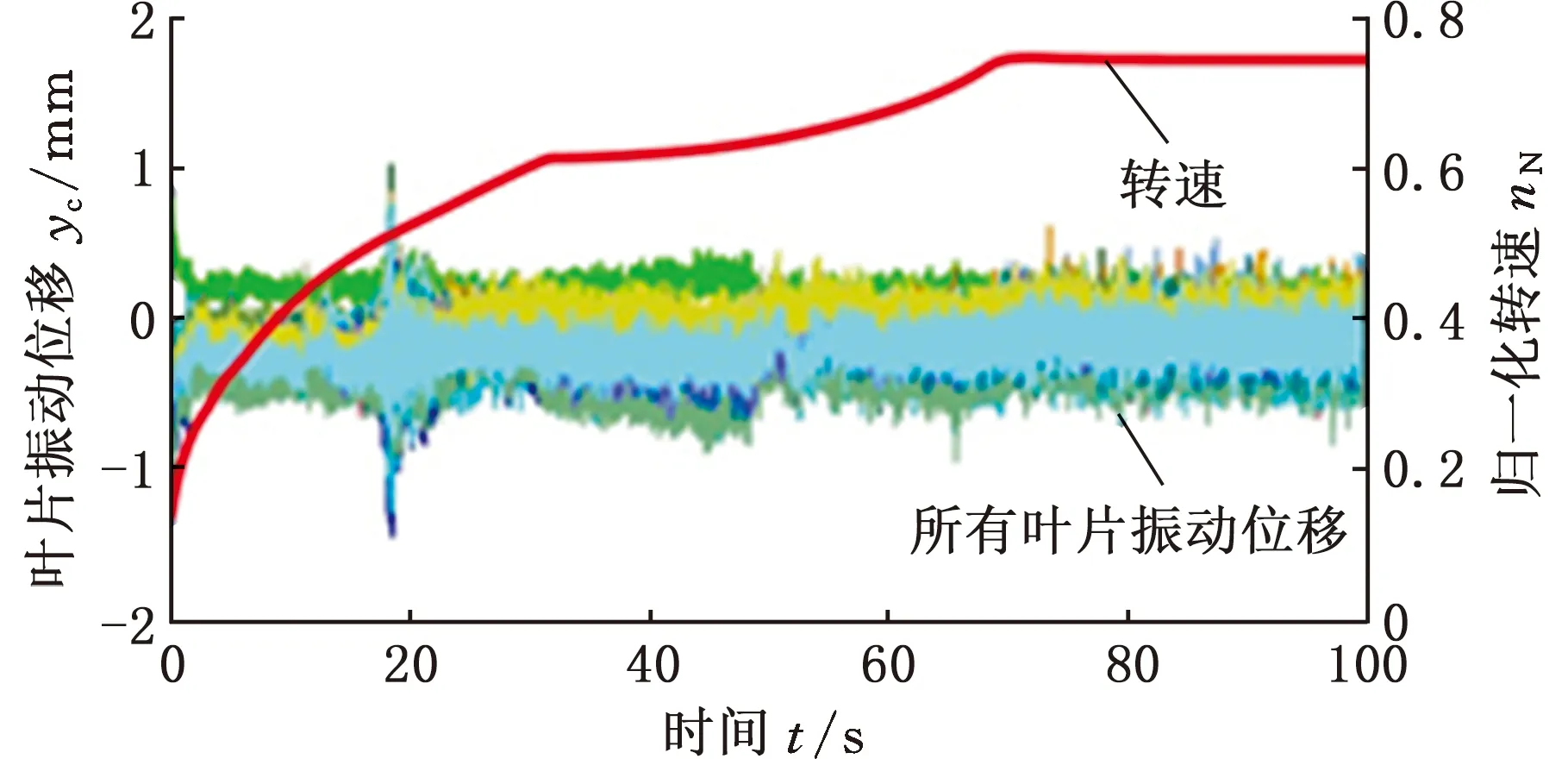

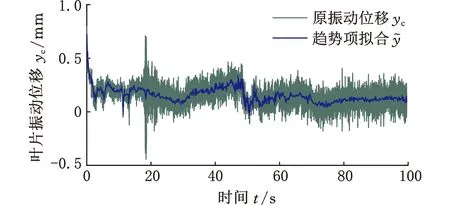
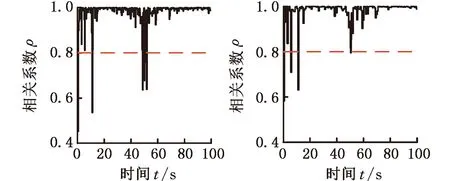


7 结论

