含时摩擦系数和扩散调控布朗粒子的异常输运
由曌婷,罗玉辉,2,杨凤藻
(1.昆明理工大学 理学院,云南 昆明 650500;2.昭通学院 物理与信息工程学院,云南 昭通 657000)
近年来,远离平衡态的异常输运现象[1-2]激起了很多学者的兴趣,得到了广泛的关注.该现象中的棘轮效应[3-4]和负迁移现象[5-7]被广泛研究.棘轮效应,其特征是在没有外部扰动的情况下,平均的有向运动已经是非零的,并且在整个正、负的静力范围内不改变其方向.在过去的几十年里,这一输运现象已经被研究在各种系统中[8-10].此外,负迁移现象是一种看似矛盾的运动,其粒子的运动方向与一个小的外力方向相反,这与热力学第二定律相违背,热力学第二定律[7,11]指出:当系统处在热力学平衡时,负迁移发生是不可能发生的.然而,当一个时间周期力驱动一个系统,使得系统远离平衡,负迁移现象的发生成为可能.这一现象已经在实验验证[12]和理论预测[13-14]被研究.
近二十年来,棘轮效应和负迁移等异常现象被广泛研究[7,15-17].可以注意到,在以往的大多研究中把摩擦系数假设为是一个常数.然而,众所周知,在真实系统中,摩擦研究起来是非常复杂的,理论[18-20]和实验[21]的研究都证明了摩擦系数不是一个常数,而是随某些参数而变化的,例如它会随着位置、速度[22]、温度[23]、时间[24]而发生变化.近来,大量的研究[25-26]证明了含时的摩擦在布朗粒子的运动中起着极其重要的作用.那么,含时摩擦系数是如何影响惯性布朗粒子的输运呢?推测,它将显著地影响粒子的输运行为(比如,棘轮效应,负迁移现象和异常扩散).此外,扩散系数在一定程度上受到初始扩散系数的影响,从而对系统产生影响.因此,在上述讨论的推动下,惯性布朗粒子在含时摩擦系数和初始扩散系数的对称周期势中的粒子输运问题仍然是一个悬而未决的问题,也是本研究的主题.
1 模型
考虑一个惯性布朗粒子受到时间周期力和外部偏置力的驱动在空间周期对称系统中的运动.其中振幅为a,角频率为ω的时间周期力使得系统处于非平衡状态.因此,粒子的欠阻尼动力学是由阻尼系数γ(t)和热涨落导致的含时的扩散系数d(t)引起的含时扩散的朗之万方程建模的,即
(1)
其中撇表示x的导数.η(t)是零均值的一个高斯白噪声<η(t)>=0,不同时刻之间存在δ关联,即<η(t)η(t′)>=δ(t-t′).V(x)周期为L的对称周期势V(x)=V(x+L),势垒高度ΔV,显正弦形式为:
(2)
γ(t)代表含时的阻尼系数[26],即
(3)
其中γ0是初始时刻的阻尼系数γ0=γ(0),此外,它包含了含时的温度T(t),表示形式为
(4)
这里的扩散的幂律指数α≥0,T0是初始温度T0=T(0),τ0表示为温度衰减的时间特征.τ0的值越大,温度下降得越慢.因此,在这里我们考虑由热涨落导致的含时的扩散系数[26],即
(5)
其中d0是初始扩散系数d0=d(0).因此,在引入含时的阻尼系数和扩散系数,方程式(1)可重写为:
(6)
在本文中,固定参数振幅a=4.2,角频率ω=4.9,周期L=1,初始摩擦系数γ0=1,势垒高度ΔV=1.
一般地,朗之万方程(6)对应的福克-普朗克方程是无解的.因此,为了研究相关的异常输运的现象,必须使用数值模拟方法.文中采用步长为Δt=10-2的精确的欧拉算法.速度和位移的初始条件是满足在区间[-1,1]上的均匀分布的,所有的平均值是通过500条不同的轨道得到的,每条随机轨道演化迭代次数为107次.此外,通过平均速度、平均轨道、均方位移以及含时的扩散系数来研究异常输运的特性.
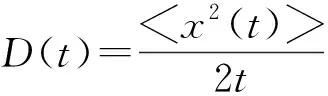
2 数值模拟结果
在图1中,描述了对于不同的初始扩散系数D0,v作为偏置力f的函数,当f=0时,随着初始扩散系数D0的增大,平均速度⟨v⟩也在增大,也就是说,随着初始扩散系数D0的增大,棘轮效应在增强.此外,我们发现当f≠0时,随着初始扩散系数D0的增大,平均速度v的值也是在增大的.对于图2,当无偏置力(f=0),初始扩散系数D0在增大时,平均轨道随着时间t的增大而增大,换句话说,平均速度随着初始扩散系数D0的增大而增大.这与图1结果相一致.总之,初始扩散系数D0增强了棘轮效应.
图3中,描述了对于不同的温度衰减的时间特征τ0,v作为偏置力f的函数,当f=0时,随着温度衰减的时间特征τ0的增大,平均速度v在减小,也就是说,随着温度衰减的时间特征τ0的增大,棘轮效应在减弱.此外,我们发现当f≠0时,随着温度衰减的时间特征τ0的增大,平均速度v的值反而是在减小的.对于图4,当无偏置力(f=0),温度衰减的时间特征τ0在增大时,平均轨道随着时间t的增大而减小,换句话说,平均速度随着温度衰减的时间特征τ0的增大而减小.这与图3结果相一致.简言之,温度衰减的时间特征τ0减弱了棘轮效应.
图5中,描述了对于不同的扩散的幂律指数α,v作为f的函数,当f=0时,扩散的幂律指数α较小(取α=0.5)时,平均速度为-0.02,显然棘轮效应出现,但是当扩散的幂律指数较大(取α=1.0)时,随着偏置力f的变化,扩散的幂律指数在0附近波动,即平均速度几乎为零,换句话说,棘轮效应消失,然而当扩散的幂律指数更大(取α=1.5)时,从图5中的小图很显然发现有负迁移现象发生.图6刻画了当无偏置力(f=0)时,平均轨道随时间的变化的曲线,扩散的幂律指数α较小(取α=0.5)时,随着时间t的增大,平均轨道是负的,即平均速度是负值,但是随着扩散的幂律指数α的增大,平均轨道趋近于零,即平均速度为零.这与图5相吻合.
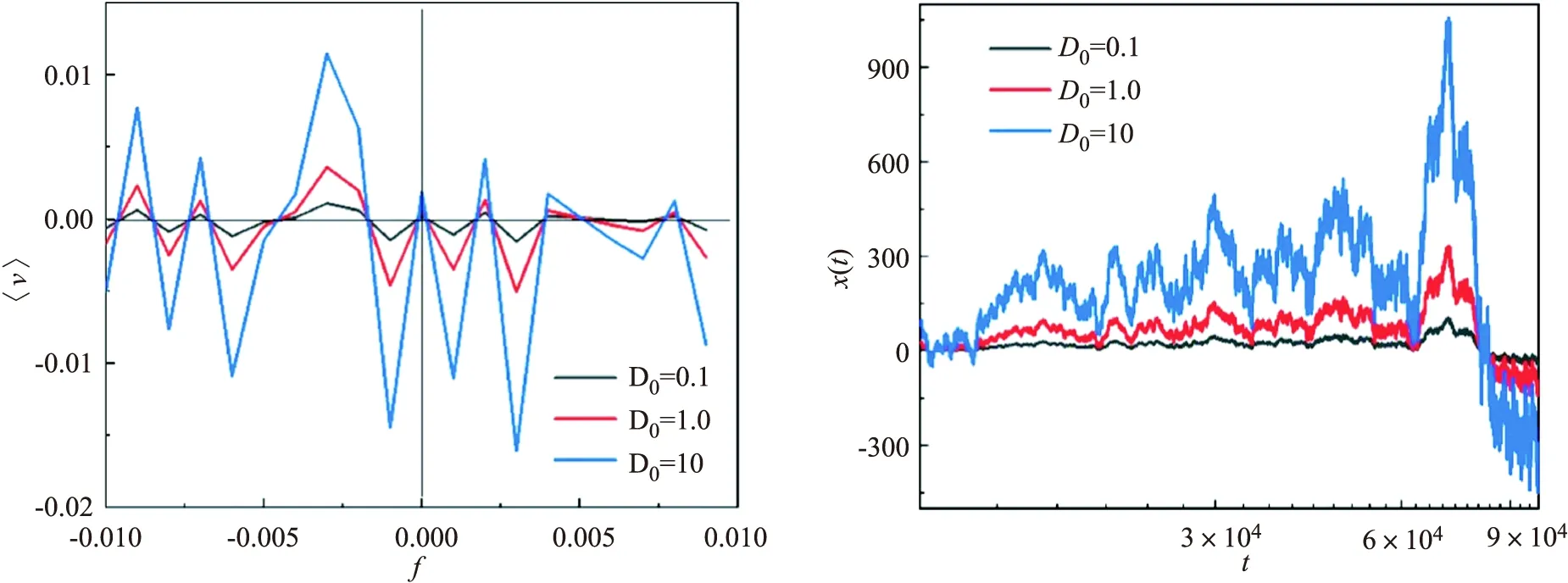
τ0=10,γ0=1,α=1.5 τ0=10,γ0=1,f=0,α=1.5 图1 平均速度随偏置力f变化的曲线 图2 平均轨道随时间t变化的曲线

D0=10,γ0=1,α=1.5 D0=10,γ0=1,f=0,α=1.5图3 平均速度随偏置力f变化的曲线 图4 平均轨道随时间t变化的曲线
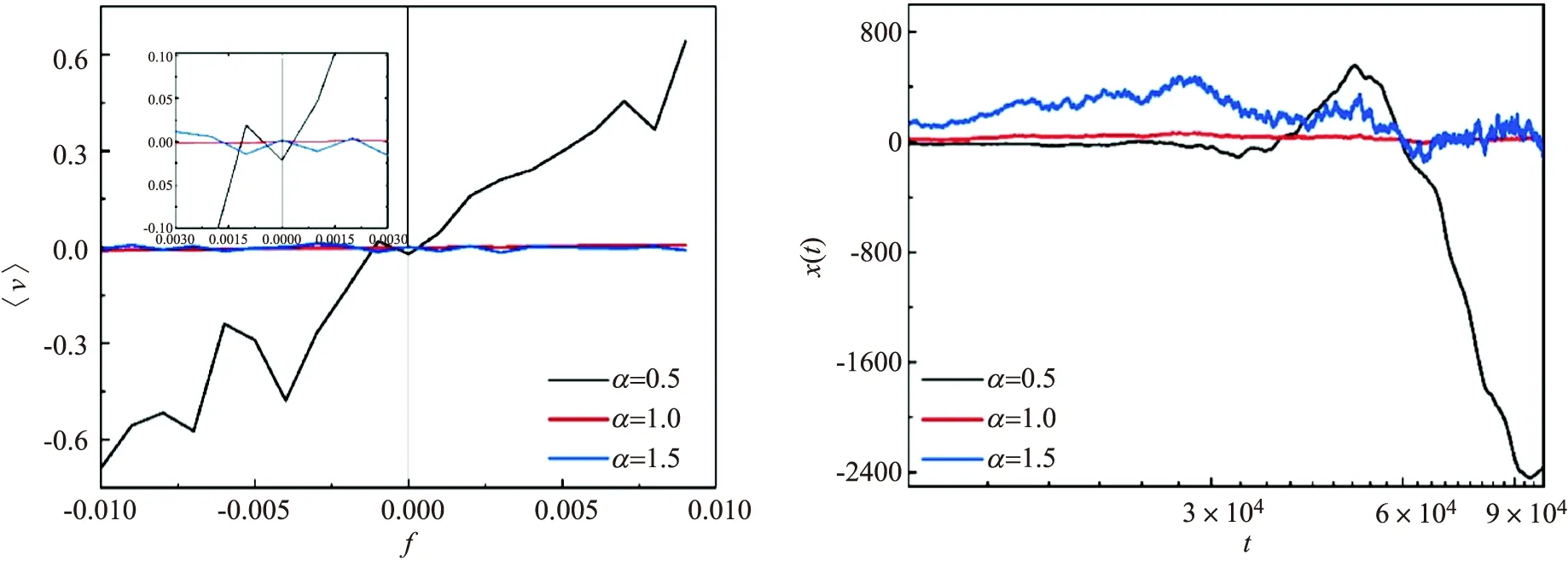
τ0=10,γ0=1,D0=10 τ0=10,γ0=1,D0=10,f=0图5 平均速度随偏置力f变化的曲线 图6 平均轨道随时间t变化的曲线
图7中,描述了均方位移和依赖时间的扩散系数随时间变化的曲线图.图7(a)~ (c),通过均方位移 ⟨x2(t)⟩∝tβ来研究粒子的扩散,对所得到的结果进行线性拟合, 0<β<1是亚扩散,β=1是正常扩散, 1<β<2是超扩散,β=2是弹道扩散,β>2是巨扩散.为了更好地理解粒子的扩散性质,我们也呈现了依赖时间的扩散系数如图7(d)~(f).从图7(d)中发现,当D0=0.1时,D(t)在短时间内随着时间的变化先减小,然后恒定不变,最后增大,即粒子先经历亚扩散,然后正常扩散,最终超扩散;当初始扩散系数较大时(如D0=1,10)时,D(t)在短时间内随着时间的变化一直增大,即粒子经历超扩散.此外,随着初始扩散系数D0增大,扩散系数也在增大.图7(e),当τ0=10时,D(t)在短时间内随着时间的变化一直增大,即粒子经历超扩散;当温度衰减的时间特征τ0较大(如τ0=100,1 000)时,D(t)在短时间内随着时间的变化先增大,然后恒定不变,最后增大,即粒子先经历超扩散,然后正常扩散,最终超扩散.此外,随着温度衰减的时间特征τ0增大,扩散系数在减小.从图7(f),我们可以发现,当α=0.5时,D(t)在短时间内随着时间的变化先增大,后减小,最后增大,即粒子先经历超扩散,然后亚扩散,最终巨扩散;当α=1.0时,D(t)在短时间内随着时间的变化先增大,然后恒定不变,即粒子先经历超扩散,然后正常扩散;当α=1.5时,D(t)在短时间内随着时间的变化一直在增大,即粒子经历超扩散.
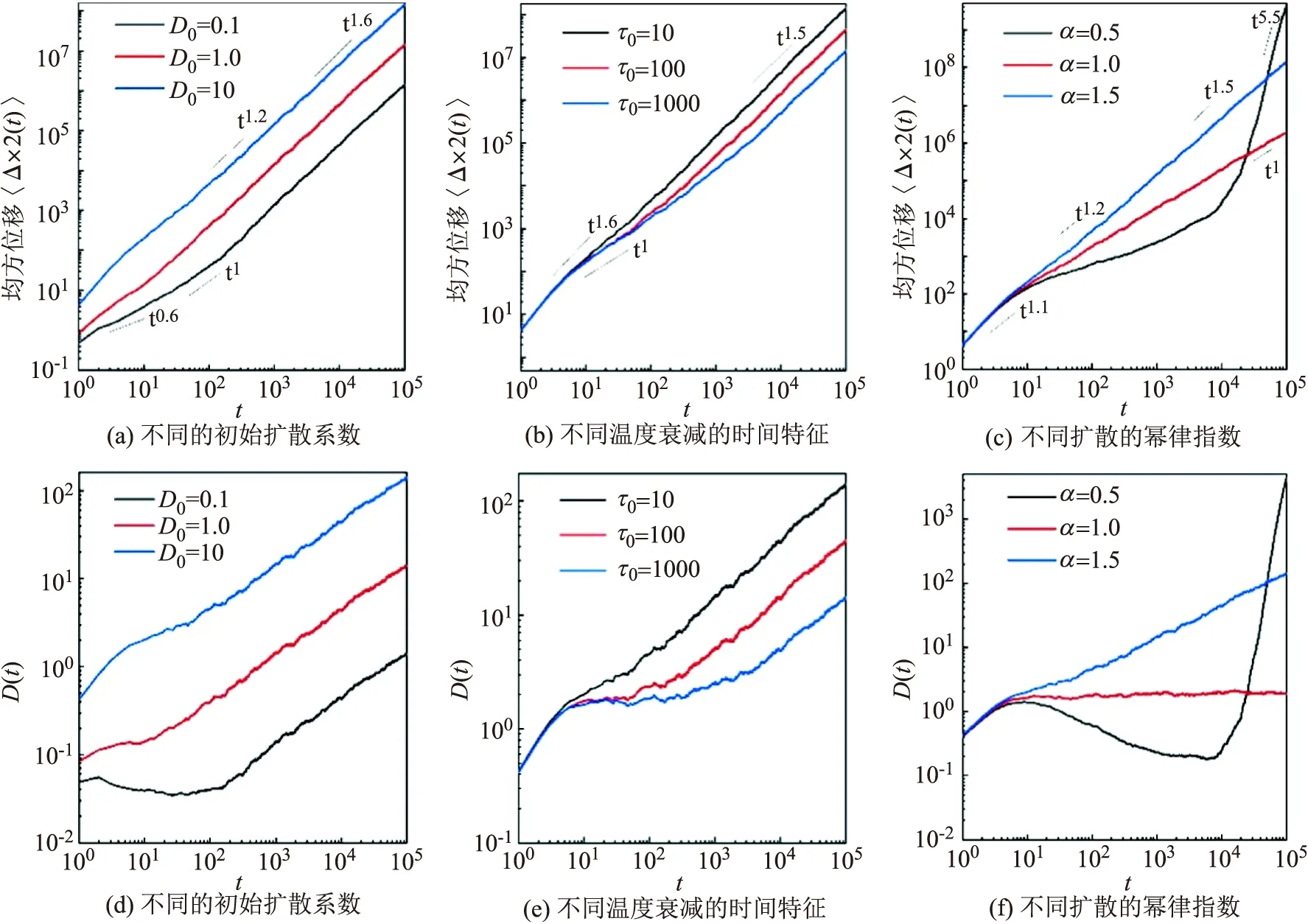
图7 均方位移(上)和依赖时间的扩散系数(下)随时间t变化的曲线.
3 结语
借助于数值模拟研究了在空间周期对称系统中惯性布朗粒子在外部偏置力和时间周期力的驱动下的输运问题,进而讨论了含时的摩擦和扩散系数对粒子异常输运的影响.研究结果表明:随着初始扩散系数D0的增大,扩散系数在增大,棘轮效应在增强.然而随着温度衰减的时间特征τ0的增大,扩散系数在减小,棘轮效应在减弱.当扩散的幂律指数α较小时,有棘轮效应现象出现,但是当扩散的幂律指数较大时,棘轮效应消失,然而当扩散的幂律指数更大时,负迁移现象出现.此外,不同的初始扩散系数、温度衰减的时间特征、扩散的幂律指数对应于不同的扩散.我们的发现可能应用于粒子的分类[14,27]、癌细胞的分离[28-29]、分子马达的控制[30]以及其它微观现象.

