地震作用下RC构件耗能能力的计算方法研究

刘哲锋，郑 潇，王玉奎

(1. 长沙理工大学土木工程学院，湖南，长沙 410004；2. 湖南城市学院土木工程学院，湖南，益阳 413049)

基于能量的抗震设计认为，在地震荷载作用下，输入到结构的能量表现为弹性应变能、结构动能、阻尼耗能和滞回耗能，并使结构产生损伤、甚至破坏[1−3]。为避免结构体系出现严重失效，地震输入能量需小于结构总耗能能力[4−5]。由于结构动能和弹性应变能可储存并且能相互转化而不参与能量耗散，因此地震输入能量主要通过阻尼耗能和滞回耗能耗散，但在实际工程中发现，阻尼耗能仅占很小一部分，故结构的失效程度主要取决于结构自身滞回耗能的能力高低[6−7]。

Housner[8]在《结构抗震的极限设计》一书中提出了能量抗震设计方法的概念，认为地震对结构的输入能量是仅与结构质量和周期有关的定值；Park和Ang等[9−10]对构件最大变形和滞回耗能对构件的影响进行综合考虑，提出钢筋混凝土(RC)构件的双参数破坏模型，但该模型未考虑地震持时的影响，且组合参数β离散型较大；基于足量RC构件在回归统计下的分析结果，得到损伤指数中的比例参数β，即该损伤模型可以对不同变幅加载历程下RC构件的破坏程度进行较为准确的定义，但对可修复状态下构件损伤的定义还缺乏足够的理论和试验依据[11−15]；Erberik等[16 −17]通过对17根RC梁构件进行往复滞回试验，建立了耗能能力的常幅衰变规律与变幅衰变规律之间的联系，创造性地提出了RC梁构件变幅滞回耗能能力的确定方法，但由于研究是针对既有建筑中以光圆钢筋为纵筋的混凝土构件，因此结论的应用范围有限；Poljansek等[18]利用既有RC矩形柱的滞回试验数据库，基于统计分析研究RC柱的滞回耗能能力与损伤后变形能力的主要影响因素，由于数据库中的加载规则趋于一致，因此研究事实上避免讨论了加载历程不同所造成的影响；刘哲锋等[19−20]对22根RC构件采用稳态变幅加载和任意变幅加载，分析了加载位移历程、配箍率和配筋率的变化对RC构件滞回衰变规律的影响，提出了变幅滞回条件下耗能能力的计算方法，但所依据的数据量有限，且未考虑轴向力、剪跨比、混凝土强度等设计参数对计算结果的影响规律，应用范围有限。

本文依据文献[20]中18根稳态变幅加载的RC构件，通过对试件衰减指数发展曲线的分析，提出D-n曲线平移假设并对原耗能能力计算方法中的相关参数进行优化，使耗能能力计算结果更为准确。选取了PEER数据库中80根弯曲破坏、有轴力、剪跨比大于2的对称配筋矩形截面RC构件，用优化后的计算方法进行耗能评估，评估结果表现出较好的准确性和适用性。

1 变幅滞回条件下RC构件耗能能力估算模型

1.1 稳态变幅滞回条件下半滞回耗能能力估算

对半滞回的定义为：连续两个荷载零点间的滞回曲线，即一个滞回环被位移横轴分为上、下2个半滞回环(图1)。

RC构件第k个半滞回的耗能能力衰减指数DE,k定义为：

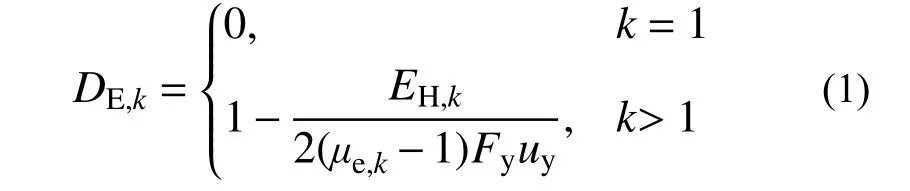
式中： EH,k为第k个半滞回耗散的滞回能量，如图1黑色实线与坐标横轴所围面积； 2(μe,k−1)Fyuy为理想无损状态下RC构件在相同滞回过程中的滞回能量，如图1两个虚线平行四边形面积。Fy为屈服荷载；uy为屈服位移；μe,k为第k个半滞回的平均名义半滞回幅值，其表达式为：

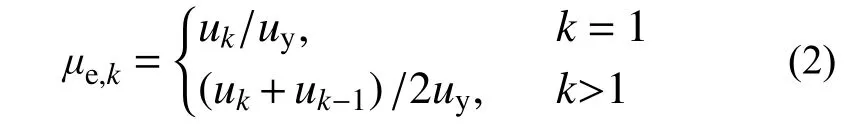
式中，uk为第k个半滞回的位移幅值。

研究表明，在稳态变幅滞回条件下，RC构件耗能能力衰减指数整体上呈增加趋势，但滞回位移幅值的变化导致这一趋势呈现规律性的不连续，此外不同位移加载历程对RC构件耗能能力衰减具有显著的影响。文献[20]根据上述规律提出了稳态变幅滞回条件下衰减指数 DE,k的估算方法：

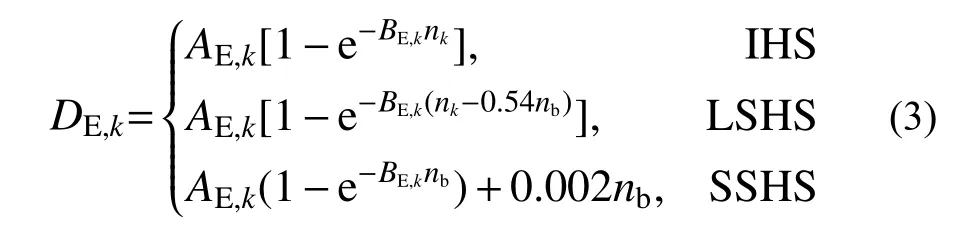
式中：IHS表示初始滞回阶段；LSHS表示后续大滞回阶段；SSHS表示后续小滞回阶段；nk为前k−1个半滞回的名义累积滞回耗能：

nb为第k个半滞回所在常幅滞回阶段开始时的名义累积滞回耗能。参数 AE,k和 BE,k按下式计算：

式中，ρsv为配箍率。

稳态变幅滞回条件下RC构件半滞回耗能计算公式为：

1.2 任意变幅滞回条件下半滞回耗能能力估算

对任意变幅加载RC构件的位移历程进行稳态化处理：将小于1的μe,k值去除(这类半滞回所耗散的能量通常很小，可以忽略)，并对具有相近μe,k值的连续半滞回采用均值化的办法将其转化为常幅滞回阶段，即：

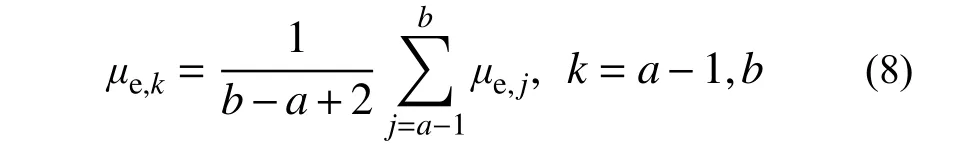
判断μe,k值是否相近，需同时满足以下两式：

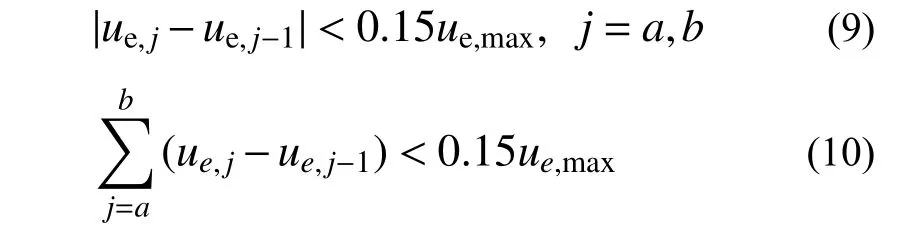
基于所得的常幅滞回阶段，利用如图2所示的稳态变幅滞回RC构件耗能计算流程估算其耗能。

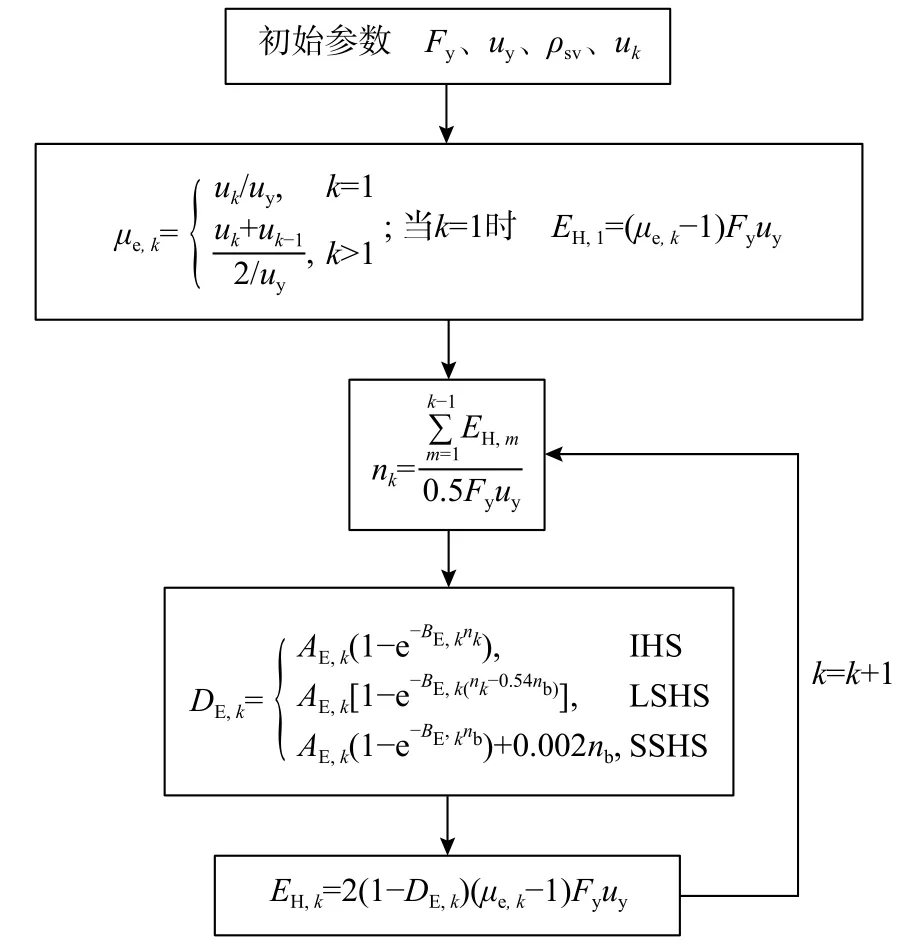
图2 稳态变幅滞回条件下半滞回耗能计算方法流程Fig.2 Flow chart of estimation method for half-cycle hysteretic energy dissipation under steady variable amplitude hysteretic process

2 模型的优化

2.1 各滞回阶段衰减拟合模型

限于篇幅，仅列出文献[20]中试件S7、S8、S9分别在3种稳态变幅加载模式下耗能能力衰减指数 DE,k随名义累积滞回耗能nk的变化趋势(以下简称D-n曲线)，如图3所示。由图可知，不同常幅加载阶段的D-n曲线间形成间断点，对于初始滞回阶段，D值随名义累积滞回耗能的增加而由0向1单调增长，增长的趋势逐渐变缓；对于后续大滞回阶段，D值由一个低点再逐渐增大；对于后续小滞回阶段，D值上升到一个高点，且数值维持稳定。

图3 3种稳态变幅加载模式下的试件D-n曲线Fig.3 D-n curves for specimens under three steady variable amplitude loading patterns

对于初始阶段试件滞回耗能能力的衰变规律，采用试件初始滞回阶段的D-n曲线予以说明。根据曲线以零点为起始点，随横坐标值的增加斜率逐渐变小且最终趋零的特点，提出半滞回耗能能力衰减模型：

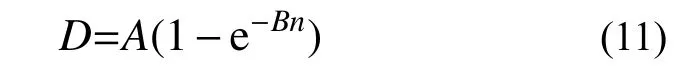
模型中D值与拟合参数A、B的关系，如图4所示。

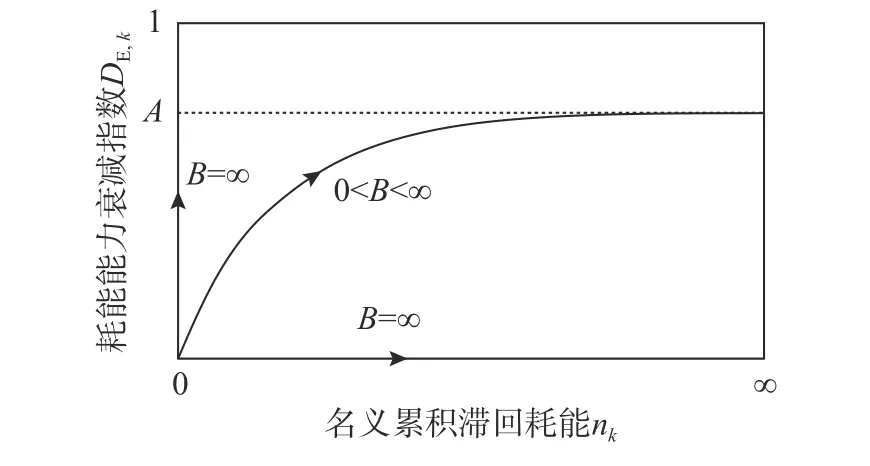
图4 衰减模型特征参数A和B的物理意义Fig.4 Exponential recovery formulation with two parameters A and B

A值为试件以某幅值进行常幅滞回时，其耗能能力衰变至稳定时的D值。A值越大，表明构件达到滞回稳定时，耗能能力的衰减越严重，残余耗能能力越低。而B值大小则体现耗能衰减的快慢，B值越大，D-n曲线越陡峭，构件耗能能力衰变至稳定的过程越为迅速，衰变稳定时耗散的名义滞回能量越少。图3中的实线为式(11)对试件初始D-n曲线的拟合结果。

对于后续阶段试件滞回耗能能力的衰变规律，采用试件后续滞回阶段的D-n曲线予以说明。以平均名义半滞回幅值相等为原则，将同类型试件在3种稳态变幅加载模式下的D-n曲线重新构图，即μe,k值相等的常幅滞回阶段的D-n曲线并入一张图中，图3在重新构图后成为图5。

由图5可知，某后续滞回阶段D-n曲线，与μe,k值相等的初始滞回阶段D-n曲线在形态上具有关联性：对于后续小滞回阶段，其D-n曲线位于初始D-n曲线的上方，曲线呈水平或点状；对于后续大滞回阶段，其D-n曲线位于初始D-n曲线的右侧，曲线形态相近。

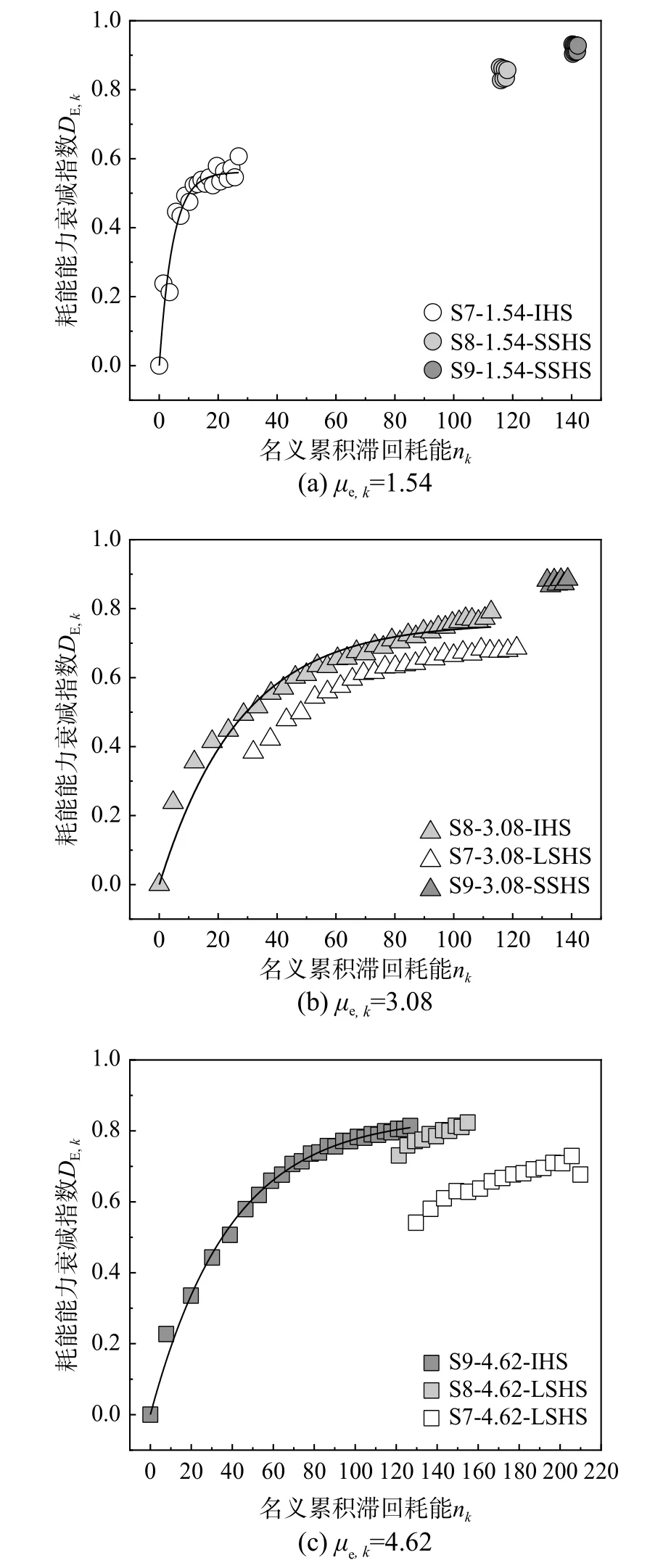
图5 按平均名义半滞回幅值相等原则构图的试件D-n曲线Fig.5 D-n curve of the specimen constructed according to the principle of equal average nominal half hysteresis amplitude

基于此规律，提出如图6所示的D-n曲线平移假设：某后续滞回阶段开始时的名义累积滞回耗能为nb，若该后续阶段为后续大滞回阶段(图6(a))，其D-n曲线轨迹由延性相同的初始D-n曲线向由右平移x0获得，横坐标起点为nb，则半滞回耗能能力衰减模型变形公式为式(12)；若为后续小滞回阶段(图6(b))，其D-n曲线为水平直线，起始点为延性相同的初始D-n曲线向上平移y0后与n=nb的交点，则半滞回耗能能力衰减模型变形公式为式(13)。

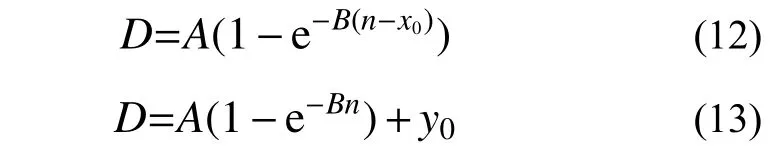
图6 稳态变幅加载下后续滞回阶段D-n曲线平移模型Fig.6 The estimation method of D-n curve in subsequent hysteresis stage

2.2 模型中拟合参数的修正

参数A、B、x0、y0是通过对各试件各滞回阶段D-n曲线进行非线性拟合得到的。对于初始滞回阶段： x0=0,y0=0，利用式(11)对其D-n曲线进行拟合，得出A、B；对于后续大滞阶段：x0≠0,y0=0，利用式(12)对其D-n曲线进行拟合，得出A、B、x0；对于后续小滞回阶段： x0=0,y0≠0，由于其D-n曲线数据点集中分布，未呈现明显的规律性趋势，故将A、B视为已知，并用同类型试件中具有相等μe,k值的初始滞回阶段的A、B值代替，利用式(13)对其D-n曲线进行拟合，得出y0。表1～表3给出了文献[20]中18个稳态变幅加载试件的A、B、x0、y0值。

表1 第Ⅰ常幅滞回阶段Table1 The first normal amplitude hysteresis stage

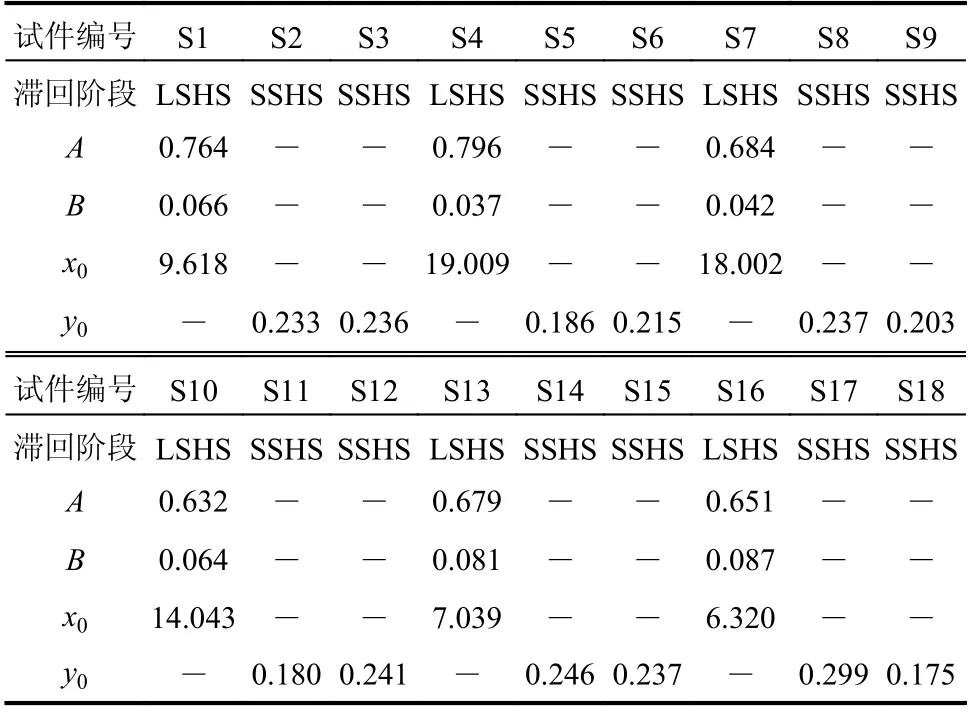
表2 第Ⅱ常幅滞回阶段Table2 The second normal amplitude hysteresis stage

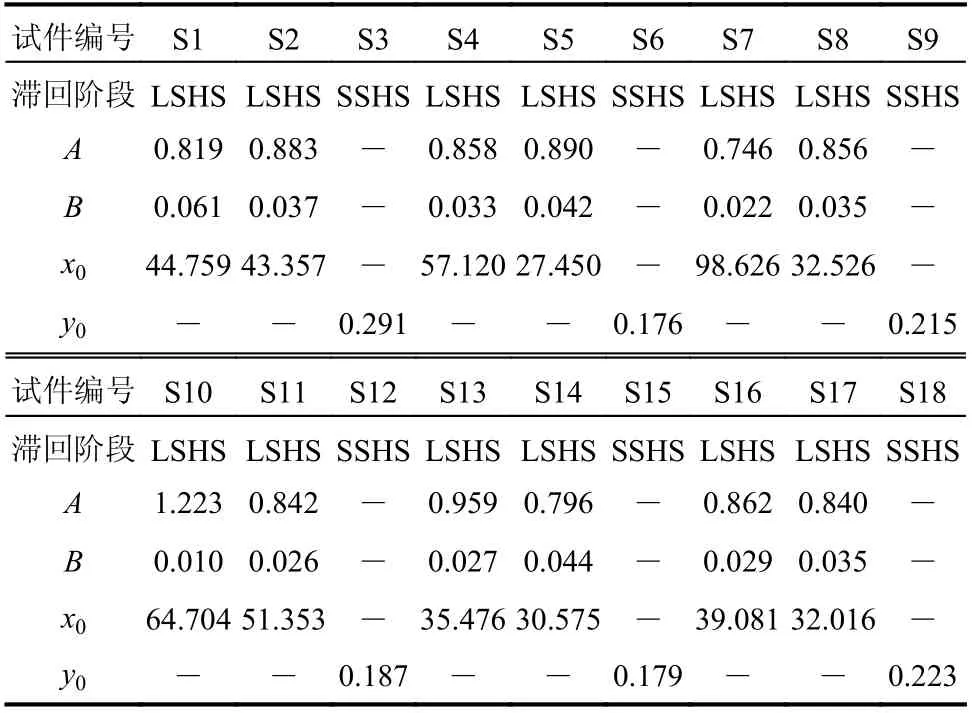
表3 第Ⅲ常幅滞回阶段Table3 The third normal amplitude hysteresis stage

参数A与平均名义半滞回幅值的关系见图7。

图7(a)中不同配筋率的数据点用不同符号区分，参数A随μe,k增大而增大，但受配筋率影响不明显。在图7(b)中不同配箍率的数据点用不同符号区分，配箍率对µ-A关系没有显著影响。因此忽略配筋参数对µ-A关系的影响，拟合结果在图7(b)中用黑色实线表示，式(14)是得到的拟合函数。

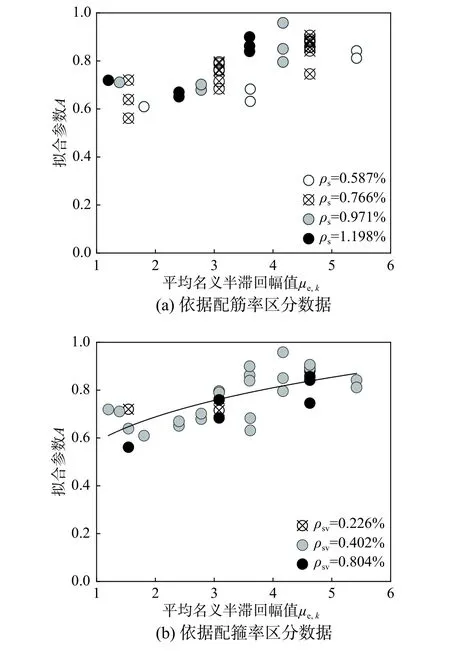
图7 平均名义半滞回幅值与A的关系Fig.7 Relationship ofμ e ,k with A

参数B与平均名义半滞回幅值的关系如图8所示。

在图8(a)中不同配筋率的数据点用不同符号区分，参数B随μe,k的增大而减小，而配筋率不会使B值呈现规律性变化。在图8(b)中不同配箍率的数据点用不同符号区分，增加配箍率会导致B值降低。综合考虑μe,k和配箍率对参数B值的影响，在图8(b)中，ρsv=0.226%、ρsv=0.402%和ρsv=0.804%的数据拟合结果分别用虚线、灰线和黑线表示，式(15)是得到的拟合函数。

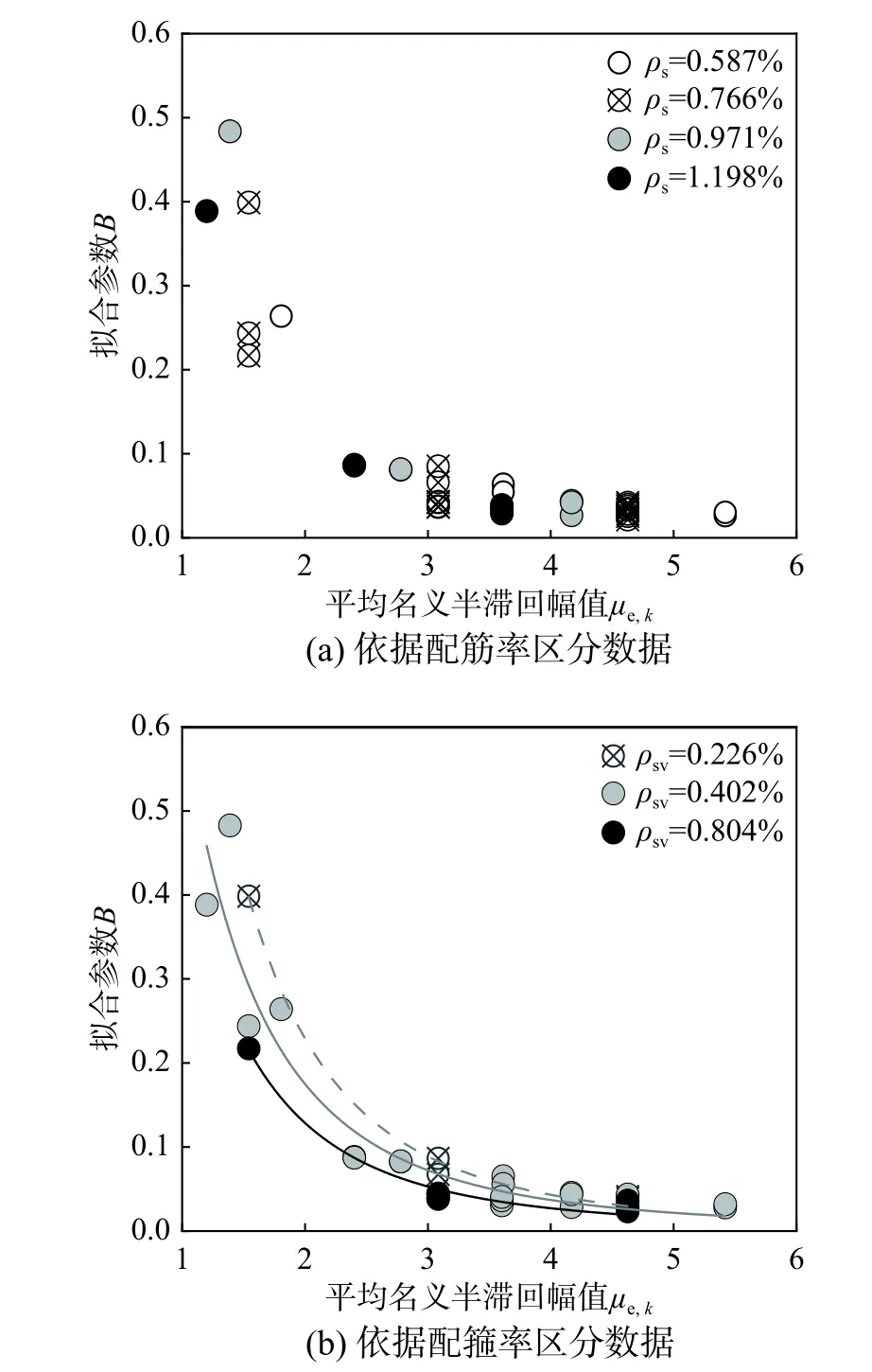
图8 平均名义半滞回幅值与B的关系Fig.8 Relationship ofμ e ,k with B

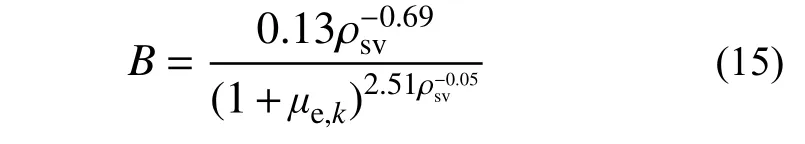
x0、y0与nb的关系如图9(a)、图9(b)所示。

图9 平移量与名义累积滞回耗能的关系Fig.9 Relations of two translations with nb

基于x0和y0的{物理意义，用过原点的线性拟合：

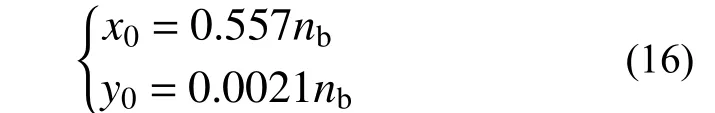
根据式(11)～式(13)、式(16)，在试件稳态变幅加载历程中，不同滞回阶段耗能能力衰减指数D的表达式为：

式中： AE,k和 BE,k分别由修正后的式(14)、式(15)确定；nk和nb均可按式(4)确定。

3 计算方法评估

为便于描述滞回耗能试验值与估算值的相关性，引用统计学的皮尔逊相关系数，通过耦合度寻找与试件半滞回耗能和累积滞回耗能所各自对应的趋势，以此对耗能能力计算方法的准确性进行评估。该系数可以描述两个变量间联系的紧密程度，度量其相关性，用r表示，其值介于−1与1之间，计算公式为：

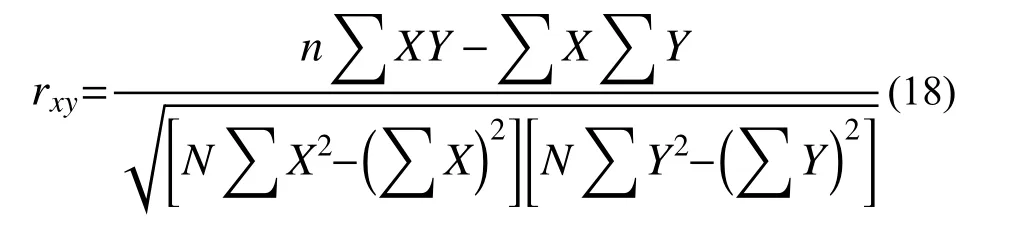
式中：n为样本量；X、Y分别为两个变量的观测值。一般定义：0.8＜r≤1.0极强相关、0.6＜r≤0.8强相关、0.4＜r≤0.6中等程度相关、0.2＜r≤0.4弱相关、0.0≤r≤0.2极弱相关或无相关。

3.1 优化模型与传统模型耗能对比评价

基于文献[20]中22根对称配筋矩形截面RC构件，利用估算模型对其计算半滞回耗能、累积滞回耗能，并与试验耗能进行比较。

将22根RC构件在两种模型下半滞回耗能的计算结果汇总放入以试验半滞回耗能值为横坐标、估算半滞回耗能值为纵坐标的坐标系中，如图10所示，其中N为22根试件半滞回总数，r为试验值与估算值之间的皮尔逊相关系数。由图可知，优化模型相比传统模型能使半滞回耗能试验值与估算值的相关系数更接近于1。

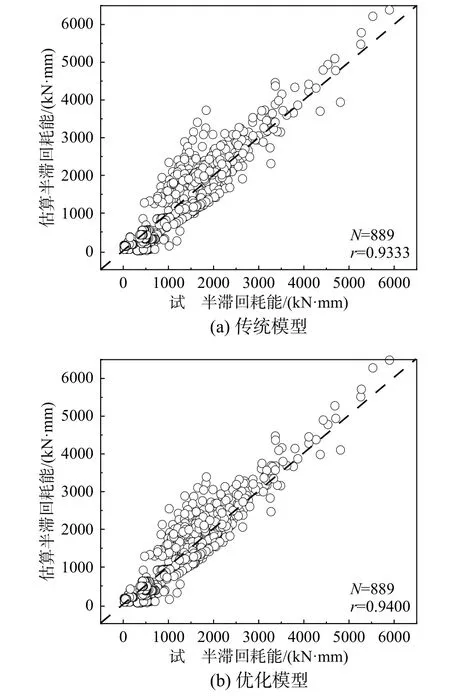
图10 22根RC构件在2种模型下半滞回耗能估算Fig.10 Estimation of semi-hysteretic energy consumption of 22 RC specimens under two models

图11详细展示了22根RC构件试验累积耗能、传统模型估算累积耗能和优化模型估算累积耗能3者之间的量级关系。

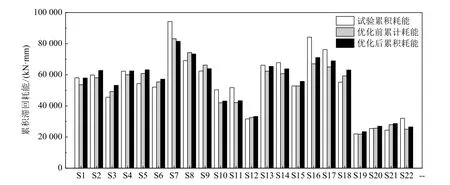
图11 22根RC构件累积滞回耗能试验值和估算值分布Fig.11 Distribution of experimental and estimated cumulative hysteretic energy consumption of 22 RC specimens

图12显示了22根RC构件在2种模型下累积滞回耗能的估算误差，其中Mean为估算误差平均值，SD为误差值标准差。由图可知，当用优化模型进行计算时，估算误差的平均值和误差值的标准差均减小。

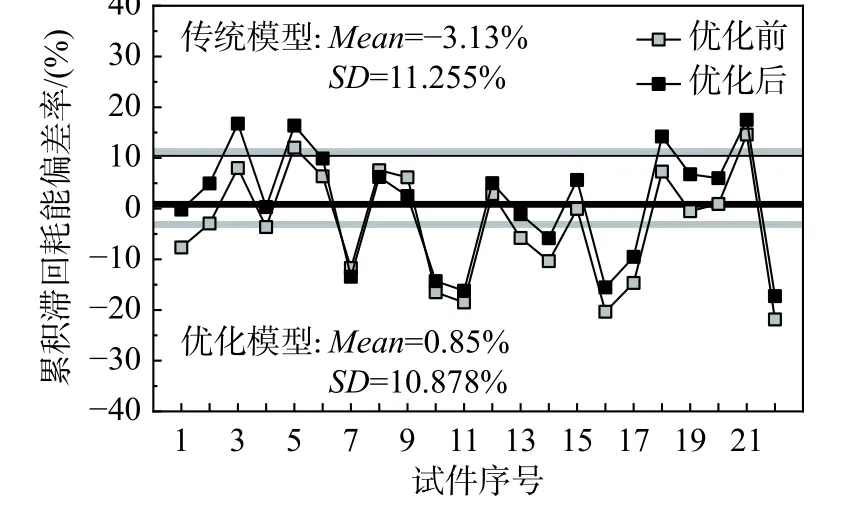
图12 22根RC构件在两种模型下累积滞回耗能估算误差Fig.12 Estimation error of cumulative hysteretic energy consumption of 22 RC specimens under two models

3.2 公共来源试件耗能评价

本文在美国太平洋地震工程研究中心(PEER)数据库中通过以下条件检索：1)有轴力；2)矩形截面对称配筋；3)剪跨比大于2；4)弯曲破坏，并经筛选得到80个试件样本，其中加载模式为稳态变幅加载的试件46个、标准试验加载17个、任意变幅加载17个，具体设计参数见附录。对其进行半滞回耗能和累积滞回耗能估算。

限于篇幅，仅列出6根试件半滞回耗能的计算结果，如图13所示，图中虚线表示过原点且斜率为1的位置，位于该虚线上的数据点表示其试件半滞回耗能试验值与估算值相等。由图可知，数据点基本围绕该虚线分布，且经式(18)计算得出6根试件的皮尔逊系数值均大于0.8，这表明半滞回耗能试验值与估算值之间存在极强的相关性。

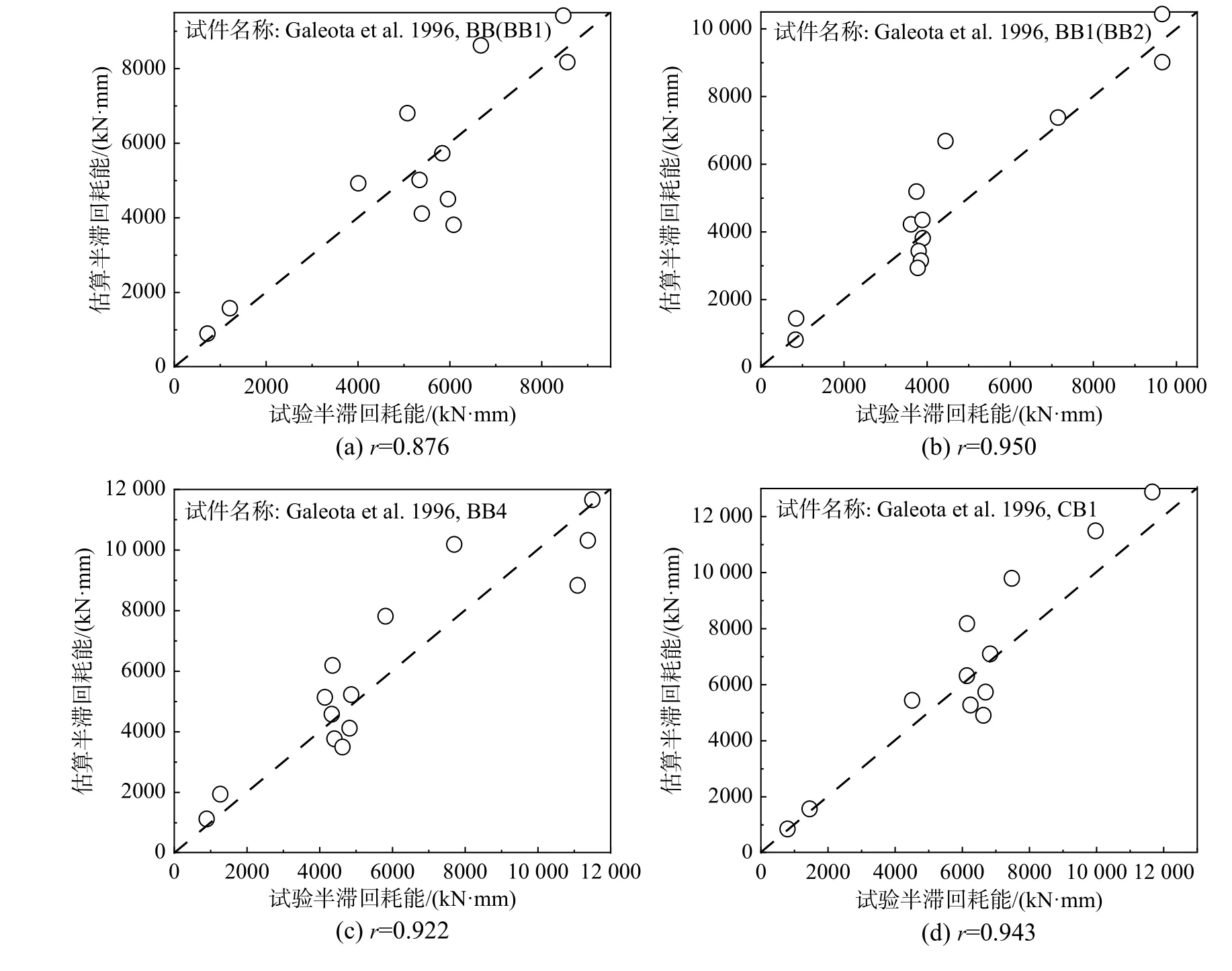
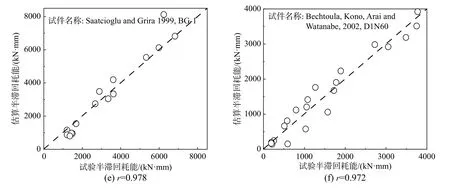
图13 6根试件半滞回耗能的分布Fig.13 Distribution of semi-hysteretic energy dissipation of six specimens

计算剩余试件半滞回耗能试验值和估算值的皮尔逊系数，结果为：相关性程度中等(0.4＜r≤0.6)的试件数目仅为2，其试件加载模式分别为稳态变幅加载和标准试验加载；相关性强(0.6＜r≤0.8)的试件数目为19，加载模式为稳态变幅加载的试件11个、标准试验加载3个、任意变幅加载5个；相关性极强(0.8＜r≤1.0)的试件数目为59，加载模式为稳态变幅加载的试件34个、标准试验加载13个、任意变幅加载12个且相关性极强的试件占总数73.75%，这表明耗能能力计算方法对样本空间中多数试件的计算结果偏优。且该方法对任意加载模式的RC构件耗能估算而言，具有较好的普遍适用性。

将80根试件累计耗能的计算结果放入以试验累积滞回耗能值为横坐标、估算累积滞回耗能值为纵坐标的坐标系中，如图14所示。

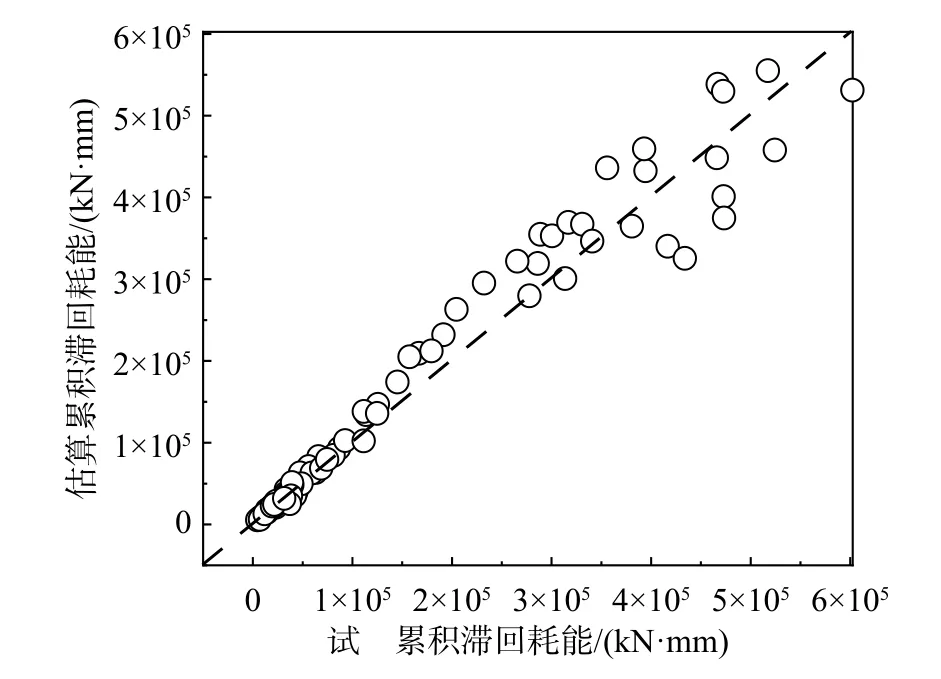
图14 80根试件累积滞回耗能的分布Fig.14 Distribution of cumulative hysteretic energy consumption of 80 specimens

同样的，图14虚线上的数据点表示其试件累积滞回耗能试验值与估算值相等。由图可知，其数据点均围绕该虚线分布，且累计耗能量在0～1×105范围内的数据点和虚线更为贴近(图15(a))，该范围内累计耗能试验值和估算值的皮尔逊系数为0.994，而累计耗能量在1×105～6×105范围内的数据点分布较为松散(图15(b))，皮尔逊系数为0.683，该现象可能与文献[20]中自主设计试件的累计耗能量有关：22根试件的总滞回耗能量均在1×105以下。由此可知，该计算方法对于累积滞回耗能量较小(＜1×105kN·mm)试件的计算结果要优于累积滞回耗能量较大(＞1×105kN·mm)的试件。

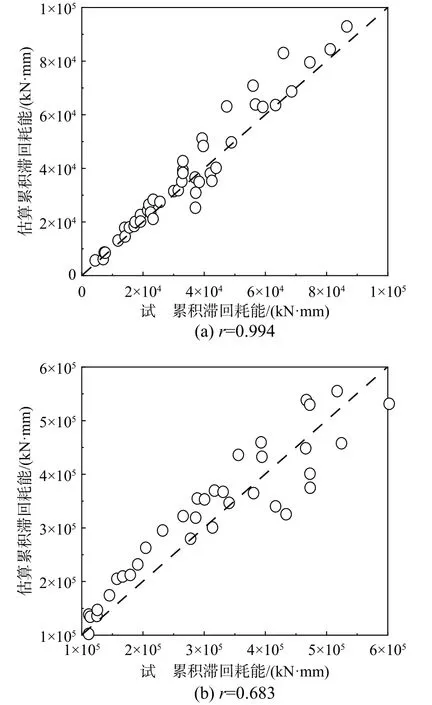
图15 根据累积滞回耗能量划分区间Fig.15 Divides zones according to accumulated hysteretic energy consumption

4 结论

本文利用文献[20]中18根稳态变幅加载RC构件，对其原始滞回数据进行处理及拟合分析，可以得到如下结论：

(1)稳态变幅加载方式下，RC构件后续任意滞回阶段D-n曲线走势决定于历史最大位移和已累积耗散的能量，即后续任意滞回阶段D-n曲线均可由以该滞回阶段为初始滞回阶段的D-n曲线平移得到。

(2)基于平移假设，通过拆分18根稳态变幅加载试件的D-n曲线进行拟合，提出了优化后的耗能能力计算方法。对于作为提出该方法理论支撑的22根RC构件，优化后的模型相较传统模型无论是过程估算还是结果估算上，均表现出更高的准确性及稳定性；对于从PEER数据库中选取的加载模式多样的80根试件，该方法表现出较好的普遍适用性，以及针对小耗能构件估算准确性更高的特点。

(3)为拓展所提出的耗能能力计算方法的适用性、可靠性以及应用的普及性，需针对轴向力、剪跨比、混凝土强度等设计参数以及累计滞回耗能量这一最终目标，设置科学、有效且充足的对照试验来分析对计算方法的影响。