基于大涡模拟的大气边界层湍流强度对低矮房屋风荷载特性影响研究

杨庆山，陈飞新，赵 乐,3，闫渤文

(1. 重庆大学土木工程学院，重庆 400045；2. 结构风工程与城市风环境北京市重点实验室，北京交通大学，北京 100044；3. 中机国际工程设计研究院有限责任公司，湖南，长沙 410000)

风灾是我国遭受的主要的自然灾害之一，据国家减灾中心统计[1]，仅2018年一年，风灾带来的直接经济损失就高达697.3亿元，占全国自然灾害总经济损失的26%。历次风灾调查表明，低矮房屋损毁所带来的损失占我国风灾损失的50%以上[2]。因此，深入理解和掌握低矮房屋的风荷载特性以及风压分布规律，从而提升和改进其抗风性能是十分必要的。

国内外学者对低矮房屋风荷载特性开展了系统的研究，主要方法有现场实测、风洞试验以及数值模拟。基于现场实测方法，国内外学者对低矮房屋的风荷载特性开展了大量系统的研究，考虑了不同类型的风场作用情况，包括季候风常规大气边界层风场[3−5]以及台风、飓风[6−7]等强风风场，为开展结构风效应研究提供了参考标准。其中，Levitan等[4−5]在美国德州理工大学(TTU)对一可转动的小坡度双坡屋面低矮房屋风荷载特性进行了长期实测，同时也测定了房屋周围的风场信息，积累了大量近地边界层风场特性以及低矮房屋屋面风压实测数据，现作为低矮房屋基准模型，被广泛用于低矮建筑缩尺风洞实验以及数值模拟研究。现场实测可以提供屋盖表面风荷载分布的真实数据，但其周期长，环境因素难以控制，无法开展系统参数化研究。

相比现场实测，风洞试验方法具有来流特性可控、周期短、可开展参数化研究等优势。围绕TTU低矮实验房标准模型，学者们开展了大量风洞实验研究。Ham等[8]对TTU标准模型进行了低湍流度下的1∶50缩尺风洞实验，通过对比实验与实测的屋面风压结果，验证了风洞实验方法的可靠性。聂少锋等[9]在TTU标准模型的基础上，对四坡屋面低矮房屋也进行了分析，并且同时考虑了多种因素的影响，明确了风向角、屋面坡度、屋面形式对屋面风荷载特征产生较大影响。Fritz等[10]、Bienkiewicz等[11]和Simiu[12]对比了在不同的风洞实验室得到的低矮房屋屋面风荷载特性，发现不同风洞中模拟的来流条件差异对于房屋表面的风压有显著影响，指明了来流特性准确模拟的重要性。戴益民等[13]考虑了不同地貌条件以及风向角，结果表明随着地面粗糙度增加，低矮房屋表面的平均、脉动、极小值风压系数逐渐增加。

随着高性能计算资源的飞速发展，计算流体力学(Computational fluid dynamics, CFD)数值模拟方法被逐渐运用到低矮房屋的风荷载特性研究中。相比于传统风洞试验，CFD数值模拟方法具有费用低、周期短、效率高的优点，并且可以获取全流域信息，以便对其机理进行更深入的分析。目前，湍流的数值模拟方法主要有雷诺平均方法(Reynolds-averaged navier-stokes，RANS)及大涡模拟方法(Large-eddy simulation, LES)。Bekele和Hangan[14]、顾明等[15]、周绪红等[16]采用RANS湍流模型对TTU模型周围流场进行了模拟，得到的建筑表面平均风压与实测结果吻合较好，且在此基础上考虑了屋面坡度、风向角因素的影响。然而，由于该方法是基于时均后的Navier-Stokes方程，得到的脉动压力与实测结果差别较大，并且无法反应瞬时流场信息。相比之下，LES方法在时间尺度上对湍流的非定常运动进行直接求解，只对大于网格尺度的湍流运动进行模拟，因而克服了RANS模型无法直接描述非定常流动特性的主要缺陷，不仅可以给出较好的平均风荷载信息，也可以给出比较接近实际的脉动荷载以及瞬时流场信息，但LES方法对网格精度、计算资源的要求相对较高。Selvam[17]基于TTU的现场实测和风洞实验结果，验证了LES能够模拟大气边界层下低矮房屋风压分布的特性。生成满足大气边界层风场特性的入口湍流是开展结构风效应LES研究的关键问题，目前主要有预前模拟法和人工合成法两类主要的LES入口湍流生成方法[18]。Nozawa[19]等在对TTU模型的LES研究中，采用了预前模拟方法获得入口湍流，在计算域前部预前模拟粗糙元以考虑不同地貌情况，较好的预测了不同地貌情况下的屋面风压统计量的变化规律，但是这种通过预前模拟获得入口湍流的方式无法直接定义目标湍流特性(湍流度、湍流积分尺度和风速谱等)，并且计算成本极高。人工合成法基本思想是基于严格的数理推导，在入口平面构造满足目标湍流特性和空间相关性的风速时程序列作为入口边界条件，且计算效率相对较高。Kraichnan等[20]首先采用人工合成方法生成了均匀各向同性的脉动风场。Smirnov等[21]在Kraichnan等[20]的算法基础上提出了RFG(Random flow generation)方法，引入了湍流长度尺度和时间尺度，并且通过比例和正交变换生成了非均匀各向异性、满足高斯谱的脉动风场。周晅毅等[22]将 RFG方法用于了TTU模型表面风压的的大涡模拟研究，其平均风压、脉动风压及风压相干性与风洞实验及现场实测结果具有良好的一致性，但是实际中大气边界层湍流风速谱无法满足高斯谱的假定，导致RFG方法在风工程研究中不具普适性。Huang等[23]提出了能够模拟任意功率谱形式的脉动风场的DSRFG(Discretizing and synthesizing random flow generation)方法，该方法生成的脉动速度满足连续性方程，并且适用于并行计算。Castro等[24]在DSRFG方法的基础上通过引入时间尺度参数考虑了脉动风速时程序列的时间相关性。Aboshosha等[25]提出了CDRFG(Consistent discretizing random flow generation)方法，在DSRFG方法的基础上修正了脉动风速功率谱在频率上的分布，通过建立湍流积分尺度与频率间的关系生成了满足空间相关性的脉动风场。周桐等[26]通过对比研究发现，CDRFG方法合成的大气边界层湍流的平均风剖面与湍流度剖面与目标值均能较好吻合，仅湍流度在计算域下游的近地面处由于壁面效应而有细微差异，且在保证合理的网格分辨率情况下，入口湍流在计算域内具有较好的自保持性。综上，现有研究表明：低矮屋盖表面的风压特性主要会受到屋面外形、来流湍流以及风向角几个方面因素的影响，其中对于外形、风向角因素的影响已经进行了较为系统的研究，但对于来流湍流影响的研究相对较少，且主要存在以下不足之处：其一，对来流特性考虑不足，只考虑了不同的地貌情况来流的影响，在改变边界层来流湍流度的同时，平均风速以及剖面指数均发生较大的改变，没有做到控制单一变量进行精细化的湍流参数分析，因此，目前尚缺乏关于大气边界层湍流度对低矮屋盖风荷载影响的研究；其二，在已有的模拟研究中采用的人工合成湍流方法生成的湍流自保持性无法保证，且对于湍流度对于极小值风压的影响的研究较少，以及缺乏对风压脉动变化规律与湍流流场特征之间的相关性的机理分析。

因此，本文基于LES方法，结合TTU标准模型的实测以及缩尺风洞实验数据，对TTU模型的风荷载特征进行了模拟分析。采用CDRFG人工合成湍流方法生成边界层湍流，在验证了来流湍流自保持性的基础上，以湍流度为单一变量，同时保证边界层来流的风速剖面一致，研究了来流湍流度对低矮建筑表面的平均、脉动以及极小值风压分布以及风压非高斯特性的影响，并且从湍流流场的角度进行了机理阐释。

1 TTU现场实测与风洞试验

本文的数值模拟工作参照了TTU标准模型的实测风压结果[4−5]，以及科罗拉多州立大学(Colorado state university, CSU)完成的TTU模型的缩尺风洞测压实验结果[8]。现场实测实验房的尺寸为13.7 m(长)×9.1 m(宽)×4.0 m(高)，坡度小于10%。缩尺模型风洞试验的几何缩尺比为1∶50，风速缩尺比为1∶1，时间缩尺比为1∶50，缩尺后模型尺寸为：0.276 m(L)×0.184 m(B)×0.080 m(H)。风洞实验中的房屋表面风压测点布置情况与现场实测基本一致，TTU模型及测压点布置如图1所示。

图1 TTU模型示意图及测压点布置[3−5]Fig. 1 TTU building model and pressure tap arrangement[3−5]

2 数值模拟方法

2.1 大涡模拟

大涡模拟是由Smagorinsky[27]提出的湍流模拟方法，其基本思想是同通过制定空间滤波函数将湍流分解为可解尺度湍流脉动和不可解尺度湍流脉动，对可解尺度湍流脉动进行直接数值模拟，对不可解尺度湍流脉动采用亚格子模型来描述。空间滤波后的不可压缩流动大涡模拟控制方程为：

式中：xi和xj为流动区域中的空间坐标，下标 i和j分别为笛卡尔坐标系中的不同方向，包括顺风向、横风向以及竖向；t 为时间；u¯、p¯分别为滤波后的速度和压力；ρ 、μ分别为空气密度和粘度；τij为亚格子应力。为使控制方程封闭，需建立亚格子(Sub-grid scale, SGS)模型。本文采用标准Smagorinsky亚格子模型，其亚格子应力形式为：

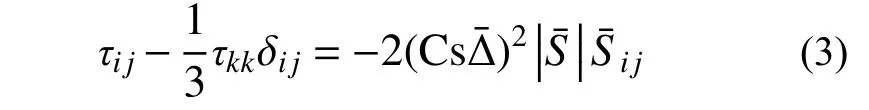
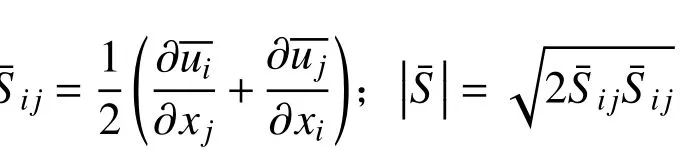
2.2 计算域及网格划分

数值模拟计算域尺寸为15 L(长)×5 B(宽)×6 H(高)，模型位于参考坐标系的中心处，模型尺寸与参考实验的缩尺模型保持一致，计算域以及模型如图2所示，其中，建筑模型距离入口和出口的距离分别为5 L和10 L，考虑了0°(正风向)和45°(斜风向)两个风向情况，数值模拟中模型阻塞率约为3.3%＜5%，满足计算风工程研究的要求。

图2 计算域尺寸及建筑模型位置Fig. 2 Computational domain and location of TTU model

0°风向角下的模型网格划分情况如图3所示，采用结构化网格进行划分，对建筑周围的近壁区网格进行了加密处理，具体的加密方式为：靠近建筑物壁面的首层网格高度为2×10−4m (y+＜5)，近壁区网格增长率不超过1.05，近壁区包括离模型迎风面、顶面、两侧面1.0 H以及模型背风面2.0 H内的区域；远离建筑模型位置采用相对稀疏的网格布置，其网格增长率不超过1.1；45°风向角下的网格划分策略与0°风向角类似。

图3 数值模型网格划分Fig. 3 Grid meshing arrangement of the computational domain

为了验证网格无关性，以0°风向角的网格为基础，GCI(Grid convergence index)方法进行网格无关性验证[28]，通过选取计算得的迎风面屋面前缘分离处的风压结果作为参考量，对比其在不同网格疏密程度情况下计算得到的误差以量化因网格疏密变化所造成的结果误差。本文考虑了三套不同疏密程度的网格，即稀疏网格(coarse)、基础网格(basis)以及加密网格(refined)，不同网格的疏密差别主要体现在近壁区网格尺寸与数量上，如图4所示。

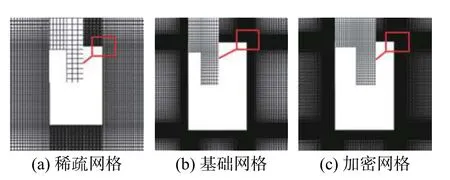
图4 不同网格划分策略Fig. 4 Different grid meshing strategies

网格无关性分析结果见表1，其中，下标1、2、3依次代表加密网格、基础网格、稀疏网格。通过观察GCI指数可以发现，不同网格之间的模拟结果存在差异，且随着网格量的增加，不同网格计算结果之间的误差会逐渐缩小。其中，基础网格计算结果与加密网格计算结果之间的相对误差在3%以内，满足计算精度要求，因而本文选择基础网格进行后续的研究。

表1 网格无关性分析Table1 Grid-independent results

2.3 边界条件

本文的计算域入口采用速度入口边界，其输入参数为基于CDRFG方法生成的满足目标风场特性的脉动风速时程；出口采用顺流向的速度、压力梯度均为0的流动出口(outflow)边界；计算域侧面及顶面边界采用了对称(symmetry)边界，其物理意义为假定该边界上的法向速度分量以及所有速度分量的法向梯度均为0，减小了侧边以及顶边的边界效应对房屋模型风效应的影响；房屋表面以及地面采用了无滑移壁面边界条件，其所有速度分量及法向压力梯度均为0，由于标准Smagorinsky亚格子模型无法较好地模拟近壁面处的湍流行为，本文采用了Werner-Wengle壁面函数进行修正，对房屋表面及地面近壁区的风速信息分布采用指数律函数作为壁面剪切应力的近似解，表达如下：

式中：μp为壁面平行速度；A、B为常数，分别取8.3和1/7；Δz为近壁面控制体特征尺度。该壁面函数根据不同的壁面y+值选定不同的壁面处理方式，具有较好的网格适应性，被广泛应用于风工程数值模拟研究中[29−31]。

2.4 入口湍流生成及其自保持性验证

本研究采用CDRFG方法，基于通用流体力学软件ANSYS Fluent 19.2，通过自编的入口UDF(User defined function) 实现生成与参考实验一致的来流，为了确保合成湍流的准确性及其自保持性，建立了空风场数值模型进行计算。空风场计算域尺寸与有建筑的风场尺寸一致，并且空风场的网格划分疏密程度与基础网格基本一致，尤其是模型上游位置的网格，空风场网格总数为610万，如图5所示。

图5 空风场网格划分Fig. 5 Grid meshing arrangement of empty computational domain

在空风场中计算得出的湍流来流的自保持性验证结果如图6所示，其中： Uref为参考高度处(房屋屋檐高度处)的风速；为参考高度处风速方差；Lu为顺风向积分尺度。

生成的边界层来流平均风剖面和湍流度剖面与实验结果吻合较好，且在计算域入口处与模型位置处的平均风剖面和湍流度剖面基本一致，剖面的自保持性较好；来流的参考高度处无量纲风速谱结果中，横坐标为无量纲频率 nL/Uref。图6中结果表明：风速功率谱密度在折减频率高于1.0处衰减较为明显，即来流截断频率为1.0左右，这是由于顺风向网格的过滤效应导致的。考虑到对低矮房屋的结构特征频率远低于来流截断频率1.0，且在低于1.0的频率成分处风速功率谱整体自保持性较好，说明合成的入口来流是准确有效且满足自保持性的。

图6 来流湍流自保持性Fig. 6 Self-sustainability of upstream turbulence

2.5 工况设定

控制湍流度为单一变量，共生成了四种不同的边界层湍流工况，本文将四种来流工况按照湍流度由小到大分别命名为TI1、TI2、 TI3、TI4，如图7所示，其中TI3为与实验一致的来流条件。

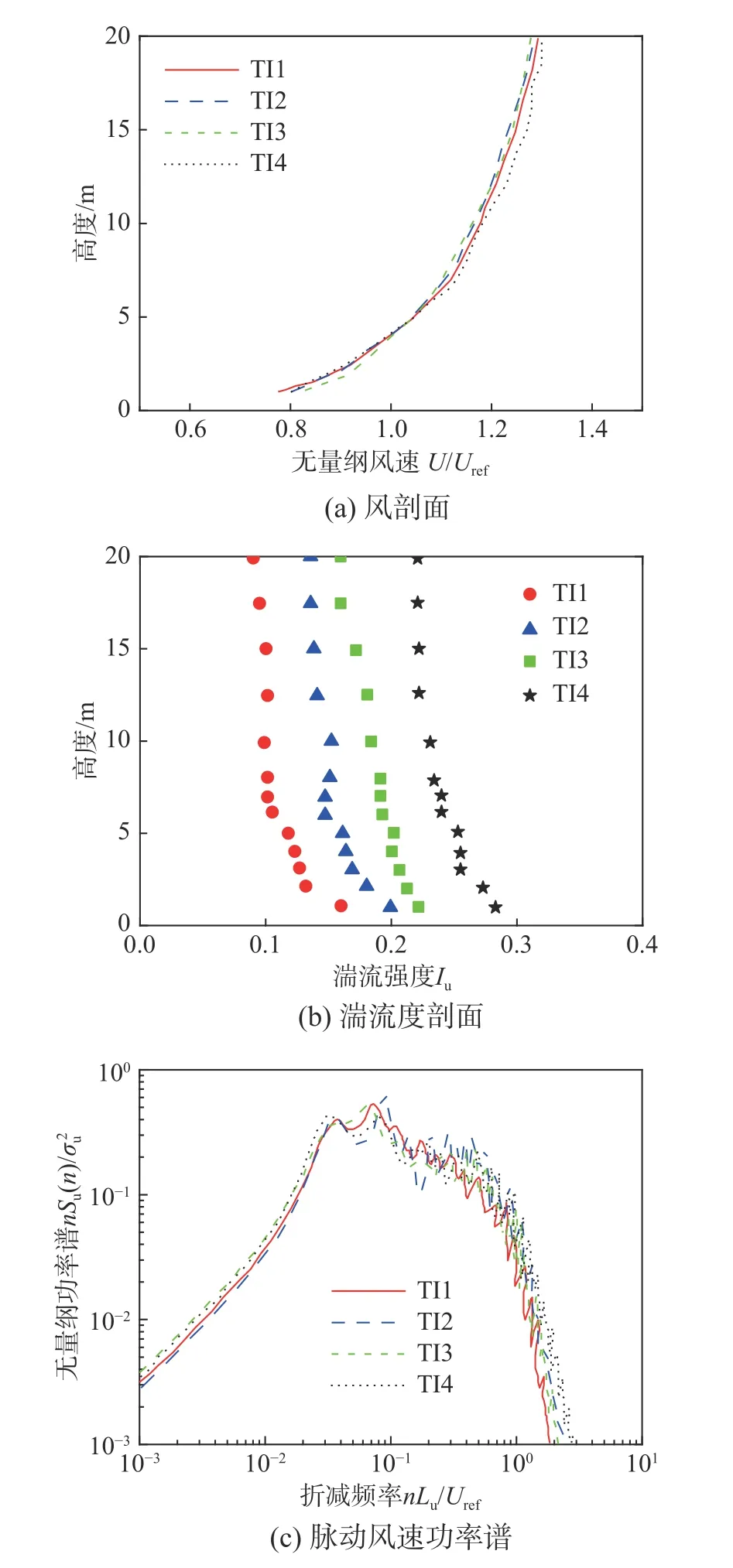
图7 四种不同湍流工况Fig. 7 Four scenarios of upstream turbulence conditions with different turbulence intensity

四种湍流工况在参考高度处(屋檐高度处)的流场参数如表2所示，其中：α为地面粗糙度类别；Iu、Iv、Iw分别为顺风向、横风向和竖向的湍流度； Lux为顺流向的湍流积分尺度。除了湍流度，保证了各种来流情况的风速以及湍流剖面基本一致。

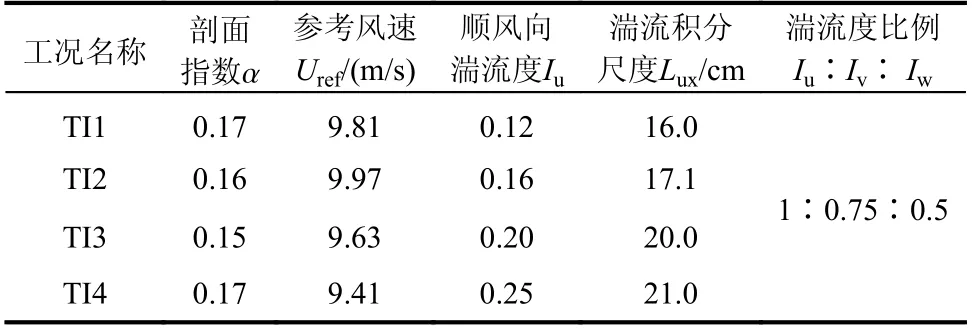
表2 参考高度处的流场参数Table2 Flow parameters at reference height

2.6 求解策略以及测点布置

本文数值模拟工作依托广州超算中心完成，采用超线程24核Xeon E5 CPU进行计算，基于通用计算流体力学仿真平台ANSYS Fluent 19.2对滤波后的N-S方程进行求解。有建筑模型的风场与空风场的求解策略完全一致，其中时间和空间离散均采用二阶离散格式，时间项采用二阶隐式离散格式，空间项采用有界中心差分格式，压力梯度项采用least-square cell-based格式，扩散项离散采用二阶中心差分格式，对流空间离散采用二阶中心差分格式，其二阶精度保证了数值模拟的准确性。对于离散方程组的求解采用SIMPLE(Semiimplicit method for pressure-linked equations)算法。进行大涡模拟计算前，先采用RNG k-ε湍流模型对流场进行定常模拟，即将RANS模拟得到的定常流场结果瞬态化后作为大涡模拟的初始条件，从而加速LES模拟中的湍流流场发展并提高收敛速度。

为满足库朗数CFL＜1的要求，无量纲时间步长ΔtUH/H取为0.0132。为了得到稳定的收敛解，以风按参考风速流经整个流域的时间为参考时间，称为全流域时间(Flow-through time)。初步试算经过6个全流域时间后监测点的风速基本稳定，用第7个～第30个全流域时间内的模拟结果可以获得平稳的统计值。因此，对每个工况均计算30个全流域时间，且取第7个～第30个全流域时间内的计算结果进行分析，对应的无量纲时长tUH/H约为1200。

图8 屋面风压测点布置Fig. 8 Pressure taps distribution on the model roof

分析得到的无量纲风压系数如下：

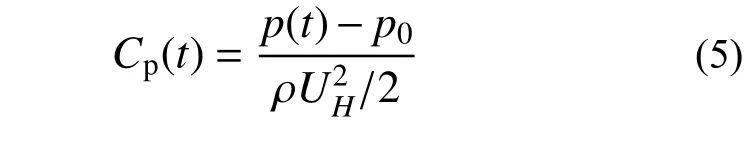
式中： p(t) 为建筑表面风压；p0为参考静压；UH为屋檐高度处的风速。风压系数的平均值，标准差，以及极小值分别为平均风压系数，脉动风压系数，以及极小值风压系数。

3 结果与讨论

3.1 数值模拟验证

图9给出了TI3条件下，0°及45°风向角下房屋中轴线上的模拟、参考实验以及实测的风压系数统计量结果对比，包括平均风压系数、脉动风压系数以及极小值风压系数，并给出了TTU实测风压系数结果的误差棒，以考虑实测风压系数结果的不确定度。其中，BC段为屋面中轴线，AB、CD段分别为迎风面与背风面中轴线。

由图9可见，屋面上较强的平均负压主要出现在屋面迎风前缘部分，同时该处的脉动风压系数达到最大，极小值风压系数达到最小。0°以及45°风向角下大涡模拟与实验以及实测的平均、脉动、极小值风压系数结果总体分布规律上吻合较好；平均风压系数结果均位于实测数据误差线以内且与实验结果也基本吻合；极小值风压系数模拟结果基本位于实测数据误差线以内，只有迎风前缘极少区域极小值风压系数在实测误差线以外，误差小于10%；屋面后缘及背风面上局部区域的脉动风压系数模拟结果相比实验与实测结果偏大，主要在0°风向角下，且误差小于20%。误差原因是人工合成湍流的高频脉动成分偏小，无法完全再现实验以及实测中的来流脉动成分，但考虑到风压系数结构的趋势基本与实验以及实测结果一致，且脉动风压系数误差量级以及误差区域都较小，可认为本文模拟是准确有效的，可用于后续分析。

图9 风压系数统计量模拟结果与参考试验对比Fig. 9 Validation of the statistics of wind pressure coefficients

3.2 来流湍流度对屋面风压的影响

3.2.1 屋面风压统计量特性

图10～图11分别展示了TI1和TI3两种来流条件下，屋面分别在0°和45°风向角下的平均、脉动以及极小值风压系数云图。

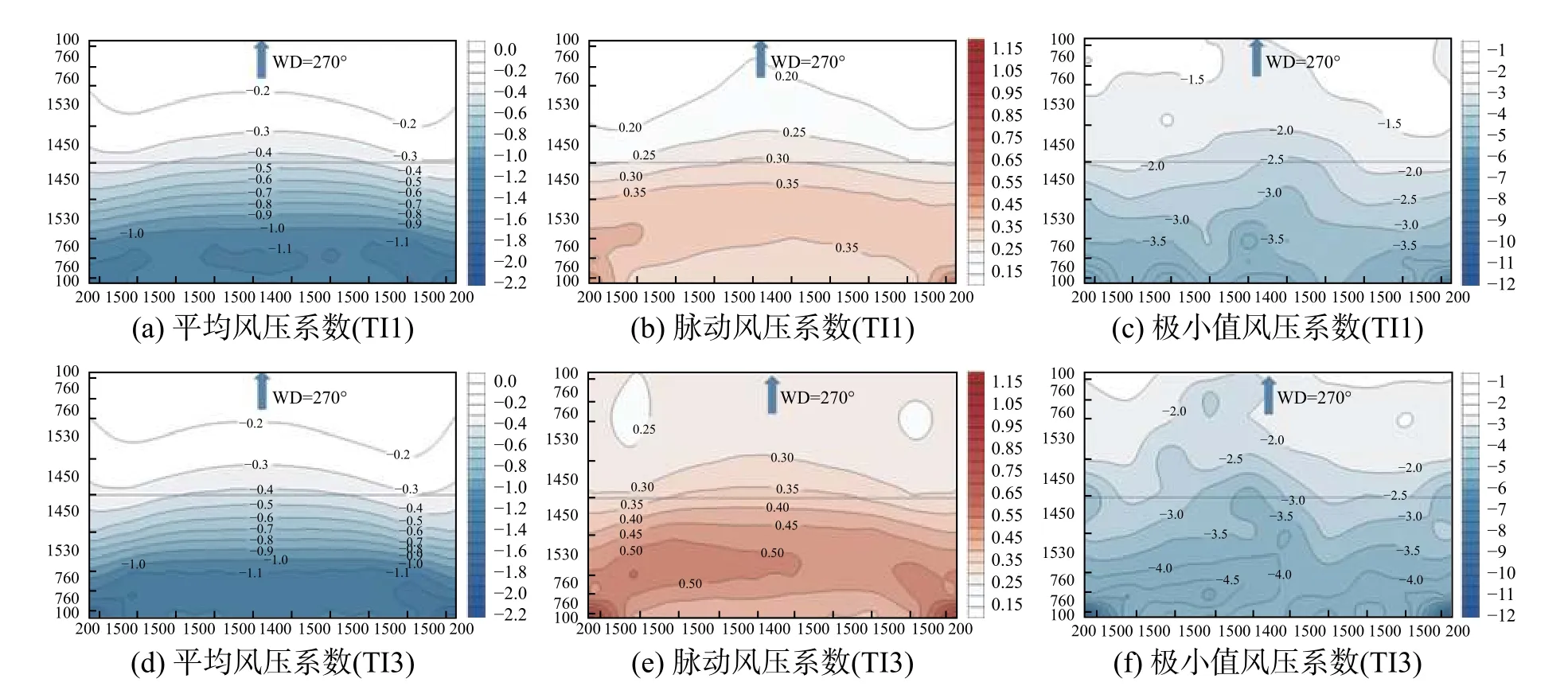
图10 0°风向角TI1和TI3两种来流下的风压统计量Fig. 10 Statistics of wind pressure coefficients under TI1 and TI3 in the wind direction of 0°

0°风向角情况下，屋面风压分布关于中轴线对称，由于气流在建筑屋面前缘发生较强的流动分离形成柱状涡，迎风前缘处出现较大的负压区，其中平均、极小值风压系数达到最小，脉动风压系数达到最大，其中平均风压系数最小的位置连线可视为柱状涡的中心线，脉动风压系数最大的位置可视为柱状涡再附点[32]。两种不同湍流度条件下，平均风压系数结果受湍流度影响较小，湍流度主要影响脉动以及极小值风压系数幅值，随着湍流度由12%增大至20%，屋面的脉动风压系数整体增大，极小值风压系数整体减小，但风压整体分布趋势基本一致。其中柱状涡内的脉动风压系数最大值由0.35增大至0.51，极小值风压系数由−3.5减小至−4.5。

A：其实我现在过的生活就是我理想中的样子，做自己喜欢的事情，家人健康平安。未来希望能找到和自己志趣相投的另一半，相互陪伴依靠并且组建家庭，生个孩子养只宠物，依然做着自己喜欢的事情，用心感受生活感受快乐，这样的生活就足够了。

45°风向角情况下，屋面风压分布关于屋面对角线大致对称，由于气流在建筑屋面的两个迎风屋檐均发生了流动分离形成锥形涡，两个迎风侧边前缘处均呈钟形分布的较强负压区，图11中给出了负压区内平均风压系数最小值的连线，可认为是锥形涡的中心[33]，称为涡迹线。随着湍流度由12%增大至20%，屋盖表面负的平均风压系数大小仍然基本保持不变，脉动风压系数整体增大，极小值风压系数整体减小，两个锥形涡内的脉动风压系数最大值由0.35增大至0.55，极小值风压系数由−2.5减小至−3.5。同时，屋面锥形涡迹线与迎风前缘的夹角α也明显随着湍流度的增大而减小，由14.4°减小至10.7°。

为了便于更明确的分析湍流度对平均、脉动、极小值风压系数的影响，图12给出了四种不同来流条件下房屋中轴线上的平均、脉动、极小值风压系数分布结果，考虑了0°和45°两种风向角情况。

图12 四种不同湍流情况下中轴线风压系数统计量Fig. 12 Statistics of wind pressure coefficients under four different turbulence conditions

结果表明：0°风向角时，平均风压系数随湍流度的变化整体上变化较小，但在屋盖前缘1 m～2 m处的分离区，最小平均风压系数的位置随着湍流度的增大而向前移动，表明柱状涡的中心线逐渐向迎风前缘移动，柱状涡的形成逐渐被抑制；脉动风压系数随着湍流度的增大而呈现线性增大的趋势，特别是在屋面及尾流区其脉动风压系数受湍流的影响比较显著，最大脉动风压系数的位置随着湍流度的增大而向屋面前缘移动，表明柱状涡的再附位置也向迎风前缘移动；极小值风压同样受湍流度的影响较为明显，房屋表面的极小值风压系数绝对值随着湍流度的增大而减小，但其变化趋势相对脉动风压的变化趋势较小。45°风向角时，平均风压系数随湍流度的变化趋势与0°风向角的趋势基本一致；脉动和极小值风压系数随湍流度的增加而线性变化趋势相比0°风向角情况更加明显，并且当湍流度增大至25%，屋面脉动、极小值风压系数(尤其是屋面后半部分)增加、减小的趋势愈加剧烈，呈现非线性变化的趋势。另外，从图13给出的不同湍流度下锥形涡涡迹线与迎风前缘的夹角α的结果来看，α随着湍流度的增加而线性下降，即锥形涡的形成由于湍流度的增加而受到明显抑制。

图13 涡迹线与屋缘夹角变化规律Fig. 13 Angles between the vortex trace and the roof edge

3.2.2 屋面风压非高斯特性

图14分别给出了TI3来流条件下，在0°和45°风向角下的屋面风压偏度(skewness)与峰度(kurtosis)云图结果。其中，偏度和峰度分别为风压脉动时程的三阶矩和四阶矩，用于描述风压非高斯随机过程[34]。

如图14所示，0°风向角下，在建筑物迎风屋面前缘角部、屋脊两边等流动分离强烈的柱状涡区域，风压呈现明显的非高斯特性，以软化右偏非高斯过程( α3＜0,α4＞3)为主，并且在屋脊附近区域，风压也表现出右偏软化非高斯特征，主要是由涡再附以及由屋脊线的存在而造成的流动分离导致。在45°风向角情况下，屋面迎风角部以及沿锥形涡分布的区域呈现较强的非高斯特性，且在靠近迎风长边一侧的锥形涡区域非高斯特性更强，偏度最大达到了−1.0，峰度最大达到了7.0，显然，此时将屋面角部区域的风压作为高斯过程是偏不安全。由0°和45°的结果来看，屋面风压的非高斯特性较强的区域主要出现在屋面由于流体分离而形成的柱状涡、锥形涡的区域内，即风压非高斯特性主要是由于屋盖表面的涡的存在导致的。

图14 TI3下不同风向角下屋面风压的偏度与峰度Fig. 14 Skewness and kurtosis of wind pressure coefficients under TI3

45°风向角情况下屋面风压的非高斯特性要明显强于0°，为了分析湍流度对于屋面非高斯特征的影响，仅针对45°风向角情况展开分析，图15给出了TI2、TI4两种不同湍流度来流情况下的屋面风压的偏度、峰度系数云图结果。

图15 TI2和TI4来流下屋面风压的偏度与峰度Fig. 15 Skewness and kurtosis of wind pressure coefficients under TI2 and TI4

结果表明：从分布区域上看，不同湍流度情况下，屋面表面风压表现出较强非高斯特性的区域基本一致，均为迎风角部以及沿锥形涡分布的区域，且随着湍流度的增加，屋面风压非高斯区域的面积逐渐减小，且出现由多个非高斯较强的中心区域沿锥形涡分布逐渐变为迎风前缘的一个非高斯中心区域主导的趋势；从偏度、峰度数值上看，各种来流下均表现出右偏软化非高斯特征；在湍流度相对较小的情况下，屋面风压非高斯特性较为强烈，在迎风角部区域，偏度最小达到了−1.5，峰度最大达到了8.0；随着湍流度的增加，负的偏度系数逐渐增大，峰度系数逐渐减小，即风压非高斯特性逐渐减弱，在湍流度增加至25%时，偏度系数最小为−1.0，峰度系数最大仅为5.0。

为了进一步分析屋盖表面风压的非高斯特性，仍然针对45°风向角情况，取屋面非高斯特性表现较强的区域沿屋面对角线上的G1、G2、G3、G4四个典型测点，图16给出了四个典型测点在四种不同湍流来流情况下的风压概率密度曲线结果，并且给出了高斯分布曲线作为对比。

图16 不同来流湍流下典型测点风压系数概率密度函数Fig. 16 PDF of pressure characteristics at typical pressure taps under four different upstream turbulence conditions

结果表明：四个典型测点风压概率密度曲线在四种不同湍流强度情况下均呈现明显的软化非高斯特征，且均随着湍流强度的增强而软化特征逐渐减弱。其中，处在迎风屋角处的G1测点的风压概率密度曲线右偏非高斯特征也非常明显，并且随着湍流强度的增加其软化特征减弱而右偏特征程度逐渐增加，且在低湍流时出现双峰的特征；靠近迎风屋角的G2测点的风压概率密度曲线非高斯特性在四个典型测点中最为明显，且在湍流度增加至25%时呈现双峰特征；靠近背风屋角G3、G4处的风压概率密度曲线规律接近，主要表现出风压软化非高斯特征随着湍流强度的增加而减弱的趋势。

3.3 流场机理解释

本文基于Q准则[35]对带挑檐双坡屋面低矮房屋表面的流场结构进行识别。Q为速度梯度张量的二次不变量，其定义为 Q=(ΩijΩij−SijSij)/2，和Sij=(μi,j+μj,i)/2 。当 Q＞0时，相比流体的应变率 (SijSij) ，转动速率 (ΩijΩij)占主导，即流场中涡旋结构占主导地位。图17给出了四种不同湍流来流情况下45°风向角时建筑物表面的涡结构图(其中 Q=6.0×105s−2)，并采用压力系数对其进行着色，以分析不同湍流度情况下低矮房屋模型表面的流场结构及其与风压分布特性的之间的关系机理。

结果表明：在边界层湍流来流作用下，屋面两个迎风前缘处均出现了明显的锥形涡结构，其由迎风屋角开始分别沿着两个迎风边呈锥形分布，同时由于逆压梯度的作用，锥形涡内形成较强的负压区，并且在屋面周围远离迎风边的位置均由于锥形涡的移动出现了较多的不同尺度的涡，锥形涡迹线的位置也在图17中给出，其与图11中由最大平均风压的位置判断出的涡迹线的位置是一致的。在TI1中，湍流度为12%，相对较低，此时屋面的锥形涡的直径较大且相对规则，且有明显的锥形涡结构，随着涡的的移动，屋面上方流场涡结构以大涡为主；随着湍流度逐渐增大至25%，涡迹线与迎风前缘的夹角以及锥形涡的直接均逐渐减小，同时迎风前缘的锥形涡结构逐渐变得不规则，尤其是TI4情况下的靠近迎风短边的涡结构；另外，随着来流湍流度的增加，屋面周围由于锥形涡的移动产生的涡的尺寸逐渐减小，小尺度涡成分逐渐增加且占主导。

结合上述流场结构结果以及3.2节风压分析结果，对屋面风压特征受湍流度影响的机理可进行如下解释：随着来流湍流度的增加，涡的形成被抑制，涡的直径减小，导致平均风压最小值、脉动风压最大值位置均前移；分离涡的规则性逐渐减弱，分离涡内部的涡结构逐渐被来流湍流打乱，涡内部的结构逐渐由大涡占主导变为小尺度涡占主导，因此流场脉动特性增加，导致屋面脉动风压增大、极小值风压减小；同时，由柱涡以及锥形涡造成的屋面风压非高斯特性也因此逐渐减弱。

4 结论

本文基于已有的TTU标准模型现场实测以及风洞实验数据，采用CFD数值模拟方法对不同来流湍流度下的低矮房屋风荷载特征变化规律进行了研究，主要结论如下：

(1)在来流湍流度由12%增大至25%的过程中，房屋表面的平均风压系数结果变化较小；脉动风压系数呈线性增大趋势；极小值风压系数变化规律相对复杂，呈现出非线性减小的趋势，最小可达−5.0；屋面涡脱逐渐被抑制，脉动风压与平均风压最大值出现的位置均前移，锥形涡涡迹线与迎风前缘的夹角由14.4°呈线性下降至8.7°。

(2)屋面风压的非高斯特性出现主要与屋面涡结构形成相关，以右偏软化非高斯过程为主，且随着湍流度的增加，风压非高斯特性逐渐减弱，并且在迎风屋角区域的风压概率密度函数会呈现双峰分布特征。

(3)随来流湍流度增加，分离涡的形成被抑制，分离泡直径减小，导致平均风压最小值、脉动风压的最大值位置均前移；分离涡规则性逐渐减弱，内部涡结构逐渐被来流湍流打乱，逐渐由大涡占主导变为小涡占主导，因此流场脉动特性增加，导致屋面脉动风压增加、极小值风压减小；同时，由柱涡以及锥形涡造成的屋面风压非高斯特性也因此逐渐减弱。