基于相空间重构改进算法的混沌奇异谱分析及应用

张立国， 刘 婉， 张淑清， 刘海涛， 董 伟， 宋姗姗

(燕山大学电气工程学院，河北秦皇岛066004)

1 引 言

奇异谱通过把时间序列信号向嵌入维数主轴分解，分解的每一个主成分代表着信号的特征成分[1]。信号主成分的大小分布反映出信号能量在对应嵌入维数主轴上的大小分布情况，主成分各个状态变量反映在整个系统中所占能量的相对关系[2]。因此，奇异谱技术不仅可以对动力系统的时间序列进行降噪，还可以作为动力系统特征提取的有效方法[3]。混沌奇异谱通过相空间重构，得到各主分量的图像谱值分布，从而提取混沌信号的特征信息。

相空间重构作为混沌时间序列处理中的重要课题，其最佳嵌入维数m和延迟时间τ的选取至关重要。如果m取值过小，吸引子会发生折叠甚至在某些地方会出现自相交，重构吸引子的几何形状和原始状态吸引子可能完全不同；如果m取值过大，当维数m大于最小嵌入维数的时候，几何结构已经被完全打开，此时这些几何不变量与嵌入的维数无关；如果τ取值太小，那么在相空间中各向量的分量间几乎不包括新信息，从而低估关联维数。相反，τ取值太大，相空间重构的相关有效信息会遗漏，这样会高估关联维数[4]。

m的确定方法很多，如饱和关联维数法、邻近点维数法、虚假邻近点法[5]。这些方法确定最佳嵌入维的原理大致相同，都是依据随嵌入维数m升高而逐步收敛的情况，但是没有给出如何确定m最终值的依据。

本文提出基于改进Cao算法[6]对m和τ的求取改进方法，解决了常用求取方法中所存在的计算方法复杂、计算量庞大、计算结果不精确等问题，并且可以快速有效地提取混沌动力系统中有用定量信息，重构系统的相空间。通过对Lorenz典型混沌系统进行数值仿真试验，结果表明，这两种方法结合能够有效地重构原系统的相空间。

在求取m和τ基础上，对混沌奇异谱特征量化特征进行分析，通过实验验证奇异谱分析技术不仅具有很强的稳定性以及抗噪性能，还能对不同信号进行明显区分。

本文方法在滚动轴承早期故障识别中应用，首先通过最大Lyapunov指数[7,8]判别机械故障数据具有混沌特性；然后，利用本文改进的混沌相空间重构方法得到最佳延迟时间和嵌入维数；最后得到混沌奇异谱，通过混沌奇异谱提取故障特征，将不同故障识别出来。为机械故障早期诊断提供一种新的有效途径。

2 基于CAO算法的混沌相空间重构

设x1,x2,…,xN是一个时间序列，并且其重构相空间向量[9]：

Ym(i)=[x(i),x(i+τ),…,x(i+(m-1)τ)]
i=1,2,…,N-(m-1)τ

(1)

(2)

定义：

(3)

(4)

E(m)仅取决于嵌入维数m和延迟时间τ，为了研究E(m)从m到m+1的变化，定义

E1(m)=E(m+1)/E(m)

(5)

从而发现当m大于某个值m0时，E1(m)停止变化。如果吸引子可以从m维相空间重构中获得，那么m0就是寻找的最小嵌入维数。

在进行E*(m)数值验证之前，需要定义另一个用于区分确定性信号和随机信号E2(m)的量：

(6)

E2(m)=E*(m+1)/E*(m)

(7)

3 改进的Cao算法

3.1 Cao算法存在的问题

当该时间序列为一串随机数字时，随着m的增加，E1(m)永远不会达到饱和值。但是在实际计算中，当m足够大时，很难去判断E1(m)缓慢增加还是停止改变。事实上，由于可观测的数据样本是有限的，即使时间序列是随机的，也有可能E1(m)在某个维度是停止变化的。

为了解决这个问题，增加了E2(m)这个参考量。对于随机数据，未来值对于过去值是无关的，因此，这种情况下，对于任何嵌入维数，E2(m)将趋近于1。然而，对于确定的时间序列，E2(m)是与m有关的，即对于所有的m，E2(m)不可能为某一定值。那么在不同的嵌入维数下，必存在一些E2(m)≠1的值。E1(m)用于计算确定时间序列的最小嵌入维数，E2(m)则是在实际应用中判断有序数列是在缓慢变化还是已经趋向于稳定。E1(m)和E2(m)的值在m大于某一特定值m0时停止变化。m0即为最佳嵌入维数。

3.2 确定嵌入维数的改进方法

嵌入维数m的确定是依据E1(m)停止变化为标准的，这个标准并没有给出判断停止变化的准则，只是依靠主观判断，实际上，时间序列E1(m)经常是有起伏的，很少出现严格意义上的停止变化，所以，这给m的确定带来了困难。

针对这一问题，本文利用补充准则E2(m)进行联合判断，同时对CAO算法提出了改进，给出了一种改进的嵌入维数的稳定性准则[10]，计算步骤如下：

1) 计算Δi：

Δi=|E1(i)-E1(i+1)|, 1≤i≤N-1

(8)

式中：|E1(i)-E1(i+1)|表示计算E1(i)与E1(i+1)的差值的绝对值，结果用Δi来表示。

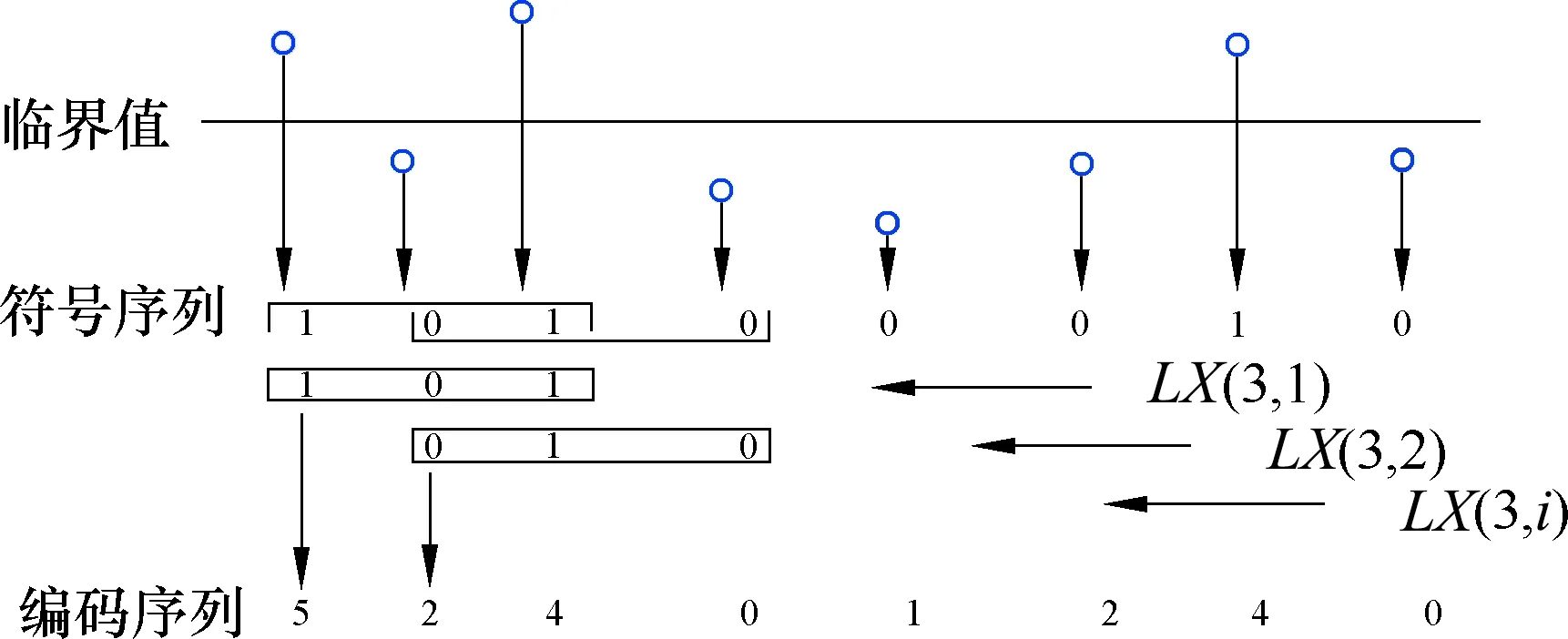
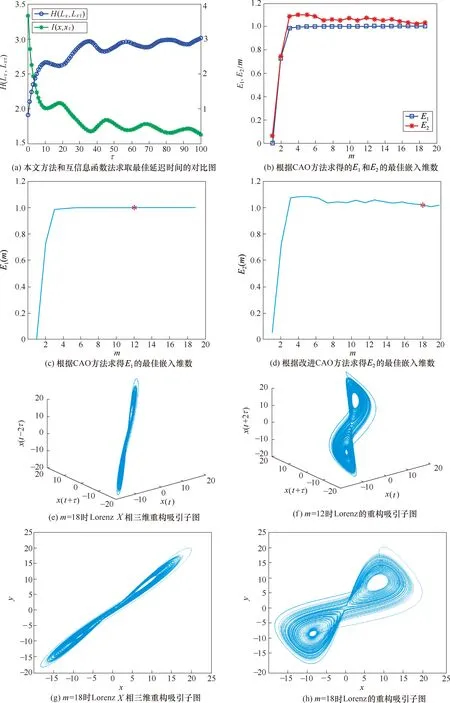
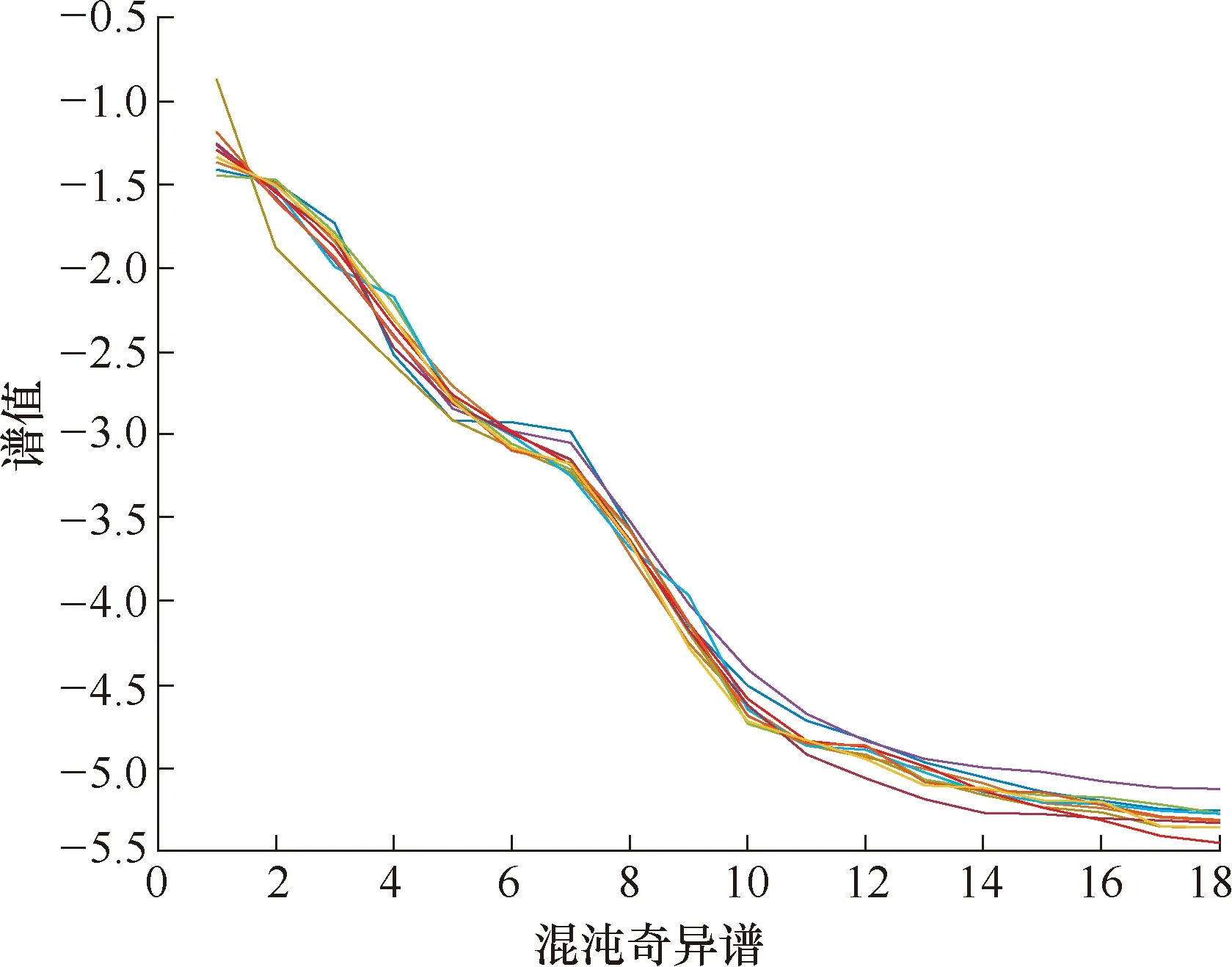
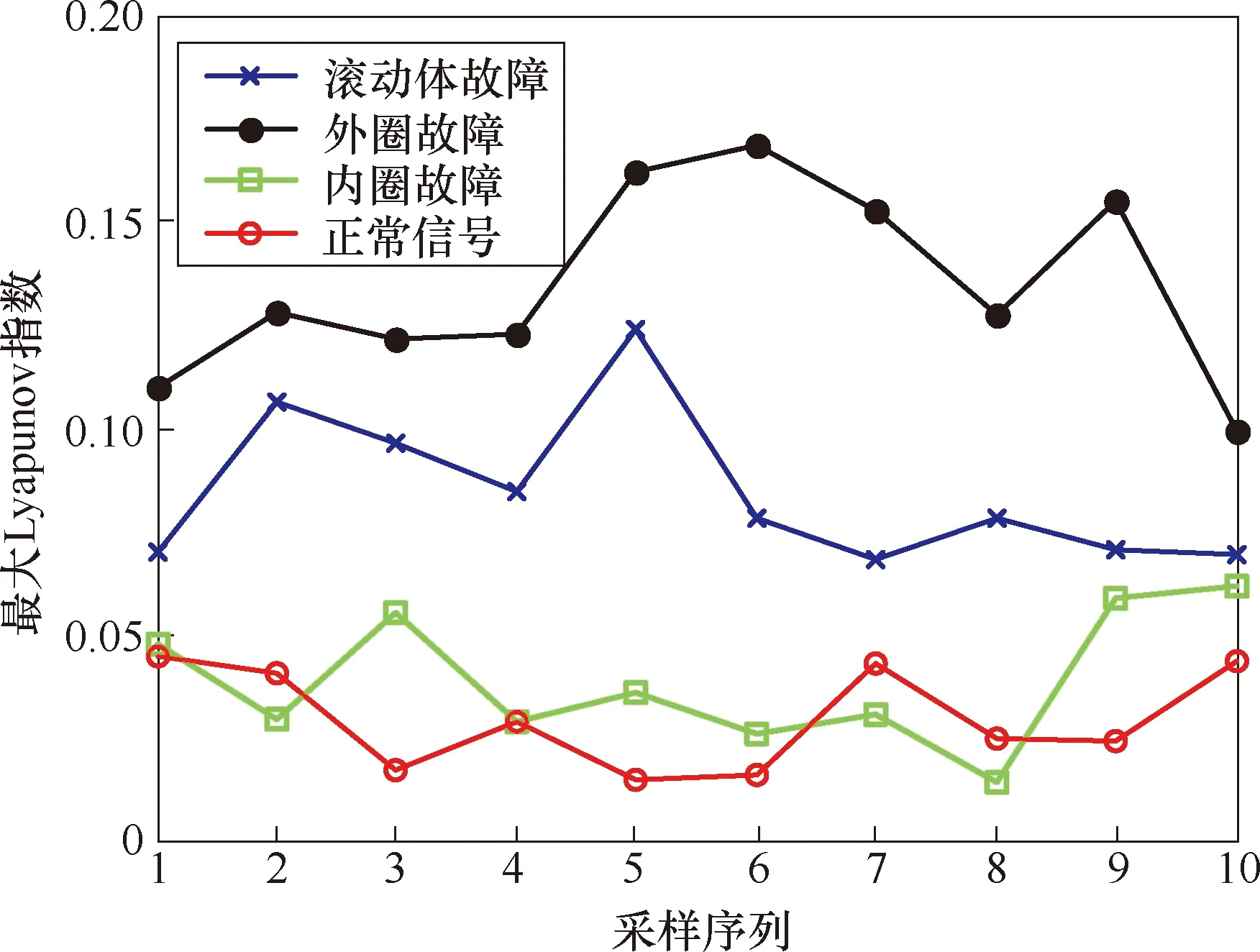
2) 根据E1(i)的波动情况选取一个阈值e，找到第一个Δi

Δi=max(Δi);n≤i≤N-1

(9)

3) 重新设置：

(10)

4) 取j≤i≤N-2，当满足Δi>Δi+1，Δi+1>Δi+2，Δi

同理，当用E2(i)、E2(i+1)换成计算式(8)中的E1(i)、E1(i+1)时，可计算出由式(5)、式(6)确定的关于E2(i)的m值。

3.3 基于符号分析的极大联合熵延迟时间求取方法

3.3.1 最佳延迟时间的极大联合熵准则

考虑时间序列x(n)及其延迟时间序列xτ(n)=x(n+τ)，n=1,2,…,N。根据互信息函数的递推公式[11]，两组序列的互信息可表示为

I(X,Xτ)=H(X)-H(X|Xτ)=H(X)+
H(Xτ)-H(X|Xτ)=I(Xτ,X)

(11)

式中：X代表时间序列X(n)；Xτ代表其延迟序列X(n+τ)；H(X)是孤立的X的不定性，H(X|Xτ)是已知Xτ的X的不定性，所以Xτ的已知减少了X的不定性，则I(X,Xτ)的第一极小值处的τ即为最佳延迟时间。并且为了计算I(X,Xτ)，Fraser A M等[12]提出了复杂的划分网格的方法。

互信息I(X,Xτ)表征X和Xτ的相关程度，I(X,Xτ)取极小值时X和Xτ的相关度也极小，即X和Xτ的联合整体不确定度达到极大[13]。

为了保证重构坐标之间最大限度地相互独立，应使X和Xτ联合整体的不确定性达到最大。由信息理论可知，联合熵H(X|Xτ)是X和Xτ的联合整体的不确定性的度量，H(X|Xτ)越大，则X和Xτ联合整体的不确定性也越大。由此推断，联合熵H(X|Xτ)的第一个极大值点即为相空间重构的最佳延迟时间点[14]。

H(X,Xτ)=H(X)+H(Xτ)-I(X,Xτ)

=Const-I(X,Xτ)

(12)

由此可见，H(X,Xτ)和I(X,Xτ)呈近似相反的变化规律。互信息的极小值点即为联合熵的极大值点在理论上得到验证。

因此,通过复杂的划分网格或者进行网格标记求取互信息第一极小值点，从而确定相空间重构最佳延迟时间可以转换为求取联合熵H(X,Xτ)的第一极大值点。联合熵的计算公式[15]可以表示为

(13)

P(xi,xtj)为变量xi、xtj的联合概率分布，由此可见，求取不同延迟时间下的联合熵[16]，找出联合熵的第一极大值点所对应的τ，即为所求的最佳延迟时间点。

3.3.2 符号分析法求取极大联合熵

二进制划分是最简单的一种划分规则，只需给定一个阈值P0，时间序列中大于此阈值P0的取1，否则取0。阈值P0的选取有均值、零值等。则时间序列X(n)最终被转换成符号序列{S(n)}，所得符号序列表征了2种数据元模式，即

(14)

时间序列信号经二进制符号化规则进行处理，其具体过程描述如图1所示。

图1 二进制符号化规则Fig.1 Binary symbolization rule

按照上式进行标记和辨识，则离散的符号替代连续数据的原始时间序列，见图2。

图2 符号化时间序列图Fig.2 Symbolized time series diagram

符号数d可以通过使符号熵最大化来寻找，为了方便起见，将混沌序列的临界点(d+1)的个数置为11，即d=10。且分割长度L取2。

对时间序列X(n)及其延迟时间序列X(n+τ)，n=1,2,…,N，根据上面所介绍的粗粒化符号方法将其编码成能捕获有用定量信息的特殊的十进制数序列Lx(n)和Lxτ(n)，则各个特殊十进制数出现的频率为时间序列分析的指标，即为联合概率P(Lx,Lxτ)，则符号分析法求取的联合熵公式(13)可以改写为

(15)

4 数值验证

为了验证这2种方法结合求取最佳延迟时间和最佳嵌入维数的准确性和优越性，对常见的典型混沌时间序列Lorenz进行数值仿真,求取这两种典型混沌系统的最佳延迟时间和最佳嵌入维数并画出其吸引子的重构。

Lorenz系统的数值仿真实验如图3所示。

图3 Lorenz系统(σ=16, b=4, r=45.92)的数值仿真实验Fig.3 Numerical simulation experiment of Lorenz system (σ=16, b=4, r=45.92)

该系统方程可描述[17]为

(16)

式中：x、y、z分别是三维坐标；σ=16；b=4；r=45.92。

选取Lorenz系统参数确定情况下该系统为混沌系统，用Runge-Kutta法求解方程(16)，步长h=0.01，取变量x为研究对象，去除前8 000个暂态点，得到一个7 000个点的时间序列。

通过本文所提出的符号分析法求取该系统时间序列联合熵H(Lx,Lxτ)的极大值点，求取时间序列的有效延迟时间的图形如图3(a)所示。从图中可以看出，联合熵H(Lx,Lxτ)在τ=11时取得第一个所对应的极值点，故可得由联合熵第一极大值点法求得的相空间重构最佳延迟时间；试验过程中也大大地简化了其计算量。图3(b)是由Cao方法求得的E1&E2的最佳嵌入维数，图3(c)是由改进后Cao方法求得E1的最佳嵌入维数，图3(d)是由改进后Cao方法求得E2的最佳嵌入维数，从图3(b)中可以看出E1、E2都在m大于3后看似不再发生变化，实际m在3之后有微小波动，经过本文提出的改进Cao算法，取e=0.1,如图3(c)确定出E1的最佳嵌入维数为m=12，如图(d)E2的最佳嵌入维数为m=18，所以该时间序列的最佳嵌入维数为18；图 3(e)是m=12时LorenzX相三维重构吸引子图；图3(f)是m=12时的重构吸引子图；图3(g)是m=18时LorenzX相三维重构吸引子图；图3(h)是m=18时的重构吸引子图。从图中可以看出m=12时Lorenz混沌时间序列在X相的三维重构吸引子图和平面的重构吸引子图都无法完全展开，而m=18时重构图能够很好的反映出Lorenz系统的双圈拓扑结构。从而验证了改进Cao算法确定最佳嵌入维数的有效性和优越性。

5 混沌奇异谱特性分析

5.1 混沌奇异谱特征量化分析

由嵌入定理Takens可知，对于混沌时间序列x(t)，可以得出m维相空间的重构吸引子。于是可以得到轨道矩阵：

(17)

式中：N=n-m-1为相点个数，每一个相点坐标为

X(j)=[x(j),x(j+τ),…,x(j+(m-1)τ)]

(18)

设混沌动力系统的m个状态变量相互独立且相互正交，状态空间分布在m维嵌入空间向量的主分量方向上，则存在变换矩阵A，使得YTTT的协方差矩阵为对角阵，即

(19)

式中:CX和CY分别是和的延时-协变矩阵，Sj(j=1,2,…,m)为CY特征值。将特征值由大到小排列，即S1≥S2≥…≥Sm，记

(20)

称S1≥S2≥…≥Sm为系统的奇异谱，它表示各个状态变量在整个系统中所占能量的相对关系。式(20)中对于延时-协变矩阵CX定义为

(21)

式中：c(j)表示延时为时x(n)的协方差，其计算公式如下：

(22)

由协方差公式可知，矩阵CX是一个正定对称矩阵，因此其特征值非负，即e1≥e2≥…≥em>0，这些特征向量Ek称为经验正交函数(EOF)，第k个主成分(PC)定义为混沌时间序列x(t)在第k个经验正交函数Ek上的正交投影系数。从频谱上来看，一个EOF对应着一个自适应滑动平均滤波器，每一个PC代表着信号的特征成分。奇异谱的意义在于：通过它把时间序列信号向嵌入维数主轴分解，信号主成分的大小分布反映出信号能量在对应嵌入维数主轴上的大小分布情况。

5.2 奇异谱的特性验证

针对Lorenz系统，取m=18。实验采用10对分量不同时刻的时间序列，序列点数为5 000，分别对每条序列进行相空间重构，计算奇异谱，将10对奇异谱对应的主成分分量放在同一个谱图中，实验结果如图4所示。

图4 Lorenz系统x分量的10对奇异谱图Fig.4 10 pairs of singular spectra of the x component of the Lorenz system

以x分量时间序列{xn}(n=1,2,…,N,N为时间序列长度)为研究对象。向时间序列{xn}添加10 db噪声，采用m=18，τ=11。取x(t)在不同时刻的10对时间序列，每个序列点数为5 000，然后分别对每个序列进行相空间重构，计算奇异谱，将10对奇异谱对应的主成分分量放在同一个谱图中，实验结果如图5所示。

图5 Lorenz系统x分量的10对含10 db噪声的奇异谱图Fig.5 10 pairs of singular spectra with 10 db noise for the x component of the Lorenz system

接着再对Lorenz系统中x方向的一条时间序列，点数为5 000，分别加入10 db～20 db噪声。采用m=18，τ=11。计算其奇异谱，得到奇异谱图如图6所示。

图6 Lorenz系统x分量的不同噪声含量的奇异谱图Fig.6 Singular spectrum of different noise content of the x component of the Lorenz system

从图4、图5和图6可以看出，奇异谱分析不仅具有很强的稳定性及抗噪性能，还能将不同信号明显区分。一方面对于含有噪声的信号可以成功提取有用信息，另一方面可以将不同的有用信息有效区分。

6 混沌奇异谱分析在滚动轴承故障诊断中的应用

6.1 轴承振动信号的混沌判别

首先，对4种轴承状态振动信号选用10对不同时间段的样本，时间序列的长度为2 400；然后，用本文方法分别计算样本序列的嵌入维数和延迟时间，将它们作为小数据法的输入，从而估计出样本序列的最大Lyapunov指数。

图7为不同状态的最大Lyapunov指数，观察可知不同状态下振动信号的时间序列的最大Lyapunov指数均大于0，表明振动信号具有混沌特性，可以利用混沌相关理论对其进行分析。

图7 不同状态下的最大Lyapunov指数Fig.7 Maximum “Lyapunov” index in different states

6.2 轴承振动信号的奇异谱

从图7中可以看出，不同时间段的外圈故障的最大Lyapunov指数波动比较大，正常状态和内圈状态下时间序列的最大Lyapunov指数交织在一起，仅利用设置临界值的方法很难直接将不同状态的信号分开。故需要有效的特征提取方法提取故障特征。

针对4种轴承类型下的振动信号，每种选择50个样本，样本长度均为2 400，采用本文提出的混沌奇异谱方法。将数据代入嵌入维数的Cao方法和基于符号分析的极大联合熵求延迟时间的方法，取所有数据的最大嵌入维数和延迟时间，计算奇异谱，最终相空间重构过程中选用m=15，τ=6，每种类型随机选取4个序列，绘制4种振动信号的奇异谱图如图8所示。

图8 不同损伤位置的奇异谱图Fig.8 Singular spectrum of different damage locations

从图8中看出，不同损伤位置对应奇异谱图能量分布明显不一致，但相同故障类型的奇异谱图分布较为一致，上下波动不大，各个主成分的谱值基本一致，说明同一故障类型的轴承振动信号具有比较稳定的奇异谱。所以，混沌奇异谱可以代表不同损伤位置振动信号的内在动力学特征。

为了确定上述实验效果，选择电机驱动端振动传感器采集的正常状态、不同位置损伤、不同损伤直径等10种状态下的振动信号，采样频率为12 kHz，转速为1 772 r/min，负载为0.735 N·m，下面实验中的振动信号都是采取时间为0.2 s，共2 400个采样点。

采用混沌奇异谱对驱动端轴承10种运行状态进行故障诊断，每种运行状态选50组无重叠数据，每组数据的长度为2 400。首先计算10组原始振动信号数据的混沌奇异谱，将数据代入求嵌入维数的Cao方法和基于符号分析的极大联合熵求延迟时间的方法，取所有数据的最大嵌入维数和延迟时间，最终相空间重构过程中嵌入维数选用m=20，时间延迟选择τ=6，进而产生500×20的矩阵，为不同运行状态的数据贴上标签，状态类别依次为1，2，3，4，5，6，7，8，9和10。每种运行状态得到50个特征样本，其中30个作为训练集，剩余20个作为测试集，训练集样本都是采用的有标签样本。图9是10种状态的混沌奇异谱特征向量图。

图9 10种状态的混沌奇异谱特征向量Fig.9 Chaotic singular spectral eigenvectors of 10 states

从图9中看出，不同运行状态下的振动信号的混沌奇异谱特征都是前期谱值较大，后期谱值较小。同时，不同运行状态的混沌奇异谱特征前期谱值相差很大，后期谱值却相差不大，谱值的大小代表能量的分布，说明运行状态发生改变后系统的能量分布也发生了改变。

由此可见，不同的故障类型和不同的故障尺寸，均可通过奇异谱分析提取有效的特征，并且有效地区分，说明奇异谱分析可以有效地应用于机械故障诊断。

7 结 论

(1) 混沌奇异谱作为一个有效的特征提取方法，能够将信号中的不同成分通过相空间重构后以图形的形式进行了有效区分，线型区分明显，具有很好的准确性及可观性。

(2) 针对混沌奇异谱分析时间序列的延迟时间和嵌入维数存在的不足，利用基于符号分析的极大联合熵方法，采用Cao改进算法确定嵌入m，提高了准确度，两者准确实现相空间重构，取得了很好的准确性、稳定性及实效性。

(3) 研究表明，机械故障信号具有混沌的特性，本文方法已在滚动轴承早期故障识别中应用，为机械故障早期诊断提供一种新的有效途径。