5G超密集网络下的室内压缩重构指纹定位算法
贾鹏飞,张月霞,b,c
(北京信息科技大学 a.信息与通信工程学院;b.现代测控技术教育部重点实验室;c.高动态导航北京市实验室,北京 100101)
0 引 言
随着位置服务的兴起和广泛应用,用户对室内定位的精度提出了更高的要求。而随着第五代移动通信技术的发展,5G将实现超密集网络部署[1],大幅提高基站密度,使用户可以同时与多个基站进行通信,有利于多基站协作定位,从而使定位精度提高至亚米级,更好地满足人们对于室内高精度定位的需求。
传统的室内定位算法[2-5]都是基于测距的定位方法,在5G超密集网络下其定位精度会受到影响,不能达到较高定位精度要求。而指纹匹配定位算法是预先构建定位所需的指纹库,再将待定位点的数据通过指纹匹配算法与指纹库中的数据进行匹对,从而估计待定位点的位置坐标,其定位精度较高。许多学者对指纹匹配定位算法做了大量研究。Horsmanheimo等人[6]设计并实现了一个基于5G的室内定位平台,采用了精细定时测量技术,可通过多边计算来计算位置估算值,实现了基于图像的定位和基于RSSI的指纹识别。文献[7]提出了一种基于K-means和支持向量机(Support Vector Machines,SVM)的蓝牙室内定位算法,利用卡尔曼滤波和K-means算法对收集到的数据进行处理,最后通过SVM模型完成待测数据的分类,算法的定位精度稳定在1.5 m以内。这些指纹匹配算法虽有不错的定位精度,但其指纹库数据相对较少,不容易构建。在5G超密集网络中,参与定位的基站多,所需测量的数据量庞大,因此如何降低指纹库数据构建的复杂度并提高定位精度成为了当前亟待解决的问题。
本文提出一种5G超密集网络下的压缩重构指纹定位算法。该算法首先测量部分指纹库数据,通过非精确增广拉格朗日算法(Inexact Augmented Lagrangian Multiplier,IALM)进行矩阵填充,将该指纹库矩阵重构为完整,然后利用加权K近邻(Weighted K-Nearest Neighbor,WKNN)算法实现待定位点的在线匹配。
1 超密集网络室内定位模型
假设5G超密集网络室内定位模型如图1所示,基站分布在模型顶部,总个数为N,u为待定位点,分布在空间中任意位置。

图1 5G超密集网络室内定位模型
为了给用户提供更好的服务,提高定位精度,需对基站部署进行划分。设基站分布满足齐次泊松点过程[8],那么基站服务范围则可以用泰森多边形(Voronoi diagram)来表征。
设每个基站的通信半径为r,则基站的密度为
(1)
式中:S为模型顶部面积。根据文献[9],基站密度λ>>1 000 cell/km2。
根据齐次泊松点过程,基站的概率分布为
(2)
图1中顶部基站服务区域分布如图2所示,横纵坐标表示平面区域内长和宽,其中每一小格代表10 m,即平面范围为100 m×100 m,绿点代表基站位置且服从泊松分布,绿色区域表示泰森多边形覆盖范围。
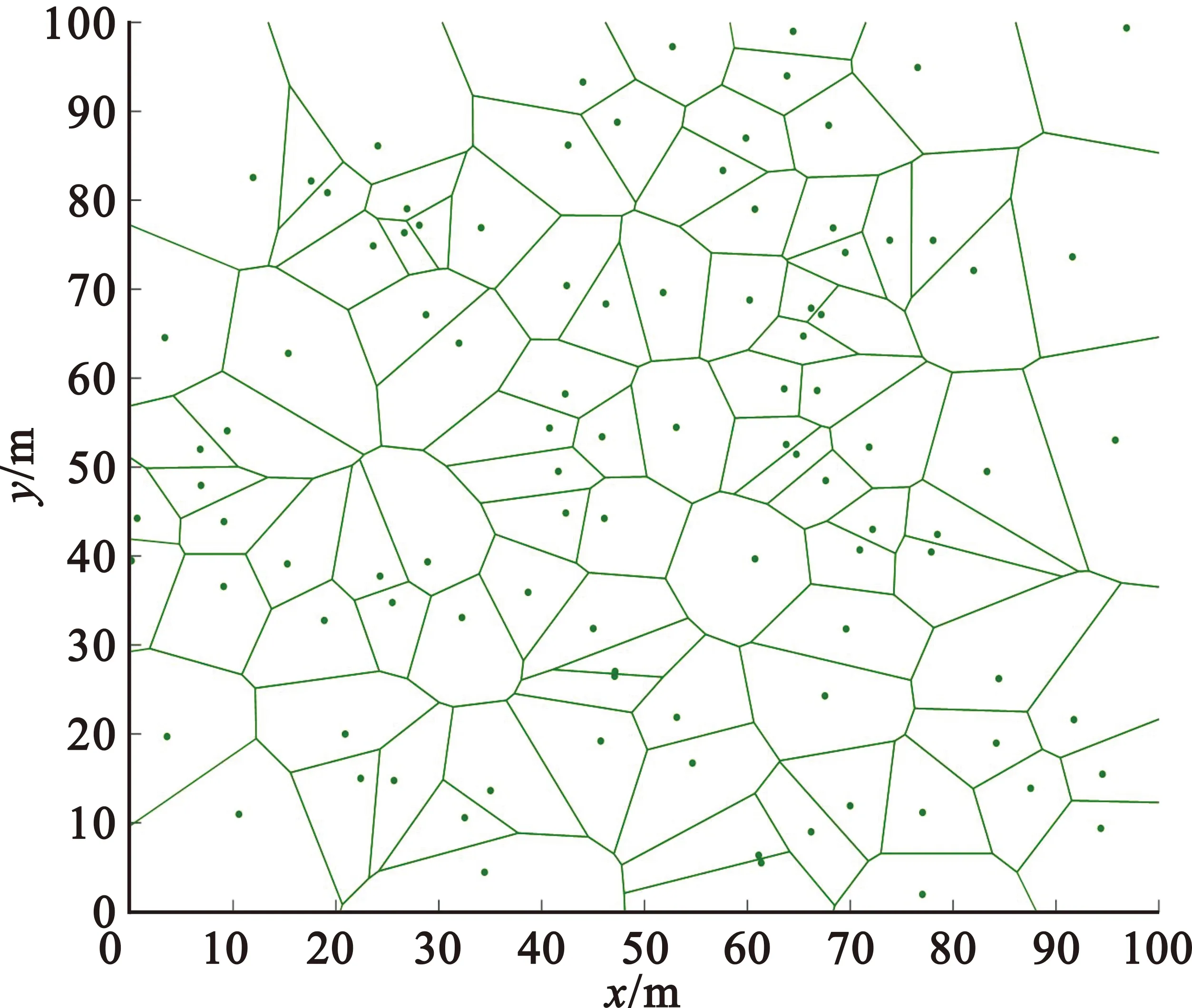
图2 基站服务区域表征图
2 指纹匹配算法
2.1 离线建库阶段
2.1.1 指纹库组成
在室内空间中任意一点其对应的数据为指纹数据库中的数据点,即指纹。设指纹点共n个,由于n趋于无穷大,在实际采集中获取所有的指纹数据几乎不可能,因此,设定指纹点在空间中均匀分布,且每个指纹间存在较小的间距d,这样就可以将n限定为一个有限的值n′,那么指纹点的集合可以用L={l1,l2,l3,…,ln′}表示。以la点为例,该点坐标为(xa,ya,za),其指纹表示为
S=[RSSI1a,RSSI2a,RSSI3a,…,RSSINa]T。
(3)
那么离线建立的指纹库可以表示为一个N×n′的矩阵M:
(4)
2.1.2 矩阵填充算法
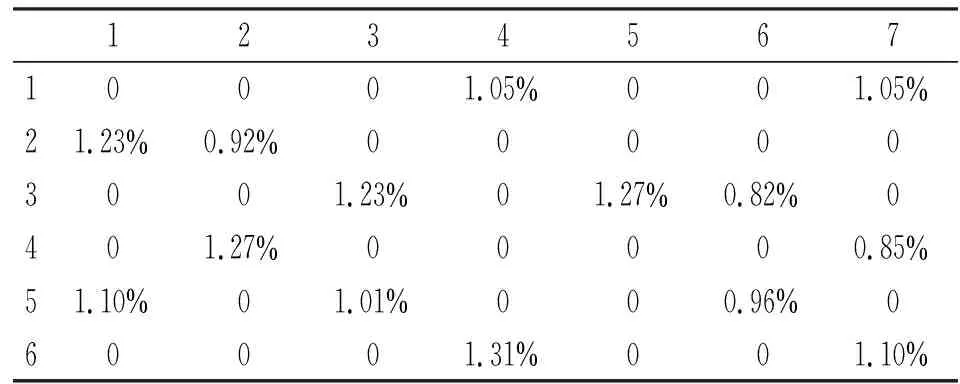
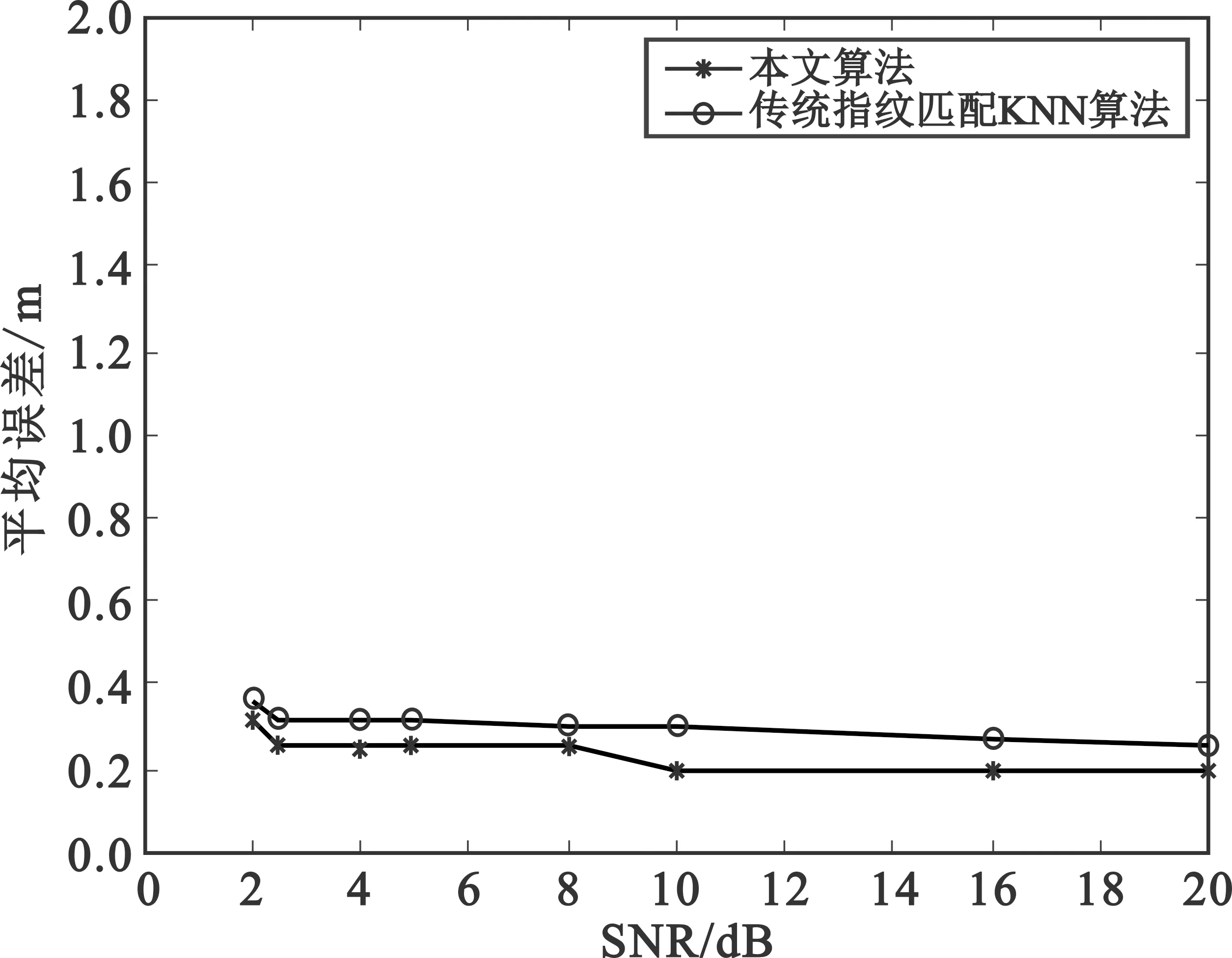
设Ω是指纹库矩阵M的一个子集,Ω中只含有m个元素Mij,Mij为M中观测到的元素,其中Mij∈M,m< 定义:PΩ为Ω上的投影算子,则有 (5) PΩ(M)在Ω集合上等于Mij,在Ω的补集上等于0,则矩阵M中的已知元素可以用投影PΩ(M)来表示。在一定约束条件下,矩阵填充问题可以用如下秩函数最小化模型来表示: min rank(X) s.t.PΩ(X)=PΩ(M)。 (6) 式中:rank(X)表示X的秩,X为填充矩阵。 但式(6)为非凸函数,因此该问题是一个NP-hard问题,求解极为困难。为此Recht等人在文献[10]中提出用矩阵核范数最小化问题代替式(6)。核范数定义为 (7) 式中:‖X‖*表示X的核范数,σk(X)表示X的第k大奇异值。由于核范数是一个凸函数,因此矩阵填充问题可以转化为如下最小化问题来求解: min ‖X‖*s.t.PΩ(X)=PΩ(M) 。 (8) 本文采用ALM[11]算法对该问题进行求解。 将式(8)进行变形为 min ‖X‖*s.t.X+E=M,PΩ(E)=0 。 (9) 式中:E为矩阵X与原始矩阵M间的差,增加约束条件即PΩ(E)=0时,等式PΩ(X)=PΩ(M)成立。该算法的增广拉格朗日函数为 (10) 式中:μ为增广拉格朗日函数的惩罚因子,Y为矩阵变量。 ALM算法交替更新X、E、Y、μ,迭代公式如下: (11) 由于IALM[11]不需要精确求解,只需一次迭代就可以达到较高精确度,故本文采用了IALM算法进行矩阵填充应用,其算法伪代码如下: 1 给定观测矩阵之PΩ(M),Y=0,E=0,k=0 2 while不收敛 4Xk+1=USμk-1[S]VT 6Yk+1=Yk+μk(M-Xk+1-Ek+1) 7μk+1=ρμk+1 8k=k+1 9 end 输出:Xx+2 本文采用卡方距离计算待定位点与参考指纹点的相似度,并对其进行加权处理,采用加权K近邻(Weighted K-nearest Neighbor,WKNN)算法[12]对待定位点进行指纹匹配。 Step1 计算待定位点与指纹库中参考点间的卡方距离dj: (12) 式中:RSSIij是第j个参考指纹点的第i个RSSI值,RSSIj是待定位点的第j个RSSI值。 Step3 对集合D中的K个距离进行加权处理,得到相应的加权系数ωi: (13) 式中:δ是一个较小的正数,是为了避免分母为0。 (14) 式中:(xi,yi,zi)是对应参考点的指纹位置坐标。 RSSI=P+gain-loss-noise。 (15) 式中:P表示基站信号发送功率,gain表示信道增益,loss表示路径损耗,noise表示高斯白噪声。 在指纹库的构建中,先通过常规方法得到原始指纹库M,然后对M进行随机采样60%的数据用以恢复剩余40%的数据以得到重构后的指纹库X。 由于指纹库数据过大,仅提供指纹点的1~7号指纹数据进行数据对比。原矩阵中的指纹数据如表1所示,重构指纹库数据如表2所示,重构矩阵与原矩阵中数据的绝对误差如表3所示。 表1 原指纹矩阵数据表 表2 重构指纹矩阵数据表 表3 误差矩阵数据表 由表3可知,重构矩阵与原始矩阵间存在一定误差,根据全部矩阵数据间的对比计算可得其平均误差为1.13%,说明IALM算法可以很好地恢复原始矩阵。 设信噪比为10 dB,使用WKNN算法进行指纹匹配定位,得到如图3所示定位结果。由图可看出,本文算法定位结果与真实位置高度重合,具有较高的精确度。 图3 三维定位结果图 本文定位算法与传统KNN算法平均误差对比如图4所示,可以看出,本文指纹定位匹配算法随信噪比的增加,平均误差呈递减趋势,整体定位误差要小于传统指纹匹配算法,且在信噪比为10 dB时达到误差最小(0.200 8 m),证明该算法具有良好的定位精确度。 图4 平均误差对比分析图 本文提出的5G超密集网络室内压缩重构定位算法,首先构建部分指纹库数据,然后通过矩阵填充IALM算法重构出完整指纹数据库,在误差为1.13%的情况下节约了40%的工作量。仿真实验表明,本文提出的指纹定位算法相较于传统指纹KNN匹配算法减少了指纹库构建采集的工作量,且定位结果更好,在10 dB信噪比时误差达到最小,为0.200 8 m。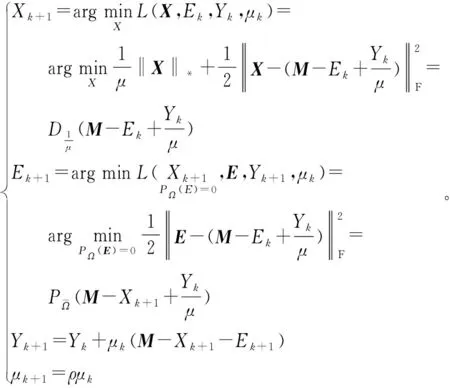
2.2 在线匹配阶段


3 仿真分析

3.1 指纹库矩阵填充误差分析


3.2 定位误差分析

4 结 论

