事件触发控制下具有时滞和干扰的多智能体系统固定时间二部一致性∗

魏小杰，蒋海军，于志永

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046)

0 引言

多智能体系统(MASs) 是近几十年来分布式人工智能发展的重要分支,可以用于解决复杂的实际问题[1−2].一致性作为MASs 中有代表性的群体行为[3],是指所有智能体在适当的控制协议下达到相同的状态.在实际应用中,系统中可能同时存在竞争和合作的行为,例如多机器人团队的运动比赛等[4−5].因此文献[6] 研究了具有拮抗行为的MASs 二部一致性.

在一致性研究中,收敛速度是衡量一致性行为的重要指标.与渐进收敛性相比,固定时间收敛性更加符合实际应用.因此,基于文献[7] 中给出的固定时间稳定性理论,通过设计连续的控制器,文献[8] 研究了系统的有限时间和固定时间二部一致性.为了减少控制过程中的能源消耗,文献[9] 提出了事件触发控制方法.在文献[10]中,通过设计事件触发控制算法研究了具有时滞和外部干扰的MASs 固定时间一致性.然而,很少有学者研究事件触发控制协议下具有时滞和干扰的MASs 二部一致性.

本文的主要内容总结如下:(1) 基于事件触发控制方法设计了具有时滞和干扰的MASs 分布式控制协议.(2) 运用代数图理论、固定时间稳定性理论,给出MASs 实现二部一致的相关准则.(3) 为了避免符号函数在控制中产生的抖振现象,设计了具有饱和函数的事件触发控制协议,并证明系统在提出的两个控制协议下不会产生Zeno 行为.

1 模型建立及预备知识

在本文中,RN和RN×M分别表示N 维实数向量空间和N×M 维实数矩阵空间.对于实对称矩阵G,G>0(或G<0) 表示G 是正定(或负定)矩阵,GT表示矩阵G 的转置.sign(·) 表示符号函数.‖·‖ 表示向量的2-范数或矩阵的2-范数,|·| 表示向量的1-范数或标量的绝对值.

考虑由M 个智能体组成的网络.其中网络拓扑由无向有符号图G 表示,G 是一个三元组G={V,E,A},其中V={v1,v2,···,vM} 是节点集,E ⊆V×V 是边集,A=[aij]∈RM×M是邻接矩阵.若(vj,vi)∈E,vi和vj互为邻居,则aij/=0 并且记vi的邻居节点集为Ni={j:(vj,vi)∈E}.假设网络拓扑G 是无向的且不含有自环,则有aij=aji,aii=0(i,j=1,2,···,M).记节点的度矩阵为H=diag(h1,h2,···,hM),hi=定义拉普拉斯矩阵L=[lij]∈RM×M为L=H−A.L 的元素表示如下

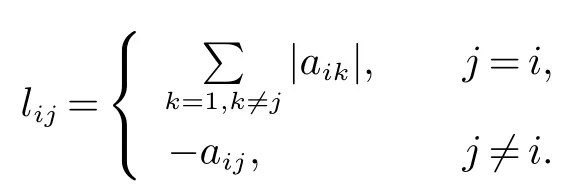
如果对于任意的两个节点vi和vj之间存在路径,则称无向有符号图G 是连通的.如果可以将顶点集V 划分为满足条件V1∩V2=Ø 和V1∪V2=V 的子集V1和V2,并且子集V1(或V2) 中的内部节点vi和vj之间保持合作关系,即aij≥0,而子集V1和V2中的节点存在竞争关系,即对∀vi∈V1,vj∈V2有aij<0,则称图G 是结构平衡的.否则,称符号图G 是结构不平衡的.

引理1[6]若结构平衡符号图G 的邻接矩阵为A ∈RM×M，则存在一个规范变换U=diag(σ1,σ2,···,σM)(σi∈{−1,1}),使得UAU 的项都是非负的.

注1在MASs 二部一致性中,结构平衡是网络拓扑必须满足的条件,如果符号图G 结构不平衡,则MASs 会收敛到同一状态,不会达到二部一致.该结果也会在数值模拟中被验证.

引理2[6]定义一个新的拉普拉斯矩阵LU,其元素表示如下

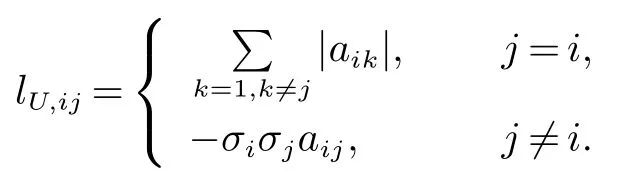
则L 和LU有相同的特征值.

引理3[11]对无符号的连通无向图其拉普拉斯矩阵满足下列性质:

(3) 若1Ts=0,则有≥λ2sTs.

注2对符号图G,因为邻接矩阵A 既有正权重又有负权重,则拉普拉斯矩阵L 不满足行和为零.因此,引理2 定义了一个满足行和为零的新拉普拉斯矩阵LU,那么二部一致性问题可以转化为一般的一致性问题来解决.

设第i 个智能体的动力系统为

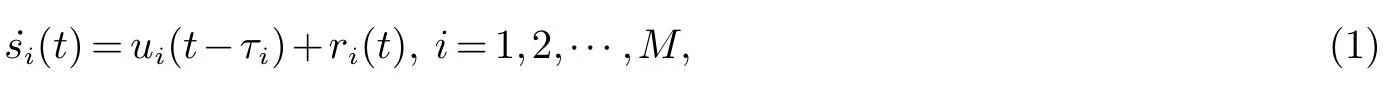
其中：si(t),ui(t),τi,ri(t)(i=1,2,···,M) 分别代表第i 个智能体的状态信息,控制输入,时滞和未知干扰.

假设1存在一个正的常数r,使得

定义1对于MASs (1),如果存在一个不依赖系统初始状态的有界常数T >0,满足−σiσjsj(t)|=0,i=1,2,···,M,且对于t>T 时,有si(t)=σiσjsj(t),则称系统(1) 在固定时间内达到二部一致.记T 为停息时间估计.

引理4[7]对于MASs (1),存在一个连续的径向无界函数F(t),满足下列不等式:≤−µFp(s(t))−νFq(s(t)),其中µ,ν >0,p ∈(0,1) 且q ∈(1,∞).那么系统(1) 在固定时间T(s) 内达到一致,并且T(s) 满足T(s)≤Tmax=此外,若对F(t)存在一个常数ω>0 满足不等式˙F(s(t))≤−µFp(s(t))−νFq(s(t))+ω,则称系统(1) 达到了鲁棒固定时间一致.

引理5[12]对于常数ξ1,ξ2,···,ξK≥0,有下列不等式成立

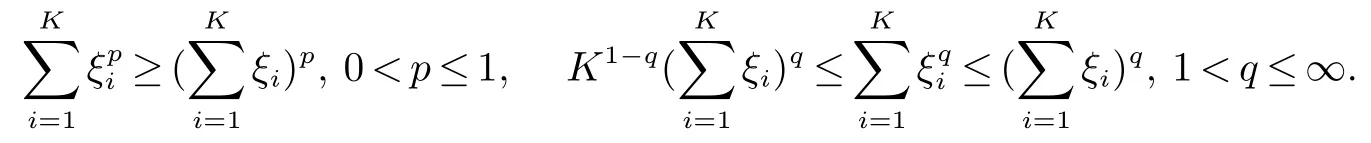
2 主要结论

首先,利用事件触发控制方法,构造第i 个智能体的控制输入如下

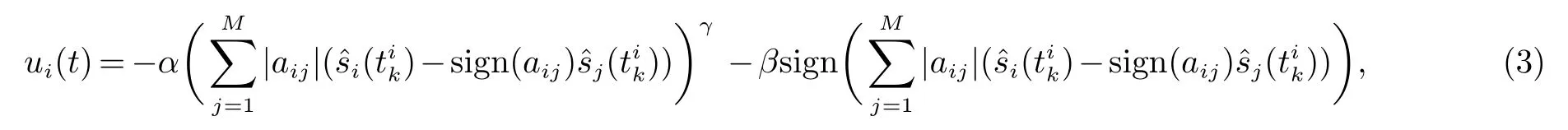
为了简化(3),定义yi(t) 为

因此，事件触发控制器可以简化为

定义测量误差为

构造第i 个智能体的触发函数为

定理1对于MASs (1),考虑具有触发函数(8)的控制协议(6),若假设1 成立而且网络拓扑G 是结构平衡且无向连通的有符号图,当控制增益α 和β 满足

则MASs (1) 可以实现固定时间二部一致,且停息时间T(s) 估计为

其中：a>0,b>0 是常数,γ ∈(1,∞).

证明构造一个新变量

根据引理2 和引理3,有以下不等式成立

其中：λ2和λM是LU的最小非零特征值和最大特征值.

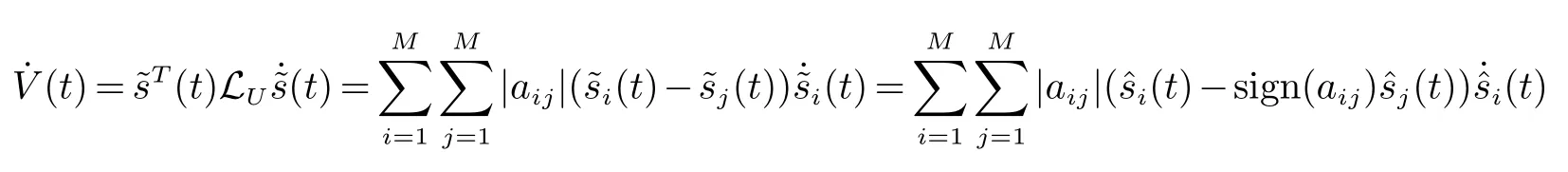
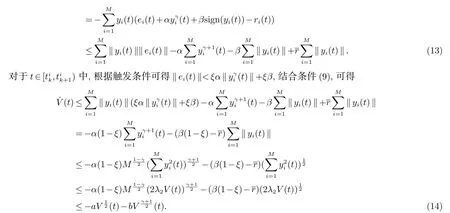
根据引理4,可以得到

注3从定理1 可以看出,固定时间稳定性理论下的停息时间与系统的初始值无关.与文献[8] 相比,本文创新的地方是在动力学系统中考虑了时滞和干扰的影响,并采用了事件触发控制方法研究MASs 的固定时间二部一致性.

下面我们证明事件触发控制器(3) 下MASs 不会产生Zeno 现象.

定理2对于MASs (1),若定理1 的条件成立,则触发函数(8) 不会发生Zeno 行为.

证明由(12) 式可得≤2λMV(t)≤2λMV(0),其中V(0)=

进一步,求ei(t) 的右上导数,可得

φ1和的定义如下

由触发条件gi(t)≥0,有

注4在控制协议(3) 中使用了符号函数,当误差趋于0 时,控制ui(t) 会产生振荡现象.为了克服这一不足,引入饱和函数进一步改进控制器(6).

利用饱和函数，第i 个智能体的控制器设计成如下形式

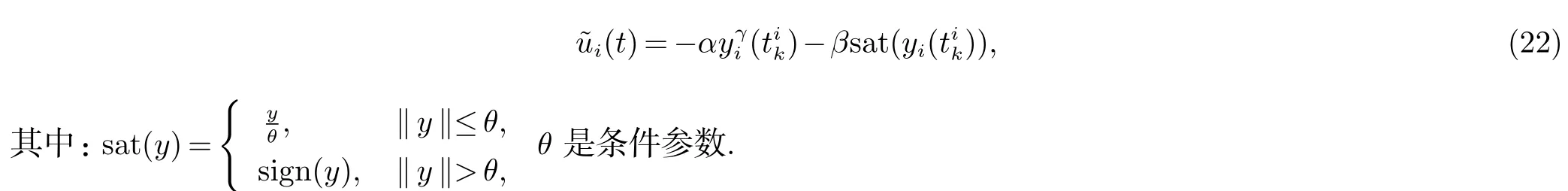
第i 个智能体的测量误差和触发函数分别表示为以下形式

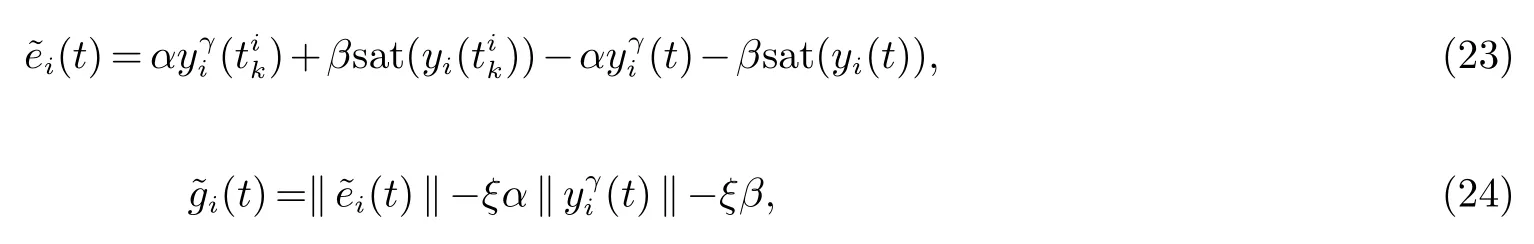
定理3对于MASs (1),考虑具有触发函数(24)的控制协议(22),若假设1 成立而且网络拓扑G 是结构平衡且无向连通的有符号图,其中增益参数α 和β 与定理1 相同,则MASs (1) 可以实现固定时间二部一致性.此外,系统可以避免Zeno 现象.

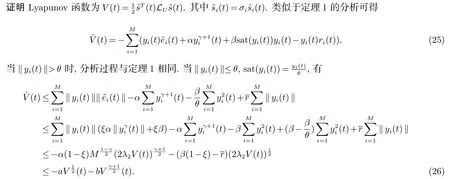
因此,类似于定理1 的分析可知在固定时间内MASs (1) 达到二部一致.

3 数值模拟

考虑由5 个智能体组成的多智能体系统(1),其中结构平衡的网络拓扑如图1 所示,结构不平衡的网络拓扑如图2 所示.图中黑线表示智能体之间的合作关系,红线表示竞争关系.

图1 结构平衡图G1

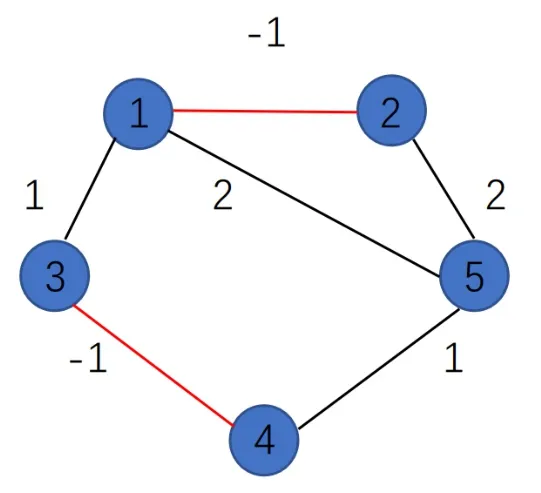
图2 结构不平衡图G2

在系统(1) 中τi=0.03,ri(t)=0.05cos(t),i=1,2,3,4,5,显然,未知干扰满足|ri(t)|≤=0.05.记图G1的拉普拉斯矩阵为L1,通过计算可得L1的特征值λ2(L1)=1.491 4.分别在两个例子中考虑有符号函数和饱和函数的固定时间事件触发控制算法.

例1 (符号函数)对MASs (1),考虑事件触发控制算法(6).其中α=1.138 7,β=0.827 6,γ=ξ=0.6,通过计算,定理1 的条件成立,并且Tmax=10.选取系统的初始条件为:s1(0)=−2;s2(0)=−4;s3(0)=1;s4(0)=5;s5(0)=1.则MASs (1) 的状态如图3 所示.每个智能体的触发时刻如图4 所示.显然,系统在控制协议下能实现二部一致.

图3 si (i=1,2,3,4,5) 的轨线

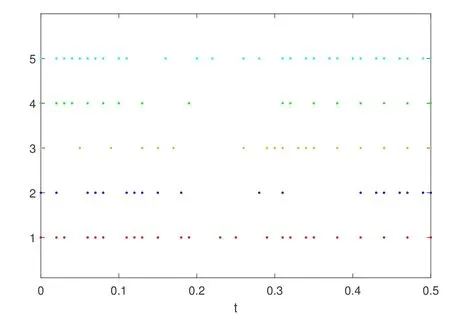
图4 智能体在控制器(6) 和触发函数(8) 下的触发时刻

例2 (饱和函数)对MASs (1),考虑事件触发控制算法(22).其中参数θ=0.01,其他参数取值与例1 相同,可以验证定理3 的条件成立.选取系统的初始条件为:s1(0)=3;s2(0)=−6;s3(0)=3;s4(0)=2;s5(0)=4.则MASs (1) 的状态如图5 所示.每个智能体的触发时刻如图6 所示.

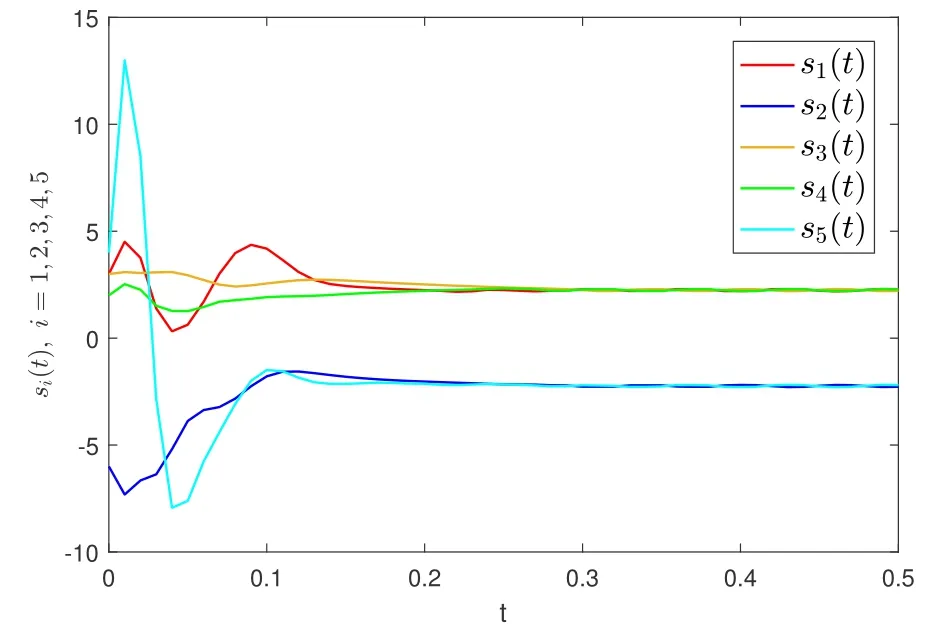
图5 si (i=1,2,3,4,5) 的轨线

图6 智能体在控制器(22) 和触发函数(24) 下的触发时刻

此外,如果网络拓扑是不平衡的(如图2 所示).在控制协议(6)和(22)下,系统的状态轨迹分别如图7 和图8 所示,即所有智能体的状态收敛于同一个值.

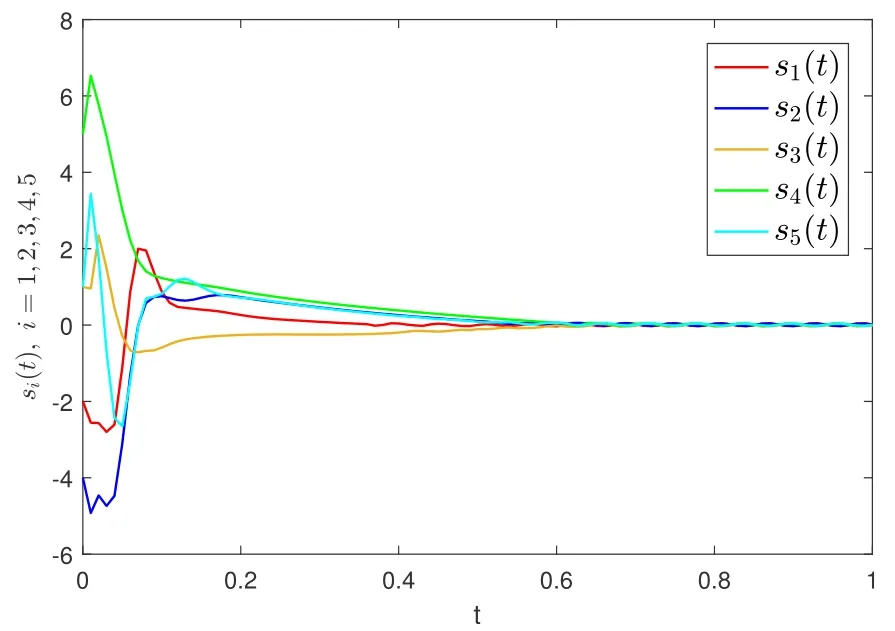
图7 控制协议(6) 下si (i=1,2,3,4,5) 的轨线

图8 控制协议(22) 下si(i=1,2,3,4,5) 的轨线

4 结论

本文基于事件触发控制方法,研究了具有时滞和未知干扰的MASs 固定时间二部一致性.通过设计两种不同的控制协议,并运用固定时间稳定性理论给出MASs 实现二部一致性的准则,证明了在控制协议下Zeno 现象不会发生.最后,给出两个数值例子验证了协议的可行性.