直流馈入对工频变化量距离保护影响分析及改进∗

刘江山，李凤婷，解 超，陈睿康

(新疆大学 电气工程学院，新疆 乌鲁木齐 830047)

0 引言

高压直流输电技术具有远距离、大容量等优势.我国已经建成世界上最大的交直流混联电网，对实现电力跨区传输具有重大意义.但由于交直流电网的强耦合和非线性特性，使得交流系统的单一故障通常会表现出复杂特性，为直流近区域继电保护技术带来了全新的挑战[1−6].

为了研究直流馈入对直流近区域故障特征的影响，文献[7-8]通过仿真研究了不同故障程度下的直流系统注入交流系统等值电流.文献[9]利用动态向量的方法得出直流系统等值工频电流的变化特征，在其基础上文献[10]进一步考虑了直流控制策略切换，研究了更为准确的等值工频电流的变化特征.文献[11]提出在直流系统发生换相失败故障时，直流系统等值工频变化量阻抗呈容性的特征.

直流馈入下的故障特征与纯交流系统具有明显差异，会造成保护的误动，文献[10]和文献[12-14]分别分析了直流馈入下对电流差动保护、距离保护、方向纵联保护的影响并提出了改进措施.工频变化量距离保护作为快速距离保护的I段被广泛应用于交直流电网，但是，针对工频变化量距离保护的研究多集中在纯交流的情况下.文献[15]研究认为工频变化量距离保护的保护范围与保护背侧系统阻抗和保护整定阻抗的比值大小有关.文献[16]提出在实际工作中，保护背后投入的容性阻抗和保护正方向投入的故障限流器将导致工频变化量距离保护误动作.文献[17]研究了风电场实际运行方式的变化及其弱电源特性给工频变化量距离保护带来的影响.文献[18]研究了工频变化量距离保护耐受过渡电阻的能力.文献[19]通过仿真分析了直流馈入对工频变化量距离保护的影响，但缺乏深入的理论分析.文献[20]研究了送端系统故障对工频变化量距离保护的影响.综上所述，现有的研究对于直流馈入下的工频变化量距离保护并未做深入的分析，针对直流馈入工频变化量距离保护的改进措施更鲜有研究.因此，研究直流馈入对工频变化量距离保护的影响机理及其改进措施对保障系统稳定运行具有实际意义.

基于此，本文首先以受端交流系统为研究对象，建立计及直流控制策略的直流系统等值阻抗模型，分析直流馈入下直流系统等值工频变化量阻抗特性，进而深入研究直流馈入下传统工频变化量距离保护正向保护适应性问题.最后提出一种工频变化量阻抗继电器与全阻抗继电器配合使用的策略，并基于PSCAD/EMTDC平台仿真验证理论分析的正确性和所提策略的有效性.

1 工频变化量距离保护基本原理

工频变化量距离保护是一种通过反应突变量工频分量电压、电流而工作的距离保护.其固定门槛动作判据为

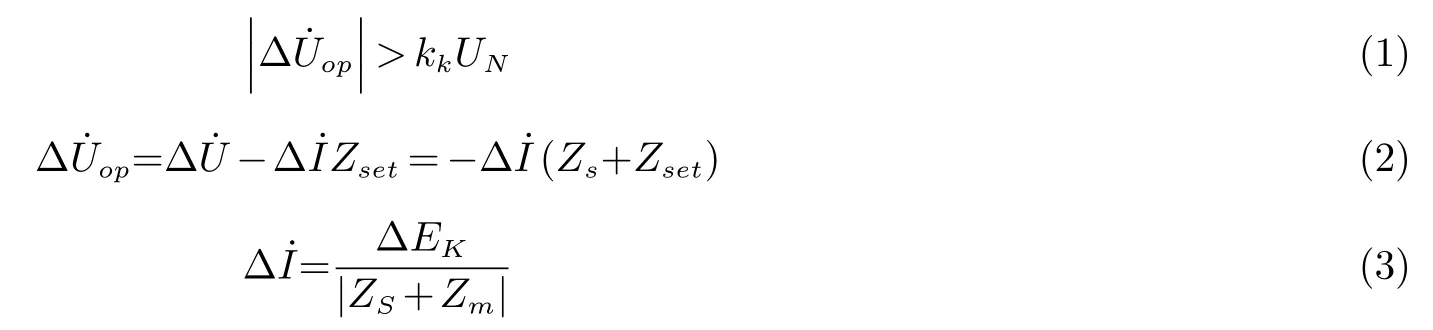
接地故障和相间故障，补偿电压变化量的表达式为

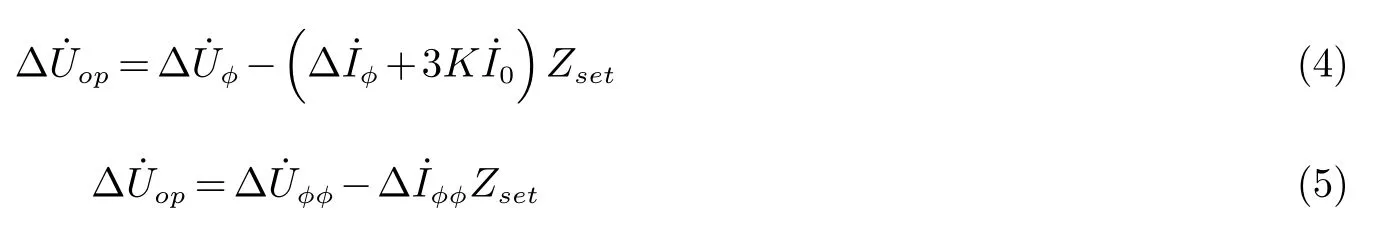
其中：φ为a，b，c；φφ为ab，bc，ca；K为零序补偿系数；为保护安装处零序电流.

在正方向故障时，如图1(a)所示，工频变化量距离继电器正方向阻抗圆以-Zs为圆心，以|Zs+Zset|为半径的圆，其动作方程为

反方向故障时，如图1(b)所示，工频变化量距离继电器反方向阻抗圆以反方向系统阻抗为圆心，以−Zset|为半径，其动作方程为

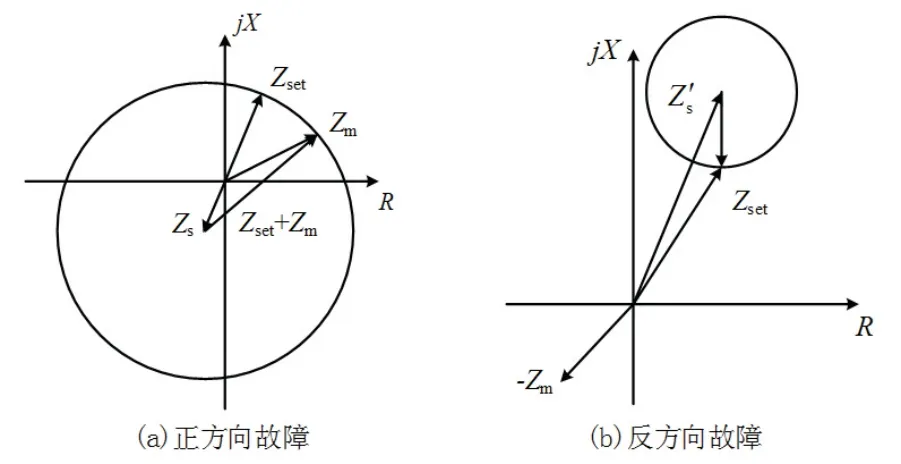
图1 工频变化量距离继电器动作特性Fig 1 Operating characteristics of power frequency variation distance relay

反方向故障时，短路阻抗位于第三象限，而动作区域位于第一象限，保护不动作.综上所述，工频变化量距离保护具有明确的方向性，可作为方向元件使用.

2 直流系统等值工频变化量阻抗特性分析

由上述分析可知，Zs是决定工频变化量距离保护范围的关键.在故障时，交直流系统与纯交流系统的阻抗特性差异很大，导致传统工频变化量距离保护在交直流系统中存在适应性问题.

交直流系统中，系统阻抗是指直流系统在暂态过程中的等值工频变化量阻抗，定义式为

为分析直流系统等值工频变化量阻抗变化规律，采用图2所示交直流系统进行分析[11].

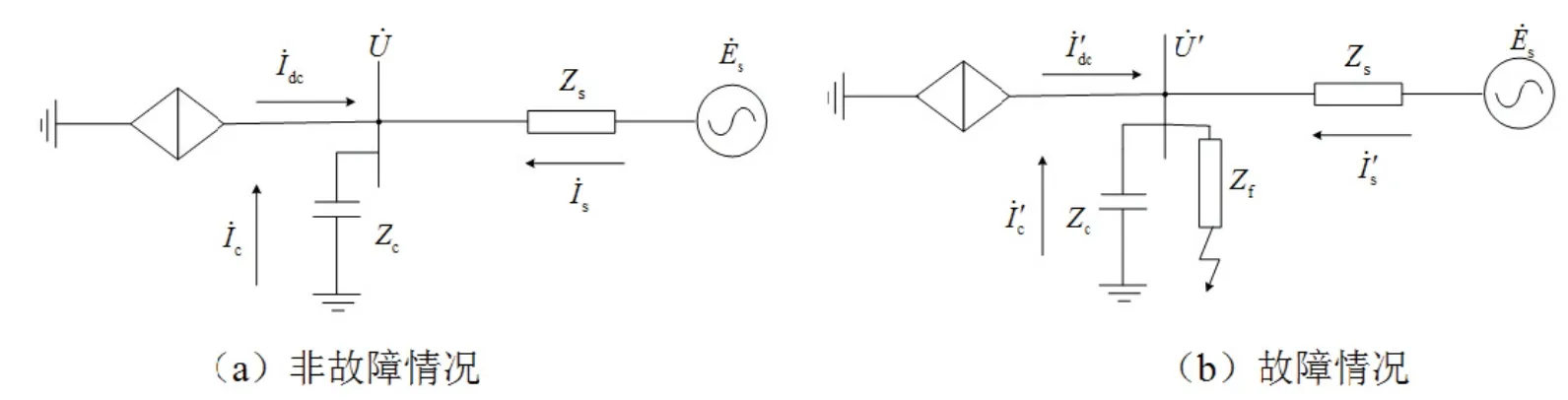
图2 直流馈入交流系统等值电路Fig 2 AC/DC system equivalent circuit

非故障情况下可得

故障情况下

式(11)与式(12)相加可得直流系统等值工频变化量阻抗

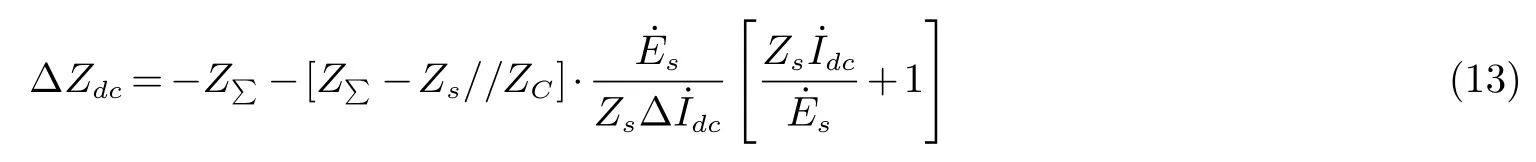
当过渡电阻较大时，对式(13)进行简化可得

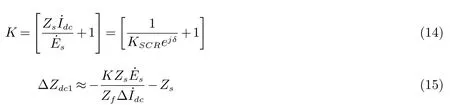
式中：KSCR为短路比，δ为超前的角度.

由于KSCR≫1，所以，K可近似为一个大于1的定值.由式(15)可知，∆Zdc与Zs成正比，而与变化趋势相反.

当过渡电阻较小时，对式(13)进行简化可得

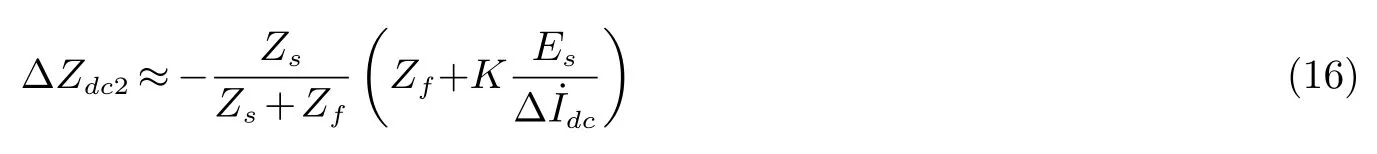
由式(16)可知，随着过渡电阻的减小，Zs/Zs+Zf将趋近于1,Zs对∆Zdc的影响程度降低.对式(15)、式(16)求偏导可得

显然，式(18)的值恒小于式(17)的值，在过渡电阻较小时，对∆Zdc影响更大，∆Zdc的幅值变化将大于过渡电阻较大的时候.

由式(13)、(15)和(16)可以看出，直流系统等值阻抗与系统阻抗、无功补偿装置等效阻抗、等值工频变化量电流等有关系.获取直流系统等值阻抗变化规律的关键是得到故障下逆变侧注入交流系统等值工频电流变化情况，现采用计及控制策略切换的直流系统等效方法对直流系统等值工频变化量电流进行计算.根据动态相量理论可得直流系统注入逆变侧交流系统等值交流电流的P阶相量为[10]

式中：idc是逆变侧直流电流；si为各项电流开关函数；m和n为相应的动态相量的阶数；〈a〉表示动态向量.由于工频变化量阻抗是基于工频变化量电流和电压，所以取n=1，m=1.

逆变侧交流系统故障导致换流母线处交流电压下降，这种情况下，逆变侧直流电压下降并引起直流电流的迅速上升.不同的故障严重程度会导致控制系统动作情况不同，故障暂态期间直流电流特性也会有所差异，如图3所示.

当故障导致直流电压跌落不严重时，即逆变侧直流电压Udc大于0.9 p.u.，VDCOL输出指令值不变，此时整流侧的定电流控制器指令值不变；而逆变器始终采取定关断角控制，随着交流电压的下降，直流电流的上升，逆变器关断角下降，导致CEA主动降低其触发角指令值，以避免换相失败，此举会导致逆变器消耗无功增多，引起故障初期直流电流进一步增大.该情况下直流电流波形见图3中蓝色曲线.

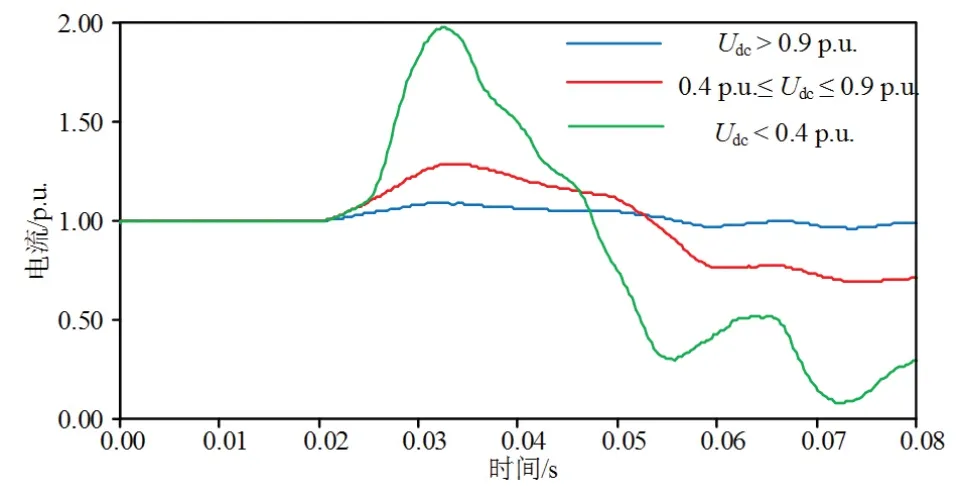
图3 直流电流变化曲线Fig 3 The variation curve of DC current under different faults

当故障导致直流电压进一步跌落时，即0.4 p.u.≤Udc≤0.9 p.u.，VDCOL输出指令值会随直流电压的跌落程度的增加而降低，整流侧的定电流控制器指令值将介于0.55 p.u.∼1.0 p.u..随着交流电压的下降，直流电流的上升，CEA主动调高触发角，进而降低整流侧直流电压，使直流系统两端电压差降低，直流电流减少.该情况下直流电流波形见图3中红色曲线.

当直流电压跌落至0.4 p.u.以下时，VDCOL输出指令值会保持0.55 p.u.不变，整流侧的定电流控制器指令值为0.55 p.u.，CEA同样会调高触发角，使直流电流下降，但由于CEA的指令值与实际电流值相差较大，因此直流电流下降速度会大大加快，该情况下直流电流波形见图3中绿色曲线.

将直流电流代入式(19)中可以得到准确的直流系统等值工频电流.当Udc>0.9 p.u.时，直流系统等值工频电流始终大于正常运行时的电流；当Udc≤0.9 p.u.时，直流系统等值工频电流先增加，后减小至正常运行电流以下.随着Udc跌落程度的增加，直流系统等值工频电流突增的幅值越大，下降速度越快，如图4所示.

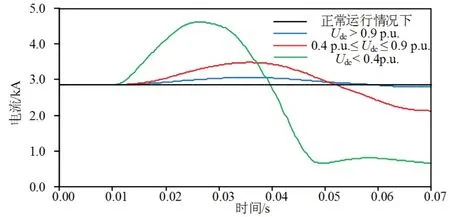
图4 直流系统等值工频电流Fig 4 Equivalent power frequency current of DC system

显然，直流系统等值工频变化量电流的幅值先增大后减小；随着故障严重程度的增加，其增大的幅值也会越大.

逆变侧无功补偿策略为全补偿，逆变侧无功消耗为直流功率的50%∼60%，所以超前.假设电网故障下交流母线电压只有幅值的跌落，并无相位的变化.当过渡电阻较大，故障程度较轻时，直流从受端吸收无功，的幅值变化不大，并向逆时针旋转一个较小的角度，处于第一象限，其相电压、电流相位关系如图5（a）所示，超前，直流系统等值阻抗∆Zdc呈容性，与纯交流系统不同.当过渡电阻较小，故障较严重时，直流从受端吸收大量的无功功率，的幅值会减小，同时向顺时针旋转较大的角度，处于第一或第四象限，其相电压、电流相位关系如图5（b）所示，超前，直流系统等值阻抗∆Zdc呈感性，与纯交流系统相同.

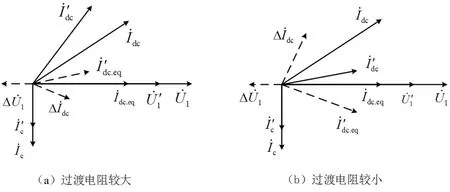
图5 故障情况下电压电流的关系Fig 5 Phasor diagram of currents and voltages for faults

由上述分析可知，在过渡电阻较大时，直流系统等值工频变化量阻抗呈容性，幅值会先减小后增大；当过渡电阻较小时，直流系统等值工频变化量阻抗呈感性，幅值同样会先减小后增大，且会增大到一个较大的阻抗值.等值工频变化量阻抗的幅值、相位特性在过渡电阻较大时与纯交流系统阻抗特性不同，会改变工频变化量距离保护的故障圆特性的圆心位置和半径长度，造成保护不正确动作.

3 直流馈入对工频变化量距离保护影响

联立式(1)、式(2)和式(3)推导可得

等式两边同时除以kkUN/∆Ek

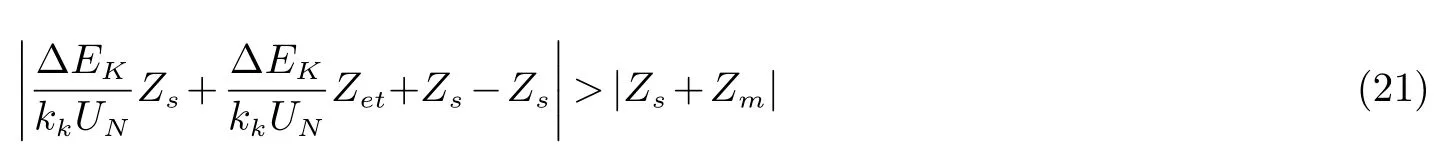
直流馈入下的系统阻抗等于直流系统等值工频变化量阻抗，因此直流馈入下的阻抗圆特性

忽略负荷的影响

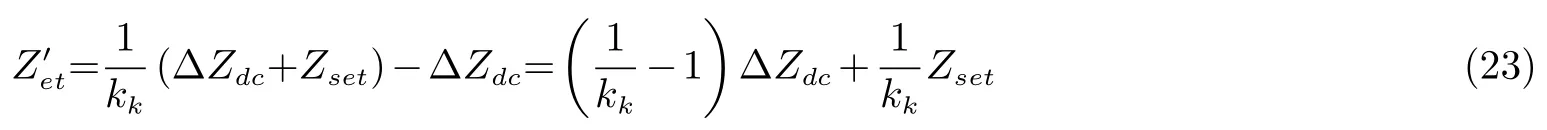
由式(22)、(23)可以看出直流馈入下的阻抗圆特性会受到∆Zdc和的影响，并且还会受到∆Zdc和kk的影响.因此，直流馈入造成∆Zdc的变化，会引起保护范围的减小.

3.1 直流系统工频变化量阻抗对保护范围的影响

交直流系统工频变化量距离保护阻抗圆特性，是以-∆Zdc为圆心，|∆Zdc+|为半径的圆.直流系统发生换相失败时，直流系统工频变化量阻抗呈容性，位于第三象限、第四象限，阻抗圆的圆心位于第二象限.而纯交流系统的系统阻抗呈感性，阻抗圆的圆心位于第三象限.因此，直流馈入会导致阻抗圆偏移，正方向保护范围减小.

由上述分析可知，过渡电阻越小，故障越严重，直流系统等值工频变化量阻抗幅值越大，正方向保护范围越小.阻抗圆特性如图6所示，A1为纯交流系统下的阻抗圆动作特性，A2为直流馈入下阻抗圆动作特性，A3为直流系统等值工频变化量阻抗幅值较小的阻抗圆动作特性.

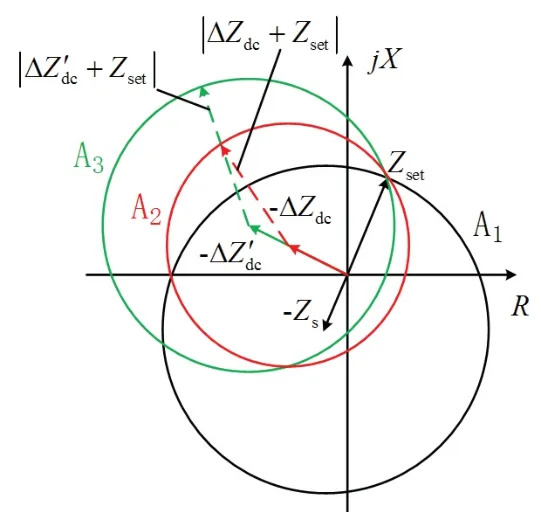
图6 直流馈入下工频变化量距离元件动作特性Fig 6 Operating characteristics of distance element based on the power-frequency variation in HVDC system

显然，直流馈入造成阻抗圆特性的圆心偏移，工频变化量距离保护正方向保护范围减小.

3.2 整定阻抗对保护范围的影响

3.2.1 可靠系数对整定阻抗的影响

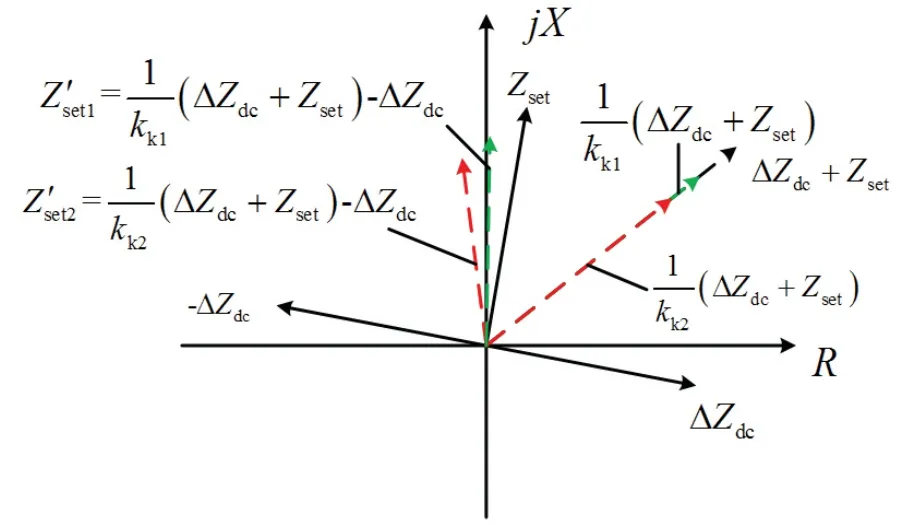
图7 整定阻抗随可靠系数变化向量图Fig 7 Schematic diagram of setting impedance changing with reliability coefficient

由图7可以看出，随着kk的增大，的幅值不断降低，且向第二象限趋近.由式(22)可得，工频变化量阻抗圆的半径会逐渐变小，导致正方向保护范围降低，当kk增大到一定程度后，正方向可能会失去保护范围.

3.2.2 直流系统等值阻抗对整定阻抗的影响

由上述分析可知，故障越严重，直流系统等值阻抗越大.当kk一定时，随着直流系统等值阻抗的增加，的幅值会不断增加，并且逐渐向第二象限转动，导致正方向保护范围减小，当故障严重到一定程度后，正方向会失去保护范围.随∆Zdc变化如图8所示.

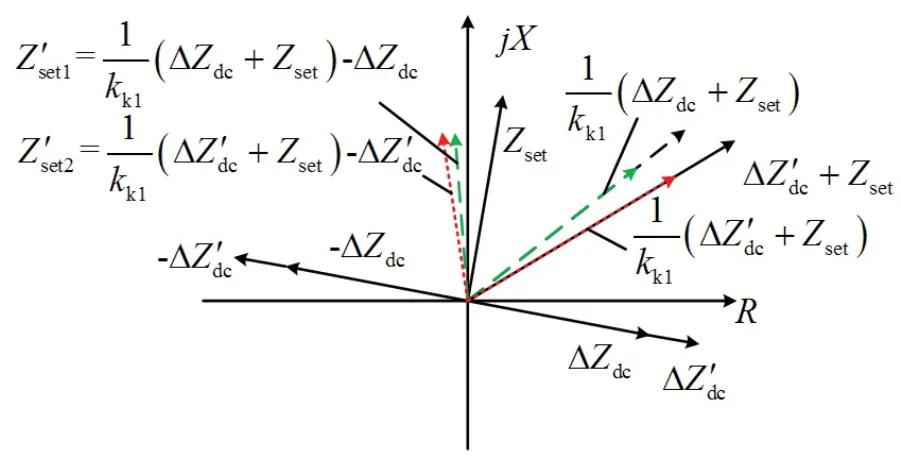
图8 整定阻抗随系统阻抗变化示意图Fig 8 Schematic diagram of setting impedance changing with system impedance

4 工频变化量距离保护改进策略

为解决直流馈入造成保护正方向范围减小的问题.提出工频变化量阻抗继电器与全阻抗继电器配合使用的方法.

全阻抗继电器的特性圆的圆心位于原点，正方向整定阻抗与反方向整定阻抗大小相等，Zset1=Zset2，动作区域如图9所示.

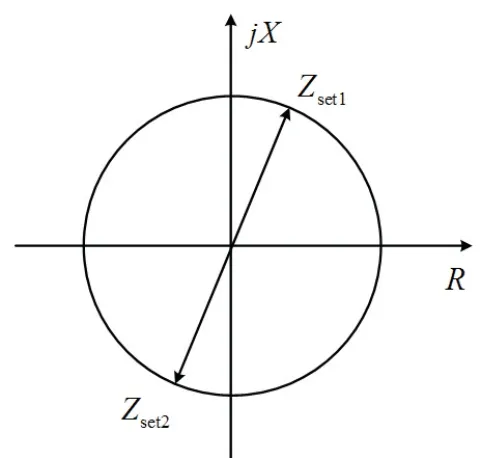
图9 全阻抗圆特性Fig 9 Operating characteristics of impedance relay

其动作特性为

全阻抗圆特性在各个方向上的动作阻抗都相同，正反方向故障下具有相同的保护区，不容易受到系统变化的影响，但本身不具有方向性，在双端电源系统中，应该与方向元件配合使用.而工频变化量阻抗继电器在正方向保护时快速可靠动作，而在反方向故障时，可靠不动作，因此可以作为方向元件使用.两种继电器取长补短，提出工频变化量阻抗继电器与全阻抗继电器采用或相互配合策略，配合方式如图10所示.

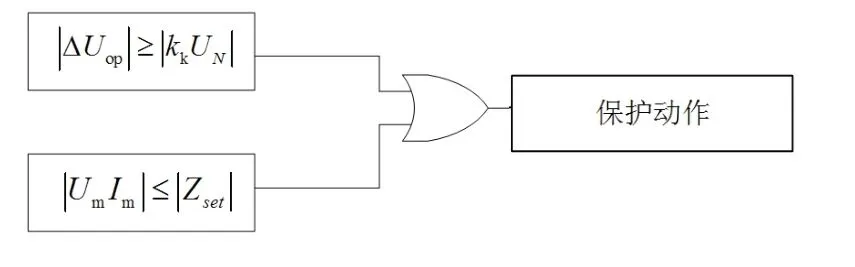
图10 工频变化量阻抗继电器与全阻抗继电配合Fig 10 Cooperation between power frequency variation impedance relay and impedance relay

工频变化量阻抗继电器仍采用固定门槛动作判据.纯交流系统和直流馈入下的阻抗圆如图11中A1、A2所示.全阻抗圆继电器动作范围如阻抗圆A3所示.全阻抗继电器以工频变化量阻抗继电器的初始整定阻抗为半径，以原点为圆心，内切与工频变化量正方向阻抗圆.

由图11可知，全阻抗继电器的阻抗圆特性与工频变化量阻抗继电器不同，其圆心位于原点处，因此，无论系统如何变化，均不改变其阻抗圆的位置.而全阻抗继电器阻抗圆的半径为整定阻抗，与保护安装处所测得电气量的变化无关.因此全阻抗继电器的动作特性不受直流馈入的影响.

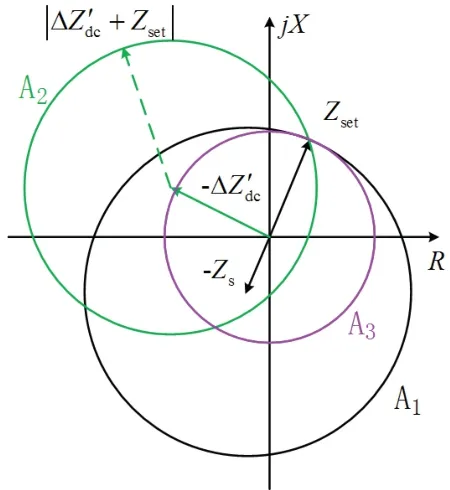
图11 两继电器配合动作特性Fig 11 Operating characteristics of two impedance relays

两继电器采用如图12所示方式进行配合动作.

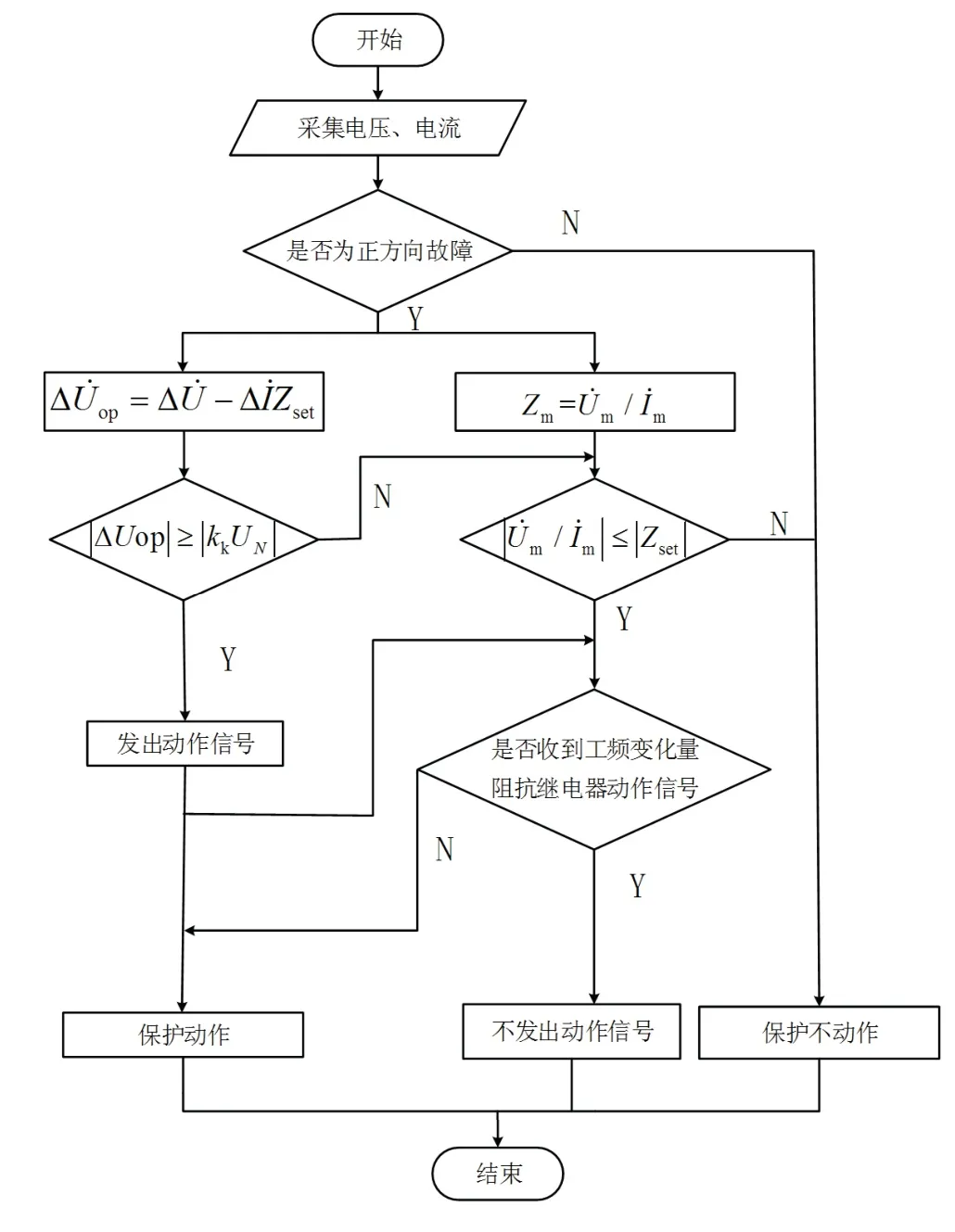
图12 工频变化量阻抗继电器与全阻抗继电器配合流程图Fig 12 Flow chart of cooperation between power frequency variation impedance relay and impedance relay

全阻抗继电器和工频变化量阻抗继电器协同工作.故障发生时刻，工频变化量阻抗继电器作为方向元件，对故障方向进行判断.当发生反方向故障时，发出信号闭锁两继电器，保护不动作.当发生正方向故障时，两个继电器同时工作，当满足工频变化量距离继电器动作特性时，发出动作信号，保护动作.全阻抗继电器在接受到工频变化量发出的动作信号后，闭锁继电器，不发出动作信号.

当不满足工频变化量阻抗继电器的动作特性时，工频变化量阻抗继电器将不发出动作信号，全阻抗继电器进行判定，如果满足动作条件且没有工频变化量阻抗继电器发出动作的信号，保护动作.若不满足动作条件，全阻抗继电器和工频变化量阻抗继电器均不发出动作信号，保护不动作.

5 仿真验证

5.1 直流馈入等值系统阻抗特性仿真验证

工频变化量阻抗继电器主要受∆Zdc的影响而导致正方向保护范围减小，基于PSCAD/EMTDC建立如图13所示模型.仿真模型采用GIGRE HVDC的标准测试系统，在其基础上搭建交直流混联系统仿真模型，不改变直流系统的情况下，调整了受端交流系统的容量.

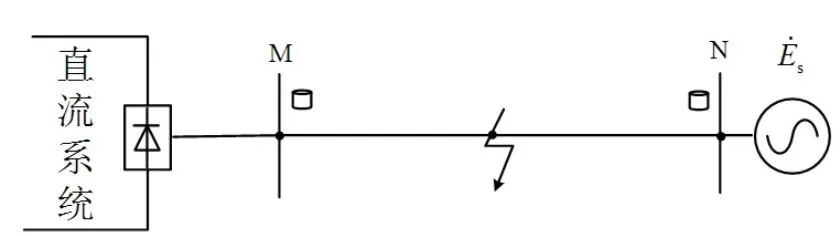
图13 HVDC仿真模型Fig 13 Simulation model of HVDC system

受过渡电阻影响，导致交流系统换流母线电压跌落情况不同，引起的直流系统换相失败情况不同.当受端系统SCR=2.5时，逆变侧交流母线电压发生A相经过渡电阻接地故障，分别经60 Ω、100 Ω、140 Ω接地，其中A相经140 Ω过渡电阻接地时，未发生换相失败，为发生换相失败的临界值；当受端系统SCR=5时，逆变侧交流母线电压发生A相经过渡电阻接地故障，分别经30 Ω、50 Ω、70 Ω接地，其中A相经70 Ω过渡电阻接地时，未发生换相失败，为发生换相失败的临界值，直流系统等值工频变化量阻抗仿真结果如图14、图15所示.

图14 不同故障下直流系统等值工频变化量阻抗相角Fig 14 DC-system impedance phase based on power-frequency variation under different commutation failure

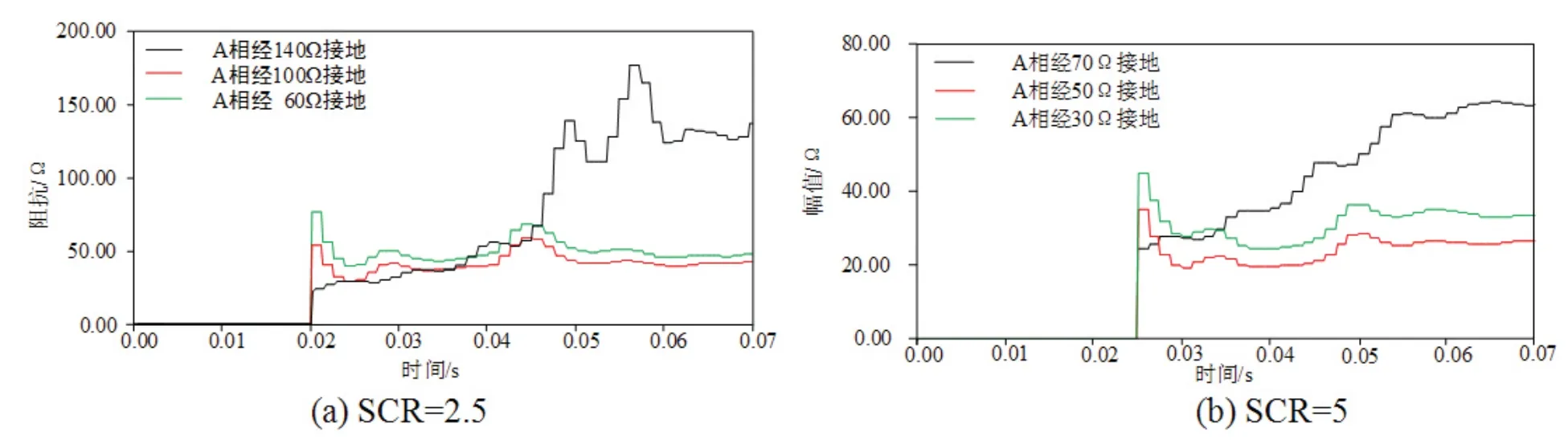
图15 不同故障下直流系统等值工频变化量阻抗幅值Fig 15 DC-system impedance amplitude based on power-frequency variation under different commutation failure

由图14、图15可知，直流系统等值工频变化量阻抗幅值在未发生换相失败时，持续上升.在换相失败的过程中，幅值先突增后减小.在一定过渡电阻下，直流系统等值工频变化量阻抗呈容性.

5.2 工频变化量距离保护改进策略仿真验证

设定系统参数，线路长度为50 km，线路正序参数如表1所示.

表1 线路参数Tab 1 Line parameters

采用式(1)和式(5)作为工频变化量阻抗元件的判据，可靠系数取1.1，保护范围为线路全长的80%.分别在线路出口保护安装处、线路全长40%、线路全长60%处发生AB两相短路，以上故障均为区内故障.工频变化量距离继电器判定的仿真结果如图16所示.

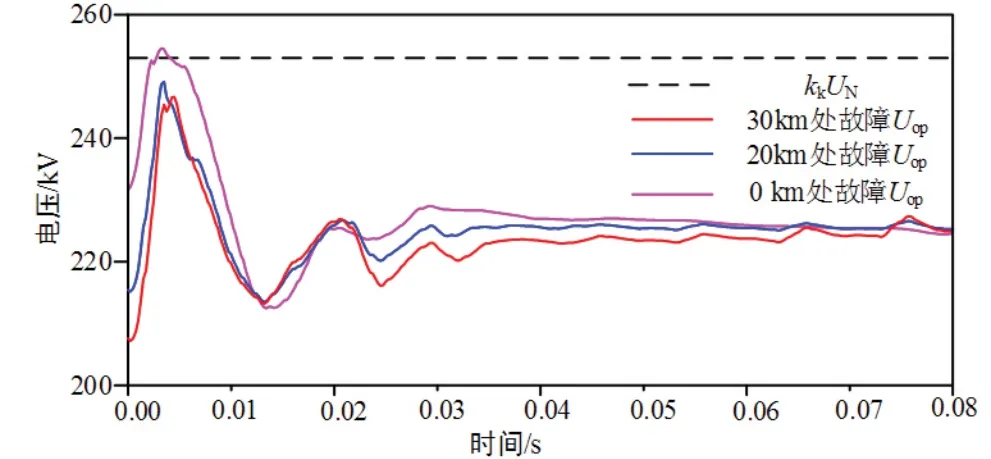
图16 区内故障工频变化量距离元件判定结果Fig 16 Response of power frequency variation impedance relay under internal faults

全阻抗继电器采用式(25)作为判据，仿真结果如图17所示.图中黑色的线为继电器测量电压，红色的线为保护末端整定电压.

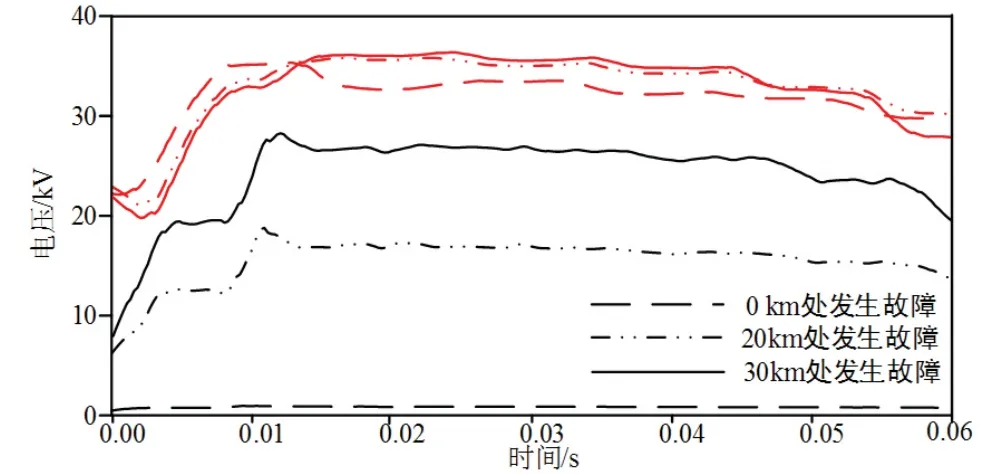
图17 区内故障全阻抗距离元件判定结果Fig 17 Response of impedance relay under internal fault

仿真结果表明，在线路出口处故障时，存在补偿电压幅值大于工频变化量阻抗继电器的整定电压幅值的现象.除此之外，工频变化量阻抗继电器的整定电压幅值均大于补偿电压幅值，因此，工频变化量距离保护不能正确发出动作信号.而全阻抗继电器的整定电压均大于继电器测量电压，因此可以正确发出动作信号，使保护正确动作.

在线路末端发生AB两相短路故障时，仿真结果如图18、图19所示.由图18、图19可知，在区外故障时，工频变化量阻抗继电器和全阻抗继电器均不会发出动作指令，保护不会动作，验证了所提改进措施的有效性.

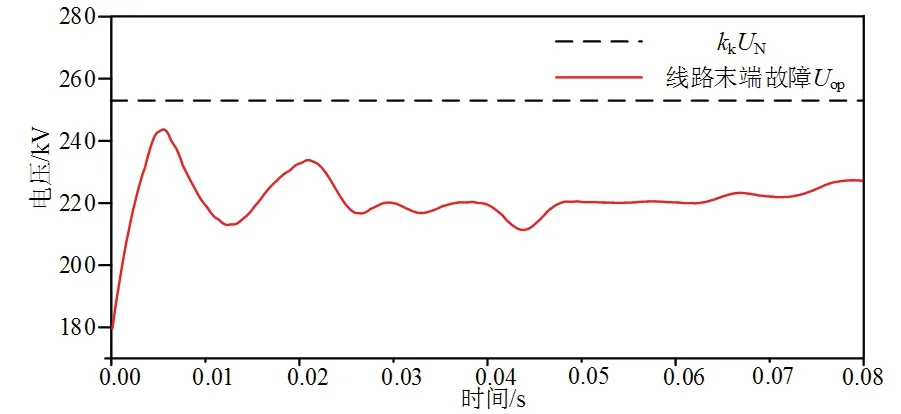
图18 区外故障工频故障分量距离元件判定结果Fig 18 Response of power frequency variation impedance relay under external faults

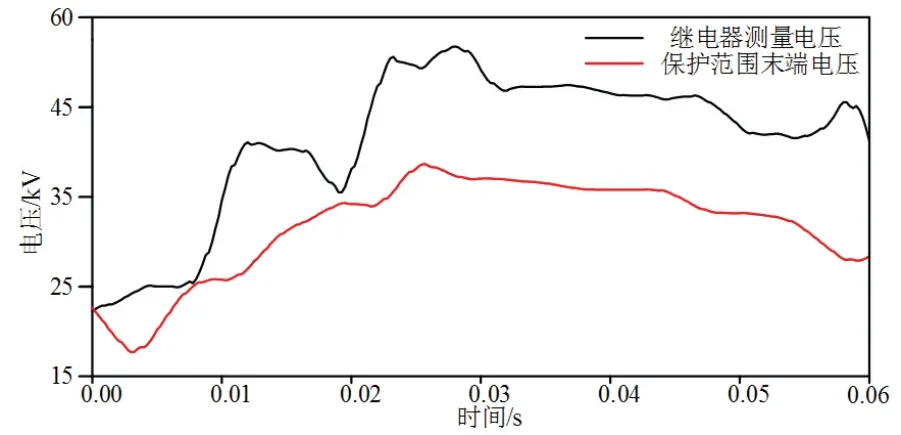
图19 区外故障全阻抗距离元件判定结果Fig 19 Response of impedance relay under external fault

6 结论

本文以CIGRE HVDC标准测试模型为例，研究了直流馈入对工频变化量距离保护的影响，并提出全阻抗继电器与工频变化量阻抗继电器相互配合的改进措施，得出如下结论.

(1) 直流馈入下直流侧等值工频变化量阻抗呈容性，处于第三或第四象限.使得阻抗圆圆心由纯交流时候的第三象限变为第二象限，使得阻抗圆由第一象限向第二象限移动，造成正方向保护范围的减小.可靠系数的增大会进一步造成正方向保护范围的减小.

(2) 全阻抗继电器与工频变化量阻抗继电器的配合使用，可以有效地防止由于直流馈入而造成工频变化量阻抗继电器区内拒动，同时兼顾保护的方向性和速动性.

(3) 全阻抗继电器虽能防止区内故障不正确动作，但由于其动作圆特性内切于工频变化量阻抗继电器，所以保护范围会略有减小.

本文通过仿真验证了上述结论的正确性和有效性，研究成果可为交直流混联系统其他类型保护提供思路，对于维护交直流混联系统安全稳定运行具有重要意义.