结合Harris和改进SIFT算法的遥感图像配准方法∗

王亚丽

(喀什大学 计算机科学与技术学院，新疆 喀什 844000)

0 引言

图像配准是将不同时间、不同视角或者是不同传感器条件下拍摄的同一场景的两幅或者多幅图像实现几何校准的过程[1−2].它是变化检测[3]、图像融合[4]和环境监测等领域中的基础处理.关于配准算法的研究大致可以分为两类，一类是基于灰度的方法，另一类是基于特征的方法[5].基于灰度的方法是通过全局灰度信息来进行相似性度量实现图像的配准，对图像尺度、角度和光照变化较敏感；基于特征的方法是通过提取图像中的重要稳定性特征并构造局部描述符来获得图像配准，该方法对灰度信息具有较强的鲁棒性，关键步骤是实现图像局部特征的识别、提取、描述和匹配.基于点特征的匹配主要有Harris算子[6]、SUSAN算子[7]、Harris-Affine算子[8]、ORB算子[9]等.Lowe提出尺度不变特征变换（Scale-Invariant Feature Transform，SIFT）算法[10]，该算法对图像的尺度缩放、角度旋转具有较好的不变性.Bay基于SIFT算法的思想提出SURF（Speeded Up Robust Features,SURF）算法[11]，SURF通过构造图像Hessian特征矩阵和Haar小波来提高特征提取速度，但是在尺度和旋转不变性上略不足于SIFT算法.近年来，基于特征的图像匹配方向上也有很多算法，例如，黄源等[12]给出相邻图像层次间不同的灰度量级设计的基于差分制约耦合三角网约束的图像匹配算法.岳娟等[13]提出具有近似仿射尺度不变特征的快速图像匹配算法等.这些算法多用于自然图像的配准中.

在遥感图像配准方面，Li等[14]在尺度不变特征变换（SIFT）算法的基础上联合尺度方向约束准则，提高匹配鲁棒性.Fan等[15]从空间关系出发，去除尺度空间中第一层特征点得到的初始匹配特征，使用多个局部邻域来提取描述子以增强其区别度.Dellinger提出的SAR-SIFT算法[16]，是针对SAR图像提出新的梯度计算方法改进SIFT算法.冷成财等提出基于尺度、方向和距离约束的改进SIFT配准方法（SODC-SIFT）[17].这些算法都是针对遥感图像配准鲁棒性不高，在尺度不变特征变换（SIFT）算法的基础上提出的改进算法.但是这些算法对于存在较大灰度差异的异源遥感图像来说配准仍然面临巨大的挑战.

本文提出结合Harris改进SIFT算法的遥感图像配准方法，在构建高斯尺度空间前求解遥感图像的一阶梯度图像，减少遥感图像间的灰度差异.然后基于一阶梯度的高斯尺度空间图像上提取Harris角点，并求SIFT描述符.最后用最近邻与次近邻比值法进行图像粗匹配，随机抽样一致性算法进一步精匹配，并求得仿射变换模型参数，完成遥感图像配准.

1 SIFT算法原理

由二维高斯函数和输入图像卷积生成尺度空间图像，定义高斯尺度空间图像为：

其中：I(x,y)表示原图像，G(x,y,σ)表示二维高斯函数，σ表示高斯函数标准差，也表示尺度空间的尺度因子.

通过求解相邻高斯尺度空间图像的差来求解高斯差分尺度空间（DOG），用作高斯拉普拉斯算子的近似.相应公式为：

其中：k是常量，表示相邻尺度空间的倍数，在SIFT算法中常取值为21/3.

尺度不变特征变换（SIFT）算法是在建立高斯差分尺度空间后，比较尺度空间中的26个点（上下两层各9个点和同层8个点），选择局部极值点作为候选关键点.用拟合三维二次函数精确候选特征点的位置与尺度，并且删除低对比度的候选特征点和不稳定的边缘响应点.

利用图像的梯度直方图，确定每个关键点的主方向.将梯度幅度与梯度方向定义为：

将坐标轴旋转为特征点的方向，旋转后以主方向为中心取16×16像素的领域，将其分成16个4×4的种子点，并计算每个种子点8个方向的向量，形成128维描述符.使用描述符上的最小欧式距离描述子进行相似性度量.

2 本文算法

结合Harris改进SIFT算法的遥感图像配准主要包括以下几个步骤：

（1）对参考图像与待配准图像求取一阶梯度图像；

（2）在一阶梯度图像上建立高斯尺度空间，不采取下采样操作；

（3）在建立的尺度空间图像上求Harris角点，使得Harris算子具备尺度不变性；

（4）对得到的Harris角点构建SIFT描述符；

（5）用最近邻与次近邻比值法对图像实现粗匹配；

（6）利用随机抽样一致性算法(RANdom Sample Consensus，RANSAC)[18]消除误匹配，并求得仿射变换模型参数，完成遥感图像配准.

2.1 遥感图像一阶梯度图像的确定

我们用Sobel算子与原图像卷积，得到图像一阶梯度幅值.一阶梯度幅值图像组与原图像组相比，图像灰度差异明显降低.如图1所示，图1（a）、图1（b）分别为原图像组的参考图像和待配准图像，图1（c）、图1（d）分别为一阶梯度图像的参考图像和待配准图像.

图1 原图像组与一阶梯度幅值图像组的对比图Fig 1 Comparison between the original image group and the first step amplitude image group

2.2 角点检测

对比原图像和一阶梯度图像，一阶梯度图像的角点更加明显，所以选择检测角点的方法来提取特征.Harris算子计算简单，只需要计算图像的一阶梯度和滤波.而且具有较好的抗噪性能，提取的特征点稳定、均匀而且合理，所以选择Harris角点检测方法.但Harris算子不具备尺度不变性，因而我们选择建立高斯尺度空间，将遥感图像的一阶梯度图像作为建立高斯尺度空间的输入图像.在这里需要说明，求得的尺度空间图像不需要进行下采样操作，选择在同一分辨率的高斯尺度空间图像上识别检测Harris角点.Harris函数定义为：

式中：u(X,σn)为多尺度Harris矩阵，tr(∗)和det(∗)分别表示方阵的迹和方阵行列式，D取0.04.多尺度Harris矩阵[19]定义为：

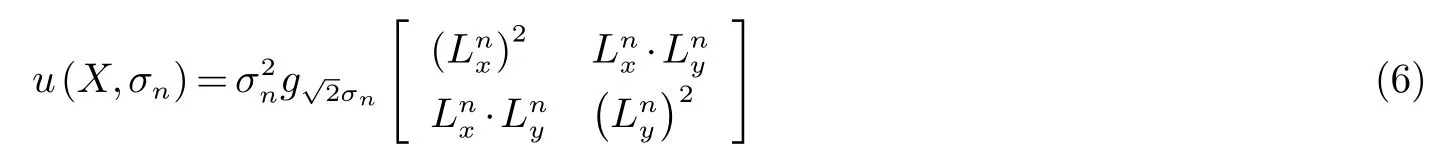
如果像素点X的Harris响应值（即R(X,σn)）大于8领域中任意像素点Harris响应值，同时大于Harris全局响应阈值Tth，那么该像素点X被认为是角点.

2.3 匹配优化

在初匹配阶段仍然采用基于欧式距离的最近邻与次近邻比值法，并且将其距离比阈值dratio设置为0.9，然后使用随机抽样一致性算法实现匹配优化.

3 实验仿真与分析

3.1 测试数据

本文对两组异源遥感图像进行实验测试来验证所提算法的有效性，这三组数据均来自于不同传感器，数据如图2所示，图2（a）、图2（b）为第一组测试数据集，图2（c）、图2（d）为第二组测试数据集，图2（e）、图2（f）为第三组测试数据集.数据参数如表1所示.

图2 测试数据组Fig 2 Test data set

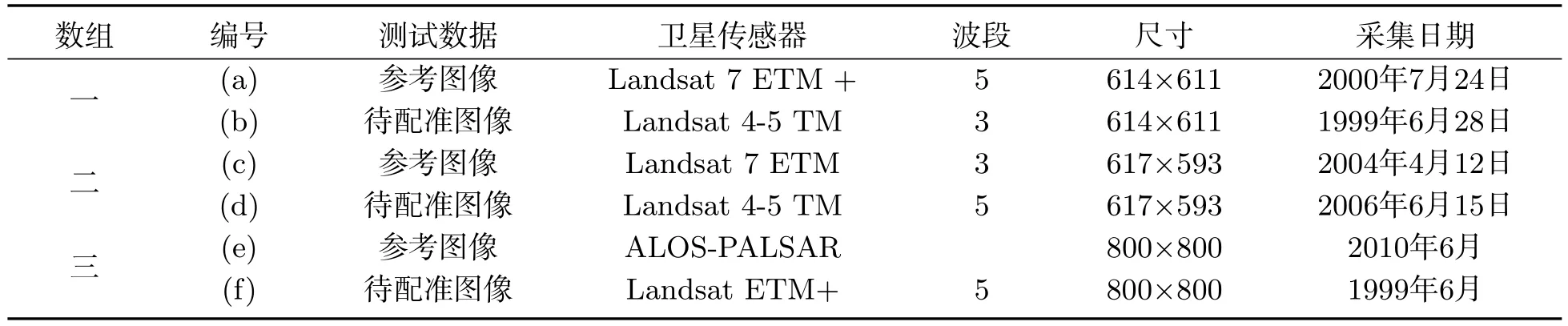
表1 测试数据信息表Tab 1 Test data information

3.2 实验结果与分析

本文采用均方根误差（RMSE）和正确匹配的关键点数量（N）来客观定量评价.均方根误差为：

其中：(xi,yi)和是第i个匹配点的坐标，为经仿射变换模型变换后的点坐标，N代表匹配点的总数.

为了验证本文算法的优势，与经典算法SIFT算法、SURF算法、SAR-SIFT算法对比，SIFT算法、SAR-SIFT算法是在MATLAB R2016a下采用Intel core 2.60 GHz处理器和8 GB物理内存，而SURF算法是使用C++语言实现的.对比结果如表2、表3和表4所示，*表示配准失败.

表2 第一组图像算法的比较Tab 2 Comparison of algorithms for the first group of images

表3 第二组图像算法的比较Tab 3 Comparison of algorithms for the second group of images

表4 第三组图像算法的比较Tab 4 Comparison of algorithms for the third group of images

从表2、表3和表4可以看到，如果遥感图像对之间存在特别大的灰度差异（接近相反）的时候，表2和表3反映SIFT算法，SURF算法以及SAR-SIFT算法都不能实现图像的成功配准，而本文算法针对灰度差异较大的问题给出解决方案，用图像的一阶梯度图像作为高斯尺度空间的输入图像，减少遥感图像对之间的灰度差异，对存在特别大灰度差异的遥感图像，在配准结果上可以实现成功配准.对灰度差异较大的遥感图像来说，由表4可知，在均方根误差和正确匹配点对数量上来看，配准精度明显提高.SAR-SIFT算法对第三组图像配准效果很好，因为我们的第三组图像的参考图像来自卫星ALOS-PALSAR，是SAR图像，而SAR-SIFT算法是针对SAR图像存在乘性噪声配准困难提出的算法，所以效果好.另外，本文算法使用的Harris算子时间较长，SURF算法使用C++，所以运行时间快.

图3给出本文算法的棋盘式配准图像，从配准图像的边缘以及区域都可以精确重叠，因此从直观方面可以判断配准结果是精确的，也再次验证所提出算法的准确性以及有效性.

图3 棋盘式配准图像Fig 3 Checkerboard registration image

4 总结

本文为了解决遥感图像配准中异源图像存在显著灰度差异带来的配准困难问题，提出了结合Harris改进SIFT算法的遥感图像配准方法.该方法用Sobel算子与原图像卷积求取图像的一阶梯度图像作为高斯尺度空间的输入图像；用Harris角点检测提取特征，图像的角点明显存在于一阶梯度图像上，同时高斯尺度空间可以赋予Harris算子尺度不变性；使用随机抽样一致性算法剔除误匹配对，求得仿射变换模型参数，完成遥感图像配准.实验结果表明，该方法有效克服遥感图像对之间显著灰度差异带来的配准困难问题，且配准精度较高.