分层双轴各向异性介质电磁传播矩阵计算
朱 逸, 李建周, 秦则芸, 刘祥威, 张生俊
(1. 西北工业大学电子信息学院, 陕西 西安 710129;2. 试验物理与计算数学重点实验室, 北京 100076)
0 引 言
各向异性介质在武器隐身领域越来越受到重视[1-2],其电磁传播特性受到国内外专家学者的普遍关注[3-4]。目前,实现电大尺寸目标的低可探测性主要依靠赋形技术和雷达吸波材料技术[5-6]。由于各向异性介质特殊的电磁特性,不仅能吸收雷达发射波,还能通过控制介质光轴使散射波能量集中于雷达非观测方向,进一步提升目标隐身性能[7-8],因此在目标雷达特性研究领域,各向异性介质涂覆目标电磁散射建模备受关注[9-10]。
目前对各向异性介质涂层的处理手段主要有两种,一种是等效阻抗模型方法,该方法将涂覆目标等效为各向异性阻抗目标[11-12],利用表面等效阻抗去处理介质涂层的电磁边界问题,此方法的好处在于不用分析涂覆目标的内部场,能够快速实现散射问题求解,但该方法作为一种等效算法,计算准确度不能得到保证,并且适用范围也存在一定限制。另一种方法是分层模型方法[13-16],将目标表面涂层直接看作单层或者多层各向异性介质的吸附,对其内部场进行分析,该方法的优点是与真实情况相符,计算结果更为准确,普遍适用于各种情形,但其机理研究更为复杂和困难。对于分层模型方法,Teitler等最先开始了分层各向异性介质的反射特性研究[17]。Guiwich等研究了多层各向异性球体中的平面波散射递推公式[18]。Graham等研究了各向同性介质和双轴各向异性介质分界面电磁波的反射与折射规律,指出了主轴和坐标系夹角改变时反射系数和透射系数会显著改变[19-20]。郑宏兴等通过广义传播矩阵方法,获得分层单轴各向异性介质的电磁传播矩阵,并给出了计算单轴各向异性介质反射和透射系数的解析表达式[21]。姚菁晶使用多模射线法得到了分层各向异性介质涂覆无限大金属平板的反射系数,能计算金属平板涂覆单层介质时的反射系数[22]。
本文选择了广义传播矩阵方法对分层各向异性介质的电磁传播特性进行研究,该方法属于分层模型方法,需要对介质内部场进行分析,推导过程比较复杂,但更贴近于实际情况,计算精度高。前人已有工作主要是使用该方法对分层单轴各向异性介质的电磁传播特性进行研究,对于分层双轴各向异性介质,并未对其进行具体的分析,在实际的求解过程中仍存在一定的问题。本文重点针对分层双轴各向异性介质电磁传播矩阵计算存在的问题进行了探讨,指出求解双轴各向异性介质的特征波时,耦合矩阵特征向量应满足的条件;给出了适用于各种介质的广义反射(透射)矩阵和通常意义反射(透射)矩阵之间的转换关系;分析了多层介质涂覆于金属表面时,反射系数矩阵的计算方法。相对于前人只针对某些介质结构或介质种类进行分析计算[23],本文算法可以适用于各种均匀涂覆的介质情况。按介质结构分可以计算:单层介质和多层介质、有金属衬底和无金属衬底;按介质种类分可以计算:各向同性介质和各向异性介质,各向异性介质中又包括单轴各向异性介质和双轴各向异性介质;因此具有更强的普适性。与此同时,还进一步将所得电磁传播矩阵与弹跳射线(shooting and bouncing ray,SBR)法相结合,获得各向异性介质涂覆目标的雷达散射截面(radar cross section,RCS),在目标雷达特性研究领域有着重要意义。
1 介质中的本征波
在各向异性介质中,存在两种不同波矢量的电磁波,称为Ⅰ型波和Ⅱ型波。其电磁场本构关系为D=ε0ε×E,B=μ0μH,相对介电常数ε和相对磁导率μ均为二阶张量。
设z轴垂直于介质分界面,由Maxwell旋度方程:
将旋度算子、电场和磁场分解为横向分量和纵向分量,经过推导得到横向场与介质参数之间的关系[23]
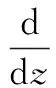
(1)
式中:V由电场和磁场的横向分量组成,V=[Ex,Ey,Hx,Hy]T,称为状态矢量;C为4×4阶矩阵,称为耦合矩阵,具体元素表达式如下:
C11=i(-kxεzx/εzz-kyμyz/μzz)
C12=i(-kxεzy/εzz+kxμyz/μzz)
C13=i(kxky/ωεzz+ωμyx-ωμyzμxz/μzz)
C21=i(-kyεzx/εzz-kyμxz/μzz)
C22=i(-kyεzx/εzz-kxμxz/μzz)
C24=i(-kxky/ωεzz-ωμyx+ωμxzμzy/μzz)
C31=i(-kxky/ωμzz+ωεyx-ωεyzεxz/εzz)
C33=i(-kxεyz/εzz-kxμzx/μzz)
C34=i(kxεyz/εzz-kxμzy/μzz)
C42=i(kxky/ωμzz+ωεyx-ωεxzεzy/εzz)
C43=i(kyεxz/εzz-kyμzx/μzz)
C44=i(-kxεxz/εzz-kyμzy/μzz)
式(1)的通解形式为
V(z)=AeiλzB
(2)
式中:λ为4×4阶对角阵,元素为C矩阵的特征值;A为C矩阵的4×4阶特征向量矩阵,列向量与特征值相对应;B为4×1阶矩阵,为待定系数,表示波的幅值。
如图1所示,区域0是各向同性介质,区域1是各向异性介质(包括单轴、双轴),假设电磁波从区域0入射。
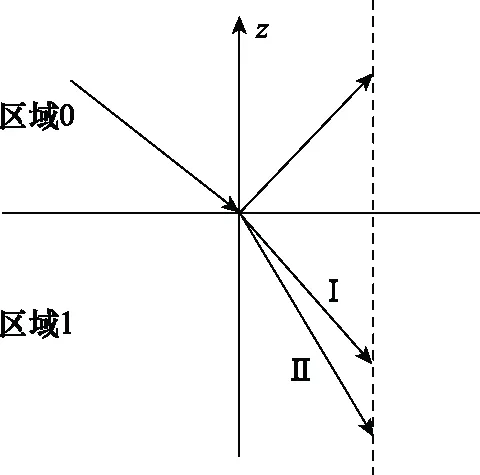
图1 各向异性介质界面Fig.1 Interface of anisotropic media
区域1中,存在Ⅰ型波和Ⅱ型波两种波,对应C矩阵的特征值形式为λ1=-λ3,λ2=-λ4,特征值大小分别与Ⅰ型波、Ⅱ型波的波矢量z轴方向分量相等,排列顺序对应Ⅰ型波和Ⅱ型波的上行波和下行波,A矩阵中的列向量与其一一对应。
区域0中,Ⅰ型波和Ⅱ型波退化成TE波和TM波,C矩阵特征值形式为λ1=λ2=-λ3=-λ4,不同大小的特征值分别对应一个二维特征向量空间。进行数值计算时,基底选取应满足TE波和TM波中电场和磁场x分量和y分量之间的关系。
当区域1中为单轴各向异性介质时,C矩阵可化简为反对角矩阵,各区域对应的特征向量矩阵形式为
(3)
此时,特征向量满足TE波和TM波条件。当区域1中为双轴各向异性介质时,各区域对应的特征向量矩阵形式为
(4)
为使区域0中特征向量满足TE波和TM波条件,区域0中特征向量矩阵的基底应满足:
(5)
式中:a0的上标代表区域0,文中所有上标都表示该参数处在的区域。进行数值计算时,应对A矩阵进行归一化处理,防止结果发散。
2 反射和透射系数计算
2.1 广义反射系数和透射系数
如图2所示的多层介质,区域0和区域n+1为自由空间,其余为各向异性介质。在两种介质的分界面上,Ⅰ型波和Ⅱ型波的入射均会产生Ⅰ型波和Ⅱ型波的反射和透射。
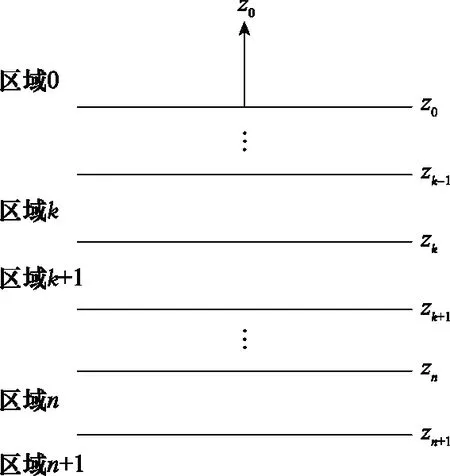
图2 分层各向异性介质Fig.2 Layered anisotropic media
平面波在介质内任意两点z和z′的传播特性可表示为
V(z)=Aeiλ(z-z′)A-1Aeiλz′B=P(z,z′)V(z′)
(6)
式中:P(z,z′)为广义传播矩阵。在第k层中:
Pk(z,z′)=Akeiλk(z-z′)(Ak)-1
(7)
根据界面处电场和磁场切向分量连续的边界条件,整个分层介质的传播矩阵为
(8)
为表示入射波与反射波透射波之间的关系,假定B1和B3是TE波广义振幅,B2和B4是TM波广义振幅,定义广义反射系数R和广义透射系数T分别为

(9)
在区域n+1中:
(10)
结合式(8)~式(10)得到整个分层介质的反射和透射系数关系式:
(11)
式中:I为2×2阶单位矩阵。由式(2)可求出各个区域的本征矩阵A,R和T便可由式(11)解出。
2.2 通常意义下反射系数和透射系数
得到广义反射和透射系数后,只能获得入射波和反射波透射波广义振幅之间的关系,还需将其转化为通常意义下的反射和透射系数
在区域0中,由式(2)得
等号右边的第1个矩阵的第1列和第3列代表TE波,第2列和第4列代表TM波。首先考虑TE波(TM波)入射时反射波为TE波(TM波)的同极化反射情况和TE波(TM波)入射时透射波为TE波(TM波)的同极化透射情况。二者的转换关系为
(12)
(13)
(14)
(15)
式中:⊥和∥分别表示垂直入射面和平行入射面;下标i、r、t分别表示入射、反射、透射。考虑TE波(TM波)入射时反射波为TM波(TE波)的交叉极化反射情况和TE波(TM波)入射时透射波为TM波(TE波)的交叉极化透射情况。二者的转换关系为
(16)
(17)
(18)
(19)
式中:η为区域0的本征波阻抗。当介质为单轴介质时,R12和R21等于0,不会产生交叉极化反射;双轴介质时,R12和R21不等于0,产生交叉极化反射。
2.3 金属表面各向异性涂层的反射系数
将多层各向异性介质涂覆于金属表面,即图2所示结构中区域n+1为金属。
区域0中,区域0的上行波是区域0下行波的反射加上区域1上行波的透射:
(20)
区域n中,区域n下行波是区域n-1下行波的透射加上区域n上行波的反射
(21)

将式(20)和式(21)相结合可得
(22)
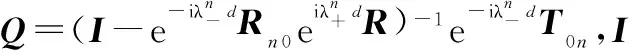
由式(22)得到包括金属衬底在内的总广义反射系数矩阵Γ,再利用式(12)~式(18)可求出通常意义下的反射系数。
3 算 例
本文算法适用于多种类型的介质涂覆结构,既可以实现介质涂层的角度特性分析,也可以实现介质涂层的频率特性分析。进行电磁传播矩阵计算时需要给出每层介质的厚度以及电磁参数矩阵ε和μ,可以是各向同性介质也可以是各向异性介质,并且要求各层介质都是均匀涂敷。现对不同结构各向异性介质的电磁传播矩阵进行计算,将所得结果与商业软件计算结果进行对比,验证该方法的正确性;并且将计算所得电磁传播矩阵运用于介质涂覆目标的电磁散射特性计算中。需要注意的是,在进行各向异性介质涂覆目标电磁散射特性计算时,需要给出各向异性介质的主轴涂覆方向。
3.1 单层双轴各向异性介质传播矩阵
对单层双轴各向异性介质的传播矩阵进行验证。设入射波频率为10 GHz,各向异性介质厚度为1 mm,电磁参数为

图3和图4分别给出了电磁波与介质表面水平方向入射角φ=0°和φ=30°时,反射系数模值和相位随电磁波垂直方向入射角θ的变化曲线。
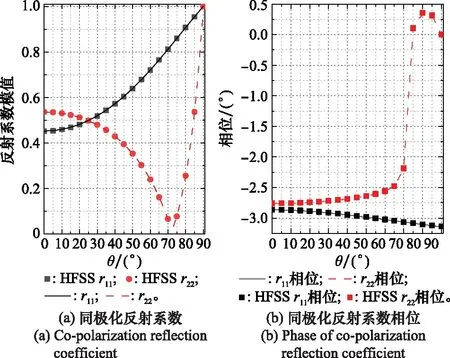
图3 反射系数(φ=0°)Fig.3 Reflection coefficient(φ=0°)
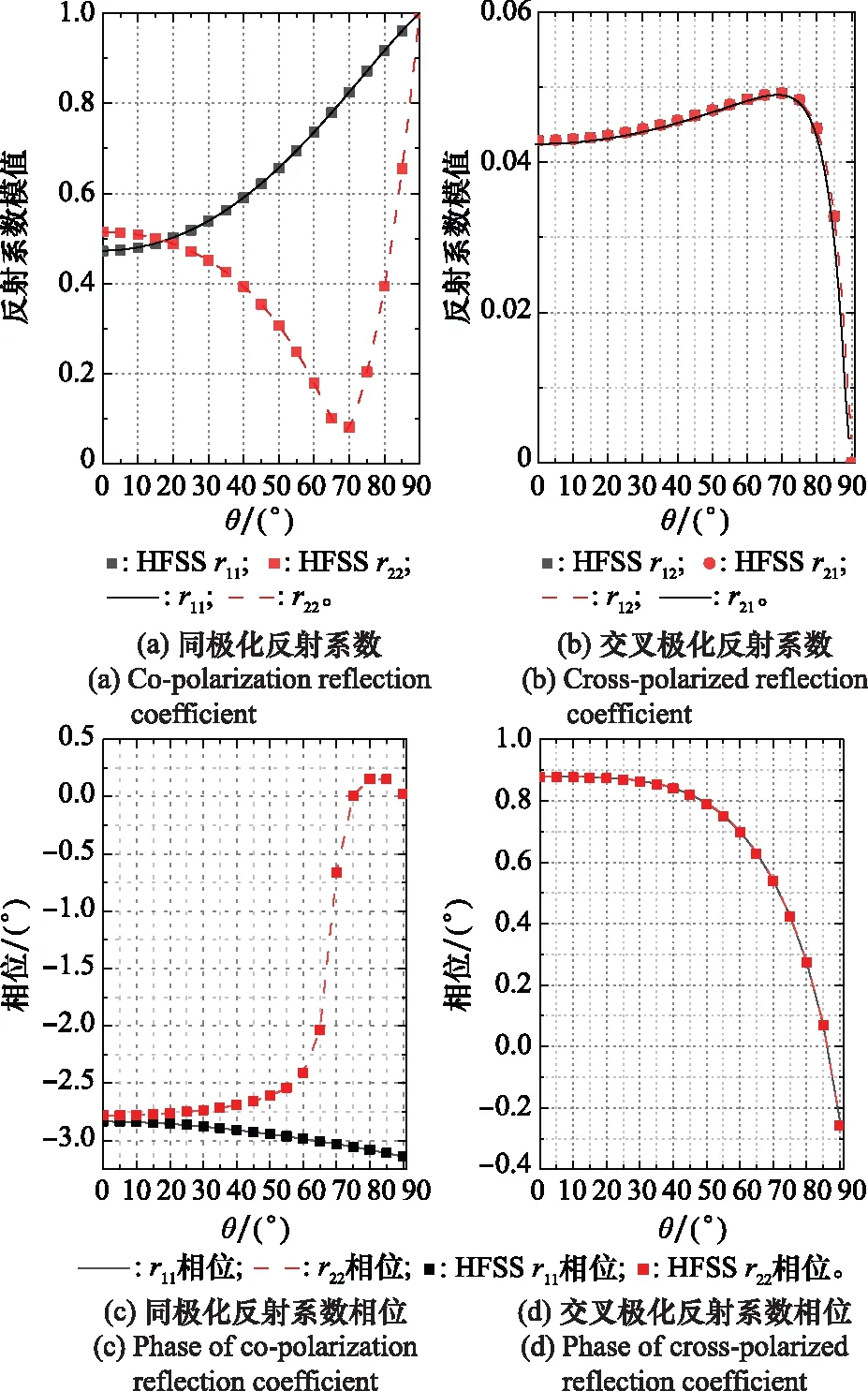
图4 反射系数(φ=30°)Fig.4 Reflection coefficient(φ=30°)
当φ=0°时,不存在交叉极化反射和透射;当φ=30°时,出现了明显的交叉极化现象。计算结果与HFSS仿真软件结果高度一致,证明了该方法的正确性。
3.2 金属衬底单层各向异性介质传播矩阵
在金属衬底上涂覆单层各向异性介质,介质厚度为1 mm,入射波频率为8.2 GHz,介质参数为

图5给出了反射系数模值和相位随电磁波垂直方向入射角θ的变化曲线。因为该介质为单轴各向异性介质,反射系数只随介质主轴和入射波之间的夹角变化。由介质参数可知该介质的主轴方向为z方向,故反射系数只受垂直方向入射角θ的影响,而与水平方向入射角φ无关,且不会产生交叉极化反射。
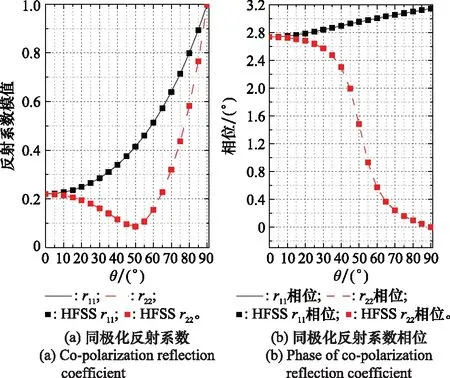
图5 反射系数Fig.5 Reflection coefficient
3.3 金属衬底多层各向异性介质传播矩阵
考虑金属衬底上涂覆多层各向异性介质的情况。这里选择3层均匀厚度的各向异性介质,介质厚度分别为1 mm、2 mm、0.5 mm,入射波频率为10 GHz,介质参数为
图6给出了电磁波与介质表面水平方向入射角φ=45°时,反射系数模值和相位随电磁波垂直方向入射角θ的变化曲线。图7给出了垂直方向入射角θ=0°时,交叉极化反射系数模值随电磁波水平方向入射角φ的变化曲线。
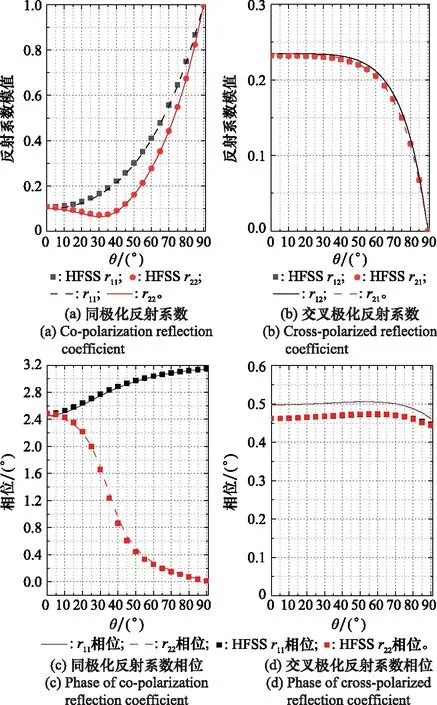
图6 分层各向异性介质反射系数Fig.6 Reflection coefficient of layered anisotropic media
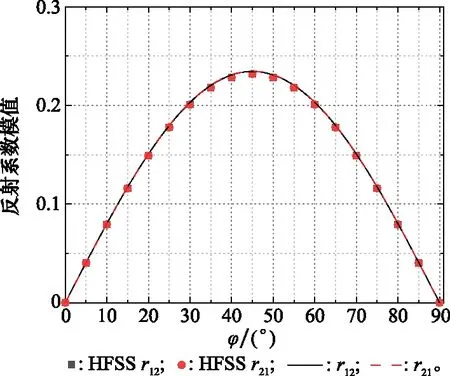
图7 交叉极化反射系数(θ=0°)Fig.7 Reflection coefficient of cross-polarized (θ=0°)
可以看出,交叉极化反射系数的大小随着水平方向入射角φ变化,φ=0°和φ=90°时不产生交叉极化,且交叉极化反射系数出现明显的峰值,材料的吸波性能会受到交叉极化反射的影响,因此对于各向异性材料涂覆目标性能优化问题应在一定程度上考虑材料的涂覆方向。
3.4 金属衬底单层各向异性介质频率特性分析
考虑入射波频率对各向异性介质电磁传播矩阵的影响,选取单轴各向异性介质,介质参数为
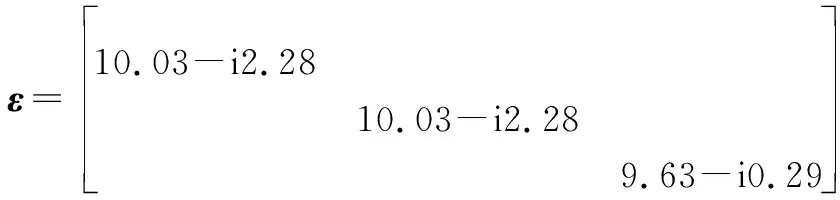
介质厚度为5 mm,涂覆于金属平板上,设置入射波角度分别为0°、30°、60°,反射系数模值随着频率变化的曲线如图8所示。
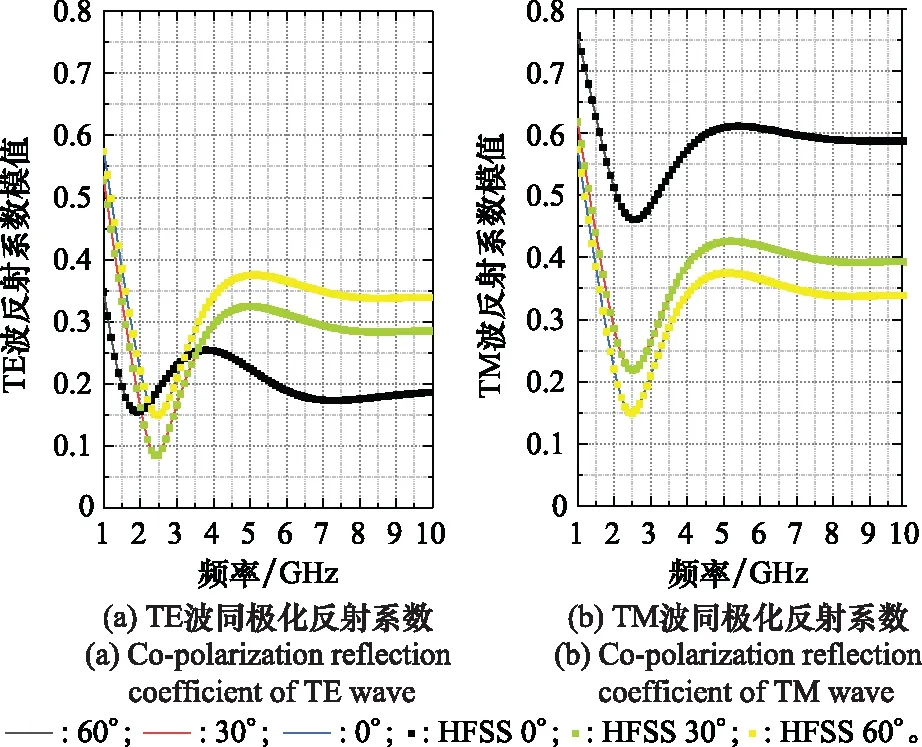
图8 反射系数模值频率变化曲线Fig.8 Frequency change curve of reflection coefficient modulus
计算结果与HFSS仿真结果保持一致,对比不同曲线可以看出,当入射角度从0°变到30°,反射系数模值变化明显,而从30°变到60°,反射系数模值变化不大,说明存在一定入射角度范围,入射角变化对反射系数模值影响较为明显。分析单条曲线随着频率的变化趋势,可以看出,反射系数模值大小明显存在一个最低点,说明这种介质在该频率处的吸波效果最好,同时在频率较低时,反射系数模值随着频率变化明显,当频率升高,反射系数模值基本保持不变。
3.5 涂覆目标电磁散射特性计算
将各向异性介质电磁传播矩阵与SBR算法相结合,从而获得各向异性介质涂覆目标的电磁散射特性[24-26]。
在实际的工程应用中,SBR法中的射线管路径追踪一直是个难题[27],而射线追踪的精度和效率决定了计算精度和效率。本文采用一种新型射线追踪方法,能准确地对非均匀有理B样条曲面模型进行射线追踪,相较传统的射线追踪方法更加高效和精确。对于各向异性介质涂覆目标的电磁散射特性计算,在射线追踪时,需根据射线管与涂覆材料主轴间的夹角,对每一个交点处的反射系数进行计算,用于射线管中心射线场强追踪,从而实现涂覆目标的电磁散射特性计算[28-30]。
3.5.1 各向同性介质涂覆导弹模型RCS计算
对导弹涂覆模型进行计算,导弹模型和尺寸如图9所示。
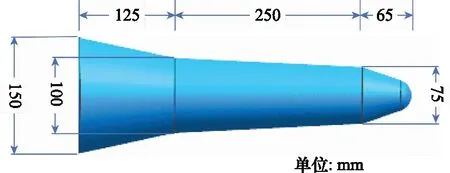
图9 导弹模型Fig.9 Missile model
计算了表面涂覆介质和表面不涂覆介质两种情况下的RCS。因为三维电磁仿真软件CST中不支持各向异性介质涂覆目标的RCS仿真,故选择各向同性有耗介质作为涂覆材料进行对比计算,其中介质参数为ε=3-i2,μ=1-i1,厚度为2 mm,入射波频率均为8.2 GHz。RCS结果如图10所示,表1中给出了RCS结果的均方根误差。

图10 导弹模型RCS结果Fig.10 RCS result of missile model

表1 RCS结果均方根误差
可以看出,在表面涂覆有耗介质之后,导弹RCS明显减小;并且在两种情况下,SBR算法结果与CST仿真结果保持一致,RCS结果均方根误差均小于3 dBsm,证明了该方法的准确性。
3.5.2 各向异性介质涂覆圆柱模型RCS计算
对圆柱体涂覆模型进行计算,入射波频率为10 GHz,圆柱的底面半径为10倍波长,高30倍波长,计算了各向异性介质涂覆时入射波水平极化和垂直极化两种情况,各向异性材料参数为εx=3-i4,εy=εz=7-i3,μ=1,各向异性介质涂覆方式如图11所示[6],其中实线箭头表示主轴方向。入射角φ=0°时,涂覆圆柱RCS随入射角θ变化的数值曲线如图12所示。所得结果与文献中的RCS结果基本一致。可以看出,对于各向异性涂覆,两种极化方式下目标RCS明显不同,这是因为不同极化情况下入射波电场方向和各向异性材料主轴间夹角不同,使射线管与目标交点处反射系数不同,导致不同极化情况下的RCS明显不同。
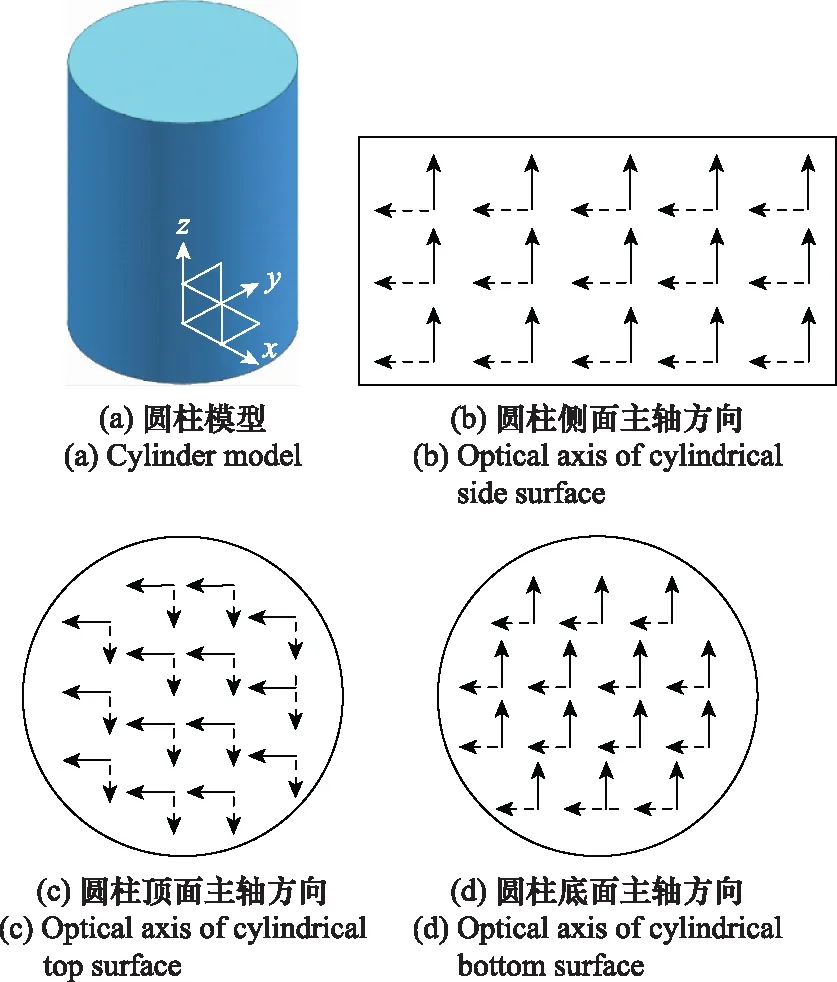
图11 圆柱涂覆模型Fig.11 Cylindrical coating model
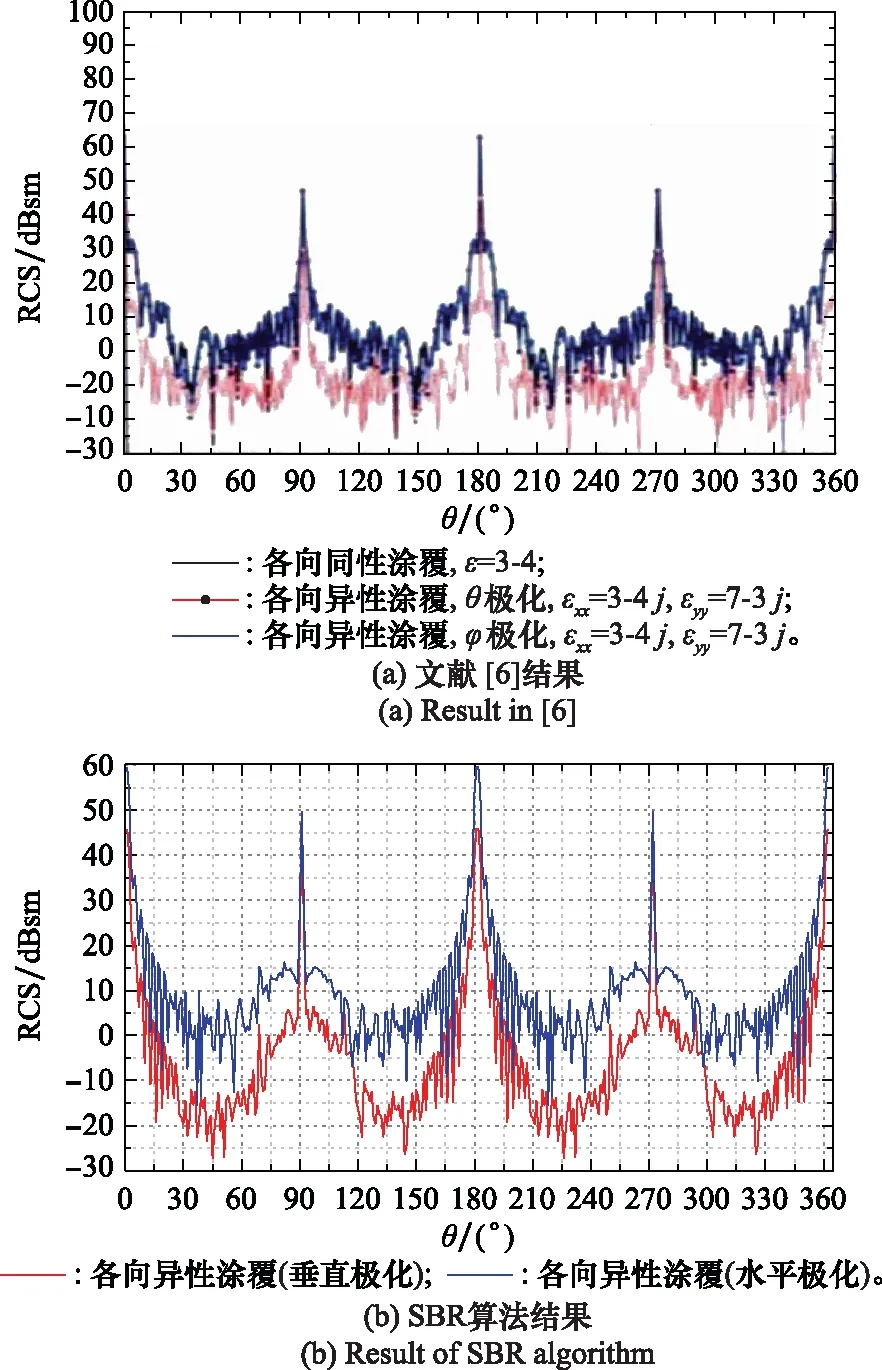
图12 圆柱涂覆模型RCS计算结果Fig.12 RCS calculation result of cylindrical coating model
4 结 论
本文在广义传播矩阵方法分析各向异性介质电磁传播特性的基础上,对分层双轴各向异性介质电磁传播矩阵计算问题进行了分析。将公式重新推导,指出了本征波求解时应该注意的问题,以及广义和通常意义下传播矩阵的转化关系,并对多层介质涂覆金属表面的情况进行了分析,使其能更普遍地运用于各种类型介质材料。将传播矩阵计算结果与新型弹跳射线法相结合,从而获得介质涂覆目标的电磁散射特性,所得结果还可以进一步运用于涂覆目标性能优化等问题,在目标雷达特性研究领域有着重大的应用前景。

