幅度相位误差条件下的互质阵列DOA估计方法

孙 兵, 阮怀林, 吴晨曦, 吴世龙, 钟 华

(国防科技大学电子对抗学院, 安徽 合肥 230037)

0 引 言

波达方向(direction of arrival, DOA)广泛应用于电子侦察、无线通信、导航等诸多领域[1-3]。在日益复杂的电磁环境中,会存在待测信源数大于阵元数的场景。目前,学者们针对均匀线性阵列提出了很多经典DOA估计算法,但均匀线阵的自由度受阵元个数限制,由N个阵元组成的均匀线阵(uniform line array, ULA)可达到的自由度为N-1,难以实现欠定条件下的DOA估计。为解决这一问题,文献[4]提出互质阵列结构模型,相较于传统均匀阵列,N阵元的互质阵列,其自由度可以达到Ο(N2)。互质阵列之所以具有这一优势是因为其差联合阵中拥有大小为Ο(N2)的虚拟均匀线阵部分。故该理论框架一经提出便受到了广泛的关注[5-8]。目前针对欠定条件下的互质阵列DOA估计算法主要包括空间平滑[9]、稀疏算法[10]、数组插值[11]等,这类基于差联合阵列的DOA估计方法均是基于理想的阵列模型提出的,但在实际应用中,幅相误差的存在难以避免,而互质阵列的差联合结构对于幅相误差非常敏感,这可能导致上述经典互质阵列DOA估计方法性能下降甚至测向失效。

文献[12]提出了一种正交匹配追踪算法,该方法将幅相误差作为附加误差矩阵来处理,尽管该方法可以应用于稀疏阵列,但并未充分利用稀疏阵列的自由度优势。文献[13]提出了一种基于匹配追踪的离格方法,该方法将非线性代价函数通过一阶泰勒级数近似,因而仅在误差较小时有效。文献[14]将误差校准问题转化为稀疏矩阵填充问题,并将非凸问题分解成两个凸子问题进行优化,但该方法仅适用于误差较小的情况。文献[15-17]提出了特征结构法,这类方法利用了信号子空间和噪声子空间之间的正交性,因此无法应用于欠定估计的互质阵列。文献[15]将存在幅相误差的阵元接收数据视为离群值,利用最大熵准则作约束条件以抑制幅相误差,但仅适用于均匀阵列。在文献[18]的基础上,文献[19-20]针对互质阵列分别提出了基于压缩感知和基于插值的互质阵列DOA估计方法,但假设前提是互质阵列中仅有极少数阵元存在幅相误差,其余阵元均是精确校准的,这一假设过于苛刻,在实际应用中具有很大的局限性。在文献[21-22]中,分别研究了非理想条件下的DOA估计,但假设前提是部分阵元完全失效并无法获取有用信息,对阵元作缺失置零处理,对于阵元存在幅相误差的非完全失效场景效果并不理想。因此,幅相误差条件下的互质阵列DOA估计问题没有得到有效解决。

针对上述问题,本文将4个已校正的辅助阵元加至原互质阵列,校正阵元位置按照互质阵列结构布置,增加校正阵元后的新阵列依然满足互质结构,可将新阵列视为两个均匀线阵构成,每个均匀线阵包含两个已校正阵元。在误差校正部分,受互质阵列子阵分解方法[23-25]启发,将互质阵列拆分为两个子均匀阵列进行误差估计。与传统均匀阵辅助阵元法[26-27]不同,该方法不要求辅助校正阵元数大于信源数,可适用于欠定DOA估计,并且仅需简单代数运算即可实现误差估计。在DOA估计部分,为了充分利用阵列自由度优势进行欠定DOA估计,在获得幅相误差后,将子阵幅相误差排序重组,对接收数据协方差矩阵进行误差补偿,并扩展为高维的Toeplitz矩阵,再利用矩阵填充理论进行空洞填充[28],恢复自由度,实现幅相误差条件下的互质阵列欠定DOA估计。

1 互质阵列幅相误差模型

图1给出了互质阵列结构示意图。互质阵列由两个线性均匀阵列组成,子阵1中包含N个阵元,间距为Md。子阵2中包含2M个阵元,间距为Nd,两个子阵共用第一个阵元组合成互质阵列,共2M+N-1个阵元。其中,M与N是两个互质的整数,d=λ/2为半波长。

图1 互质阵列示意图Fig.1 Illustration of coprime array

以第一个阵元为参考阵元,位置记为0,互质阵列阵元位置集合为

P={nMd, 0≤n≤N-1}∪{mNd, 0≤m≤2M-1}

(1)

假设有K个远场窄带信号分别入射至互质阵列,到达角θ=[θ1,θ2,…,θK],则阵列输出数据可表示为

X(t)=ΓAS(t)+N(t)

(2)

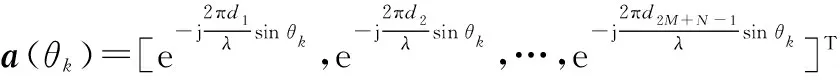
Γ=diag[γ1ejφ1,γ2ejφ2,…,γ2M+N -1ejφ2M+N -1]

(3)

式中：γi表示第i个阵元的幅度误差；φi表示第i个阵元的相位误差。

2 幅相误差条件下的互质阵列DOA估计方法

2.1 幅度相位误差估计

为校正互质阵列,将4个经过校正的辅助阵元添加至原始互质阵列,4个校正阵元位置如图2所示,图中增加校正阵元的新阵列依然满足互质结构。新阵列共2M+N+3个阵元,以第5个阵元作为参考阵元,位置记为0,新阵列阵元位置集合为

P1={nMd, -2≤n≤N-1}∪{mNd, -2≤m≤2M-1}

(4)

可将新阵列视为两组均匀线阵构成,每个均匀线阵均包含两个已校正阵元。第一组均匀线阵的阵元间距为Md,阵元数为N+2,第二组均匀线阵的阵元间距为Nd,阵元数为2M+2。两组均匀线阵共用图2中第5个阵元。

图2 增加校正阵元的阵列结构Fig.2 Array structure of adding correction array element

新阵列输出数据表示为

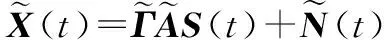
(5)

假设入射信号相互独立并且不相关,可以得到新阵列接收数据的协方差矩阵:

(6)

(7)

(8)

由此可得如下等式:

(9)

进一步可得

(10)

(11)

2.2 基于误差校正的互质阵列DOA估计

为了充分利用互质阵列自由度优势,在获得幅相误差后,对接收数据协方差矩阵直接进行误差补偿,并扩展为高维的Toeplitz矩阵,再利用矩阵填充理论进行空洞填充,提高自由度。

(12)

对于增加了校正阵元的新阵列,各阵元位置之差表示为

S={±(nMd-mNd)}∪{(niMd-njMd)}∪
{(miNd-mjNd)}

(13)

式中：-2≤n,ni,nj≤N-1;-2≤m,mi,mj≤2M-1。记dx为集合S中的元素,dx在集合S中出现的次数定义为权重系数ω(dx)。去除重复位置差得到虚拟阵元位置集合:

S0={-(2M+1)Nd,-2MNd,…,(2M+1)Nd}

(14)

实际应用中,快拍数有限,数据协方差矩阵R并非理想的Toeplitz矩阵,因而进行平均运算:

(15)

式中：Ri(dx)表示同一波程差对应的R中第i个协方差矩阵元素。

式(14)得到的差联合阵并非均匀阵列,其中存在空洞,传统方法仅利用连续虚拟阵元构成的均匀阵列,舍弃非均匀部分,为了提高虚拟阵元利用率,将协方差矩阵进行扩展得到一个数据缺失的高维协方差矩阵。将校正后的协方差矩阵R扩展成维数为(2MN+N+1)×(2MN+N+1)的Toeplitz矩阵RE,其元素为

(16)

式(16)扩展得到的RE某些位置元素为零。RE中的零元素与差联合阵的空洞是一一对应的关系。对RE中的零元素进行矩阵填充,即可实现对差联合阵空洞的填充。在一定约束条件下,由文献[29],矩阵填充问题可以用如下秩函数最小化模型来描述:

min rank(RV)
s.t.P·RE=P·RV

(17)

式中：RV表示待填充的目标矩阵；P表示投影映射矩阵。一旦差联合阵确定,则投影映射矩阵随之确定。具体表示为

(18)

由于秩函数是非凸的,所以式(17)是一个非确定性多项式难问题,而矩阵核范数是秩函数的近似,可以对模型(17)进行适当的凸松弛:

min ‖RV‖*
s.t.P·RE=P·RV

(19)

式中：‖RV‖*表示RV的核范数。核范数最小化问题直接求解效率不高,文献[30]提出的奇异值阈值算法(singular value thresholding algorithm, SVT)可以有效求解核范数凸优化问题,基于SVT算法,将式(19)转化为一个近似问题:

(20)

当μ→∞,式(20)的最优解逼近式(19)的解。因而通过选取一个较大的μ值,便可以实现凸松弛。对于式(20)所示的优化问题,SVT算法的求解如下:

(21)

式中:Y是过渡矩阵;δk为迭代步长,如果0<δk<2,则可以保证式(21)的矩阵填充问题收敛。但这一选择过于保守,收敛速度很慢,为简单起见,选择一个与迭代次数无关的常数δ=1.2n2/L,其中n为方阵RV的维数,L为采样数。Dμ为奇异值收缩算子,其定义为

(22)

式中:(σi-μ)+=max(0,σi-μ),σi表示Y的奇异值。

式(21)第k次迭代中,Yk-1的奇异值数目zk计算过程如下:

(23)

如果计算的奇异值已经小于μ,则说明zk选择正确。否则,需要重新定义一个增量h,增加zk直到奇异值低于μ。

在循环迭代时,如果满足:

(24)

则迭代停止,输出迭代结果RV。式中:ε是停止迭代阈值。

综上,幅度相位误差条件下的互质阵列DOA估计方法具体步骤如下。

步骤 4根据式(16)将R扩展成维数为(2MN+N+1)×(2MN+N+1)的Toeplitz矩阵RE。

步骤 5将RE的矩阵填充问题转化为式(17)秩函数最小化模型,再利用式(19)核范数最小化对式(17)进行凸松弛,最后基于奇异值阈值算法实现矩阵填充,得到目标矩阵RV。结合root-多重信号分类(multiple signal classification, MUSIC)算法进行DOA估计。

3 仿真实验

本节将进行仿真以验证所提算法的有效性。以M=3,N=5的互质阵列为例,存在幅相误差的阵元数为2M+N-1=10,增加4个辅助校正阵元,新阵列阵元数为14。仿真实验中各算法均采用14个阵元进行DOA估计。

3.1 可行性分析

将所提算法的性能与3种经典互质阵列DOA估计算法进行比较，包括空间平滑MUSIC(spatial smoothing-MUSIC, SS-MUSIC) 算法[9]，互质阵列最小绝对收缩和选择 (coprime array least absolute shrinkage and selection operator, CO-Lasso) 算法[10]和Interpolation算法[11]。设置MUSIC算法的角度搜索间隔为0.1°,CO-Lasso算法的预定义空间网格的采样间隔为0.1°。设有15个均匀分布于-42°至42°方向的远场窄带信号,信噪比SNR=10 dB,快拍数L=1 000。假设原互质阵列各阵元幅相误差为[0.4exp(-jπ/3),1.44 ·exp(jπ/4),0.52 exp(-jπ/3),1.45exp(j5π/6),0.6exp(jπ/4),1.73exp(jπ/3),0.51exp(-jπ/5),1.8exp(j3π/4),0.49·exp(-jπ/7),1.55 exp(jπ/3)]。4种算法的实验结果如图3所示。

由图3可得,存在幅相误差情况下,虽然设置了较高信噪比和快拍数,但3种经典互质阵列DOA估计算法效果均较差,这是因为互质阵列的差联合结构对于幅相误差非常敏感,因而导致3种经典方法的估计性能急剧下降。其中SS-MUSIC和Interpolation算法只能对少数信源实现DOA估计,CO-Lasso算法估计误差较大且出现伪峰。而本文算法可以对全部信源进行较准确的DOA估计。

3.2 分辨概率分析

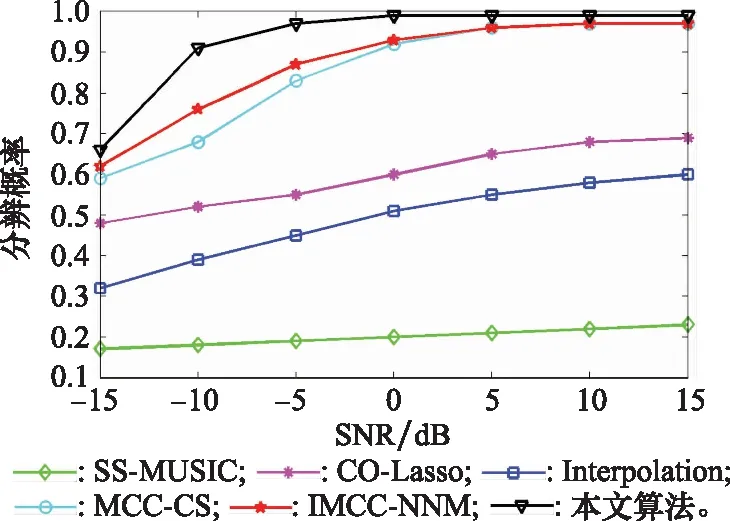
图4 分辨概率随SNR变化Fig.4 Resolution probability versus SNR

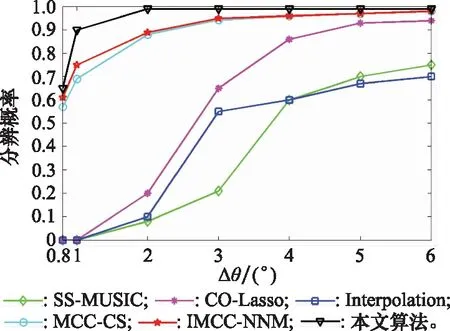
图5 分辨概率随角度间隔变化Fig.5 Resolution probability versus angular interval

由图4和图5可得，提高信噪比或增大角度间隔,各算法的角度分辨概率均随提高。在固定角度间隔为3°和快拍数为1 000的情况下,3种经典算法因为没有进行幅相误差校正,分辨概率较差。MCC-CS和IMCC-NNM算法随着信噪比进一步提高,能获得较高的分辨概率,但本文算法分辨性能更好,这是因为MCC-CS和IMCC-NNM算法的假设前提是互质阵列中仅有少数阵元存在幅相误差,其余阵元均是精确校准的,对于多数阵元存在幅相误差的条件下,性能下降,而本文算法没有这一限制。固定信噪比为5 dB和快拍数1 000的情况下,随着角度间隔的增大,各算法的分辨概率均显著增加,本文算法在角度间隔为2°时,角度分辨概率可接近100%,而各对比算法均无法达到。因而本文算法在不同信噪比和不同角度间隔情况下均具有明显的分辨优势。

3.3 估计精度分析

考虑两个信源的到达角分别为-10°,20°。图6实验中,对6种算法分别进行300次蒙特卡罗实验。快拍数设置为1 000,研究信噪比变化对DOA估计均方根误差的影响。图7实验中,对6种算法分别进行300次蒙特卡罗实验。信噪比设置为10 dB,研究快拍数变化对DOA估计均方根误差的影响。阵元幅相误差设置与第3.2节中相同。

图6 2信源RMSE随SNR变化Fig.6 RMSE versus SNR for 2 sources

图7 2信源RMSE随快拍数变化Fig.7 RMSE versus the number of snapshots for 2 sources

由图6和图7可得，相同条件下,提高信噪比或增加快拍数,6种算法的角度估计精度均有所提高。在较高信噪比和快拍数条件下,3种未校正算法估计精度较低,而MCC-CS、IMCC-NNM和本文算法均能获得较好的估计精度,且本文算法精度更高。

进一步比较欠定DOA估计条件下的各算法估计精度,假设16个信源均匀分布于-42°至48°。其他参数不变。图8为信噪比变化对DOA估计均方根误差的影响。图9为快拍数变化对DOA估计均方根误差的影响。

图8 16信源RMSE随SNR变化Fig.8 RMSE versus SNR for 16 sources

图9 16信源RMSE随快拍数变化Fig.9 RMSE versus the number of snapshots for 16 sources

由图8和图9可知，欠定DOA估计条件下,3种未校正的经典算法误差较大,基本失效。本文算法相比于MCC-CS和IMCC-NNM算法，能获得更高的估计精度。

4 结 论

考虑目前互质阵列DOA估计算法一般建立在阵列模型理想的条件下,若阵列存在幅相误差,现有算法性能下降甚至测向失效。本文提出一种基于校正阵元的互质阵列DOA估计方法。该方法将互质阵列接收数据分解为两个子阵数据,增加辅助校正阵元进行幅相误差估计,然后对接收数据协方差矩阵进行误差补偿,最后对补偿后的协方差矩阵进行扩展和空洞填充。本文方法有效恢复了幅相误差条件下的互质阵列DOA估计性能,提高了估计精度。