面向群体共识的三阶段犹豫模糊型信息融合方法研究

陶希闻, 江文奇

(1. 南京理工大学经济管理学院, 江苏 南京 210094; 2. 江苏产业集群决策咨询研究基地, 江苏 南京 210094)

0 引 言

群体决策中,个体决策者知识结构、认知逻辑等方面的差异最终体现为决策结果的分歧和冲突。面向群体共识需求而集结不同知识和偏好的个体决策者评价值,可以提高决策方案综合评价结果的有效性和应用价值[1]。通常,群体共识构建过程需充分考虑个体决策者原始意见,个体评估一致性检验、群体信息集结和群体共识改进是构建群体共识的重要内容[2]。

个体评价值的传递性特征是度量一致性水平的重要工具[3],文献[4-5]使用规划模型识别并改进个体评价的一致性;文献[6]提出了一致性识别和基于局部调整策略的一致性改进方法;文献[7]面向群体共识需求设计了一致性控制策略。现有方法对一致性调整幅度考虑不足,易扭曲原始评价信息。在群体偏好集结方面,集结效果的差异影响着群体决策效率和群体共识改进过程。文献[8]考察不同集结方式对群体共识度的影响,提出了基于有序集结算子(ordered weighted averaging,OWA)算子的集结模型;文献[9]利用决策者自信程度集结模糊偏好关系;文献[10]使用Choquet积分将评价值交互关系转换为决策者的权重信息并实施集结;文献[11]提出了诱导OWA(induced OWA, IOWA)算子,其中内生决策者权重由诱导值确定[12]。文献[13-15]分别以一致性水平、信息熵和相似度为诱导值,使用IOWA算子集结群体偏好,但群体偏好的共识程度可能无法满足需求。

群体共识改进过程会造成原始信息的损失,增加共识成本。线性加权方法通过个体评价与群体评价的线性加权更新个体评价,以提升群体偏好的接近程度。文献[16]采用局部信息反馈策略提升群体共识度;文献[17]考虑决策者合作意愿的差异性,以最大和谐度为目标提出个性化线性加权调整策略;文献[18]考察局部反馈策略中动态共识度阈值的确定方法。线性加权方法忽视了对调整幅度的控制,而且难以避免相同位置的重复调整。最小调整方法运用数学规划模型减少共识构建的偏好调整幅度。文献[19]考察了调整距离、评价值数量以及决策者数量对共识构建效率的影响;文献[20]基于模糊偏好关系设计了多阶段共识调整模型,忽视了对集结权重的优化。惩罚权重方法根据决策者合作程度更新其集结权重。文献[21]提出群体共识改进双重反馈机制;文献[22-24]针对决策者非合作行为动态调整群体偏好集结权重。惩罚权重方法不改变个体偏好,群体共识优化幅度比较有限。

总体上看,现有关于群体共识集结与优化的研究已经取得一定成果。但是对于模糊偏好关系群体共识构建模型的研究还不够充分:① 当决策者使用模糊偏好关系表达评价信息时,现有研究未对个体一致性水平进行甄别与调整,可能导致决策结果自相矛盾的情况;② 现有研究弱化了群体偏好集结方法的重要性,导致群体偏好集结的共识度较低,增加了共识调整的难度;③ 共识调整过程缺乏清晰的调整方向与步长,不仅会损失较多原始信息还会降低评价信息的一致性水平。为了描述实际决策过程中决策者在多个评价值之间犹豫不决的情况,本文以犹豫模糊偏好关系(hesitant fuzzy preference relations, HFPR)为研究背景[25-30],构建了面向群体共识的偏好关系信息融合模型,首先对决策个体的一致性水平进行甄别与调整,提升信息融合的可靠性与逻辑性;继而在最大群体共识度与最小共识调整距离的驱动下,运用贴进度诱导的有序集结算子集结群体偏好,并引入集结权重优化模型和弹性偏差算子依次调整群体偏好与个体偏好,在实现群体共识时兼顾原始评价信息保留,为实现高水平群体决策绩效提供理论指导。

1 犹豫模糊偏好关系基本概念

定义 1[27]设X是一给定论域,集合E={|x∈X}称为X上的犹豫模糊集(hesitant fuzzy set, HFS)其中,hE(x)是由区间[0,1]上若干个数值构成的集合,表示元素x属于集合X的若干种可能隶属度,简便起见,将hE(x)={γl|l=1,2,…,#hE(x)}称为犹豫模糊元(hesitant fuzzy element, HFE)[28],其中#hE(x)为犹豫模糊元hE(x)内元素个数。

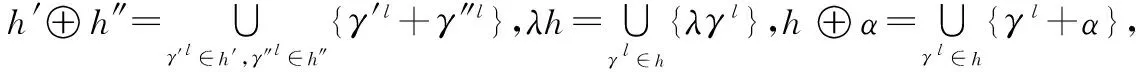
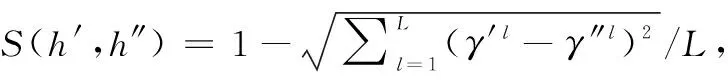
定义 5[29]诱导犹豫模糊有序加权算子(induced hesi-tant fuzzy OWA, IHFOWA)为Ωn→Ω的映射:

IHFOWAw([u1,h1],[u2,h2],…,[ut,ht])=

(1)

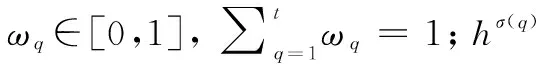
2 HFPR一致性检验与调整

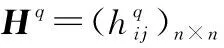
(1) HFPR一致性检验

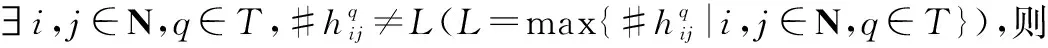
(2)

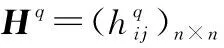
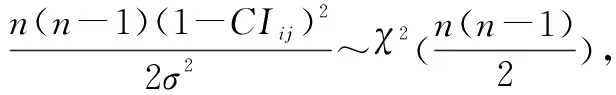
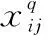
(2) HFPR一致性调整元素识别

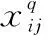
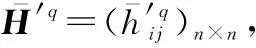
(3)

(3) HFPR一致性调整模型设计

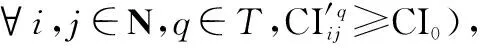
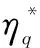
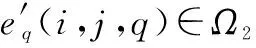
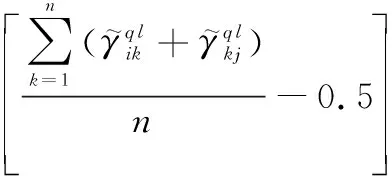
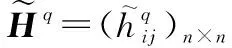
上述过程可以修正个体决策者自身的冲突判断,提升其判断的一致性水平,为群体信息集结奠定了良好基础。

3 HFPR群体信息集结模型研究

个体模糊偏好关系矩阵的一致性检验与调整是群体集结的基础,而构建高水平的群体共识需要确保群体集结结果的有效性。

(1) HFPR群体偏好集结

基于任一决策者与其他决策者的相似度越高则在群体意见中越重要的认知[15],将任一决策者与其他决策者相似度的均值定义为该决策者的贴进度,即

(4)

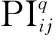
(5)

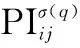
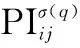
(6)

(7)

(2) 群体共识度阈值设定

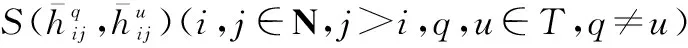
(8)

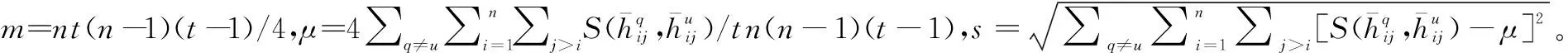
(9)

使用分位点Uα作为群体阈值GCI0=Uα。

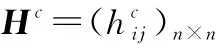
4 群体共识调整模型研究

本部分设计了融合集结权重优化和最小调整距离的共识改进模型。只有当集结权重优化难以实现群体共识要求时,才引入弹性偏差算子,以最小调整距离为目标对个体偏好进行调整。

(1) 群体偏好集结权重调整设计

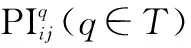
于是,其规划模型3可以表示为

(2) 个体偏好调整模型设计

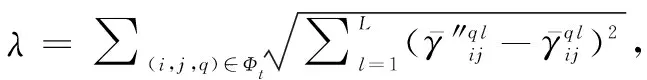
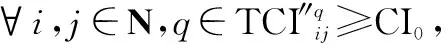
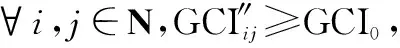
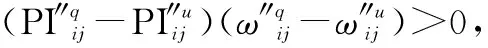
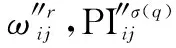
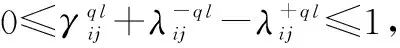
定理 1模型4至少有一个解。

证:由于Φ2⊂Φ3,则证明模型4有解,即证明t=3时,模型有解。

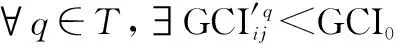
5 三阶段HFPR信息融合步骤

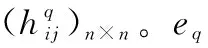
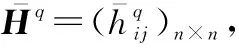
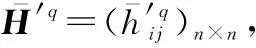
步骤 4利用式(8)和式(9)确定阈值GCI0=Uα;

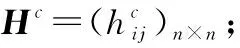
步骤 7计算群体共识度。若∀i,j∈N,GCIij>GCI0,转入步骤10,否则转入步骤8;

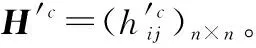
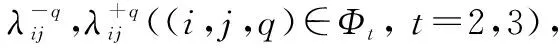
步骤 10形成群体共识,输出群体偏好。

上述技术路线可以描述为如图1所示。

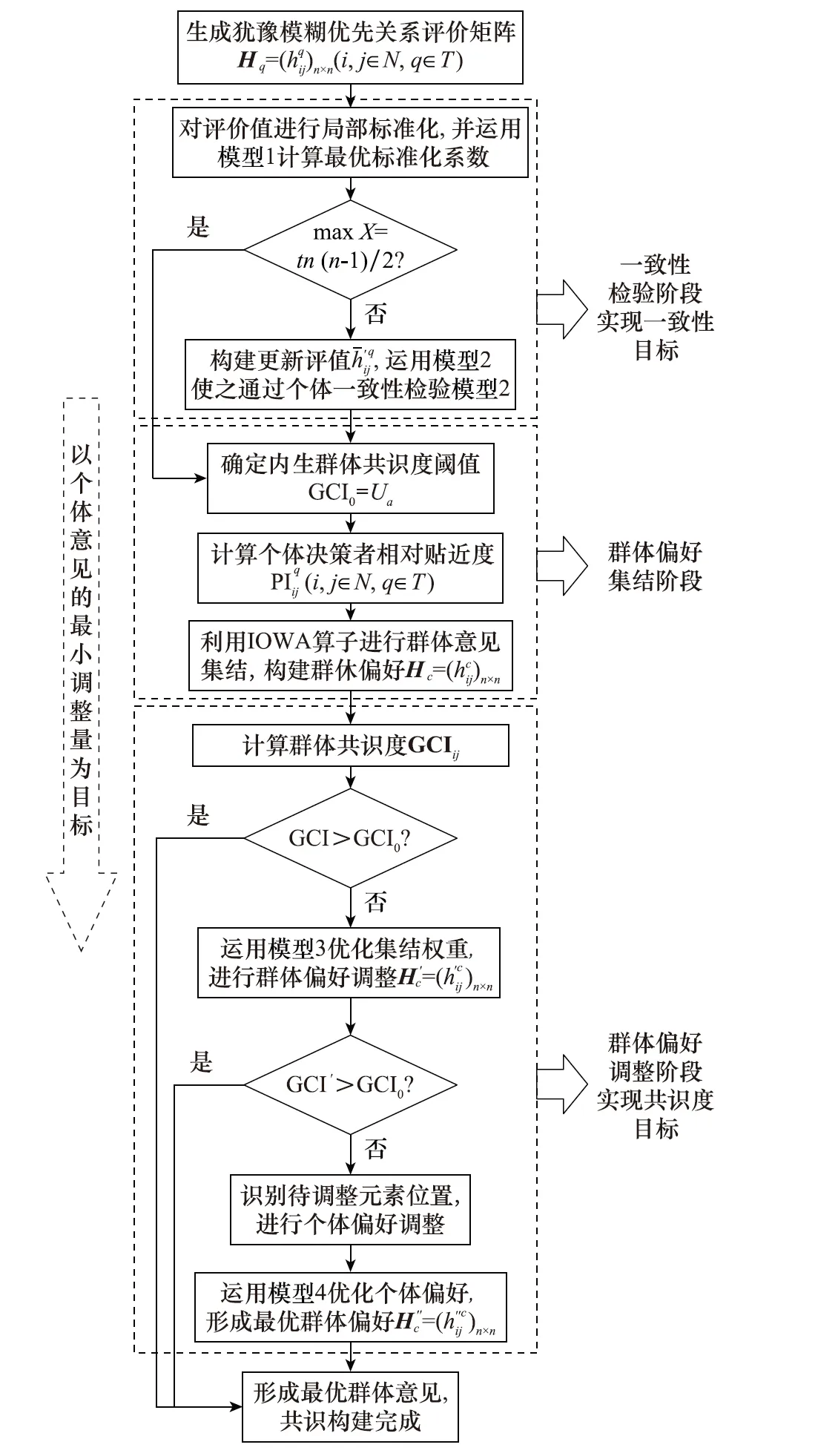
图1 HFPR信息融合步骤Fig.1 HFPR information fusion steps

6 算例研究与对比分析

(1) 算例研究

某公司评价其产品某重要部件的4个供应商{x1,x2,x3,x4},4位来自不同领域且经验丰富的专家{e1,e2,e3,e4}实施评估,各个专家使用犹豫模糊偏好关系比较4个供应商。

算例 1

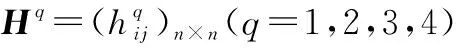
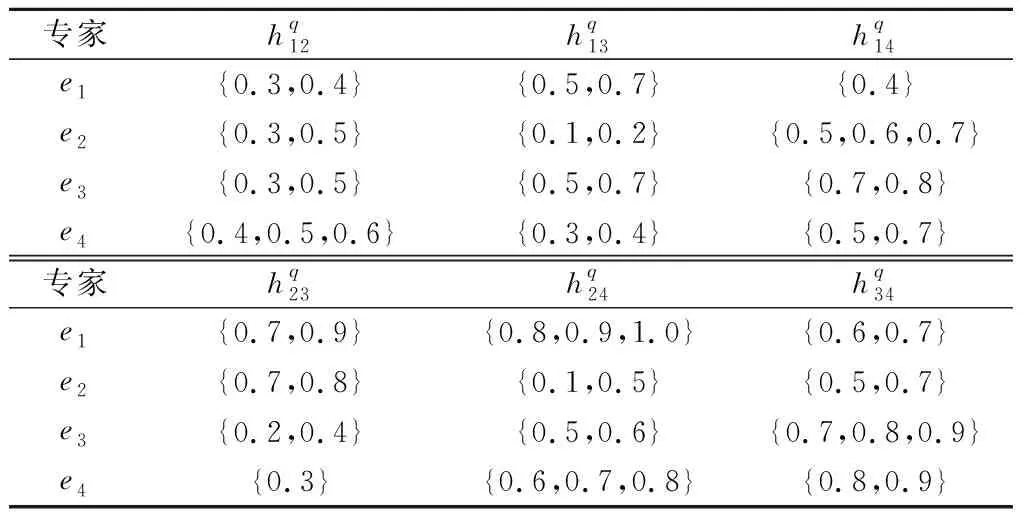
表1 决策群体HFPR评价值

步骤 2令σ0=0.1,α=0.1,则个体一致性阈值为CI0=0.89,使用模型1求解最优标准化系数如下。

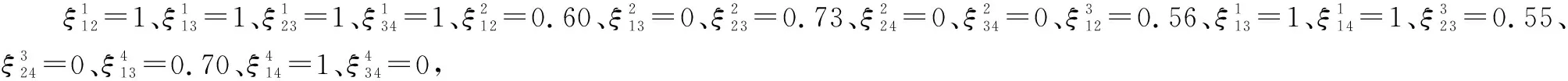
表2 决策者评价值的一致性水平

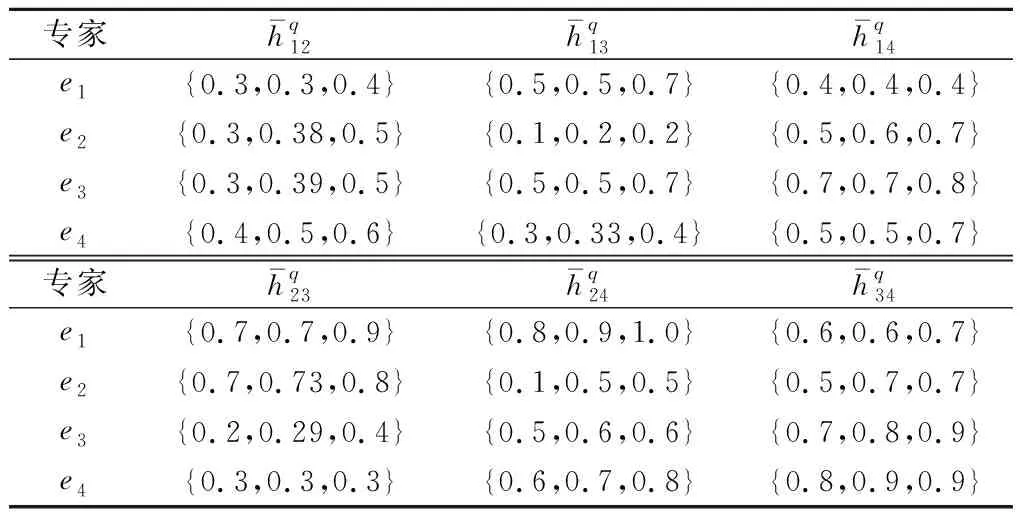
表3 决策群体标准化HFPR评价值

由于maxX=21≤24,则转入步骤3;

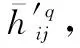
则更新评价值为

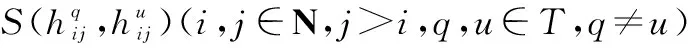
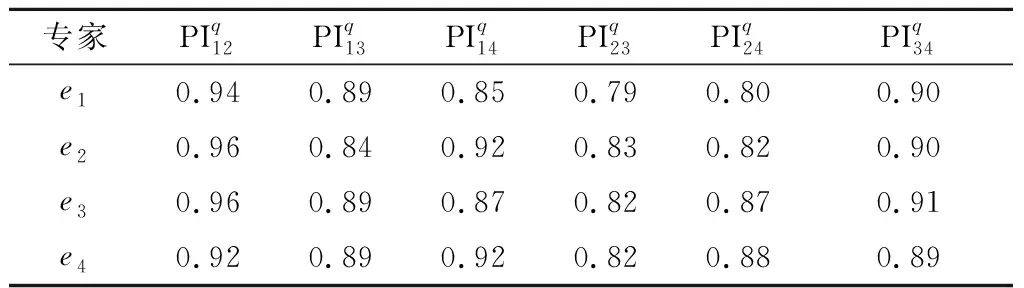
表4 决策者贴进度

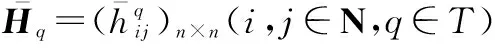
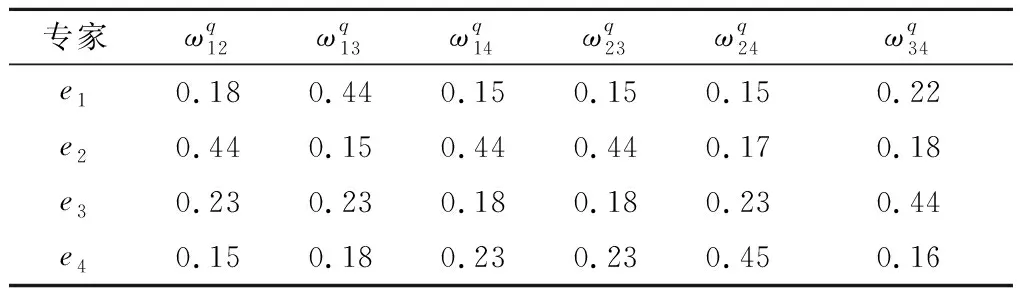
表5 集结权重

则群体意见为

步骤 7运用式(7)计算群体共识度GCI=(GCIij)n×n:

GCI12=0.972,GCI13=0.917,GCI14=0.940

GCI23=0.878,GCI24=0.909,GCI34=0.939

由于GCI23<0.907,则转入步骤8;

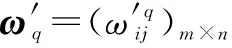
表6 优化决策者集结权重

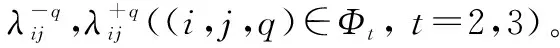
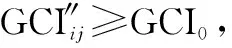
算例 2

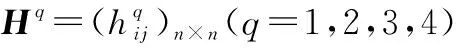
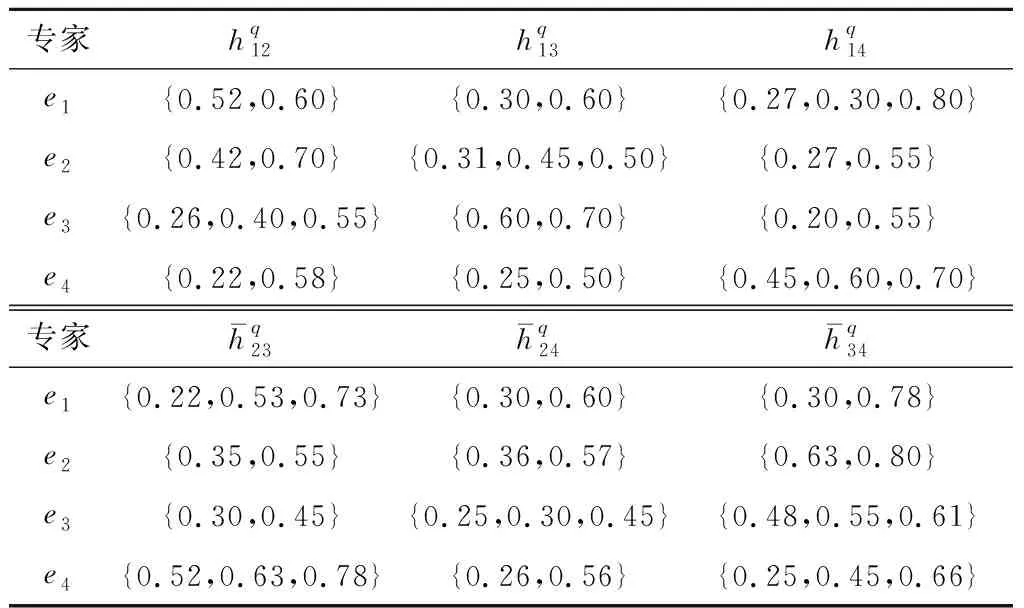
表7 决策群体HFPR评价值(算例2)

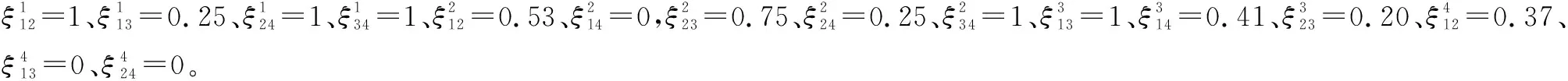
表8 决策者评价值的一致性水平(算例2)

如一致性水平均已达到阈值要求后,转入步骤3。

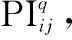
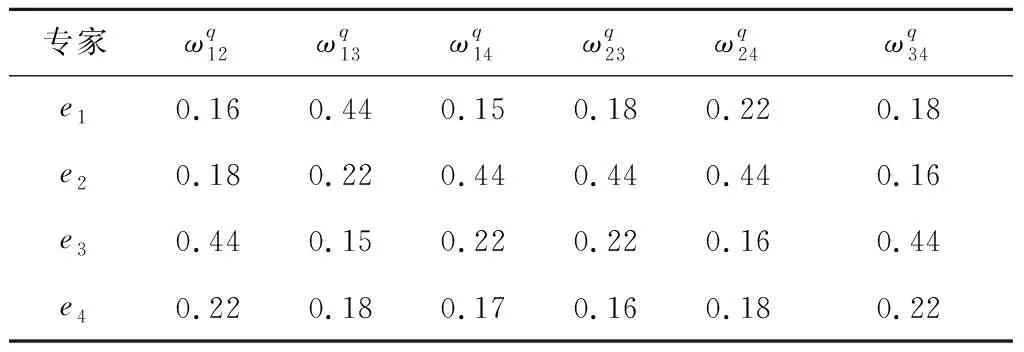
表9 集结权重(算例2)

步骤 4运用式(7)计算群体共识度:GCI12=0.952、GCI13=0.952、GCI14=0.941、GCI23=0.938、GCI24=0.953、GCI34=0.932,由于∀i,j∈N,GCIij≥0.932,则转入第5节中步骤10,完成共识构建。

算例 3

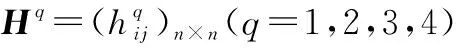
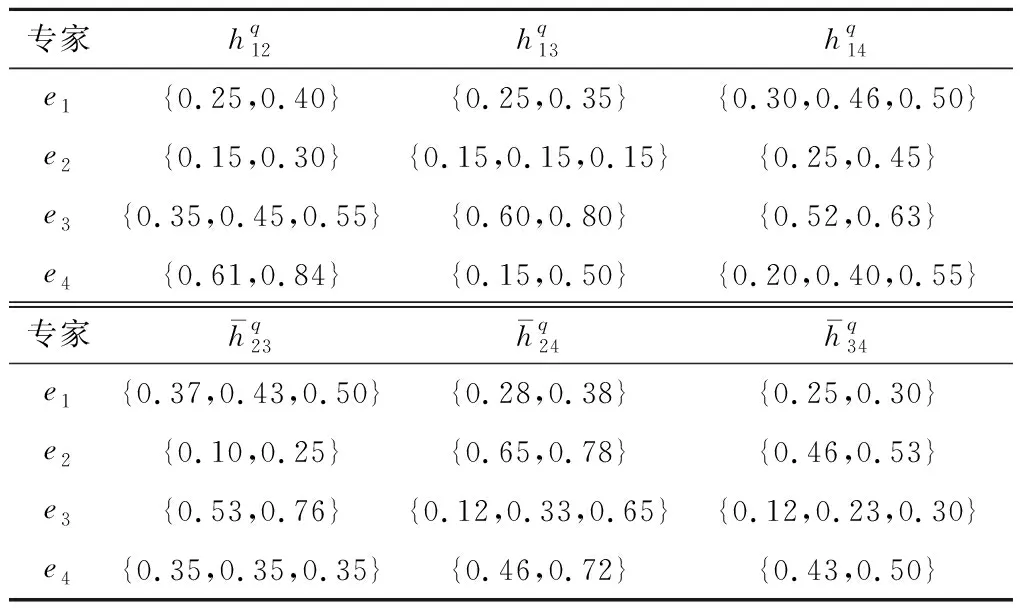
表10 决策群体HFPR评价值(算例3)

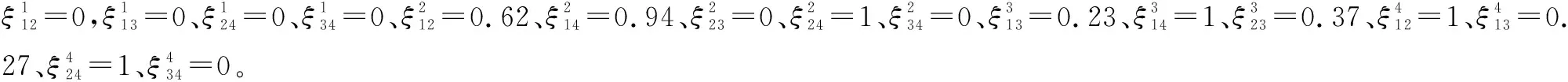
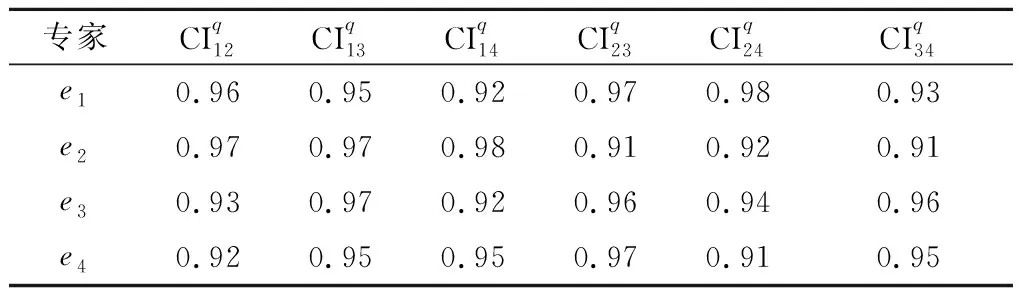
表11 决策者评价值的一致性水平(算例3)

一致性水平已达到阈值要求,转入步骤3。

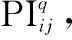
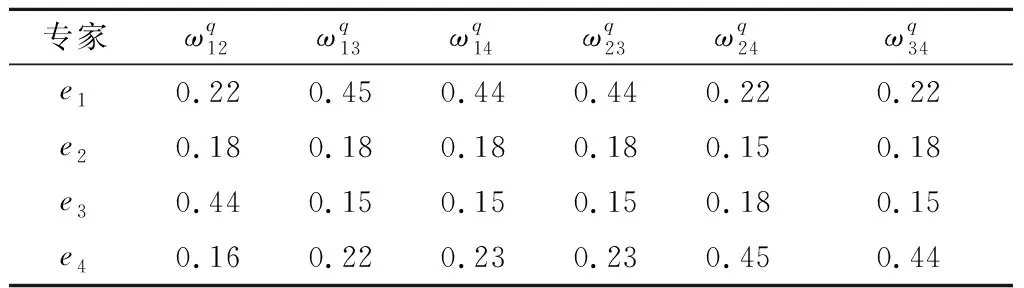
表12 集结权重(算例3)

步骤 4运用式(7)计算群体共识度:GCI12=0.916、GCI13=0.897、GCI14=0.947、GCI23=0.930、GCI24=0.912、GCI34=0.929。由于GCI13<0.905,故转入步骤5,进行集结权重优化;

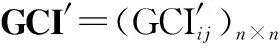
(2) 对比分析

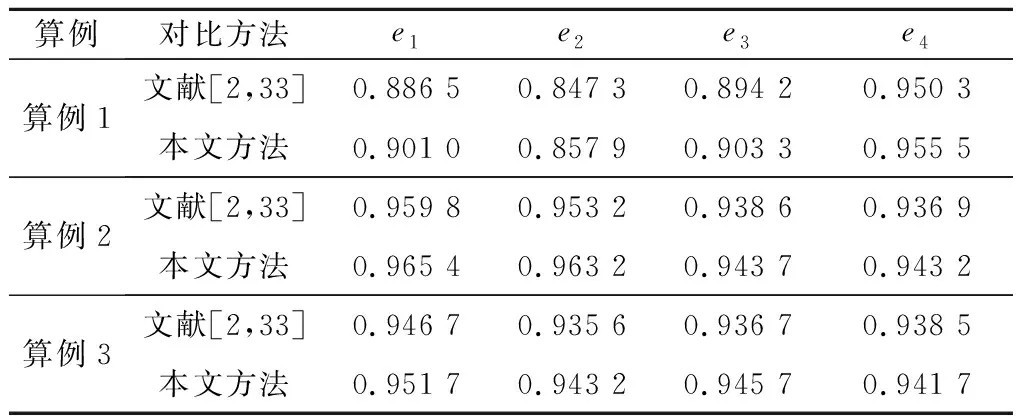
表13 一致性水平对比

由于文献[2,33]方法中未考虑评价值间差异性,标准化后的个体一致性水平均低于本文方法。

(2) 群体偏好集结的共识度水平GCI=(GCIij)n×n。文献[13]以个体一致性水平为诱导值,运用诱导有序集结算子对个体偏好进行集结,文献[13]与本文方法在算例1～算例3中的共识度比较如图2所示。

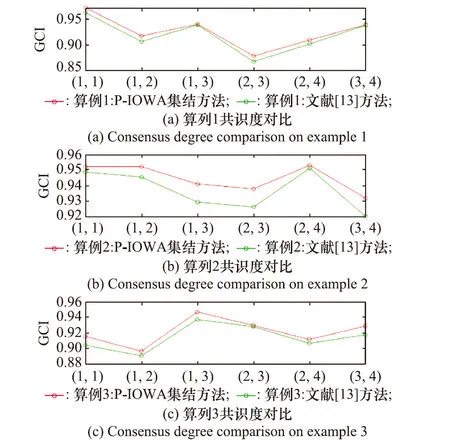
图2 群体共识度对比Fig.2 Group consensus comparison

由于本文以贴进度为诱导值集结个体偏好,同时兼顾各评价值间的差异,群体偏好集结效果更优,在各位置上共识度更高。

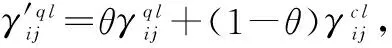
表14 调整距离对比

在算例1中,当θ<0.7时,调整后的个体偏好才满足共识度阈值,其最小调整距离λ=0.823 4,而本文算法的调整幅度仅为λ=0.125 6;在算例2中,本文在偏好集结过程中即满足共识度阈值;在算例3中,本文通过优化集结权重达到共识度阈值,故不对原始评价进行调整,对原始信息的保留程度优于现有方法。

7 结 论

本文以犹豫模糊偏好关系为表征方式,从一致性水平检验、群体偏好集结和群体偏好调整3个阶段,研究了一致性水平、群体共识度以及最小调整量3个目标驱动下的HFPR信息融合方法。通过算例研究与对比分析,本文提出的群体偏好集结方法共识度更高,避免了群体偏好调整时个体一致性水平的降低,同时调整幅度和调整元素数量较少,对实现高度共识、降低调整成本以及优化反馈流程具有重要指导意义。