基于高斯过程模型的多响应稳健参数设计

翟翠红, 汪建均, 冯泽彪

(南京理工大学经济管理学院, 江苏 南京 210094)

0 引 言

近年来,随着半导体、电子自动化和通信等技术的迅猛发展,能够记录和存储数量不断增加的复杂和高维数据的智能传感器不断出现。这些传感器能够获得具有以下特点的数据流[1]:① 多种类,各种类型的传感器产生的数据流种类较多,如波形信号、图像和视频;② 高维度,典型的用于表面检测的图像在1 M像素左右;③ 高速度,近年来数据采集速度显著提高,几乎可以跟上任何生产速度;④ 时空结构,剖面图中的数据点或图像内的像素是空间相关的。这种响应变量称为时空数据、剖面响应或函数响应。通过对流数据进行有效的建模和分析,可以实现实时过程监控、故障诊断和在线产品检测。然而,这些数据流的复杂特性给数据建模与稳健参数设计带来巨大挑战。

20世纪80年代,日本著名的质量工程专家Taguchi博士,在试验设计和信噪比(signal to noise ratio, SNR)的基础上提出稳健参数设计(robust parameter design, RPD)方法。他认为质量特性一旦偏离其设计目标值,就会造成质量损失,且偏离越远,质量损失越大。为了减少产品或过程的波动造成的质量损失,他利用正交表进行试验设计,通过选择可控因子的最佳参数组合,使得产品或过程对噪声因子不敏感。具有复杂特性的剖面响应稳健参数设计与经典稳健参数设计类似,大多通过如Taguchi参数设计、响应曲面等统计建模的方法,研究输入因子与其输出响应之间的关系。此外,各种创造性的方法将其他技术与Taguchi方法相结合,以解决剖面响应优化问题。例如,Tansel等[2]将比率分析的多目标优化与Taguchi方法整合,将多响应问题转化为单响应问题. 不仅减少了Taguchi法中用户决策所需的计算步骤,而且不需要额外的系数,这将降低数学计算的复杂性。少数研究者为了考虑生产过程中多个质量特征之间的相关性,开发了更可靠、更实用的响应面模型,如似不相关的回归模型[3]。Wang等[4]利用贝叶斯似不相关回归模型拟合输入因子与输出响应之间的关系,并综合考虑模型参数的不确定性和制造过程的高变异性,建立一种兼顾报废成本和质量损失的两目标函数,提出了一种在贝叶斯建模和优化框架下的经济参数设计。

由Taguchi[5]开创和倡导的稳健试验设计,已被世界上许多科学家和工程师所接受和研究。但是,Taguchi的稳健设计方法有时需要进行大量物理试验或建立大量原模型。而物理试验只适用于设计因子有限的产品和工艺,且在爆炸性材料的引爆,或者当观察到山体滑坡或飓风等罕见事件时,物理试验是不可行的。为了在全球竞争中求得生存和成功,人们的兴趣和焦点逐渐从物理试验转向了虚拟试验[6]。与物理试验相比在计算机模拟器上进行试验的速度快、成本低,所以计算机试验在电气工程中的集成光子滤波器[7],航空航天工程中的气钉喷嘴[8]和微机电系统装置[9]等工程和科学研究中被广泛应用。然而,在制造业中,计算密集型设计问题变得越来越普遍[10-12]。为了达到与物理测试数据相当的准确性水平,计算机仿真通常很复杂且执行起来非常昂贵。尽管计算能力不断进步,但诸如有限元分析和计算流体动力学等工程分析代码的复杂性似乎与计算能力保持同步,使得综合参数分析非常耗时。因此,迫切需要为计算机仿真模型开发简单的近似模型,即元模型。

元建模方法能够利用有限样本来逼近昂贵的计算密集型函数,在有效降低仿真优化成本的同时保证仿真优化的精度,被广泛用于设计优化[12-16]。为了在有限的样本数量下高效、准确地生成元模型,人们已经进行了大量研究。常用的元模型有多项式回归[17],人工神经网络[18-19],多元自适应回归样条[20],径向基函数[21-22],高斯随机过程(或Kriging模型)[23-24]和支持向量回归[25-26]。然而,输入和输出变量的高维性会给问题建模和优化带来指数级困难,即工作量随维数的增加呈指数增长。假设在n个输入变量的每一个变量中采样s个点,则该采样需要执行sn次计算机试验来建立元模型,这对于计算昂贵型函数的建模显然不太现实。除了计算量大之外,这些模型(函数)对于设计者而言是隐式且未知的,即黑盒函数。函数隐式是设计优化的重大障碍,随着设计问题中变量数量的增加,计算需求也呈指数增长。这种由问题维度带来的困难被称为维数灾难。Mistree研究小组将此困难称为稳健设计或多学科设计优化中的问题规模。而在对由传感系统获得的具有复杂特性的高维数据流进行建模与优化时,要同时克服高维度、计算昂贵以及黑盒函数(high-dimensional, expensive and black-box, HEB)3种困难,严重加剧了问题仿真与优化的难度。Shan等[12]从1 000多篇不同学科论文中筛选出207篇参考文献,对HEB问题的建模和优化策略进行调查。该调查显示:通常,用于HEB的建模技术和优化方法都限于低维问题,对于高维问题的研究比较缺乏。

目前,能够缓解维数灾难问题的常用方法有分解、筛选、映射、空间缩小和可视化等。分解将一个问题重新划分为多个维度较低的子问题,并将子问题重新组合,生成一个元模型[9]。筛选或特征选择利用敏感性分析识别重要的变量,并去除不重要的变量以生成元模型,从而降低问题的维度[12, 27-30]。映射将相关变量的集合转化为更小的集合。而空间缩小则减少了问题的设计范围[12]。上述方法已从并行计算、减小设计空间、筛选重要变量、将设计问题分解为子问题、映射和可视化变量等不同角度缓解高维性所带来的困难。但这些传统的元建模方法对具有HEB特征的复杂和高维数据问题效率低下、精确度低。例如,筛选在降低问题维度和复杂性的同时,可能会导致模型参数估计和预测中信息损失,影响模型精度。而映射虽然可以减少问题的规模和优化的复杂性,但却不能确保在低维空间中获得的最佳方案是原高维空间中的真正最佳方案。因此,面对高维数据的建模与稳健参数设计问题,迫切需要研究新的元建模与参数优化技术。

高斯过程(Gaussian process, GP)是用于近似计算密集型计算机模型的强大工具,具有预测精度高、便于扩展的优点,被广泛用于模拟输入与输出之间的复杂非线性关系。对于已经成为典型的多输入与多输出数据建模与稳健参数设计问题,当不考虑输出之间的相关性时,一种简单方法是为每个输出分别构造一个独立的GP模型。而在许多实际应用中,计算机模型的不同输出级别是相互关联的[31-33]。Qian等[34]提出了构建多变量GP (multivariate GP, MGP)模型的通用框架。框架中的协方差函数是可分离的,并且在所有输出级别上具有共同的边际协方差函数。该假设简化了协方差结构并显著减少了模型参数的数量。Melkumyan等[35]使用不可分的协方差结构对输出进行充分建模。不可分离协方差函数允许不同输出水平使用不同的协方差参数,这比可分离的协方差函数要灵活得多。Li等[36]开发了测试协方差函数可分性的多变量随机字段,这为选择哪种类型的协方差函数提供了理论依据。Sung等[37]提出一种多分辨率函数方差分析模型,作为一种计算上可行的仿真替代方法。这个模型可以用于大规模和多输入的非线性回归问题。Chen等[38]使用GP对具有时空相关结构的高维输出变量进行建模,提高了量化模型自身不确定性的能力和模型预测精度。Ghosh等[39]提出基于线性混合效应(linear mixed effects, LME)的多变量剖面建模方法,使用MGP控制的B-splines曲线构建LME模型中的随机部分。与传统的MGP和LME方法相比,该方法在未增加大量参数的情况下实现了剖面建模的灵活性。Li等[40]针对高维参数空间和大规模协方差矩阵问题,提出了一种成对建模方法,该方法充分利用超球面分解的序列构造特点,将高维MGP模型分解为一系列的二元GP模型。随后,冯泽彪等[41]针对预测偏差和波动的多响应稳健参数设计问题,结合超球面分解理论和成对估计超参数方法建立MGP预测模型。提出了综合考虑质量损失和期望概率的多响应稳健参数设计方法。然而,MGP模型经常面临巨大协方差矩阵造成的数值问题和计算挑战。此外,估计GP模型相关函数中的参数的标准方法,如最大似然估计(maximum likelihood estimation, MLE),通常会产生不稳定的结果,从而导致预测结果较差。使得MGP模型在大型和复杂问题上的实际应用中受到限制。

本文针对高维试验数据的稳健参数设计问题,在GP的建模框架下,采用部分平行的GP (parallel partial GP, PPGP)模型来构建试验因子与多质量特性之间的响应曲面,在此基础上运用多元质量损失函数作为优化指标来获得可控因子的最佳参数设计值。首先,利用符合稳健参数估计标准的边缘后验估计方法,估计GP模型中的相关参数,并使用从总体似然中估计的共同相关参数,建立每个坐标位置概率上独立的PPGP模型[42]。然后,使用PPGP模型构建试验因子与多质量特性之间的响应曲面,结合PPGP模型部分平行的特征,基于SNR的方法构建多元质量损失函数。最后,结合PPGP模型和多元质量损失函数建立多响应优化模型,并使用遗传算法获得可控因子的最佳参数设计值。此外,通过仿真算例和实际案例验证了所提方法的有效性和便捷性。与独立建模的单变量GP模型相比,本文采用联合建模方法不仅能够有效地处理高维试验数据的建模与参数优化问题,而且能够获得更为稳健的优化结果,运行效率更高。

1 高斯过程模型原理

设X为输入空间,x∈X表示k维输入因子,对应的输出响应y(x)视为一个通过GP建模的未知函数:

y(·)～GP(μ(·),C(·,·))

(1)

式中:μ(·)为均值函数;C(·,·)=σ2c(·,·)为协方差,σ2和c(·,·)分别为方差及相关函数。

对来自X的任意输入因子组合{x1,x2,…,xm},其似然函数服从下面的多元正态分布:

(y(x1),y(x2),…,y(xm))T|μ,σ2,R～

MVN((μ(x1),μ(x2),…,μ(xm))T,σ2R)

(2)

式中:σ2是未知方差;R是(i,j)元素为c(xi,xj)的相关矩阵。

通常通过回归对均值函数建模:

(3)

式中:h(x)=(h1(x),h2(x),…,hq(x))是指定基函数的向量;θt是基函数ht的未知回归参数。对于输入xi=(xi1,xi2,…,xik)和xj=(xj1,xj2, …,xjk),常用的相关函数是以下形式的指数族相关[43]:

(4)

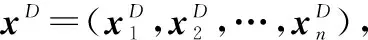
为了处理未知的均值和方差,简单地利用位置-尺度参数的标准参考先验,即

(5)

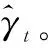
(6)

对应的密度函数[46-47]为

其中,

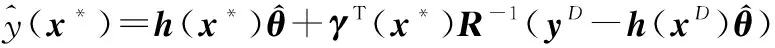
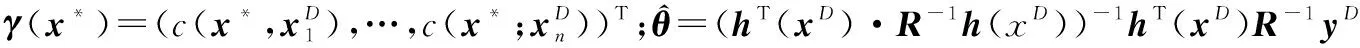
2 结合部分平行高斯过程模型与质量损失的稳健参数设计

2.1 基于部分平行高斯过程建立响应曲面

为了提高计算效率和预测精度,本文采用联合建模的PPGP方法替代独立建模的单变量GP方法,来拟合多输入和具有时空结构的多输出计算机模型。令p表示每次预测所考虑的时空网格点总数,为每个坐标分别建立一个概率上独立的式(1)形式的模型。对于均值和方差参数,我们使用相同的标准目标先验:

(7)

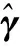
(8)

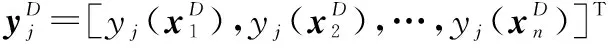
2.2 多元质量损失函数

Taguchi使用信噪比作为评估产品质量稳定性的重要指标,信噪比越大,产品质量越稳定,造成的损失越小。望目、望小和望大3种质量特性的信噪比分别为

(9)

(10)

ηL=10lg(σ2+u2)

(11)

式中:μ和σ2分别是产品质量特性y的均值和方差。

为了近似描述波动造成的质量损失,Taguchi定义了二次质量损失函数:

L(y)=k(y-T)2

(12)

式中:k=A/Δ2,其中A为质量偏差造成的经济损失,Δ为质量偏差。

Artiles-león[48]为使损失函数不受其单位影响,令Taguchi的二次质量损失函数中的系数k=4/(U-L)2,提出了无量纲的标准化多元质量损失函数:

(13)

式中:Ti,Ui,Li分别为质量特性yi的目标值和上、下规格限。

Pignatiello[49]根据最小化偏离设计目标值的偏差和最大化稳健性原则,在Taguchi单变量质量损失函数的基础上,提出了多元二次损失函数:

L(y(x))=(y(x)-T)TC(y(x)-T)

(14)

式中:y=(y1(x),y2(x),…,yp(x))T为p个响应构成的p×1维向量;T=(T1,T2,…,Tp)T为p个响应的目标值构成的p×1维向量;C为反应过程经济成本的p×p维正定矩阵。

文献[50]指出,使用Taguchi的信噪比方法度量稳健性能时效率低,有时信息损失较大。虽然Artiles-len在Taguchi的二次损失函数基础上,提出的无量纲损失函数具有较多优点,但将每个变量等同对待,进行简单的求和计算,没有考虑各响应变量之间的相关结构。尽管Pignatiello的多元二次质量损失函数考虑了不同响应变量之间的相关结构,但仅适用于“望目”质量特性,对于在实践中经常遇到的“望小”和“望大”质量特性均不适用。

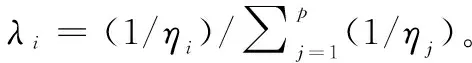
(15)

LL(y(x))=

(16)

LT(y(x))=

(17)

令:

则式(15)～式(17)可以统一为如下形式:

(18)

式中:λi和L(yi(x))分别为第i个质量特性yi的损失权重和损失函数。

2.3 结合部分平行高斯过程模型与质量损失的参数优化

在PPGP建模框架下,结合本文所提出的多元质量损失函数,构建多响应优化模型:

(19)

式中:各变量解释与前文一致。然后,使用遗传算法寻找优化模型的全局最优参数设计值。鉴于篇幅有限,文中所用程序代码和相关试验数据未放入正文。

结合PPGP模型与质量损失的稳健参数设计基本流程如图1所示。

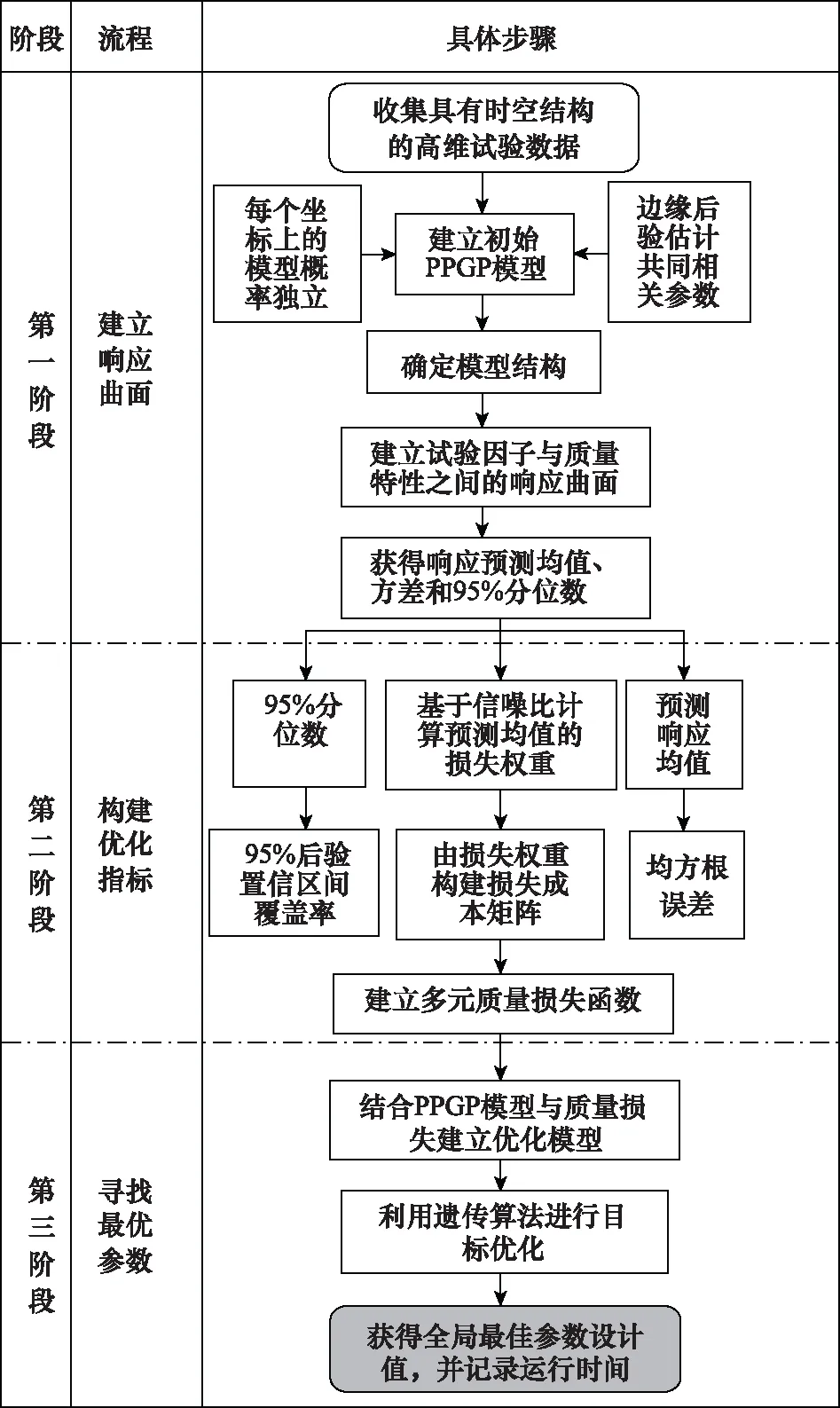
图1 结合PPGP模型与质量损失的稳健参数设计流程图Fig.1 Flow chart of robust parameter design combining PPGP model and quality loss

具体步骤如下。

步骤 1收集具有时空结构的高维试验数据,利用试验数据建立初始PPGP回归模型。

步骤 2利用边缘后验估计法近似模型超参数,确立PPGP模型,并使用PPGP模型构建试验因子与质量特性间的预测响应曲面,如式(2)～式(8)所示。

步骤 3结合PPGP模型部分平行的特征,利用信噪比计算各预测响应均值的损失权重,由损失权重生成的对角矩阵作为损失成本矩阵,构建多元质量损失函数。如式(9)～式(11)及式(18)所示。

步骤 4结合PPGP模型和多元质量损失函数构建多响应优化模型,如式(19)所示。

步骤 5使用遗传算法,在输入变量可行域内为多响应优化模型寻找全局最优参数设计值,并记录其运行时间。

步骤 6获得高维复杂试验数据的建模与参数优化问题的有效方法,得到的优化结果更稳健,运行效率更高。

3 仿真与实证研究

本节使用一个仿真算例和电动交流发电机(望目)、金属注射成型(望大)两个应用实例来说明本文方法的预测能力、有效性和便捷性。并选择单变量GP方法作为对比方法,使用如下标准评价两种方法样本外预测和不确定性量化的准确性。

(1) 绝对偏差

(20)

(2) 多元质量损失函数

(21)

(3) 均方根误差

(22)

(4) 95%后验置信区间覆盖率

PCI(95%)=

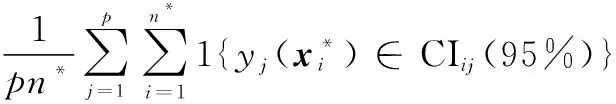
(23)

3.1 仿真算例

3.1.1 仿真函数

仿真试验虚拟图书馆为评估计算机模型的试验设计和分析的新方法,提供了一套函数和数据集。本文在此网站上选取Cross-in-Tray,Bohachevs-ky,McCormick和Easom 4个经典复杂二元函数构建仿真案例,对本文方法和单变量GP方法的性能进行测试。4个测试函数的过程参数xi∈[-10,10],i=1,2。质量特性yj的取值范围长度分别为R1=1.812 6,R2=297.138 6,R3=444.117 5,R4=1.009 0。考虑到随机噪声的水平对基于GP的优化算法有很大影响,本文根据质量特性yj的取值范围长度Rj的大小,设定各函数的随机噪声水平分别为:ε1,ε4～N(0,0.000 12),ε2,ε3～N(0,0.0012)。测试函数的具体设置如表1所示。

表1 测试函数详情

如图2中第一行的二维曲面图所示,这4个测试函数的选取涵盖了4个不同的形状特征。Cross-in-Tray函数由于存在大量局部极小值而难以优化;Bohachevsky函数图像类似于碗状;McCormick函数图像类似于盘状;Easom函数图像陡降,虽然是单峰的,但有多个局部极小值,且局部极小值的搜索空间很小。图2中的第二行为各测试函数的等高线图,红色星号代表取得最优解的位置。

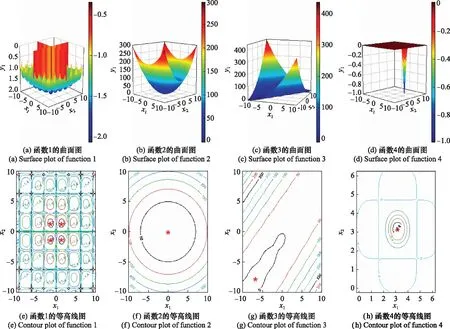
图2 4个测试函数的曲面图和等高线图Fig.2 Surface and contour plots of four test functions

3.1.2 仿真结果

使用最大最小拉丁超立方体(maximin Latin hypercube,maximin LH)设计在[-10,10]×[-10,10]上生成240组二维随机样本,前40组用来拟合PPGP模型和单变量GP模型,后200组用来做样本外预测,仿真结果如表2所示。

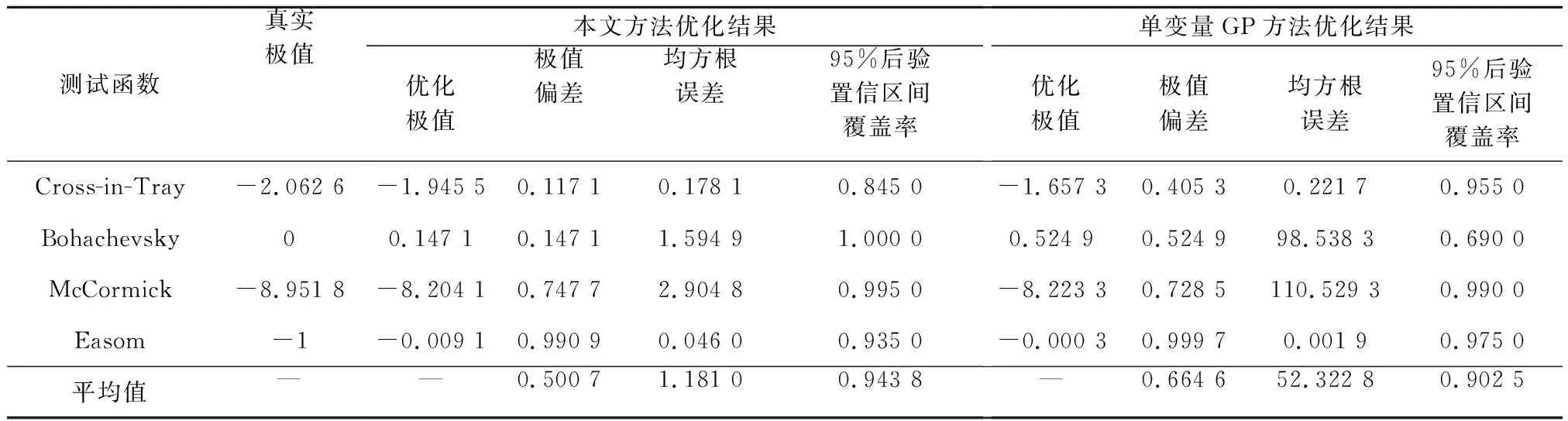
表2 模型优化结果对比

3.2 实证研究案例

3.2.1 实例1(望目) 电动交流发电机试验

该试验案例来源于文献[51],主要研究电动交流发电机的稳健参数设计问题。试验由8个控制因子xc=(x1,x2,…,x8)T、两个噪声因子xn=(x9,x10)T和一个信号因子s组成,各因子具体设置如表3所示。试验中感兴趣的响应是交流发电机在7个不同转速(revolutions-per-minute, RPM)下运行时产生的电流。7个质量特性均属“望目”类型,表4中的U(sj),L(sj)和T(sj)分别为电动交流发电机在转速sj下产生的电流上、下规格限及目标值。试验者采用TaguchiL18正交阵列设计,并将其重复6次开展相关试验。

表3 因子列表

表4 电动交流发电机在不同转速下电流的上、下规格限及目标值

试验的目标是找到控制因子与噪声因子的最佳参数组合,使得各转速下的电流均值尽可能接近设计目标值的基础上,最大限度地减少质量特性围绕设计目标值的波动。针对该目标,按照第2.3节中的优化模型构建步骤,使用本文方法和单变量GP方法对该试验数据进行建模与优化。选用遗传算法寻找多响应优化模型的全局最优参数设计值,并记录其运行时间。其中,最大迭代次数设置为1 000,在优化停止之前最优解没有任何改进的情况下,连续迭代次数设置为100。搜索空间的上、下界分别设为(1,1,1,1,1,1,1,1,1,1)和(-1,-1,-1,-1,-1,-1,-1,-1,-1,-1),其他设置选择默认,优化结果如表5所示。 另外,为了与Alshraideh等[52]提出的高斯随机函数(Gaussian random function, GRF)方法进行比较,将其得到的优化参数设计值对应的优化结果放入表5,以便对比分析。

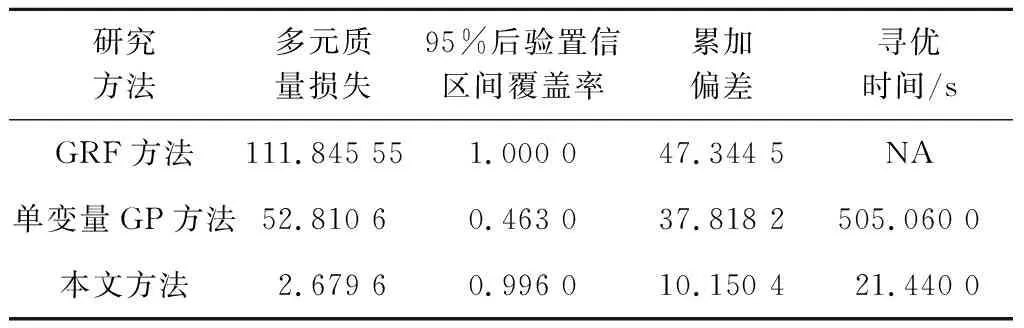
表5 交流发电机案例不同研究方法的优化结果

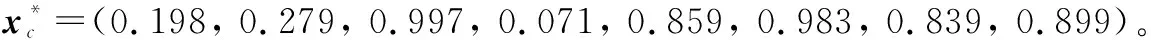
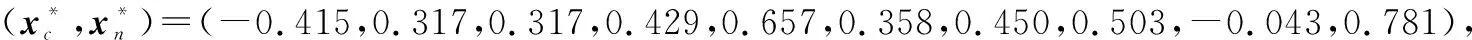
图3是3种不同方法下获得的优化参数组合对应的预测均值剖面图,下面简称优化预测剖面图。结合图例,可直观地看出3种方法获得的优化预测剖面(黑色点线)均落在上、下规格限(红色虚线)及其对应的上、下95%分位数线(蓝色点线)范围内。但本文方法获得的优化预测剖面处在其他两种方法的优化预测剖面之间,波动较小,且与该试验的目标值剖面(青色实线)更接近。更直观地说明本文所提方法的优化结果从位置与散度两方面来看,均优于其他两种方法。

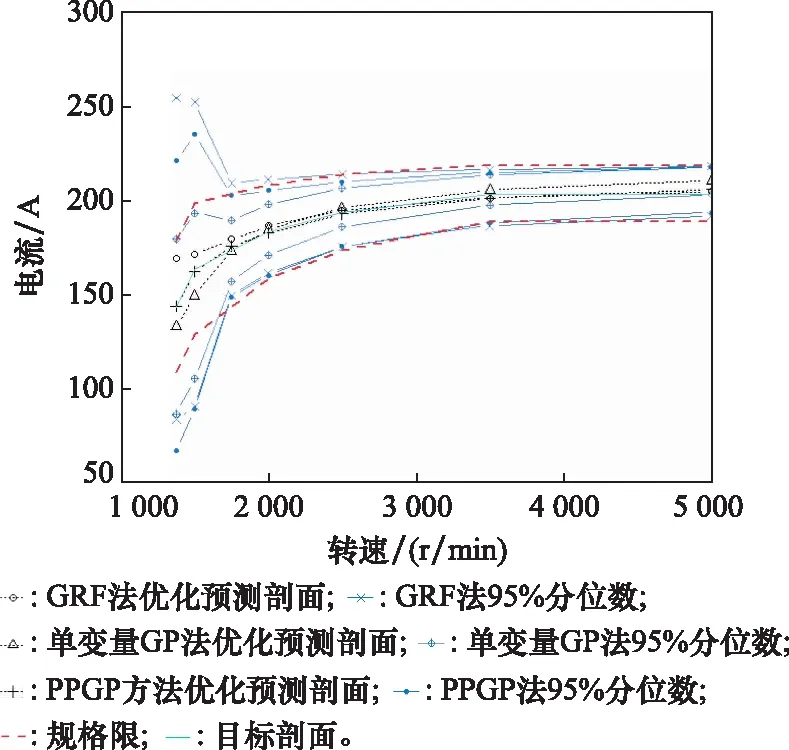
图3 交流发电机试验3种方法下的优化预测剖面图Fig.3 Optimized prediction profiles of alternator experimentunder three methods

3.2.2 实例2(望大):金属注射成型工艺试验

Govaerts和Noel在文献[53]中介绍了金属注射成型试验案例,该试验在金属注射成型过程中观察到25个“绿色”零件(烧结操作前的产品),在10～80 ℃的脱脂温度范围内的701个值(信号因子s)处的凝胶强度(响应y)的剖面。试验由粘合剂成分中的两个可控因素组成,分别是黄原胶浓度(可控因子x1,从1～5在5个水平上变化)和铬与黄原胶浓度比(可控因子x2,从1∶1至4∶1在4个水平上变化)。据作者介绍,其中一个剖面是明显的离群剖面,因此将其排除在分析之外。为了加快计算速度,作者通过每9个观测值采样一次,即信号因子s的水平数从701降为78。由于该工艺旨在确定黄原胶和铬两种成分的最佳组合,使在低凝胶温度(避免过度蒸发)的条件下获得尽可能大的胶凝强度。因此,上述试验中的响应y属于“望大”类型。使用本文方法和单变量GP方法,按照第2.3节中的优化模型构建步骤,对该试验的数据进行建模与优化。选用遗传算法寻找多响应优化模型的全局最优参数设置,并记录其运行时间。其中,最大迭代次数设置为1 000,在优化停止之前最优解没有任何改进的情况下,连续迭代次数设置为100。搜索空间的上、下界分别设为(5,4)和(1,1),其他设置选择默认,优化结果如表6所示。另外,为了与Alshraideh等[52]提出的GRF方法进行比较,将其得到的优化参数设计值对应的优化结果放入表6,以便对比分析。

表6 金属注射成型试验不同研究方法的优化结果

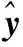
图4左侧是3种不同方法下获得的优化参数组合对应的优化预测剖面图。结合图例,可直观地看出三种方法获得的优化预测剖面(黑色点线)均落在上、下规格限(红色虚线)及其对应的上、下95%分位数线(蓝色点线)范围内。图4右侧是对左侧图中[42,50]×[9,10.5]矩形区域内图像的放大。在右侧的放大图上可清楚地观察到,虽然三种方法获得的优化预测剖面图比较接近。但使用本文方法获得的优化预测剖面位于其他两种方法的优化预测剖面上方,且波动较小。更直观的说明,本文方法不但可以在较低的凝胶温度条件下获得更高的胶凝强度,而且最大限度地减少了质量特性围绕设计目标值的波动,实现了该试验的初始目标。

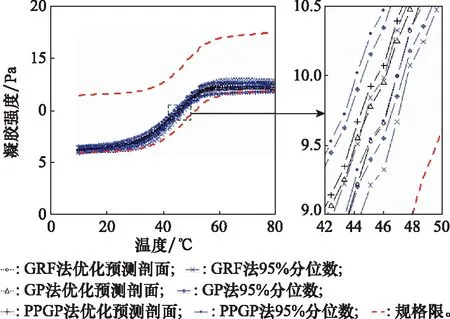
图4 金属注射成型试验3种方法下的优化预测剖面图Fig.4 Optimized prediction profiles of metal injection molding experiment under three methods

4 方法讨论

本文针对高维复杂数据的建模与稳健参数设计问题,在PPGP的建模框架下,结合多元质量损失函数构建一个新的多响应优化模型。首先,利用边缘后验估计获得超参数的近似值,确立PPGP元模型。其次,结合PPGP模型部分平行的特征,基于信噪比方法计算各响应的损失权重,由损失权重生成的对角矩阵作为成本矩阵,构建多元质量损失函数。最后,在PPGP建模框架下,结合多元质量损失函数构建多响应优化模型,并使用遗传算法寻找全局最优参数设置。此外,通过仿真试验与工程案例,将本文所提方法与基于最大似然估计的单变量GP方法和Alshraideh等[52]提出的GRF方法进行比较。发现本文所提方法,得到的质量损失和绝对偏差最小,95%后验置信区间更接近95%的名义水平。更重要的是,由于本文方法采用联合建模的思想,与独立建模的单变量GP方法相比,在建模时更方便,用遗传算法寻找最优解时所用的时间更短。说明本文所提方法能够较好地兼顾建模和优化过程的便捷性和稳健性。而且随着数据量和维数的增加,本文方法的优势愈明显。

5 结束语

针对高维试验数据的建模与稳健参数设计问题,本文在GP的建模框架下,采用PPGP模型来构建试验因子与多质量特性之间的响应曲面,在此基础上运用多元质量损失函数作为优化指标来获得可控因子的最佳参数设计值。另外,通过仿真试验与工程案例,将本文所提方法与单变量GP方法和Alshraideh等提出的GRF方法进行比较。研究结果表明:与独立建模的单变量GP方法相比,本文采用联合建模方法,不仅能够有效地处理高维试验数据的建模与参数优化问题,而且能够获得更为稳健的优化结果,运行效率更高。可以有效缓解高维复杂数据建模的“维数灾难”和优化的复杂性等困难。

需要特别指出的是,本文所提方法的部分平行特点是简化计算的关键,可以有效地处理响应服从正态分布的试验数据的建模与稳健参数设计问题。但若试验数据存在明显的空间相关性或为非正态响应时,本文方法不再适用。希望改进模型以扩大其适用范围,以便本文方法能够更好地解决现实问题。另外,如何使用PPGP模型有效地处理既有定量因子又有定性因子的高维混合效应试验的质量设计问题,是未来有待深入研究的课题之一。