基于趋势估计的微多普勒分离与特征提取算法
彭正红, 杨德贵,*, 王 行, 王 浩, 朱政亮
(1. 中南大学航空航天学院, 湖南 长沙 410083; 2. 中南大学自动化学院, 湖南 长沙 410083;3. 浙江大学工业控制技术国家重点实验室, 浙江 杭州 310027;4. 厦门大学水声通信与海洋信息技术教育部重点实验室, 福建 厦门 361005)
0 引 言
现代战场环境日益复杂,诱饵与弹头的结构与特性越来越相似,如何有效识别真假目标成为研究现代电子战的重中之重。随着超宽带雷达技术、雷达信号处理技术等的快速发展,现代雷达能够提供更加精确的目标信息,其中就包括因目标微动引起的微多普勒(micro-Doppler,m-D)特征,这些特征的提取问题也就变得十分重要。通常,m-D特征提取研究工作分为微动信号建模、m-D曲线分离及微动特征提取3个方面。
雷达目标微动及m-D的概念是由Chen首先提出的,并针对这一问题开展了大量研究[1-2],为后来者的研究提供了坚实基础。文献[3]针对进动目标,推导了其m-D频率理论公式,并对锥体弹头m-D特性进行了仿真分析。文献[4]就有翼弹头和无翼弹头进动对雷达回波的影响,进行了理论分析和微波暗室实验。文献[5]针对目标自旋、进动及章动3种微动形式下瞬时频率的差异提取出4种特征,采用支持向量机(support vertor machine,SVM)分类器对3种微动形式进行了有效分类。
对于微动特征提取的问题,目前应用较为广泛的是模态分解方法[6-9]。利用经验模态分解(empirical mode decomposition, EMD)[10]、变分模态分解(variational mode decomposition,VMD)、改进型模态分解方法[11-13]等分解出m-D曲线中的固定模态,经过相应计算获得目标的微动特征。然而,由于目标上不同区域散射点微动形式存在差异,产生的m-D曲线会出现复杂的交叠现象,如果不能对m-D曲线进行精确分离,就会给后续微动特征和参数估计造成困难。
为了解决m-D曲线的交叠问题,学者们提出了许多方法。目前较为常见的方法是根据能量峰值进行提取分离[14],但是对曲线交叠处的分离情况较差。也有利用Viterbi算法[15]、最近邻原则[16]逐条提取m-D曲线的方法,但同样存在曲线交叠处分离效果差的情况。为解决交叠处m-D曲线分离效果差这一问题,文献[17-18]提出了一种曲线路径重组加固有线性调频成分分解方法,分离出m-D曲线,但该方法需要提前知晓m-D曲线的数量,并且针对的是一维信号数据,具有一定的局限性。
针对目标m-D曲线交叠处分离效果差这一问题,本文提出一种基于曲线趋势估计的m-D曲线分离和特征提取算法。首先建立目标等效散射点章动模型以及回波模型,获取目标m-D曲线;然后通过形态学处理获得稳定精细的二值化曲线,利用曲线光滑性及插值理论对曲线趋势进行精确估计,并对其进行有效分离;最后在获得各散射点的m-D曲线的基础上,利用VMD算法分解出各个曲线的所有模态并与EMD分解结果进行对比,估算出各个散射点的各种微动频率。
1 复杂运动目标微动回波模型
1.1 复杂运动目标散射点微动模型构建
雷达目标的m-D效应是由目标的微动引起的,通常目标微动可分解为自旋、锥旋以及章动。为简化分析,假设弹头的形状为圆锥形,诱饵的形状为圆锥形和杆状,建立坐标系如图1所示。图1中,O-XYZ是雷达坐标系;O′-XYZ是参考坐标系,原点O′位于雷达坐标系方位角为ν、俯仰角为α、距离为R0的位置,与雷达坐标系平行;O′-xyz是目标本体坐标系,z轴为锥体目标对称轴,也是其自旋轴l;u轴是目标的进动轴,进动角为θ;w轴是章动轴,是l与u的叉乘。
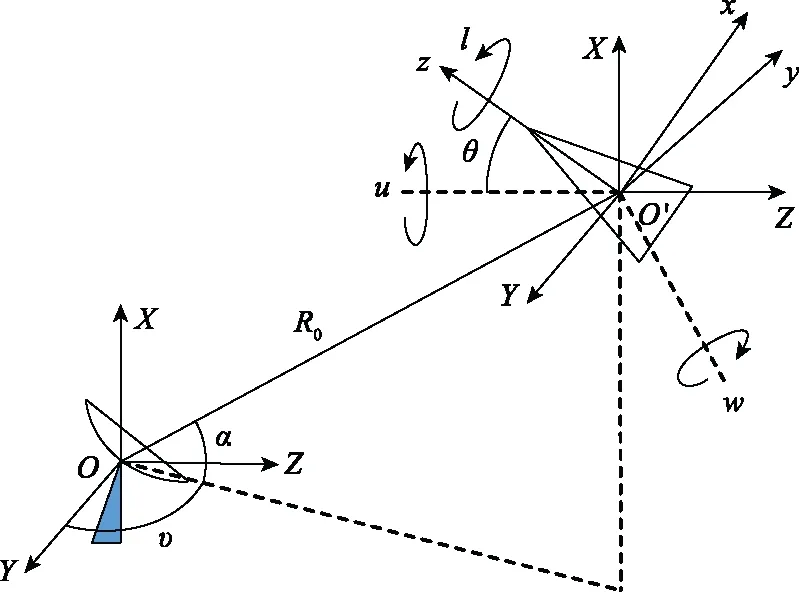
图1 目标微动模型Fig.1 Target micro-motion model
假设l轴在本体坐标系中的单位矢量为l=(lx,ly,lz)T,u轴在参考坐标系中的单位矢量为u=(uX,uY,uZ),雷达视线在参考坐标系中的矢量表示为r=(rX,rY,rZ),目标上一点在本体坐标系中的坐标为p0=(x0,y0,z0),目标自旋角速度为ω1,进动角速度为ω2,章动角速度为ω3。根据文献[19]中所提方法,可以得出目标在运动过程中,各点在参考坐标系中的实时坐标为
(1)
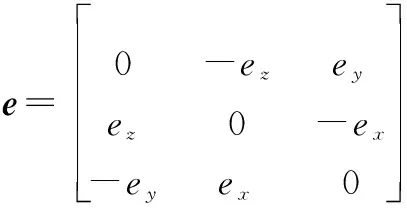
(2)
则目标上各点到雷达的实时距离为
R(tm)=R0+P(tm)n
(3)
式中:n=[-cosαcosν,-cosαsinν,-sinα]
1.2 雷达回波模型构建及回波生成
采用大时宽带宽积的线性调频信号:
(4)
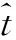
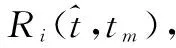
(5)
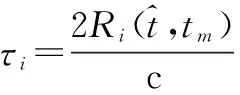
对回波信号作解线频调处理,设参考信号为
(6)
(7)
按照文献[20]中的方法补偿掉剩余视频相位项和斜置项,得到目标混频信号为
(8)
对快时间进行傅里叶变换,得
exp[j2πfc(τ0-τi)]
(9)
2 基于趋势估计的m-D曲线分离
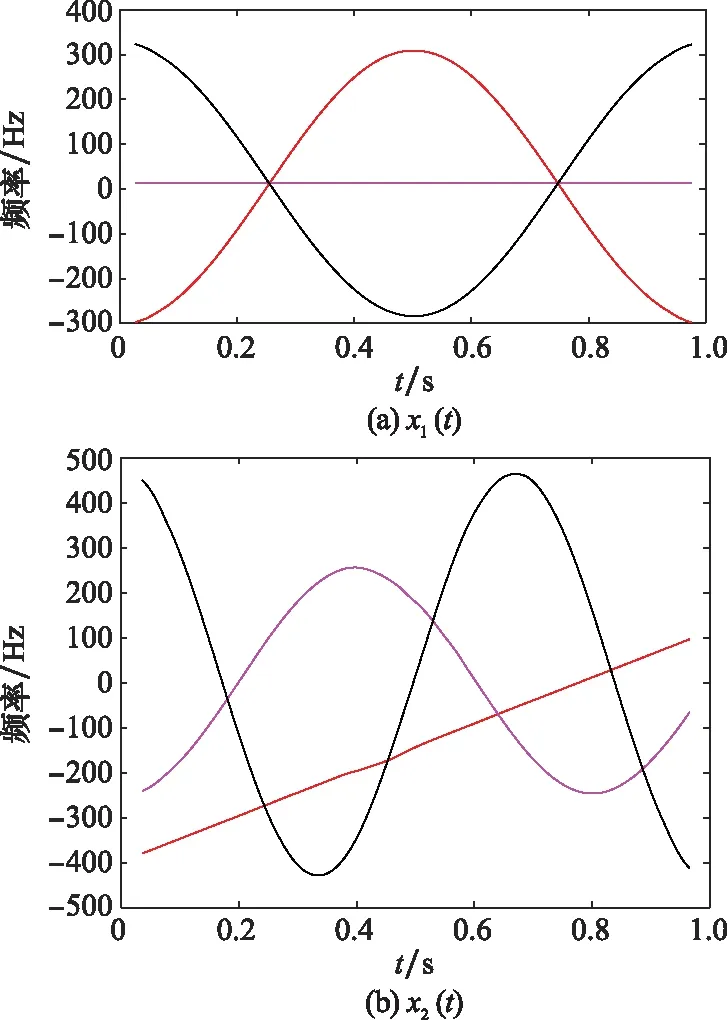
对于包含多种分量的微动信号而言,其m-D曲线都有可能存在交叠情况。假设某一微动信号x1(t)包含一个零频分量和两个相位相反的正弦分量,计算信号的m-D,结果如图2所示。观察图2可以发现,3种分量的m-D曲线在某一点(或区间)处存在交叠情况。
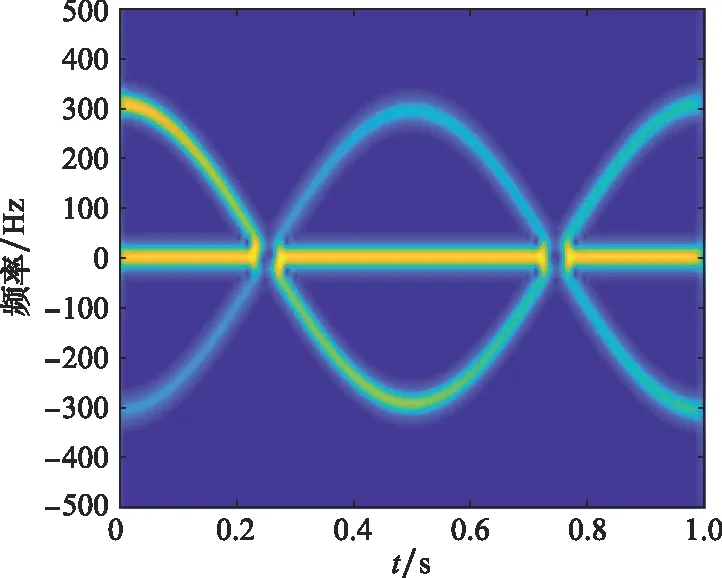
图2 信号x1(t)的m-D图Fig.2 m-D diagram of signal x1(t)
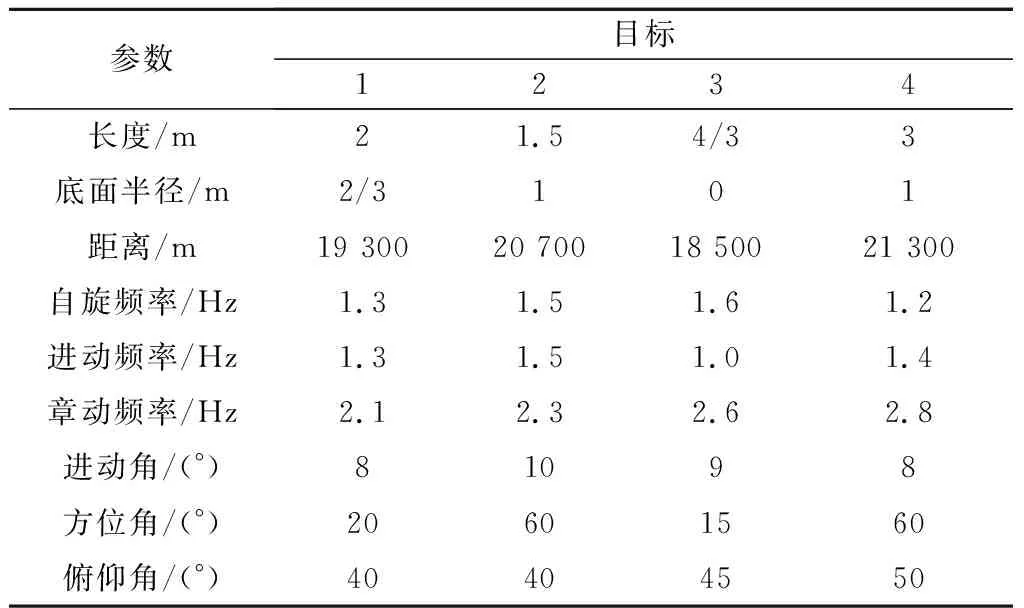
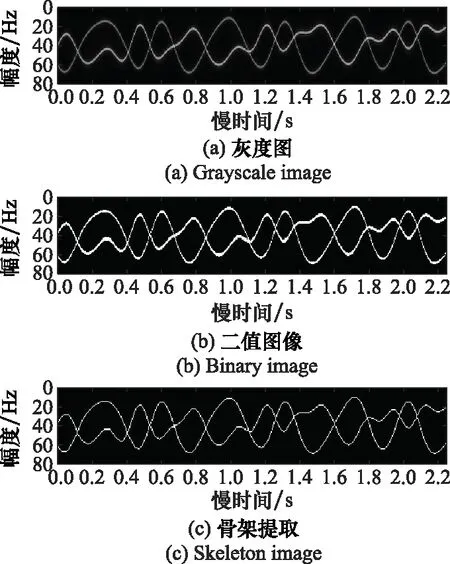
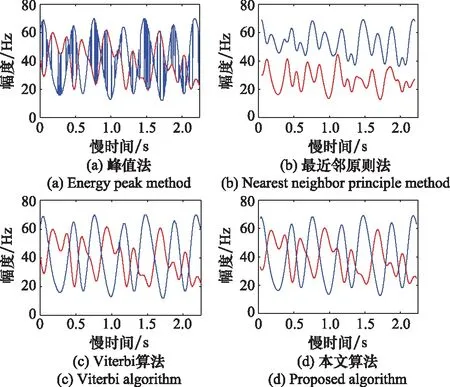
现有m-D曲线分离方法诸如最近邻原则法、Viterbi算法、峰值法等,在进行分离时,均会产生非完全分离、分离效果差的现象,如图3所示。为解决这一问题,本文提出了一种基于曲线趋势估计的分离算法。首先通过骨架提取获得稳定的二值化曲线,再利用曲线光滑性和插值理论对曲线进行分离,具体算法如下所示。
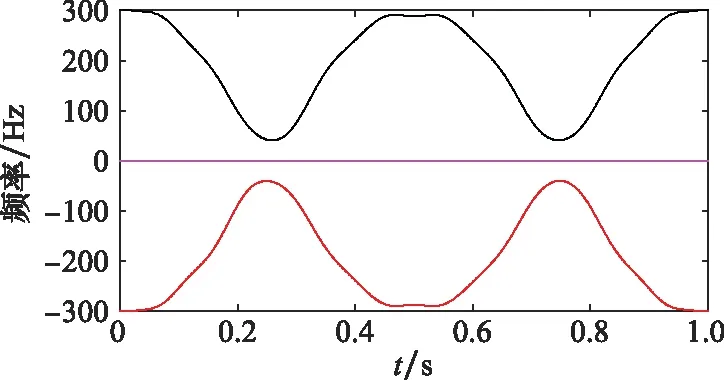
图3 传统算法分离效果Fig.3 Separation effects of traditional algorithms
2.1 骨架提取
首先根据目标回波信号获取其m-D曲线,然后运用形态学图像处理中的骨架提取算法对m-D曲线进行“变细”操作。骨架提取算法的基本思想就是“腐蚀”运算和“开”运算,可表示为
(10)
式中:Θ表示“腐蚀”运算;°表示“开”运算;|Sif(f,tm)|ΘkB表示连续k次对|Sif(f,tm)|进行 “腐蚀”运算;K=max{k|(|Sif(f,tm)|ΘkB)≠∅}表示使|Sif(f,tm)|不是空集的最大“腐蚀”次数。
为防止m-D曲线毛刺对骨架提取算法的干扰,先将获得的m-D曲线进行二值化和高斯平滑处理,再进行骨架提取。
2.2 曲线趋势估计及分离
骨架提取得到最“细”的二值化m-D曲线后,利用“清除”思想将各散射点的m-D曲线分离出来。设获得的m-D曲线数据矩阵为NNr×Na,逐列提取NNr×Na中数据。理想情况下,估计后续点的值可通过判断前一段区间内的导数值(即曲线光滑性)来进行,区间长度i0可根据实际分离曲线的周期进行修整。然而,由于交叠区间的存在及骨架提取得到的m-D曲线交叠区间并非单位长度,导致上述方法无法进行有效分离,因此本文将曲线的交叠区域和非交叠区域分开估计,具体步骤如下。
步骤 1计算需分离的曲线数量
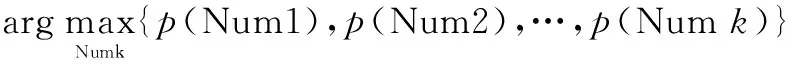
(11)
式中:p(Numi)是各列极值点数量出现的概率。
步骤 2数据优化处理,初步确定交叠区间
当numi>curve_number,剔除多余极值点;
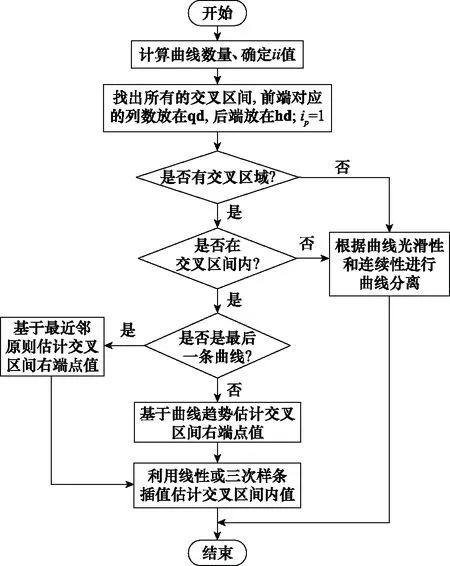
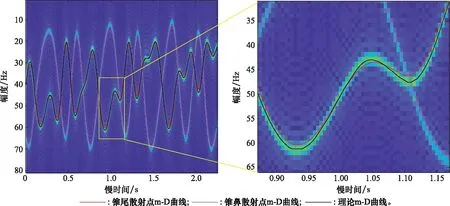
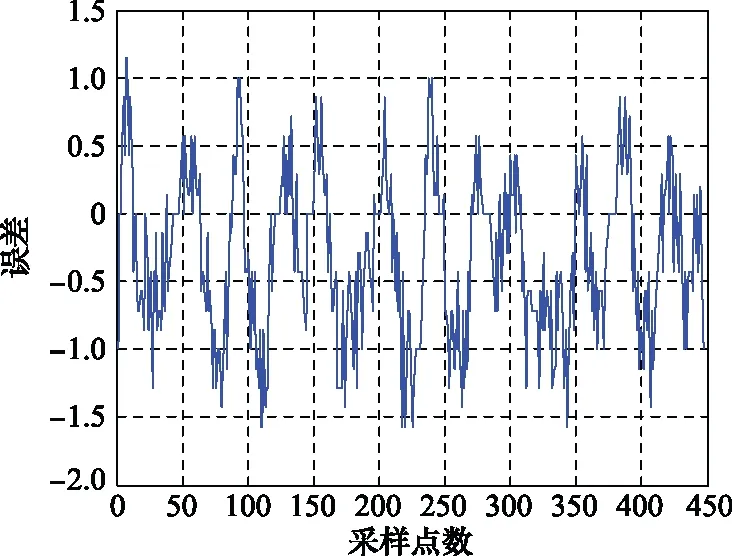
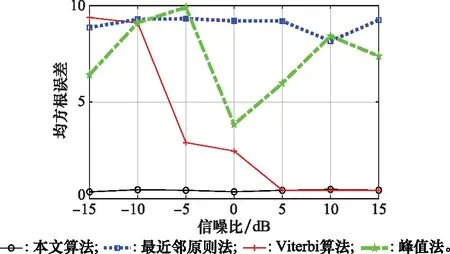
当numi 当numi=curve_number,判断相邻两条曲线之间的距离,若小于阈值ΔmD(整数),视为交叉区间,N(:,i)=0,否则不作处理,即: N(rm(m),i)-N(rm(n),i)<ΔmD,m=1,2,…,numi-1; (12) 上述确定的交叉区间的左右端点分别存储在行向量qd和hd中。 步骤 3截取数据,优化交叠区间。截取中间93%以上的数据,截取后第一列记为ii;合并相邻较近及单位长度的交叠区间,即当qd(i)-hd(i-1)≤3或hd(i)-qd(i)=1时,删除qd(i)、hd(i)或qd(i)、hd(i-1)。交叠区间的优化,可有效减少因骨架提取缺陷所产生的伪交叠区间以及合并被分割的交叠区间,能够提高算法运行速度,减少计算量。 步骤 4曲线估计。依次提取每列数据,当在非交叠区间内,转至步骤5;当在交叠区间内,转至步骤6;当分离最后一条曲线时,转至步骤7。 步骤 5非交叠区间曲线估计 (1) 当i-ii+1=2时 (13) (2) 当3≤i-ii+1 (14) (3) 当i0≤i-ii+1≤Na时 (15) 步骤 6交叠区间曲线估计 (16) 式中:{A|B}表示在满足B的条件下进行A操作。 (17) 交叠区间内的值为 (18) 步骤 7最后一条曲线估计。若qd(jj) 步骤 8清除当前曲线,返回步骤4。 具体流程图如图4所示。 图4 曲线估计与分离过程Fig.4 Curve estimation and separation process 相比于传统m-D曲线分离方法,本文所提方法利用骨架提取方法及交叠区间附近的曲线趋势,避免了诸如峰值法在交叠处的非首条曲线能量急剧减少导致分离错误的问题、最近邻原则法在交叠严重处极易错误估计的问题以及Viterbi算法在交叠处不具备有效区分度的问题等。 为更加直观地说明算法的有效性,对信号x1(t)及信号x2(t)进行曲线分离。其中,信号x1(t)组成分量如第2节开头所述,信号x2(t)由一个线性分量加两种不同频率的正弦分量组成,分离结果如图5所示。可以发现,本文算法对两种信号的分离效果均很好,有效解决了曲线交叠问题。 图5 两种示例信号的分离效果Fig.5 Separation effect of two sample signals 非平稳信号由多个单分量信号组成,研究非平稳信号的组成单分量十分有必要。VMD不同于传统模态分解方法的递归模式,其将信号的分解过程转化到了变分模式中,主要过程是将一个非平稳信号分解为指定个数的相互独立的模态uk中,每个模态对应一个中心频率wk。除此之外,为使分解出的各分量的带宽之和最小,需要通过希尔伯特变换计算出每个模态的单边频谱,再根据各自的中心频率得到各模态的基带信号,最后根据高斯平滑统计各个模态带宽之和: (19) 式中:{uk}={u1,u2,…,uk}为所有模态的集合;{wk}={w1,w2,…,wk}为所有模态中心频率的集合;∂t表示对t求偏导。 通过引入二次惩罚项和拉格朗日乘子将问题转化为无约束问题,式(19)将转化为增广拉格朗日形式: (20) 式中:N是期望分解出的模态数量;β是惩罚因子;λ是拉格朗日乘子。在频域中使用交替方向乘子法,得出u,w,λ在频域的更新公式: (21) (22) (23) 合理设置参数N,β,λ,最大程度上对非平稳信号进行分解,得出本征模态函数(intrinsic mode function,IMF)。 设共有4个目标,各自属性如表1所示,当目标为锥形结构时,以锥鼻以及一对对称的锥尾边缘散射点构建目标散射点模型;当目标为杆状结构时,以两端散射点构建目标模型。 表1 目标基本属性 不考虑目标的平动,雷达发射信号为脉冲体制的线性调频信号,脉冲宽度为10 μs,脉冲重复频率为200 Hz,载频为9 GHz,带宽为2 GHz。各目标散射点散射强度为[0,1]中的随机值。 通过第2节和第3节所述方法,4个目标对应的m-D曲线均能实现较好的分离,且能正确提取出目标的微动特征,能有效验证本文所提算法。由于篇幅的限制,现选择目标3和目标4进行结果展示及详细分析。图6是目标3在f-tm平面上的m -D曲线。对图6中曲线进行二值化,再利用1×1像素的高斯空间掩膜对其进行高斯平滑处理,通过骨架提取算法得到图7所示图像。设置曲线分离参数i0=15,ε=9,ΔmD=4,得到分离结果,并与峰值法、最近邻原则法及Viterbi算法进行比较,结果如图8所示。 图6 原始m-D曲线(目标3)Fig.6 Original m-D curve (target 3) 图7 二值化及骨架提取得到的m-D曲线(目标3)Fig.7 m-D curve obtained by binarization and skeleton extraction (target 3) 图8 传统算法与本文算法的分离效果(目标3)Fig.8 Separation effect by traditional algorithms and proposed algorithm (target 3) 观察图8可以发现,峰值法对能量依赖较大,当待分离曲线的能量差别较小时,会出现图8(a)所示的结果;最近邻原则法在曲线交叠处基本无效;Viterbi算法在两交叠点之间曲线路径相差较小的情况下易出现错误分离现象;而本文算法在分离较为复杂的交叠曲线时能够取得较好的效果。 利用本文算法分离出的m-D曲线,分别采用EMD和VMD算法,合理设置参数,得到该目标m-D曲线的分解结果如图9所示。 图9 目标3 m-D曲线EMD及VMD分解结果Fig.9 M-D curve EMD and VMD decomposition results of target 3 目标3为杆状目标,两端点处散射点的m-D特性基本上一致。杆状结构目标自旋轴是自身,故微动只需考虑进动和章动,根据表1及理论算法,应当分解出1.0 Hz,1.6 Hz,2.6 Hz,3.6 Hz 4种频率分量。观察图9发现,采用EMD分解,混叠现象严重,很难观察到各单频模态;而采用VMD分解则可分解出1.6 Hz,2.6 Hz,3.6 Hz 3种分量。分析EMD分解结果,无法确定目标的进动和章动频率;而分析VMD分解结果,最高频应是进动与章动频率之和,为3.6 Hz,则1.6 Hz及2.6 Hz中必有一个是进动或章动频率,若是1.6 Hz,另一频率应为2.0 Hz,不可能出现2.6 Hz这一分量,从而分析出进动和章动频率分别为1.0 Hz和2.6 Hz。 目标4为锥体目标,不同于杆状目标,散射点模型组成有锥鼻和锥尾边缘之分。按照本文所提分离算法对目标4的m-D曲线进行分离,并与传统m-D曲线分离算法进行比较,得到如图10~图12所示曲线分离结果。观察图12同样可以发现本文算法与传统算法的区别,在m-D曲线交叠处,传统算法极易出现错误匹配现象,导致分离结果出错;而本文算法则能正确分离出交叠的曲线,方便后续微动特征的提取。 图10 原始 m-D曲线(目标4)Fig.10 Original m-D curve (target 4) 图11 二值化及骨架提取得到的m-D曲线(目标4)Fig.11 m-D curve obtained by binarization and skeleton extraction (target 4) 图12 传统算法与本文算法的分离结果(目标4)Fig.12 Separation effect by traditional algorithms and proposed algorithm (target 4) 利用VMD及EMD算法对分离出的锥鼻及锥尾边缘散射点的m-D曲线进行分解,得如图13和图14所示结果。 图13 目标4锥鼻散射点m-D曲线EMD及VMD分解结果Fig.13 m-D curves EMD and VMD decomposition results of cone-nose scatterer of target 4 结合表1,若所有散射点均存在自旋、进动和章动3种微动,则目标4每个散射点的m-D曲线理论上可分解出0.2 Hz,1.2 Hz,1.4 Hz,1.6Hz,2.6 Hz,2.8 Hz,3.0 Hz,4.0 Hz,4.2 Hz,5.4 Hz 10种模态。但锥鼻处散射点在其自旋轴上,可不考虑自旋对其影响,其m-D曲线应分解出1.4Hz,2.8 Hz,4.2 Hz 3种模态。观察图13可以发现,锥鼻散射点m-D曲线EMD分解可勉强分解出1.4 Hz,其他模态均混叠严重。相较而言,VMD分解能够很好地分解出1.4 Hz,2.8 Hz,4.2 Hz 3种模态。根据VMD分解结果,可计算出目标4的进动和章动频率分别为1.4 Hz和2.8 Hz。再观察图15,发现EMD分解结果混叠严重,VMD算法可分解出1.2 Hz,1.6 Hz,2.6Hz,3.0 Hz,4.0 Hz,4.2 Hz,5.4 Hz 7种清晰模态,结合之前计算出的目标的进动和章动频率,可以很快计算出目标的自旋频率为1.2 Hz。 观察目标3和目标4的EMD及VMD分解结果,可以发现无论是EMD还是VMD分解,都无法完全分解出所有的变量,原因可能如下:① VMD算法自身存在低频分量无法分解的问题;② 组成各m-D曲线的模态较为接近,VMD分解过程中可能将相近的模态合并;③ 曲线分离过程中,交叉区域使用线性插值估计中间值与原始值存在偏差,导致提取出的m-D曲线存在误差,从而遗失部分分量。 为了更好地体现曲线分离过程中产生的误差,以目标4的分离结果进行误差分析,结果如图15和图16所示。 图15 曲线分离结果与原始图比较Fig.15 Comparison of curve separation results with original graph 观察图15可以发现,本文提出的曲线分离方法得出的曲线在极值处与原始曲线存在一定的误差,图16所示结果也很好地显示出了这一现象。但观察图16可以发现,本文所提曲线分离方法误差基本在[-1.5,1]区间内,属于正常范围,因此本文所提方法能有效实现曲线分离。 图16 误差曲线Fig.16 Error curve 为了进一步测试算法稳定性和计算时间复杂度,对比分析各算法在不同信噪比下的均方根误差及运行时间。如图17所示,在信噪比高于-15 dB时,本文算法均能有效分离不同目标的m-D曲线。这说明此时算法对信噪比不敏感,其原因是本文算法的曲线分离过程是基于骨架提取进行的,当信噪比高于-15 dB时,本文所提方法均能完整地提取目标m-D曲线骨架;但是当信噪比低于-15 dB后,由于骨架提取出现大量断点,导致后续分离过程产生伪交叠区间,进而无法有效分离m-D曲线。反观另外几种分离算法,可以发现,Viterbi算法在信噪比大于0 dB时,均方根误差急剧减小,但仍比本文算法大;最近邻原则法前期处理同样需要提取m-D曲线骨架,对信噪比敏感性也不高,但均方根误差极大,表明分离错误率较高;峰值法均方根误差浮动较大,对曲线能量的要求极高,不适用于各m-D曲线能量相近的情况。 图17 信噪比分析Fig.17 Signal to noise ratio analysis 算法计算时间复杂度方面,对每种算法进行500次蒙特卡罗实验,平均运行时间如表2所示。仿真平台为64位Windows 10操作系统,内存16 GB,AMD处理器,内核Ryzen 7 4800H,CPU 2.9 GHz,MATLAB R2018b。对比表2所示各种算法的运行时间可以发现,本文算法快于Viterbi算法,慢于最近邻原则法及峰值法。然而,结合图18信噪比分析结果,本文算法在稳定性和实时性方面的几种算法中是最优的。 表2 算法时间复杂度 本文针对章动目标,通过等效散射点模型及回波模型获得回波信号及m-D曲线。针对m-D曲线交叠和分离问题,提出一种基于曲线趋势估计的分离算法。经实验验证,所提方法可有效解决曲线交叠问题,正确分离m-D曲线。然后,利用VMD算法对分解出的每一条m-D曲线进行分解,将分解结果与EMD分解结果进行对比,发现VMD算法分解效果更佳,混叠程度更低,更加有利于获得目标的自旋、进动及章动频率。最后,通过信噪比及时间复杂度分析,发现算法能在信噪比高于-15 dB时实现m-D曲线的快速稳定有效分离。
n=m+1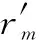
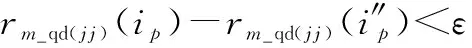
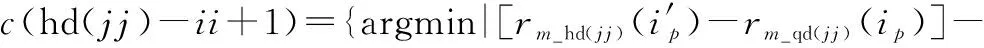
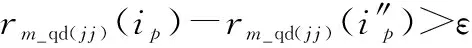
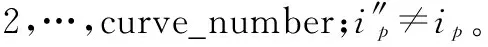
3 基于VMD算法的微动分量提取
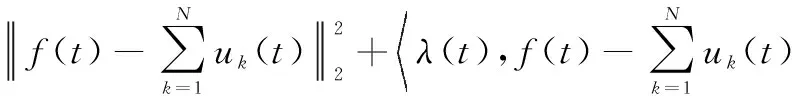
4 仿真分析



5 结 论

