基于Hilbert-Huang变换与对抗训练的特定辐射源识别

谢存祥, 张立民, 钟兆根

(1. 海军航空大学信息融合研究所, 山东 烟台 264001;2. 海军航空大学航空基础学院, 山东 烟台 264001)

0 引 言

随着现代战争形态向着信息化发展,电子战在信息化战争发挥着越来越重要的作用。其中,特定辐射源识别是电子战,特别是非合作通信下通信侦察中的一项关键技术,主要根据截获的射频通信信号的细微差异判断所属辐射源[1],根据辐射源工作状态掌握对方装备载体的情况,从而有针对性地进行监视、干扰及打击[2-4]。

目前,国内外针对辐射源识别问题,主要针对暂态信号与稳态信号两类信号进行研究。暂态信号是指辐射源在开、关机时由于工作状态不稳定所产生的能体现辐射源特征的信号[5],因其持续时间短且受噪声干扰影响大,不易于进行辐射源识别。稳态信号是指辐射源稳定工作时所辐射的信号,易获取且受噪声干扰影响相对较小,因此是辐射源识别的研究重点[6-7]。

近年来,众多学者针对稳态信号提出多种处理方法,主要包括时频分析[8-9]、高阶谱分析[10]、Hilbert-Huang变换[11-13]等。文献[8]提出了二次时频分布与顺序分类器的特定辐射源识别方法,可以实现辐射源的在线学习与识别。但二次时频分布存在交叉项影响,对识别会产生较大影响。文献[9]提出采用短时傅里叶变换的方法进行辐射源识别,但此方法是基于线性变换,对于非线性的辐射源信号适用性不强,识别效果不佳。文献[10]通过积分双谱结合流形学习的方法对辐射源信号进行特征提取,进而实现辐射源个体识别。但高阶谱分析的方法仅能提取辐射源信号的部分特征,会丢失部分重要的细微特征,影响识别效果。Hilbert-Huang变换非常适用于处理非平稳、非线性的辐射源信号[14],文献[11-12]通过对辐射源信号进行Hilbert-Huang变换得到Hilbert谱,然后通过二阶矩算法提取Hilbert谱的一阶矩、二阶矩以及能量熵,作为指纹特征区分不同辐射源。文献[13]在此基础上,进一步采用Hilbert谱平坦度、Hilbert谱亮度以及Hilbert谱滚降作为指纹特征,提高了辐射源识别精度。

传统的特定辐射源识别技术一般是根据预先设定的特征参数模型,对辐射源信号提取特征参数,进而识别不同辐射源[15-17]。但辐射源信号的复杂性至今无法用统一的数学模型表示,传统方法提取的特征参数无法全面表征辐射源特征,识别性能提升有限。随着人工智能技术的发展,深度学习开始应用于特定辐射源识别中,通过神经网络能全面地、深层次地提取辐射源信号的特征,提升识别性能,是一个全新的研究方向。文献[18]针对7台ZigBee设备,通过卷积神经网络对原始的时域基带信号进行特征提取,达到了92.29%的识别精度。文献[19]通过卷积神经网络对辐射源信号的积分双谱进行处理,提取了隐藏在原始信号中的整体特征信息，并通过实验证明了这种方法优于传统的基于手工提取特征的方法。文献[20]针对文献[19]中积分双谱会导致信号特征部分损失的问题,采用残差神经网络对信号经过Hilbert-Huang变换后得到的Hilbert谱的灰度图进行处理,并通过实验论证了算法的优越性。

现有的基于深度学习的特定辐射源个体识别方法一般预处理的程度不够,将较为原始的信号数据直接送入神经网络进行训练,这会带来大量冗余数据,增大网络训练与识别计算量的同时也会影响神经网络对深层特征的挖掘。另外,神经网络一般采用未经抗噪处理的卷积神经网络,在处理噪声影响下的辐射源信号时会增加误识别的可能。因此,本文综合现有文献的方法与成果,在对辐射源信号进行Hilbert-Huang变换得到Hilbert谱的基础上,增加预处理环节,选出不同信号Hilbert谱上最具区分度的能量值点,然后采用对抗训练的方式提升卷积神经网络的抗噪性能。仿真实验分别从识别准确率、算法鲁棒性以及计算复杂度3个方面验证算法的性能。

1 信号模型

假设理想状态下通信辐射源发出的带通信号x(t)可表示为

x(t)=Re[xl(t)ej2πf0t]

(1)

式中:f0为载频频率；xl(t)=xi(t)+jxq(t)是x(t)的低通等效信号,且为基带已调信号,xi(t)与xq(t)分别为x(t)的同相与正交分量。

因此式(1)可表示为

x(t)=xi(t)cos(2πf0t)-xq(t)sin(2πf0t)

(2)

实际情况中,由于受生产工艺、安装调试等现实因素影响,必然导致辐射源的内部元器件(本地振荡器、混频器、功率放大器等)工作处于不理想状态,进而导致在调制过程中对于同相分量与正交分量会引入幅度偏差与相位偏差,这种偏差对于不同辐射源是特异的,因此可以作为识别不同辐射源的基础[21]。信号模型可表示为

x(t)=(1+α)xi(t)·
cos(2πf0t+θ)-xq(t)sin(2πf0t)+n(t)

(3)

式中:α为幅度偏差；θ为相位偏差；n(t)为高斯白噪声。不失一般性,假设幅度偏差与相位偏差均在同相分量上。对于不同的辐射源,幅度偏差与相位偏差的组合(α,θ)不同。

2 基于Hilbert-Huang变换的辐射源信号预处理

Hilbert-Huang变换是处理非线性与非平稳信号的有力工具,包括经验模态分解(empirical mode decomposition, EMD)与Hilbert谱分析(Hilbert spectral analysis, HSA)。EMD基于信号本身的局部性质,可将复杂信号分解为有限个简单的固有模态函数(intrinsic mode function, IMF),通过对分解得到的固有模态函数进行Hilbert变换,可以得到以时间为自变量的瞬时频率,进而得到Hilbert时频能量谱。不同辐射源发出的信号的差异可通过Hilbert谱很好地体现出来[14]。

2.1 经验模态分解与Hilbert谱分析

EMD的本质是一个筛选过程,假设x(t)为原始信号,具体步骤如下[22-23]。

步骤 1通过拟合分别确定由局部最大值点与局部最小值点产生的上包络u(t)和下包络l(t),其均值为m1(t)=[u(t)+l(t)]/2,并令:

h10(t)=x(t)-m1(t)

(4)

步骤 2对于h10(t),同样通过拟合分别确定由局部最大值点与局部最小值点产生的上包络u11(t)和下包络l11(t),其均值为m11(t)=[u11(t)+l11(t)]/2,并令:

h11(t)=h10(t)-m11(t)

(5)

步骤 3重复步骤2,通过k次迭代得到:

h1k(t)=h1(k-1)(t)-m1k(t)

(6)

直到满足:

(7)

式中:T为信号长度；ε为设定阈值,一般参考范围为:0.2～0.3。此时

c1(t)=h1k(t)

(8)

为筛选得到的第一个IMF分量。

步骤 4令

r1(t)=x(t)-c1(t)

(9)

对于r1(t),重复步骤2和步骤3得到:

(10)

上述迭代过程直到rm(t)的极值点个数小于等于1(不存在振荡波形)时停止。此时

(11)

即x(t)分解为c1(t),c2(t),…,cm(t)的m个IFM分量以及余项rm(t)。

对于实际信号x(t),其EMD过程的结果如图1所示。

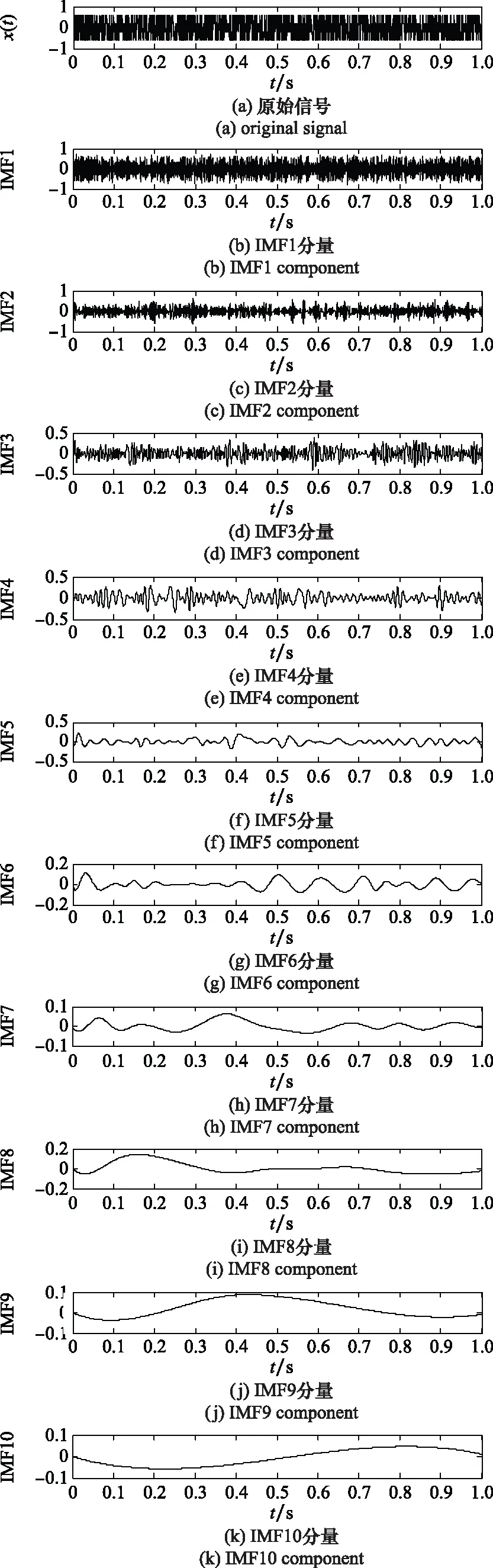
对分解得到的IFM分量ck(t)进行Hilbert变换,得到:

(12)

令

(13)

式中:ak(t)、θk(t)和ωk(t)分别为ck(t)的瞬时幅度、瞬时相位和瞬时频率,由此得到信号的Hilbert谱H(t,ω)为

(14)

根据第1节的信号模型,构建两类不同信号x1(t)和x2(t),其Hilbert谱仿真图如图2所示。

图2 两类不同信号的Hilbert谱Fig.2 Hilbert spectrum of two different signals

图2采用灰度图的方式显示信号的Hilbert谱,不同时频点的相对能量值通过灰度表示。图2(a)与图2(b)为不同类信号的Hilbert谱,从直观上看存在一定差异,因此可作为辐射源识别的一种方法。

2.2 基于Hilbert谱的预处理

对于不同辐射源信号的Hilbert时频能量谱,只有一部分时频点对应的能量值存在良好的区分特性,其他的时频点特征性不强,对于辐射源的识别起到的作用不大,甚至会产生反作用。因此，需要将具有良好区分特征的时频点提取出来作为特征量,从而保证辐射源识别过程中类间差异最大、类内差异最小。特征时频点的提取算法[24]如下。

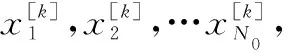
(2) 对于K类信号的Hilbert谱的所有时频点{(t1,ω1),(t2,ω2),…,(tNH,ωNH)},计算每一点对应的区分度为

(15)

式中:Ei[·]表示第k类信号的Hilbert谱H[k](t,ω)对应的N0个样本的均值;Di[·]表示第k类信号的Hilbert谱H[k](t,ω)对应的N0个样本的方差。分母项表示同一信号的Hilbert谱H(t,ω)在某一时频点(t,ω)的稳定程度,其值越小表示类内差异越小;分子项表示不同信号的Hilbert谱H(t,ω)在某一时频点(t,ω)的差异程度,其值越大表示类间差异越大。

(3)K类信号Hilbert谱的时频点的区分度组成集合Ω={F(t1,ω1),F(t2,ω2),…,F(tNH,ωNH)},其中F(t1,ω1)≥F(t2,ω2)≥…≥F(tNH,ωNH),选取前ND个时频点{(t1,ω1),(t2,ω2),…,(tND,ωND)}所对应的Hilbert谱能量值,用于对K类辐射源进行分类。

ND的选取要从区分能力与计算量两方面考虑。区分能力方面,选取区分度排名前ND的时频点对应的Hilbert谱能量值,要对K类辐射源信号有足够高的区分能力;计算量方面,在保证区分能力的基础上,ND要尽可能少,以减少后续神经网络在训练与识别过程中的运算量,提升系统效率。一般而言,ND通常选取全部时频点个数的前1%～10%,然后在此范围内通过实验确定ND。

3 卷积神经网络与对抗训练

3.1 卷积神经网络

信号经过第2节处理后得到的数据,送入卷积神经网络进行特征提取与分类从而实现辐射源识别的任务。

假设存在K个待识别的辐射源,辐射源信号通过Hilbert-Huang变换后得到的Hilbert能量谱尺,然后根据第2.2节的Hilbert谱预处理算法,提取Hilbert谱中最具区分度的前ND个时频点对应的能量值,作为卷积神经网络的输入向量。本文卷积神经网络的构架如图3所示。

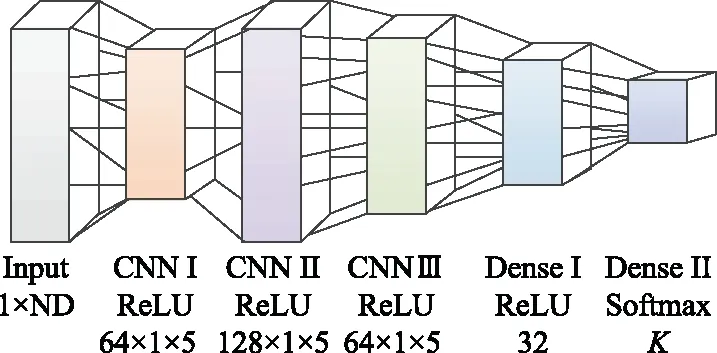
图3 卷积神经网络架构Fig.3 Convolutional neural network architecture

图3所示卷积神经网络中,因为要将ND个时频点对应的能量值送入卷积神经网络,因此卷积神经网络的输入层尺寸为1×ND。卷积层主要是对输入向量进行特征提取。卷积层包含多个卷积核,分别对前一层的特征图进行卷积,从而实现多特征提取。卷积层Ⅰ包含64个卷积核,卷积核尺寸为1×5;卷积层Ⅱ包含128个卷积核,卷积核尺寸为1×5;卷积层Ⅲ包含64个卷积核,卷积核尺寸为1×5。这里卷积核的深度均为1。卷积层的激活函数统一采用ReLU函数,目的是为卷积层引入非线性因素,避免成为输入向量的线性组合,从而能够提取复杂且深层次的特征。卷积层提取的特征图通过全连接层进行向量化,从而将分布式特征表现映射到样本的标记空间。卷积层Ⅲ的输出为1×5×64的特征图(尺寸为1×5,深度为64),而全连接层Ⅰ包含32个神经元,因此全连接层Ⅰ的每一个神经元实质是尺寸为1×5×64的卷积核,通过全局卷积完成全连接层Ⅰ的运算。全连接层Ⅰ输出尺寸为1×32的一维向量，然后送入全连接层Ⅱ计算，并最终通过Softmax函数映射为输出概率。全连接层Ⅱ输出K个输出概率，对应于K个待识别辐射源的识别概率，选取输出概率最大所对应的辐射源即为识别结果。

3.2 对抗训练

现实情况中,不同辐射源的细微硬件差异导致其发射信号的幅度与相位偏差一般是不明显的,因此容易受到噪声干扰而出现误识别。以此本文在卷积神经网络的基础上采用对抗训练的方法来提升神经网络分类器的抗噪性能。

对抗训练的关键在于对抗样本的生成。对于一个训练好的用于分类的卷积神经网络,当输入向量x叠加一个细微扰动Δx后,网络损失值最大对应的Δx即为对抗样本。此时的细微扰动Δx最容易使得原神经网络出现误判,因此需要以输入向量x+Δx和真实标签ytrue对神经网络进行训练,提升神经网络识别对抗样本的性能,增强鲁棒性。

综上,对抗训练的数学模型[25]可表示为

(16)

式中:x为输入向量；y为标签；D为训练集；θ为神经网络参数；J(x,y;θ)为损失函数,这里采用交叉熵函数:

J(x,y;θ)=-ylnypre(x;θ)

(17)

式中:ypre(x;θ)表示将输入向量x送入参数为θ的神经网络模型中得到的预测向量。

根据梯度原理,最优的细微扰动Δx可通过下式构造:

(18)

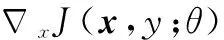
(19)

根据信号特征进行辐射源分类识别时,对于每一类辐射源的信号数据,其对抗样本的扰动加权系数ε都存在一个临界值ε*,该临界值是所有可导致误识别的ε中的最小值,此时对应的Δx即为可导致误识别的最细微的扰动,以此为对抗样本进行对抗训练，最大程度地提升神经网络的抗噪性能[26]。

上述生成对抗样本的算法具体如下。

步骤 1对于第k类辐射源信号,输入向量xk及对应的标签yk-true,计算其损失值的梯度(归一化):

(20)

步骤 2采用二分法确定扰动加权系数ε的临界值,设定初始扰动加权系数范围上限εmax=ε0,范围下限εmin=0,二分精度εacc。

步骤 3计算扰动加权系数的上下限平均值εave:

εave=(εmax+εmin)/2

(21)

以εave为扰动加权系数更新对抗样本:

(22)

(23)

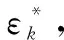
(24)

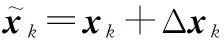
确定了所有类对抗样本之后,为保证神经网络结构不改变,将对抗样本产生的损失函数以正则化的形式加入原损失函数中:

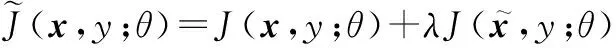
(25)

(26)

4 实验验证与分析

4.1 实验设置

信号按照式(3)所示模型通过Matlab仿真产生。根据文献[21],幅度偏差绝对值取值范围一般为0.2～0.82,相位偏差绝对值取值范围一般为2°～11.42°。据此,本文的信号模型中两者绝对值的取值范围分别设定为:0.2～0.8和2°～10°。信号调制类型统一采用16 QAM,载频频率f0=25 kHz,采样频率fs=100 kHz。

对于各类信号,信号样本采样点数为1 000,经过大量实验得到在不同信噪比下对其进行经验模态分解,一般会得到10个IMF分量(为了实验简便,对于个别经过经验模态分解得到的IMF分量不为10的信号,予以舍弃)。因此，总共的时频能量点个数为10 000。然后，根据第2.2节的预处理算法,确定具有区分度的时频点个数以及对应的能量值,将其作为信号特征参数送入卷积神经网络进行训练与识别。卷积神经网络架构如图3所示,网络在训练过程中通过对抗训练的方式提升其抗噪性能。

4.2 时频能量点个数确定

本节首先需要验证:只有一部分时频点对应的Hilbert谱能量值具有良好的区分特性,其他的时频点特征性不强,对于辐射源的识别起到的作用不大,甚至会产生反作用。即验证第2.2节提出的Hilbert谱预处理算法对于增强区分度和提升识别性能的意义。

根据第1节的信号模型,分别设置4类、5类、6类辐射源信号,信号的幅度与相位偏差如表1所示。

表1 辐射源个数分别为4、5、6时的信号幅度与相位偏差

为了更好地体现区分效果,在信噪比较低的10 dB环境下每一类辐射源信号产生1 000个样本,然后随机划分为训练样本(每类信号500个样本)与测试样本(每类信号500个样本)。对全部训练信号样本进行Hilbert-Huang变换得到Hilbert能量谱,然后通过Hilbert谱预处理算法将其时频能量点按照区分度由大到小的次序进行排序,并记录相应的时频坐标信息。

在验证过程中,对于训练集与测试集中的信号样本所对应的Hilbert能量谱,根据区分度的排序以及对应的时频坐标信息,分别选取排名前500、1 000、…、10 000范围内的时频点对应的能量值作为信号的特征参数,送入卷积神经网络进行训练与测试,其中训练方式为对抗训练。对于全部的时频能量点，不同的区分度排名范围对应的识别率曲线如图4所示。

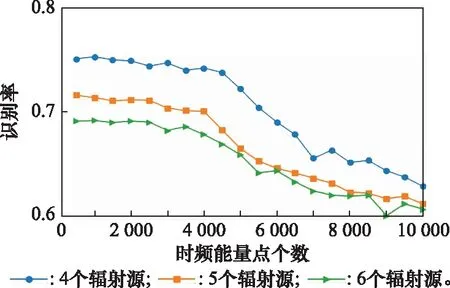
图4 不同的区分度排名范围对应的识别率曲线Fig.4 Identification accuracy curves corresponding to different discrimination ranking ranges

由图4可得,当选取区分度排名在1～1 000范围内的时频能量点作为信号的特征参数时,对不同个数的待识别辐射源进行识别,识别率均保持在较高水平。在此基础上增加区分度排名在1 000～4 500范围内的时频能量点时,识别率略有下降但基本保持不变。最后，引入区分度排名在4 500～10 000范围内的时频能量点,识别率明显出现下降趋势。实验结果表明,只采用区分度高的时频能量点进行辐射源个体识别时识别效果最佳,在此基础上增加区分度一般的时频能量点用于识别,对提升识别效果帮助不大。最后，随着区分度较差的时频能量点的引入,识别率开始降低,说明这些时频能量点对识别性能起到了反作用。因此，论证了Hilbert谱预处理算法的可行性与优越性。

在此基础上确定时频能量点个数。由于上述实验证明了当选取区分度排名在1～1 000范围内的时频能量点作为信号的特征参数时,识别效果最佳。因此，在这一范围内分别选取区分度排名前100、200、…、1 000范围内的时频能量点作为辐射源分类的特征参数,通过对抗训练的方法训练卷积神经网络用于辐射源个体识别。不同的区分度排名范围对应的识别率曲线如图5所示。

由图5可得,对于区分度排名前1 000的时频能量点,识别率基本均保持不变。考虑到时频能量点个数较多会增加卷积神经网络在训练与识别过程中的计算量,影响系统的效率,因此需要选取尽可能少的时频能量点个数。所以最终选取区分度排名前100的Hilbert谱时频能量点作为辐射源信号的特征参数,用于卷积神经网络的训练与识别。

图5 不同的区分度排名范围对应的识别率曲线(对于区分度排名前1 000的时频能量点)Fig.5 Identification accuracy curves corresponding to different discrimination ranking ranges (for the top 1 000 time-frequency energy points with discrimination)

4.3 识别准确率验证

实验 1不同信噪比下识别准确率测试

本节设置待识别辐射源的个数为4个,根据表1所示的信号幅度与相位偏差生成每一类辐射源信号样本1 000个,并随机划分为训练样本(每类信号500个样本)与测试样本(每类信号500个样本),然后加入高斯白噪声并设置信噪比范围10～20 dB,间隔2 dB。

对于不同信噪比下所有训练样本,首先进行Hilbert-Huang变换得到Hilbert能量谱,然后通过Hilbert谱预处理算法获得Hilbert能量谱上区分度排名前100的时频能量点,并记录相应的时频坐标信息。对于不同信噪比下的训练集与测试集中的信号样本所对应的Hilbert能量谱,根据之前记录的时频坐标信息提取相应的能量值,以此作为信号特征参数送入卷积神经网络进行训练与测试,训练方式为对抗训练。最后测试不同信噪比下的辐射源个体识别率。

同时,为了凸显本文算法的优势,采用另外两种算法与之对比:① 不采用对抗训练的方法,仅通过常规训练方式训练卷积神经网络,以此进行辐射源个体识别;② 不采用预处理算法,将信号的Hilbert谱的全部时频能量值作为卷积神经网络的输入,同时不采用对抗训练的方法,仅通过常规训练方式训练卷积神经网络,以此进行辐射源个体识别。

当信噪比分别为10 dB、16 dB、20 dB时,采用本文算法进行辐射源个体识别得到的混淆矩阵如图6所示。另外,采用本文算法以及两种对比算法进行辐射源个体识别,在不同信噪比下的识别率数值以及识别率曲线分别如表2和图7所示。其中,“M1”表示本文方法,“M2”表示不进行对抗训练的方法,“M3”表示不进行预处理与对抗训练的方法,下同。

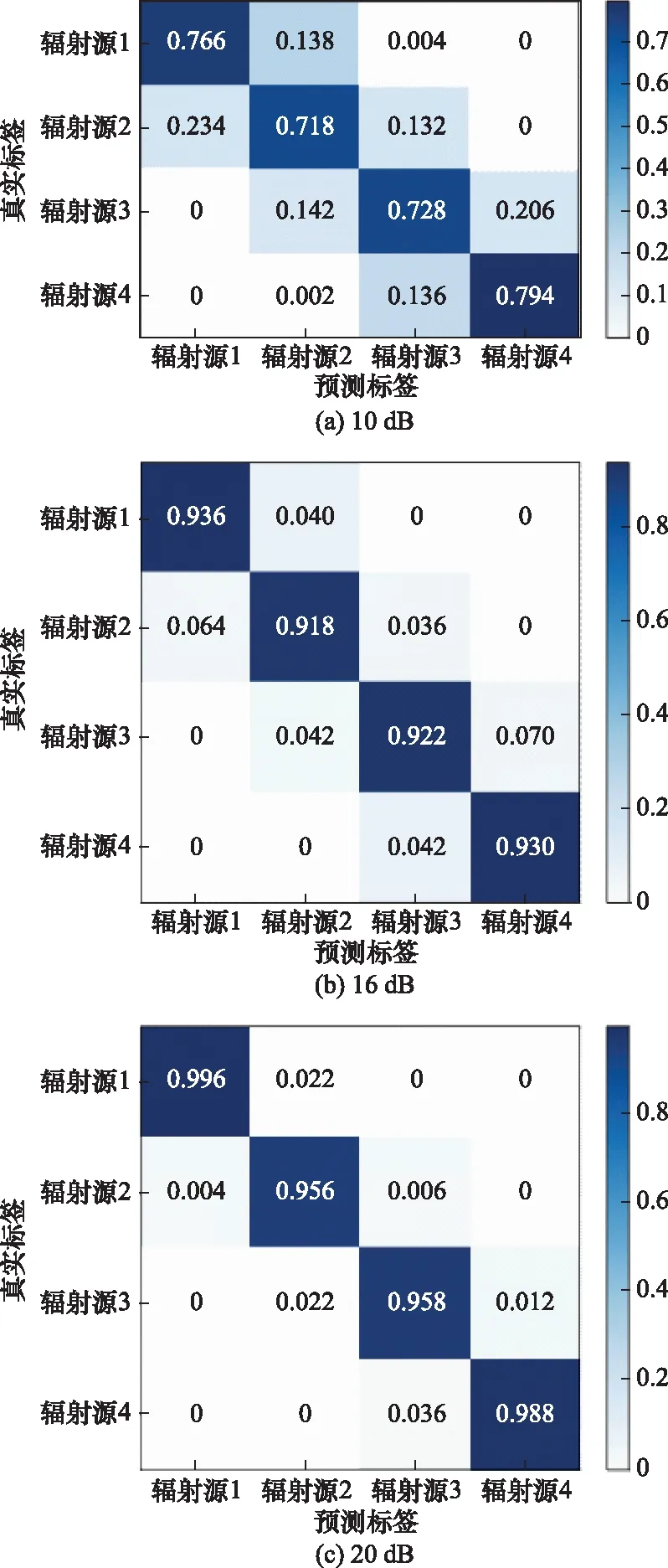
图6 不同信噪比下信号识别混淆矩阵Fig.6 Confusion matrix of signal identification at different signal to noise ratios

表2 辐射源个数为4时不同方法识别率数值

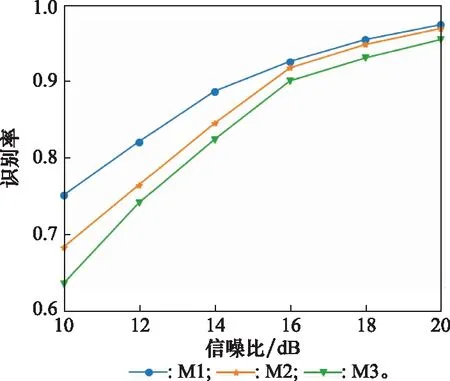
图7 不同方法的辐射源识别率曲线Fig.7 Emitter identification accuracy curves of different methods

由图6和图7可得,在不同信噪比下,不同辐射源识别率基本保持相同,这是由于幅度与相位偏差等距选取所导致。同时，误识别基本发生在幅度与相位偏差临近的辐射源中。

由表2与图7可得,对比不进行对抗训练的方法,本文方法识别率平均提升3.1%。在低信噪比下两种方法的识别率相差较大;在中间信噪比范围内,本文方法相比不进行对抗训练的方法识别率也有一定程度的提升;只有在高信噪比下两者的识别率才大致相同。这说明对抗训练的方法能一定程度提升神经网络的抗噪性能,只有在信噪比较高(大于16 dB)时,因为信号质量较好,对抗训练与不进行对抗训练的识别效果才会相同。对比不进行预处理与对抗训练的方法,经过预处理但未进行对抗训练的方法识别率平均提升2.35%,本文算法识别率平均提升5.45%。这是因为通过预处理舍弃了区分度不大甚至会起到负面区分效果的能量点,一定程度增加了不同辐射源信号之间的类间差异性以及类内聚集度。

4.4 识别鲁棒性验证

本节鲁棒性验证包括两个方面:① 改变训练样本数,测试本文算法在不同信噪比下的识别率;② 改变辐射源个数,测试本文算法在不同信噪比下的识别率。

实验 2训练样本数对识别准确率的影响

辐射源个数设置为4个,按照表1所示的信号幅度与相位偏差设置每一类辐射源信号样本,并随机划分为训练样本与测试样本。训练集中,每一类信号的样本数分别取100、200、300、400、500;测试集中,每一类信号的样本数固定为500。最后，对不同数目的训练样本,按照实验1的实验过程,在不同信噪比下(10～20 dB,间隔2 dB)测试识别率,识别率数值以及识别率曲线分别如表3和图8所示。

表3 训练样本数分别为100、200、300、400、500时辐射源识别率数值

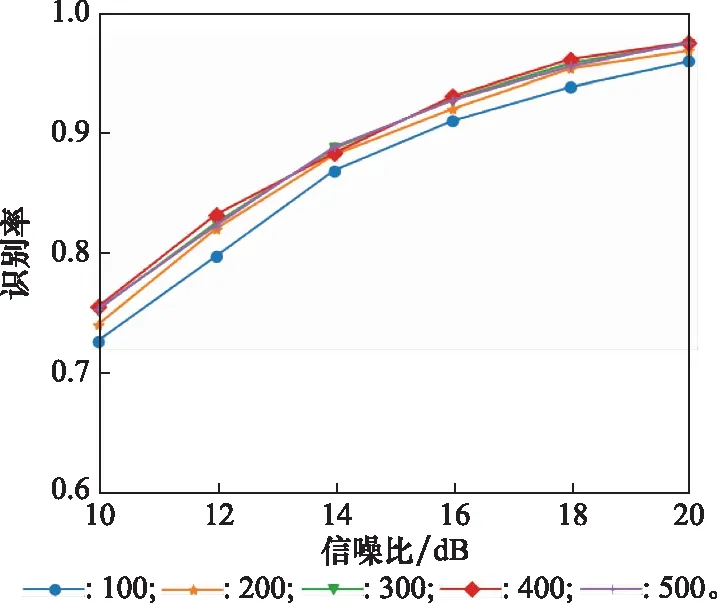
图8 不同训练样本数下辐射源识别率曲线Fig.8 Emitter identification accuracy curves under different number of training samples

由图8可得,网络的识别性能基本不随训练样本个数的变化而变化,在训练样本为100时的“小样本”条件下依旧可保持较高识别率。因此,本文算法不需获取大量数据样本进行训练即可达到较好的识别性能,这一定程度上可以弥补在非合作通信环境下无法获得大量样本数据的弊端,在小样本条件下即可实现较好的识别性能。

实验 3辐射源个数对识别准确率的影响

辐射源个数分别取5和6,根据表1所示的信号幅度与相位偏差生成每一类辐射源信号样本1 000个,并随机划分为训练样本(500个信号样本)与测试样本(500个信号样本)。然后，加入高斯白噪声并设置信噪比范围为10～20 dB,间隔2 dB。最后，对于不同的辐射源个数,按照实验1的实验过程进行辐射源个体识别。识别率数值如表4所示,识别率曲线如图9所示。

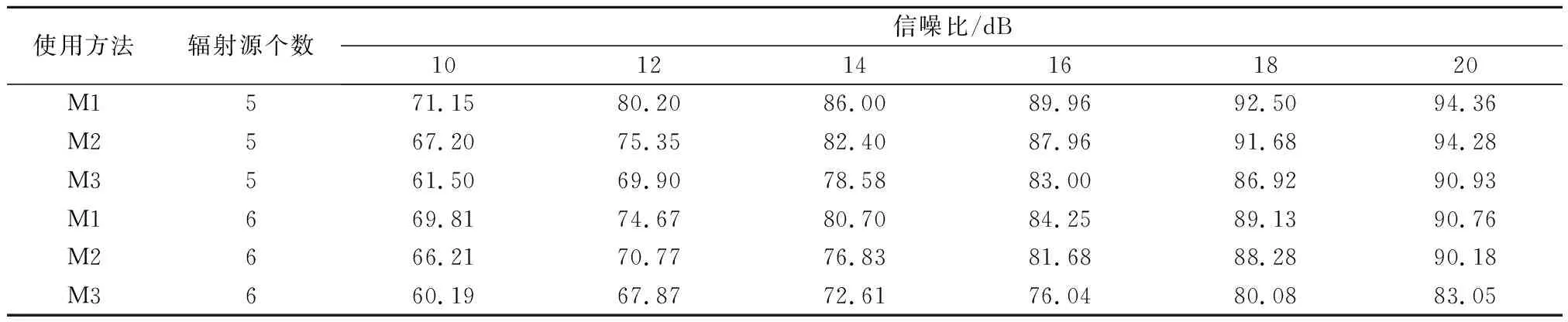
表4 辐射源个数分别为5和6时不同方法识别率数值

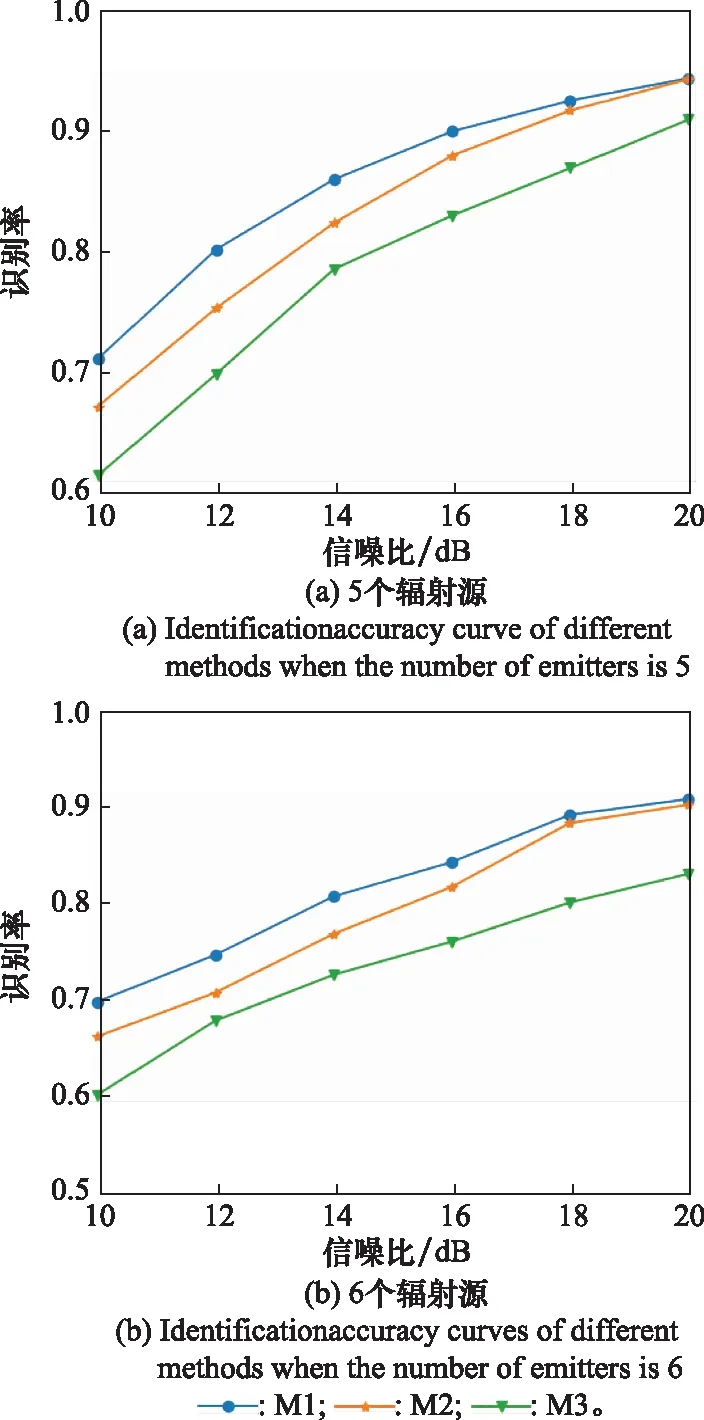
图9 辐射源个数分别为5和6时不同方法下的识别率曲线Fig.9 Identification accuracy curves of different methods when the number of emitters is 5 and 6 respectively

由表4与图9可得,随着辐射源个数的增多,本文算法识别率虽有下降,但下降不明显,在20 dB信噪比仍能保持90%以上的识别率。同时,相比不进行对抗训练,以及不进行预处理与对抗训练的方法,当辐射源个数为5时,本文算法识别率平均分别提升2.55%和7.20%;当辐射源个数为6时,本文算法识别率平均分别提升2.56%和8.20%。由此可得出本文算法随着辐射源个数增多,识别性能优势更加明显。

4.5 算法复杂度分析

本文算法复杂度分析主要包括经验模态分解与Hilbert谱预处理两部分。

对于经验模态分解,算法复杂度可大致表示为O(MNL+MNlogL+NLlogL),其中M表示得到一个IMF分量的迭代次数,N表示对信号筛选得到的IMF分量的个数,M和N一般为数值较小的整数值,本节分析中统一取M=N=10。L表示信号的采样点长度,本节取L=1 000。对于Hilbert谱预处理,设NH为Hilbert谱图的时频点数,NS为训练样本个数,K为辐射源个数。根据式(15)进行复杂度分析,由于均值与方差的复杂度均可表示为O(NS),分子计算次数为(K(K-1))/2,分母计算次数为K,因此式(15)复杂度为O((K2+K)NHNS/2)。

综上,本文算法在训练过程中复杂度可表示为O(MNL+MNlogL+NLlogL+(K2+K)NHNS/2)。

固定辐射源个数K=4,训练样本数Ns=500,当NH变化范围为104～106,算法复杂度在107～109范围内,属于可接受范围。

另外,本文算法的复杂度集中在预处理阶段,经过预处理确定最具有区分度的ND(通常ND取NH的1%～2%)个时频点后,在后续的神经网络进行大量训练与识别过程中,仅需对信号进行Hilbert-Huang变换得到Hilbert谱,并提取ND个特定时频点的能量值送入神经网络进行训练与识别,可较大程度降低运算量,能够满足系统实时性处理与识别的要求。

5 结 论

本文提出了一种基于Hilbert-Huang变换与对抗训练相结合的特定辐射源个体识别方法,通过对辐射源信号进行Hilbert-Huang变换得到Hilbert谱,然后通过预处理选择不同辐射源信号Hilbert谱中区分度最高的能量值点,将其送入卷积神经网络进行特征提取与分类识别,同时通过对抗训练提升卷积神经网络的抗噪性能。实验结果表明:本文算法在识别性能方面,对比不进行对抗训练,以及不进行预处理与对抗训练的方法,有不同程度提升;在识别鲁棒性方面,可以满足小样本条件下的识别,同时在辐射源个数增多的情况下,优势更加明显;在计算复杂度方面,虽然前期的预处理阶段会产生较大计算量,但在后期神经网络进行大量的训练与识别过程中,计算量会较大程度降低,能够满足系统实时性处理与识别的要求。在接下来的工作中,将会进一步改进算法,使其能够在复杂信道环境下(多径衰落、多普勒频移等)保持良好的识别性能。