基于贝叶斯算法的天线端到端优化

田春明, 杨 安, 叶 乐, 李建星, 贺雨晨

(1. 西安交通大学信息与通信工程学院, 陕西 西安 710049; 2. 北京大学微纳电子学系, 北京 100871;3. 西安交通大学电子科学与工程学院, 陕西 西安 710049)

0 引 言

随着天线的结构越来越复杂,需要优化的参数数量越来越多,快速有效的优化算法对天线设计至关重要。天线优化需要经过反复迭代的过程,受限于电磁仿真时间,实际的电磁仿真次数应尽可能少,以便快速实现优化目标。天线的优化可以被视为黑盒函数优化的问题,由于无法直接使用基于梯度下降的优化算法,进化算法(例如遗传算法、粒子群算法、模拟退火算法等)被广泛使用于天线设计[1-4]。由于进化算法需要大量的种群迭代,为了解决计算开销大的瓶颈,代理模型的方法被用于此类优化问题[5]。代理模型基于已采样数据,对被代理的函数做出拟合,能够显著减小计算量。近年来,建立在代理模型基础上的天线优化方法已成为趋势[6-16]。代理的数学模型有高斯过程(在地质统计学中被称为Kriging)[6-13]、支持向量回归[6]、神经网络[14-15]等。代理模型结合进化算法的方法日益广泛地应用于天线设计[8-9,11-12,16]。

在很多公开文献中,代理模型分别建立在目标频段范围内多个频点上[8-9],然后综合这些频点的拟合值进一步构建目标函数。在天线设计中,通常需要在一些限制条件下优化多个目标。对于这样的优化问题,已有的大部分文献提出了使用多目标优化的算法[8-12]:在代理的基础上通过迭代找到帕累托前沿;进一步地,可以在帕累托前沿中使用一个度量筛选出最佳天线参数组合。但是,在多目标优化中需要为优化目标和限制条件分别建立代理模型,计算开销大。文献[17]提出了一种综合目标函数的建立方法,该目标函数由分别代表S11、方向图、增益、天线尺寸的分目标函数综合而成,在建立综合目标函数的基础上,使用进化算法,整个优化过程以端到端的方式解决。

由于天线优化通常建立在小数据集上,神经网络在小数据集上表现出过拟合;支持向量回归不能作出不确定性估计;而高斯过程可以基于样本集估计出后验均值和方差[18]。为进一步利用代理模型提供的信息,建立在高斯过程的基础上,贝叶斯优化的迭代过程可以定量地结合后验均值和方差,以平衡探索和利用[19]。文献[20-22]中,贝叶斯优化被用于模拟电路的优化,相对于进化算法,贝叶斯优化表现出了明显的优势。文献[23]提出了使用贝叶斯优化进行湍流模拟的优化。文献[24-25]中,贝叶斯优化被用于机器学习的模型和超参数的优化。文献[7]中,贝叶斯优化被用于简单的单目标天线优化。2020年,在机器学习会议NeurIPS举办的黑盒函数优化竞赛中,大量的研究工作都是基于贝叶斯优化[26-30]。因此,本文在贝叶斯优化的框架下,研究天线的快速优化问题。

综合上述工作,本文首先建立直接从天线参数到综合目标函数的映射关系,以实现简洁的端到端优化方式。其中,目标函数综合了分目标和限制条件。基于建立的综合目标函数,使用高效的贝叶斯优化进行迭代。最后将提出的优化算法用于圆极化贴片天线[6]和平面八木天线[9]的优化。结果表明,本文算法的优化结果和优化速度都具有明显的优越性。

1 目标函数建立

多目标优化问题可以表示为以下形式:

maximize (f1(x),f2(x),…,fm(x))
s.t.ci(x)>0, ∀i∈1,2,…,Nc

(1)

式中:Nc为限制条件的个数;m表示目标函数的个数。在多目标优化中,首先需要找到帕累托前沿,然后通过合适的度量找到最终的解。通常,天线的优化问题可以抽象为上述形式。如果将多个分目标和限制条件综合为一个目标函数,优化综合的目标函数相当于考虑了限制条件情况下优化各个分目标[17],因此可以将总目标函数定义为

F=ggn(Fgn)+gS11(FS11)+gwp(Fwp)+gAR(FAR)+…

(2)

式中:Fgn表示增益目标函数；FS11表示S11目标函数；Fwp表示天线位置关系目标函数；FAR表示轴比目标函数；g**表示对应的分目标函数再取复合函数。对各个分目标函数、限制条件取不同的复合函数,使其对不同的取值区间有不同的敏感度,从而通过对目标函数值的优化引导天线优化的方向。

2 优化算法

2.1 高斯过程

2.1.1 模型简述

假设对于有限采样{x1,x2,…,xn}∈xd,向量[f(x1),f(x2),…,f(xn)]T满足多变量的高斯分布

(3)

式中:μ是一个n×1向量;K是一个n×n协方差矩阵。高斯过程可以完全被均值函数m(x)和协方差函数k(x1,x2)表示。式(3)中,均值向量μ由m(x)决定,μi=m(xi),∀i∈1,2,…,n,协方差矩阵由协方差函数表示为Kij=k(xi,xj)。

均值函数和协方差函数可以被看作是对未知单输出函数y=f(x)的先验估计。高斯过程的协方差函数也被称为高斯过程核函数。本文使用的核函数为Matérn,其形式为

(4)

核函数式(4)中的超参数可以通过对样本数据集的学习得到。

2.1.2 输出预测

假设训练集为D={X,y},对于仿真软件而言,其仿真结果为确定值,不需考虑观测噪声。其中X={x1,x2,…,xN},y={f(x1),f(x2),…,f(xN)}。给定一个新的输入点x*,则y*=f(x*)和y可表示为联合高斯分布:

(5)

式中:m=[m(x1),m(x2),…,m(xN)]T是一个N×1的均值向量,且有:

k(x*,X)=[k(x*,x1),k(x*,x2),…,k(x*,xN)]

(6)

k(X,x*)=k(x*,X)T

(7)

(8)

y*以y为条件的分布服从正态分布,其分布可以表示为

(9)

(10)

式(10)给出了输入点x*对应的输出预测均值和方差。

2.1.3 超参数学习

高斯过程的均值函数、协方差函数含有超参数,在采样数据集的基础上使用最大似然估计法学习超参数,提升对未知输入预测的准确度。似然的表达式为

(11)

将其转化为负对数边缘似然:

(12)

对其求解最小化,得到高斯过程的超参数θ。

2.2 贝叶斯优化

贝叶斯优化[19]由代理模型和获得函数两大部分构成。在高斯过程建立代理模型后,获得函数被用来进行迭代。

2.2.1 获得函数

本文使用的获得函数为置信上界(upper confidence bound, UCB)。假设已采样t-1次,得到数据集Dt-1={(x1,y1),(x2,y2),…,(xt-1,yt-1)}。则有

αUCB(x;θ,Dt-1)=μ(x;θ,Dt-1)+κσ(x;θ,Dt-1)

(13)

式中:κ控制迭代过程中探索与利用之间的平衡,κ越小,越偏向于利用;κ越大,越偏向于探索;θ为高斯过程的超参数。通过最大化获得函数,找到下一个需要探索的点。

2.2.2 优化过程

贝叶斯优化流程如图1所示,在优化过程中,首先随机采样一部分样本作为初始样本集;在每次迭代过程中根据样本集对模型进行训练;求解获得函数最大化找到下一个需要迭代的点;代入仿真软件进行电磁仿真;将仿真结果加入样本集;如果满足终止条件则结束。

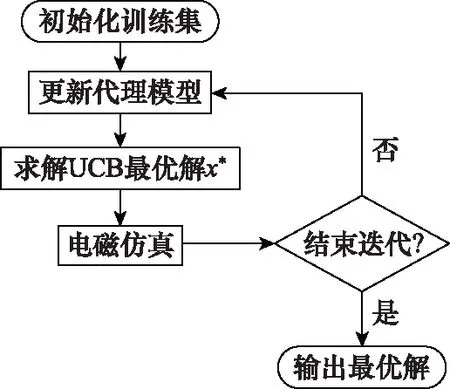
图1 贝叶斯优化流程图Fig.1 Flowchart of Bayesian optimization

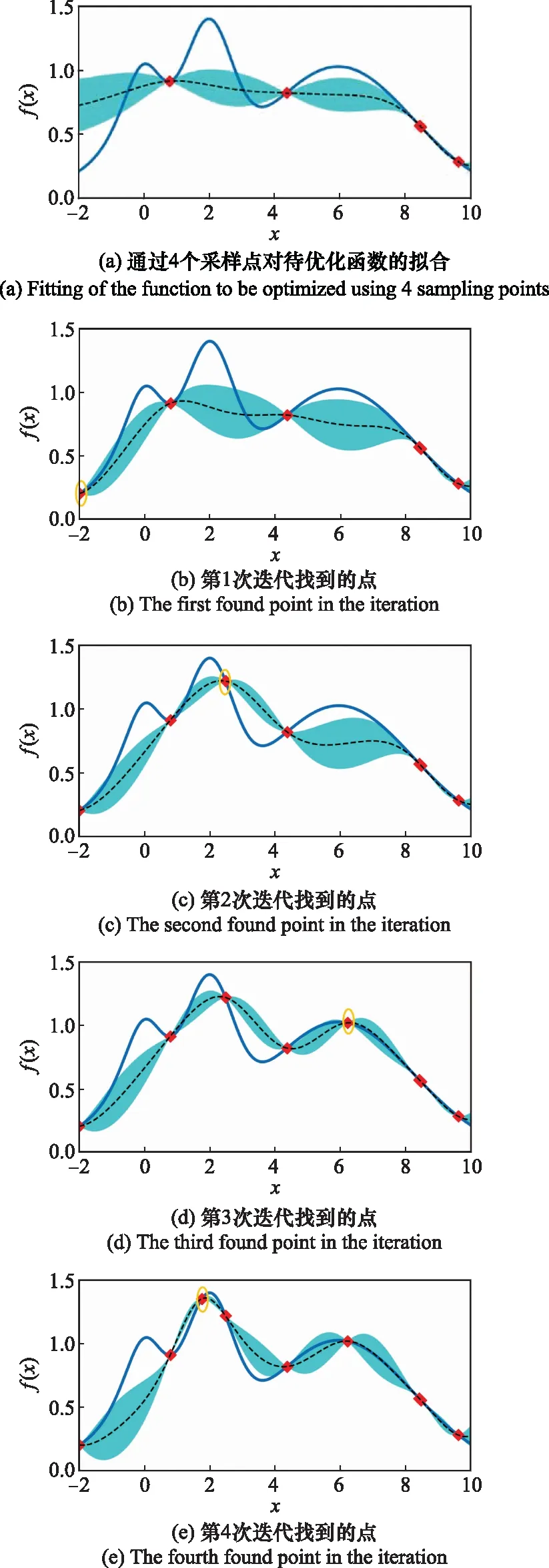
在图2所示的算例中,初始随机采样4个函数值,通过高斯过程根据样本集对待优化函数做出拟合,图2阴影部分表示估计的均值与±σ的范围,在代理模型的基础上使用获得函数找出下一个需要探索的点。在第6次迭代中,找到了几乎是待优化函数的最优解。

3 优化算法在天线中的验证

本节分别采用一个圆极化贴片天线[6]和一个平面八木天线[9]验证前文所述的优化算法,针对相同的问题对比本文提出的优化算法与引用文献中的优化算法,算法的比较主要体现在简洁程度、优化结果和优化速度3个方面。本文使用计算机配置为AMD 12-Core-3.8 GHz处理器, 64 GB内存,Windows 10操作系统;使用的仿真软件为Ansys-Ansoft HFSS 2019;编程语言为Python3.7;优化算法代码基于文献[31]。

3.1 圆极化贴片天线的优化

如图3所示,此天线[6]通过同轴馈电。介质的相对介电常数为εr=1.56,损耗角正切为tanδ=0.012,厚度为h=3.94 mm。分别在1.563 42 GHz、1.575 42 GHz和1.587 42 GHz频率下进行仿真求解。

图3 圆极化贴片天线模型Fig.3 Model of circular polarization patch antenna

在文献[6]中,优化目标为

(14)

式中:Gainmin为3个频点中增益最小值;ARmax为仿真最大轴比;ARlim为要求轴比上限(-3 dB);S11max为仿真最大S11;S11lim为要求S11上限(-10 dB)。优化参数(单位为mm)及优化区间为

(15)

在文献[6]中,作者用Kriging、径向基函数(radial basis function, RBF)、支持向量回归做代理模型集,迭代过程中对采样点的选取使用了基于提升概率(hypervolume-based probability of improvement, PoI)和可行性概率(probability of feasibility, PoF)的方法,迭代后得到帕累托前沿,其包含范围为2.81 dB≤AR≤3 dB、4.75 dB≤Gain≤4.85 dB、-30 dB≤S11≤-10 dB。再用超体积度量演进(evolution of the hypervolume metric, EoHE)找到其中一个最优解(AR=2.83 dB、Gain=4.82 dB、S11=-15.9 dB)。文中用了132个初始点,250次迭代。

在本文中,将目标函数转化为

f(xpatch)=10(3-ARmax)+0.2(-10-S11max)+
(Gainmin-4)

(16)

式中:xpatch表示为待优化的参数组合。为提高对ARmax的敏感性,将其对应的系数设置的为10;其次将Gainmin部分的对应系数设置为1;相对而言,S11max最容易被优化到-10 dB以下,将其对应的系数设置为0.2。为验证高斯过程的拟合效果,随机生成55个样本点,随机选择其中50个样本点作为训练集,剩余5个样本作为测试集,其拟合值和真实值的对比如表1所示。在贝叶斯优化中,将初始化采样数量设为50,将迭代步数设为200。将优化算方法重复3次得到图4,优化结果总结如表2所示。

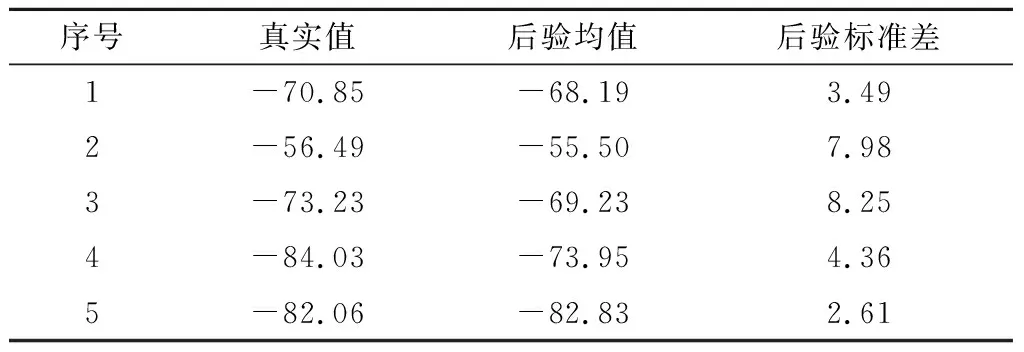
表1 高斯过程在圆极化贴片天线上的拟合

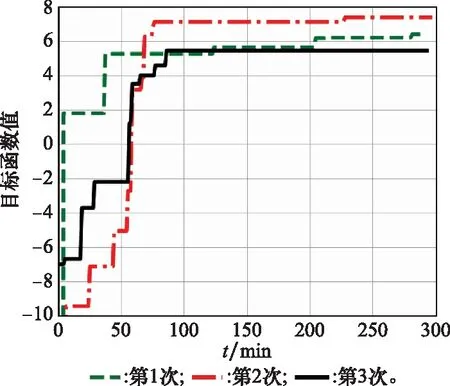
图4 圆极化贴片天线目标函数取值随时间变化Fig.4 Objective function value changing with time consumption in the circular polarization patch antenna

表2 圆极化贴片天线优化结果

从表1可以看出,高斯过程有效地预测了待优化的目标函数。从表2可以看出,3次优化均得到了优于文献[6]的结果;虽然初始随机样本点为50,迭代次数为200,但是可以看出,大约只用到三分之一的样本数就达到了优于文献[6]的优化结果;优化算法本身耗时36 s;而且,整个优化过程以端到端的方式实现。

3.2 平面八木天线的优化

如图5所示,平面八木天线由微带巴伦、共面馈电带线、有源振子和引向器组成。介质为厚度0.635 mm的Rogers RT6010,金属化为35 μm的铜。待优化的参数为x=[s1,s2,v1,v2,u1,u2,u3,u4]T,其他参数满足w1=w3=w4=0.6,w2=1.2,u5=1.5,s3=3.0,v3=17.5(单位为mm)。在文献[9]中,优化目标为

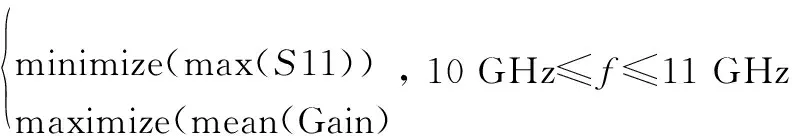
(17)

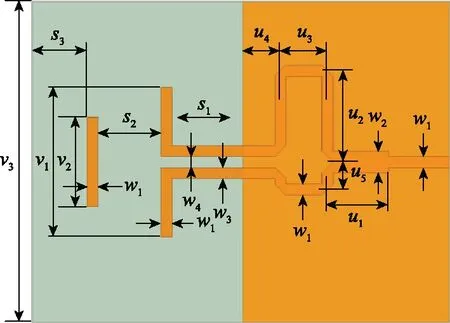
图5 平面八木天线模型Fig.5 Model of planar Yagi antenna

优化参数(单位为mm)的范围为

(18)

文献[9]使用了Kriging和Moea的算法。在频段内取多个频点,针对每个频点建立代理模型;由于天线的设计参数空间维度较高,在部分代理模型的建立过程中,整个结构被分为天线部分和巴伦馈电部分进行仿真和建模。经过约47 h的优化得到帕累托前沿如图6所示。

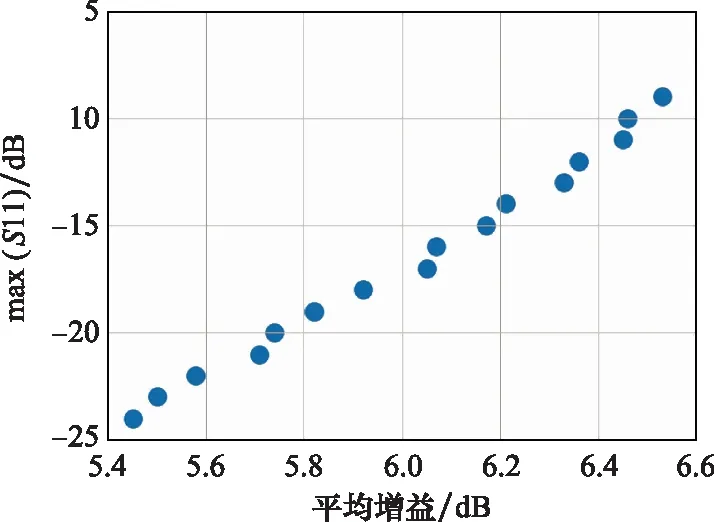
图6 平面八木天线对比文献[9]中的优化结果Fig.6 Optimized results of planar Yagi antenna in [9]

在本文中,将其转化为综合的单目标优化的问题:

f(xYagi)=fs(-10-max(S11(f))+
7(mean(Gain(f))-4)

(19)

(20)

在这里,将fs设置为分段线性函数,使其对不同的max(S11(f))取值范围有不同的敏感度,当max(S11(f))低于-15 dB后,继续降低max(S11(f))带来的收益非常小,此时应将更多的优化重心放到天线增益上。

在本文中,将整个天线作为一个整体进行仿真和优化。为验证高斯过程的拟合效果,随机生成105个样本点,随机选择其中100个样本点作为训练集,剩余5个样本作为测试集,其拟合值和真实值的对比如表3所示。在贝叶斯优化中,将初始化样本集设为100,优化迭代步数设为200。将优化算法重复运行3次,优化过程如图7所示。每一次的优化结果总结如表4所示。

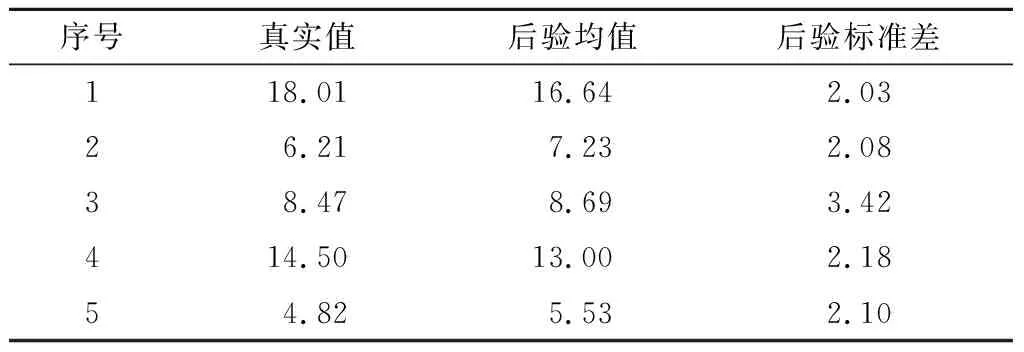
表3 高斯过程在平面八木天线上的拟合

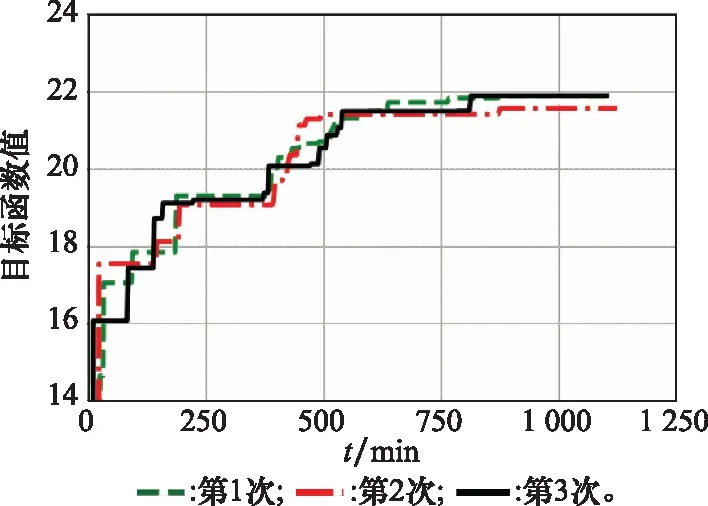
图7 平面八木天线目标函数取值随时间变化Fig.7 Objective function value changing with time consumption in planar Yagi antenna optimization

表4 平面八木天线优化结果

从表3可以看出,高斯过程有效地预测了待优化的目标函数。从表4可以看出,本文优化算法得到的效果优于文献[9],尽管在图6中,最优平均增益达到了约6.52 dB,但是其S11值明显不符合要求。在本文中,天线整个优化耗时约为16.7 h,优化算法本身耗时79 s;原文献对频段范围内多个频点分别建立代理模型,由于优化参数空间(8维)过大,原文献在部分代理模型建立中采取了馈电部分和辐射部分分开仿真的做法,而在本文中,整个优化过程以端到端的方式实现。

4 结 论

本文首先使用端到端的方法建立天线优化的综合目标函数,精简后续优化过程。在综合目标函数建立的基础上,提出使用贝叶斯优化算法对天线进行优化。将优化算法用在圆极化贴片天线和平面八木天线上进行了验证。相较于对比文献,本文提出的优化算法有更好优化结果、更快的优化速度,且优化过程简洁,以端到端的方式实现。尽管本文使用综合目标函数方法定义出的目标函数并非理论上最优,但是通过3个天线算例的仿真和对比,表明与现有方法相比,其优化结果具有明显的优越性。