初始裂纹对超高压容器疲劳寿命的影响研究*

高耀东,王壮壮,郭忠亮

(内蒙古科技大学 机械工程学院,内蒙古 包头 014010)

0 引 言

随着现代工业的高速发展,高压容器在各行各业已得到了广泛应用。

作为一种需要承受一定压强,进行贮存、运输或反应的密闭容器,其工作介质往往具有易燃、易爆、有毒或腐蚀性的特性;同时,其工作条件苛刻,经常伴随着高温、高压、高真空等环境,所以其使用的安全性一直是所有企业工作的重点[1,2]。据统计,20世纪60年代以来我国的压力容器破坏事故中,有62%是由疲劳裂纹引起的[3],所以压力容器的设计、制造和维护检测有着极高的要求[4],其能否安全运行不仅关系着工业生产的经济效益,更关系着人民的生命财产安全。

近几年,许多学者对压力容器表面裂纹进行了不断的分析研究。靖维飞等人[5]针对超高压容器表面的裂纹缺陷,采用有限元仿真方法对其进行了寿命分析,其研究结果认为,内表面裂纹在尺寸较小时就会对容器的疲劳寿命产生较大的影响。毛志辉[6]、涂思浩[7]等人对不同压力容器的内部表面裂纹缺陷疲劳寿命进行了分析,从分析结果可以看出,初始裂纹尺寸对整体疲劳寿命的影响较大。常磊等人[8]对不同服役周期下表面裂纹的临界尺寸进行了研究,从其结果可以看出,深度尺寸的变化要明显大于长度。张洋洋等人[9]对压力容器上的表面裂纹进行了不同长短轴比的初始裂纹扩展仿真研究,其研究结果表明,在裂纹扩展中深度方向的速率要大于长度方向。

以上研究大多针对的是不同条件下的表面裂纹扩展特性,且均采用的是有限元仿真模拟的单一方法。

本文基于美国机械工程师学会(ASME)编制的ASME Ⅷ-3《高压容器建造另一规则》[10],针对表面裂纹缺陷的疲劳扩展寿命提出一套分析和计算方法;对算例进行裂纹疲劳寿命计算,并通过建立多组初始裂纹尺寸模型进行计算;对比分析初始裂纹尺寸对于疲劳裂纹扩展寿命的影响。

1 ASME中断裂力学计算方法

ASME规范在其KD-4章以及非强制附录D中给出了关于高压容器断裂力学的分析及计算方法。本文以包头科发高压公司的超高压容器为例,对其进行假设初始裂纹的疲劳寿命计算。

含表面裂纹缺陷的超高压容器筒体如图1所示。

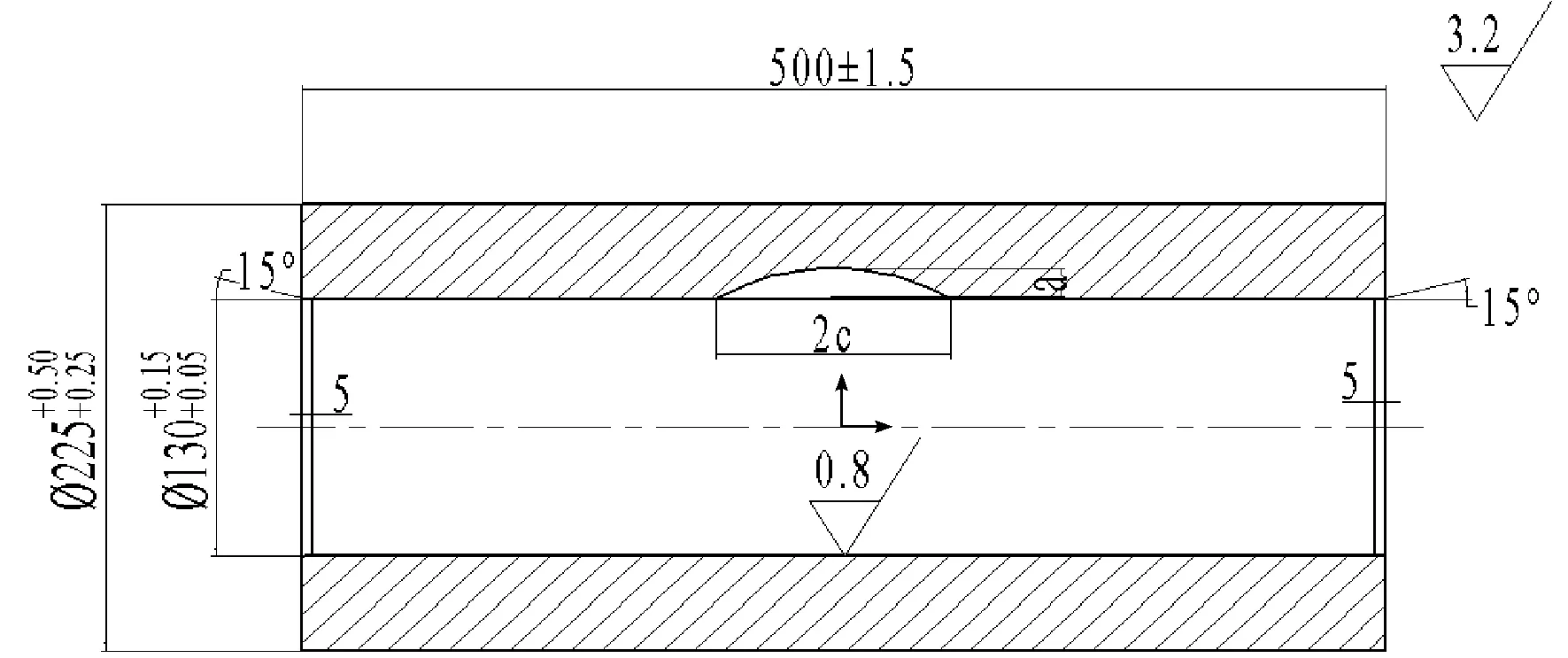
图1 含表面裂纹缺陷的超高压容器筒体

图1中:筒体长500 mm;内径65 mm;壁厚47.5 mm;内壁表面椭圆状裂纹的初始裂纹长度2c为4.275 mm;深度为1.425 mm;容器制造、加工标准为ASME规范要求标准;

容器采用材料编号SA-750M Type630.Condition-H1075,为马氏体沉淀硬化不锈钢;抗拉强度Su=1 000 MPa;屈服强度Sy=860 MPa;夏比V型缺口冲击功CVN=30 J;

设计压力为150 MPa,使用压力为140 MPa;工作状态时受脉动循环应力,一次加压泄压为一个循环次数。

在计算疲劳裂纹扩展寿命时,需要给定初始裂纹尺寸以及临界裂纹尺寸。对于初始裂纹的尺寸,ASME要求基于无损检测方法得出,即如果裂纹尺寸可被无损检测方法精确探测,则可以使用。

对于裂纹扩展的临界尺寸,ASME规定需要使用API579/ASME FFS-1规范[11]中的失效评估图(FAD)判断得出,如图2所示。

图2 FAD失效评估图

在设计、制造、检验和测试等方面,API标准为压力容器、管道系统、储油罐等承压设备给出了较详尽的指导规范[12]。其中,FAD图可以用来检查在役设备的结构完整性,并用来确定含有缺陷的承压设备能否继续安全工作一段时间[13]。

图2中,以计算裂纹在扩展中的韧性比与载荷比来获得一组坐标,而图中的曲线为失效评估线,坐标点在评估线左侧为安全,在右侧为危险。所以笔者通过坐标点来判断当前尺寸裂纹是否安全,以确定裂纹在扩展中的临界尺寸。

接下来,笔者对以上提到的疲劳裂纹扩展寿命进行计算,并对裂纹扩展临界尺寸计算的方法进行介绍。

ASME在非强制性附录D中给出了疲劳裂纹扩展寿命的计算方法。首先,对于应力强度因子,采用多项式拟合的方法,对于裂纹深度方向有:

σ=A0+A1(x/a)+A2(x/a)2+A3(x/a)3

(1)

式中:A0,A1,A2,A3—常数系数,系数A0到A3应能准确表示分析所涵盖的缺陷深度上0≤x/a≤1的应力;a—裂纹深度。

本文以算例中纵向表面裂纹为例,由Lame公式计算得出裂纹所承受的周向应力为σ:

(2)

式中:Pi—圆筒内筒所受内压;P0—圆筒所受外压;ri—圆筒内筒的内半径;r—圆筒任意点半径;K—筒体的径比。

表面缺陷的应力强度因子使用三次多项式应力关系来计算,即:

(3)

式中:G0,G1,G2,G3—自由表面修正系数,需要查表得出,分为裂纹表面和裂纹最深处,分别计算裂纹长度和深度的扩展;Q—缺陷形状参数,Q=1+4.593(a/l)1.65-qy;l—缺陷长度;qy—塑性区修正系数,当进行疲劳裂纹扩展计算时可以设为0。

在扩展中,需要对每个新的裂纹尺寸的应力强度因子进行计算,以确定一组新的A0到A3,其中：AP为容器内部压力。

在得出应力强度因子后,再进行裂纹扩展速率的计算。该计算的设计循环数是将假定初始缺陷尺寸的裂纹扩展到允许的最终裂纹深度的循环次数,即da/dN(单位：m/cycle),具体如下:

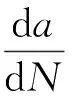
(4)

(5)

(6)

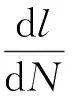
(7)

ΔKth=G(1-HRK)

(8)

式中:KIres—裂纹残余应力强度;RK—应力强度因子比;f(RK)—通过应力强度因子比值经查表可得。

ASME中规定的门槛ΔK(ΔKth)可由式(8)得出。如果ΔK值小于ΔKth,则值da/dN为0,即表示裂纹不发生扩展。

通过以上公式可以对给定裂纹进行扩展计算,每次给定扩展量,直至裂纹扩展到其临界深度尺寸,即计算得出疲劳裂纹的扩展寿命。

接下来,笔者使用API579中关于临界裂纹尺寸的判断方法,来计算得出算例中裂纹的临界尺寸。其中,计算载荷比(FAD图横坐标)为:

(9)

主应力的计算式为:

(10)

式中:g，α—参考应力系数;Pm—主膜应力分量;Pb—主弯曲应力分量;Ms—表面裂纹的表面修正系数;Mt—穿透裂纹修正系数;λa—确定表面修正系数的壳参数;σys—材料屈服强度;a—裂纹深度;c—裂纹长度;t—容器壁厚;p—容器内部压力;Ri—容器内径。

韧性比(FAD图纵坐标)计算式为:

(11)

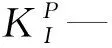
经计算得出的裂纹扩展失效路径如图3所示。

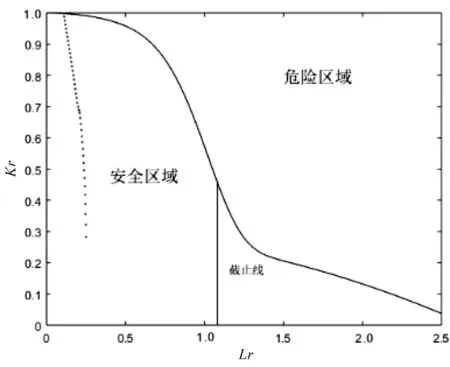
图3 裂纹失效路径图

经计算,得出此容器表面裂纹的临界裂纹深度尺寸为a=21.625 mm。

在获得裂纹的临界深度尺寸后,即可对裂纹的疲劳扩展寿命进行计算。经对算例中给出的裂纹进疲劳裂纹扩展寿命进行计算,得出裂纹扩展寿命N=33 214。该结果证明该计算方法是可行的。

2 初始裂纹对应力强度因子的影响

应用ASME中断裂力学分析的计算方法,笔者接下来分析不同初始裂纹的尺寸对应力强度因子,以及疲劳裂纹扩展寿命的影响。

首先,对初始裂纹的应力强度因子进行计算分析,分别建立5组不同初始裂纹尺寸模型,其深度分别为0.5 mm、1 mm、1.5 mm、2 mm、2.5 mm,长度尺寸分别为5 mm、6 mm、7 mm、8 mm、9 mm;对容器内壁含轴向表面裂纹进行多组数据计算,通过改变其初始裂纹深度和长度,得出裂纹应力的强度因子数据。

经过计算可得出裂纹最深点与表面点的应力强度因子,其计算结果如表1所示。

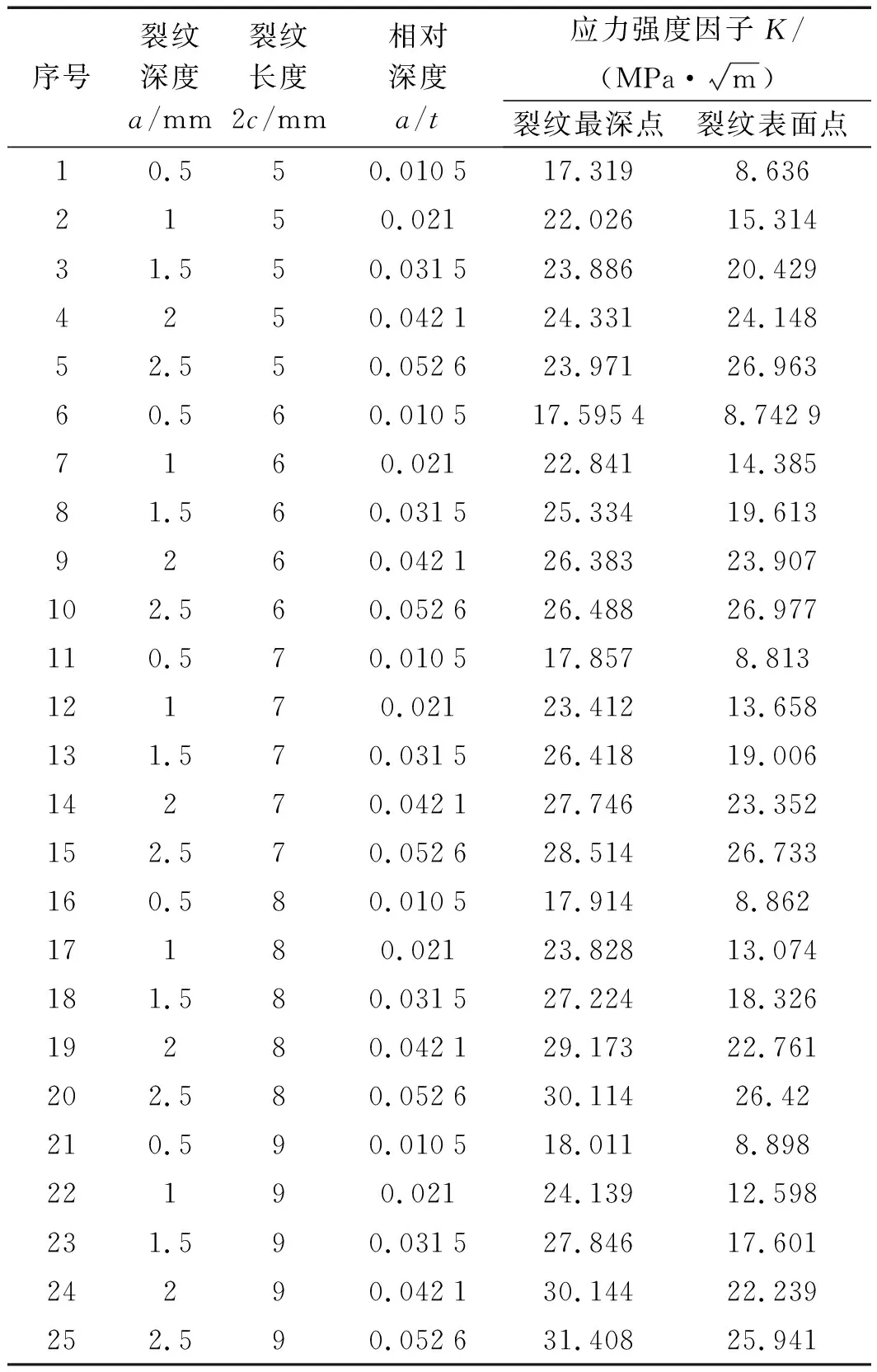
表1 不同初始裂纹尺寸对裂纹最深点应力强度因子计算

2.1 裂纹最深点应力强度因子

笔者根据计算所得结果的数据,绘制成图。其中,裂纹最深点应力强度因子随初始裂纹的深度改变的变化图,如图4所示。

图4 应力强度因子随裂纹深度变化图

由图4可以看出:当裂纹长度一定时,裂纹最深点的应力强度因子随着裂纹深度的增加而持续增加,二者成正比;且在深度尺寸较小时,其差值较大。

裂纹最深点应力强度因子随初始裂纹的长度改变的变化图,如图5所示。

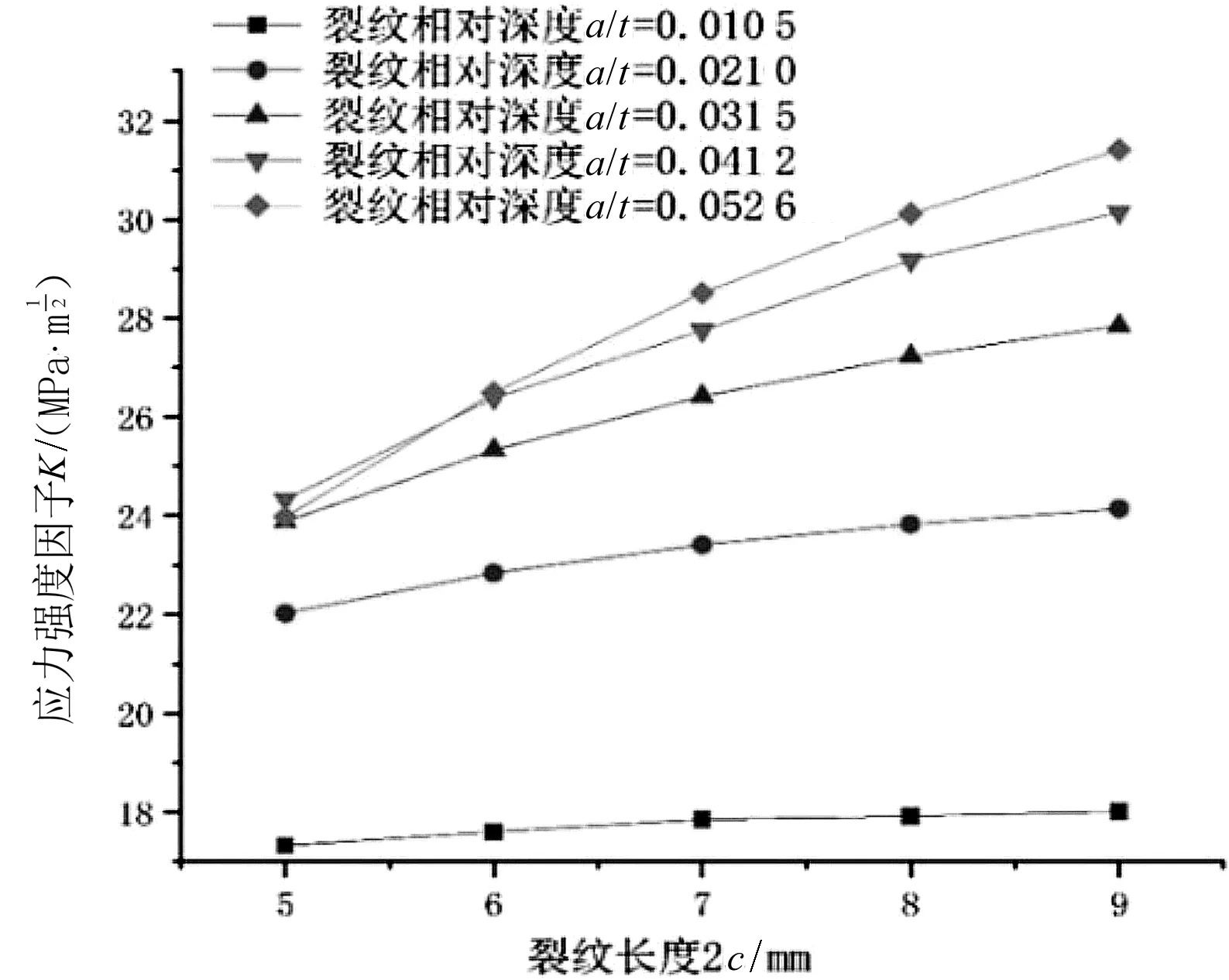
图5 应力强度因子随裂纹长度变化图

由图5可以看出:在裂纹的相对深度一定时,随着裂纹长度的增加也会使裂纹的最深点应力强度因子值增加;但相对于裂纹深度尺寸变化的影响,在相对深度一定时,长度尺寸对于裂纹最深点应力强度因子影响较小,且深度尺寸越大其增长越平缓。

从图(4,5)还可以看出:随着裂纹深度尺寸增加,裂纹最深点应力强度因子会明显加大;同时,与其相比,裂纹长度尺寸改变引起的应力强度因子变化对其影响相对较小,而且在裂纹相对深度较小时的影响几乎可以忽略不计。

2.2 裂纹表面点应力强度因子

裂纹表面点应力强度因子随初始裂纹的深度改变的变化图,如图6所示。

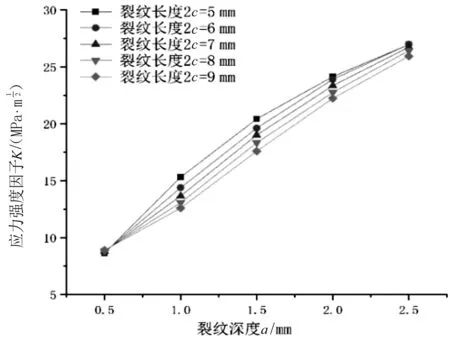
图6 应力强度因子随裂纹深度变化图

由图6可以看出:随着初始裂纹深度尺寸的增加,其裂纹表面点的应力强度因子增大,二者成正比,且增值较大。

裂纹表面点应力强度因子随初始裂纹的长度改变的变化图,如图7所示。

由图7可以看出:裂纹表面点应力强度因子随长度尺寸的增加而减小,二者成反比;而当长度一定时,裂纹深度尺寸对裂纹表面点的应力强度因子影响明显大于长度尺寸。

所以,对比图(6,7)可以看出:对于裂纹表面应力强度因子,裂纹深度尺寸的影响也要大于裂纹长度尺寸的影响。

通过对应力强度因子的计算可以看出,对于初始裂纹的最深点与表面点的应力强度因子,其深度尺寸的影响要大于长度尺寸的影响,同时也会对裂纹的扩展产生相应的影响。

3 初始裂纹对疲劳裂纹扩展寿命的影响

使用同样的初始裂纹尺寸模型,笔者对容器内壁含轴向表面裂纹进行多组数据计算,即计算其在不同初始裂纹尺寸时,裂纹扩展的循环次数(即裂纹扩展寿命);此处分别以扩展一次0.5 mm与整体疲劳裂纹扩展至21.625 mm的情况为例。

经过计算得出的数据如表2所示。

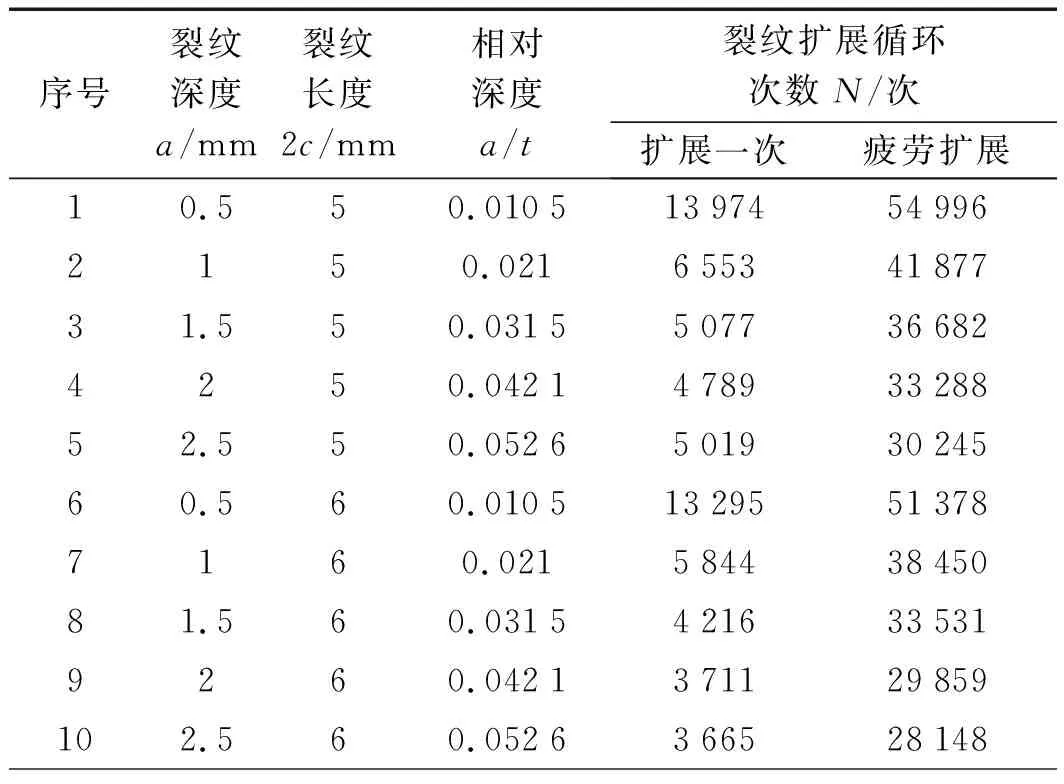
表2 不同初始裂纹尺寸对裂纹表扩展的影响

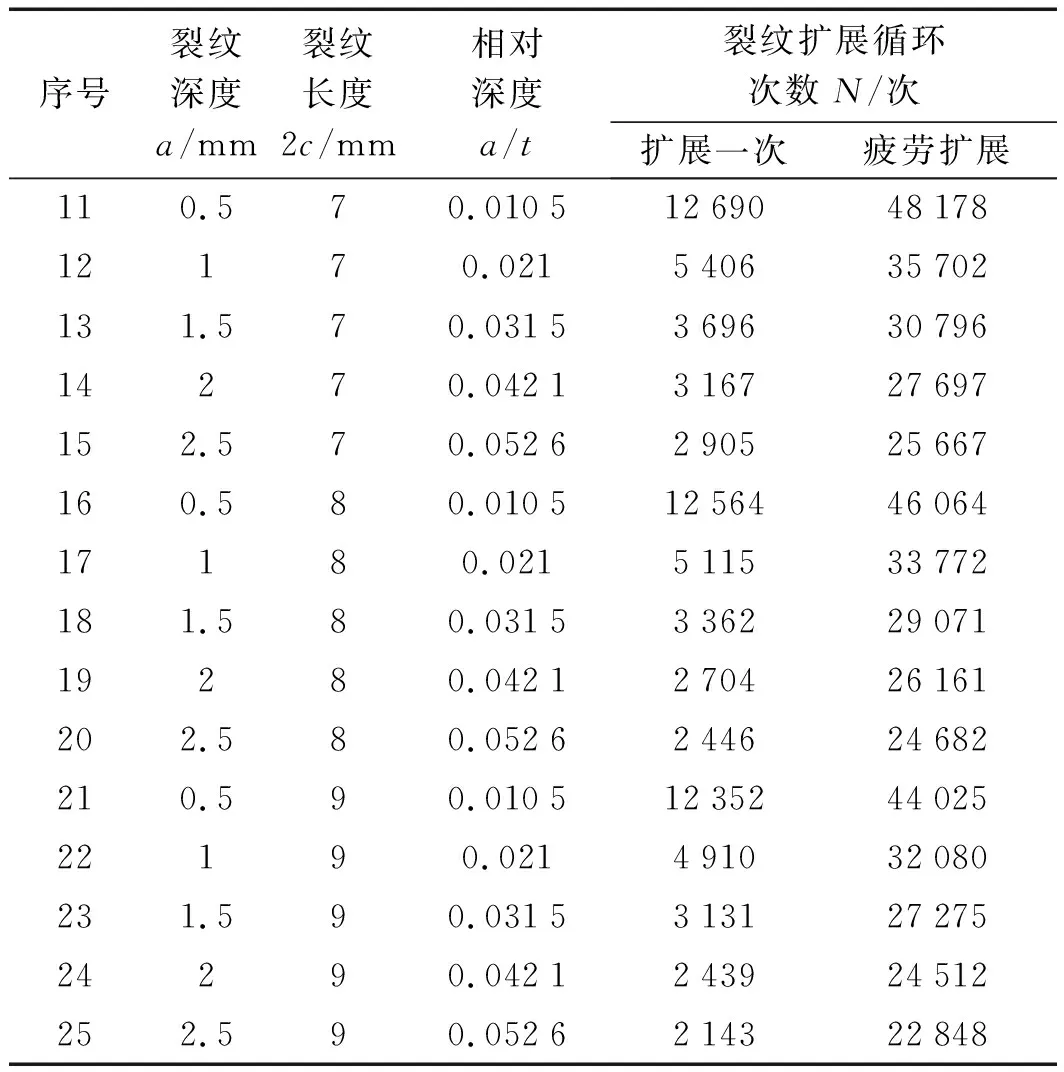
(续表)

3.1 裂纹扩展一次情况

根据表2中的计算结果,笔者将其分别绘制成图。其中,裂纹仅扩展一次的情况下,扩展循环次数随初始裂纹的深度改变的变化图,如图8所示。

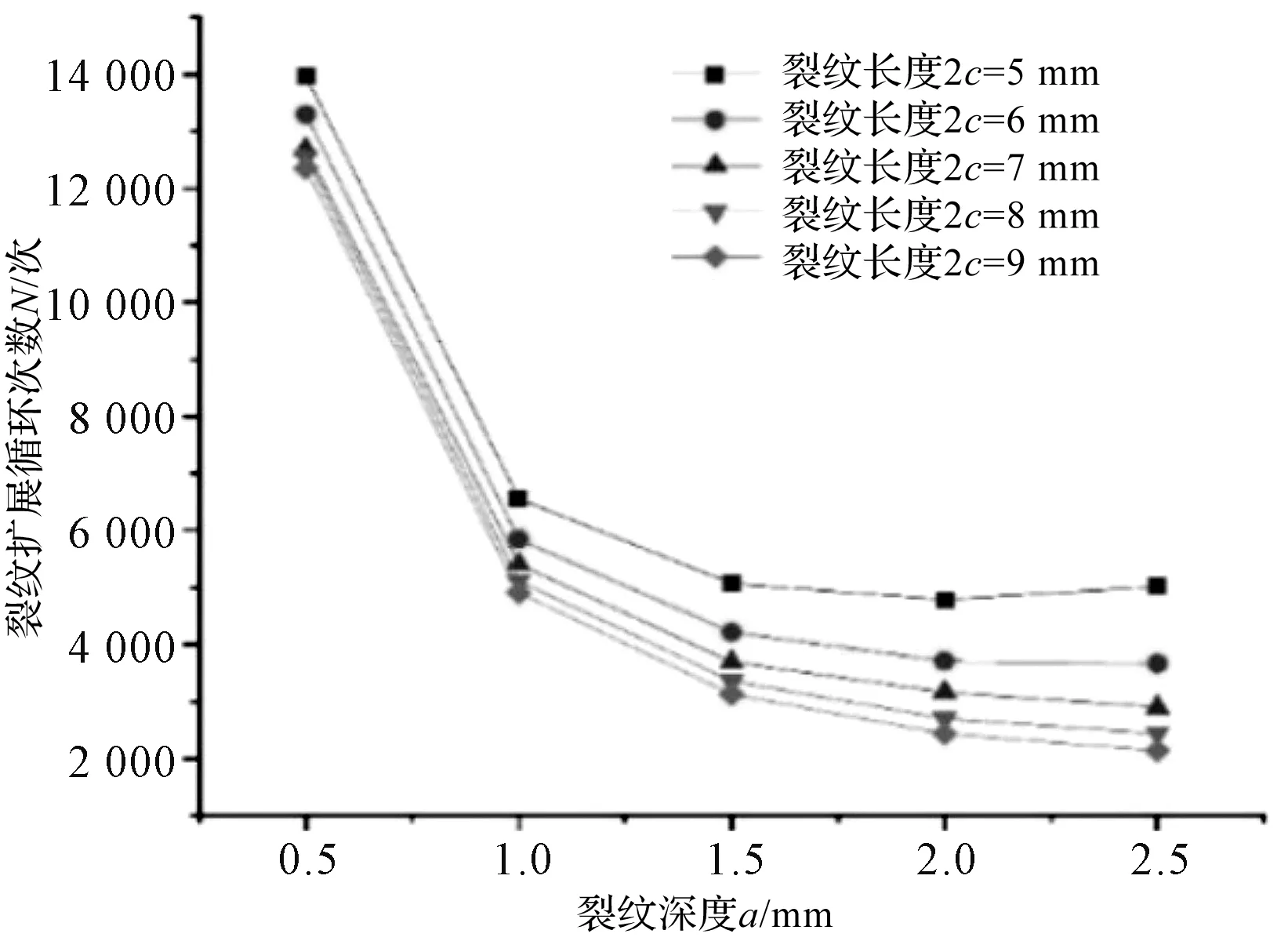
图8 裂纹扩展循环次数随裂纹深度变化图

由图8可以看出:对于裂纹仅扩展一次的循环次数,在裂纹长度一定时,裂纹深度与裂纹扩展循环次数成反比,即当裂纹深度增加时,裂纹扩展循环次数减少;同时,观察图中5组不同长度尺寸裂纹数据可以看出,裂纹扩展循环次数降低的趋势大致相同,即在0.5 mm～1.5 mm时降低趋势较较大,而在1.5 mm～2.5 mm降低趋势较缓和。由此可见,在尺寸较小时,裂纹深度对裂纹扩展循环次数的影响非常大。

裂纹仅扩展一次的情况下,扩展循环次数随初始裂纹的长度改变的变化图,如图9所示。

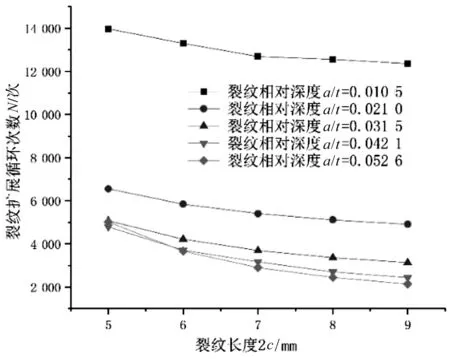
图9 裂纹扩展循环次数随裂纹长度变化图

由图9可以看出:在裂纹相对深度一定时,裂纹长度尺寸与裂纹扩展循环次数同样成反比,即当裂纹长度增加时,裂纹扩展循环次数减少;观察图9中5组不同裂纹相对深度数据可以看出,相比图8,其变化趋势相对平缓,整体变化趋势不太明显。

由此可以看出,初始裂纹深度对初始裂纹扩展一次的循环次数影响较大,这对其疲劳扩展也会产生相应的影响。

3.2 整体疲劳裂纹扩展情况

在整体疲劳裂纹扩展情况下,扩展寿命随初始裂纹的深度改变的变化图,如图10所示。

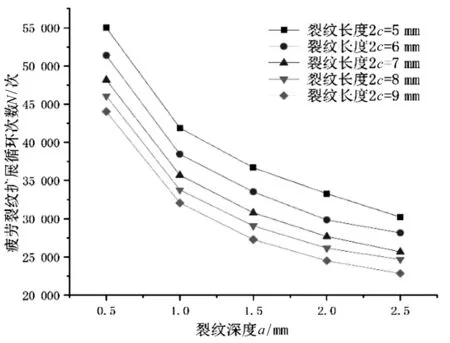
图10 疲劳裂纹扩展循环次数随裂纹深度变化图

由图10可以看出:疲劳裂纹扩展循环次数与裂纹深度成反比,且其变化趋势相同;对比图8可见,其整体下降趋势稍缓和,但同样在0.5 mm～1.5 mm阶段的变化趋势大于1.5 mm～2.5 mm,与图8一致。该结果也说明,初始裂纹尺寸对于整体疲劳裂纹扩展影响较大。

在整体疲劳裂纹扩展情况下,扩展寿命随初始裂纹的长度改变的变化图,如图11所示。

图11 疲劳裂纹扩展循环次数随裂纹长度变化图

由图11可以看出:疲劳裂纹扩展循环次数与裂纹长度成反比,该趋势与图9的整体趋势相同,且其趋势相比图10较为缓和;相比初始裂纹深度尺寸的影响,长度尺寸的影响要小于深度尺寸,对于疲劳裂纹扩展,初始裂纹尺寸的深度影响可能会转变为长度的影响。由此可见,初始裂纹深度尺寸在裂纹扩展中至关重要。

结合图(8～11)可以看出:初始裂纹尺寸对于疲劳裂纹扩展循环次数的影响比较大,首次扩展的循环次数占整体疲劳扩展循环次数在9.379%至28.057%之间;尤其是初始裂纹深度尺寸会对疲劳裂纹扩展循环次数,即疲劳裂纹扩展寿命产生更大的影响。

4 结束语

本文采用ASEM中断裂力学的分析计算方法,对算例中的表面裂纹进行了疲劳裂纹扩展寿命计算,并经过对比计算,分析了不同尺寸初始裂纹对疲劳裂纹扩展寿命的影响。

研究结果表明:

(1)初始裂纹尺寸对于裂纹的应力强度因子,以及疲劳裂纹扩展寿命都有着巨大的影响;

(2)初始裂纹深度尺寸对于裂纹的最深点与表面点的应力强度因子影响要远大于其长度尺寸,且会影响其在裂纹扩展中的循环次数;

(3)对于疲劳裂纹寿命,数据表明初始裂纹扩展一次的循环次数在总体疲劳裂纹扩展循环次数中占比较大,所以初始裂纹尺寸对疲劳裂纹扩展寿命的影响较大,且初始裂纹深度尺寸的影响要大于长度尺寸的影响。

在后续的研究工作中,笔者将对初始裂纹深度方向更准确的数据获取方式进行研究,以保证设备能在一个合理的工作寿命内工作。