裂纹故障下轴承浪型保持架的动态特性分析*

谢宏浩,牛蔺楷,2*,肖 飞,祁宏伟,郑一珍,熊晓燕,2

(1.太原理工大学 机械与运载工程学院,山西 太原 030000;2.太原理工大学 新型传感器与智能控制教育部重点实验室,山西 太原 030000)

0 引 言

轴承保持架是指部分地包裹全部或部分滚动体,并随之运动的轴承零件,其作用是隔离滚动体,引导滚动体并将其保持在轴承内。

作为滚动轴承的重要组成部分,轴承保持架的成本约占整个轴承的20%到30%,其稳定与否直接影响轴承的运转状态。保持架的轻微故障会引发其他部件也出现故障,且难以分析故障产生的原因,严重的保持架故障例如保持架卡死,会造成重大的事故。

裂纹是一种常见的保持架故障类型,且裂纹萌生初期往往难以发现,原因在于相比于球与故障套圈之间相互作用造成的冲击,球与故障保持架之间相互作用造成的冲击存在幅值较小,且周期性不强的特点,故无法直接在时域及频域图上得到清晰的保持架故障指标,更无法有效地判断轴承保持架是否发生了故障。

作为深沟球轴承,浪型保持架是其常用的一种保持架。不同于其他类型的保持架,该类型保持架不由套圈引导而是直接由球引导,因此,其球与故障保持架之间的互相作用更加频繁,更容易引发保持架出现疲劳裂纹的故障。

多年来,有众多专家学者对轴承保持架故障做了大量的分析研究。唐德尧[1]提出了一种联合轴承保持架故障特征谱与外孤谱的保持架变形识别方法。李修文等人[2]提出了一种基于整周期时域回归的方法,来提取出轴承滚子之间的间距变化信息,进而判断轴承保持架是否出现了故障。但上述两种方法对其有效使用的场合较为严苛。

郑一珍等人[3]提出了一种基于EMD分解振动加速度信号的SDP特征融合的,卷积神经网络轴承故障类型诊断法。韩清鹏等人[4]提出了一种基于ARMA模型使用时域指标参数,对滚动轴承故障进行诊断的方法。但这两种方法对不同使用场合下的轴承自适应性不强。

针对不同类型的轴承保持架,研究其正常状态与故障状态下不同的动态特性,揭示其故障的动力学机理,对于轴承保持架的故障诊断具有重要意义[5]。因此,对于该类型故障,直接从故障保持架自身的动态特性入手,得到故障特征,对于更好地对保持架裂纹故障进行诊断有一定的促进作用。

针对该类型轴承保持架,笔者采用将不同裂纹保持架离散为柔性体后,再进行动力学仿真分析的方法,来研究保持架的动态特性。

1 球轴承多体动力学模型

1.1 模型的建立

轴承内部保持架与球均具有6个自由度,且保持架引导方式为球引导,二者之间的互相作用频繁,并且不具有很强的规律性,使得整个轴承系统内部的动力学求解过程复杂。因此,本文运用多体动力学软件ADAMS建立球轴承的多体动力学模型[6],进而对保持架动态特性进行分析。

此处笔者分析所用的球轴承为深沟球轴承6205,其具体结构参数中,径向游隙与保持架兜孔间隙取文献[7]中振动加速度级最小时所对应的值。

对于轴承所设的约束为:

(1)外圈固定,0个自由度;

(2)内圈设置为平面副,保留绕轴线旋转和径向平面内的平动3个自由度;

(3)球与保持架均保持6个自由度[8-10];

(4)球与内圈、外圈、保持架之间设置为体对体接触。

1.2 保持架裂纹建模及柔性化处理

保持架裂纹的具体建模工作由三维建模软件来完成。此处设定裂纹宽度为1 mm,深度分别为0.35 mm、0.7 mm、1.05 mm、1.4 mm及1.75 mm(断裂)。后续提到裂纹将只表示深度,不再体现宽度。

裂纹的设定位置为铆钉与兜孔之间,笔者并在此处作如下假设:裂纹主要是由疲劳产生,因此不考虑因工艺装配误差、运转过程中,异物入侵、铆钉缺陷等等因素产生的其余形式的保持架裂纹。

此处将轴承保持架离散为柔性体,更能准确、真实地表达保持架的动态特性,也更接近于其真实的运行情况[11]。保持架柔性化采用模态综合法,在ADAMS/FLEX中实现。离散保持架时选择体单元,手动选择单元大小为确保精度前提下的最优化仿真速度的值;模态选择18阶模态,其中,前6阶模态为刚性模态,FLEX系统默认选择其为无效模式。

对于柔体保持架而言,此处在ADAMS中选择观察其模态初始条件,可以得到其各阶固有振动频率。

各深度裂纹的保持架部分阶数固有振动频率如表1所示。

从表1中可以看出:当保持架出现裂纹后,保持架的固有振动频率下降,这意味着相比于正常保持架,出现裂纹的保持架产生共振现象的可能性增加。

表1 不同裂纹保持架固有振动频率表

保持架出现裂纹后其整体刚度减小,会导致其固有振动频率减小。其原因在于,保持架断裂后其已经不再属于圆环类零件,整体刚度下降明显,故固有振动频率远远小于未完全断裂时;同时,与未断裂保持架相比,断裂的保持架也更易产生共振。

1.3 接触参数的计算

在接触分析中,软件自带惩罚函数法与Impact法。本文选择Impact法的原因在于:(1)惩罚函数法适用于动力学中的间歇性接触,用于持续性接触则有可能造成颤振或者轻微的约束失效;(2)Impact法具有更强的鲁棒性以及对求解器公差范围的低敏感性,且它也是唯一可以用于柔性体接触的方法[12]。

本文通过计算接触刚度和油膜刚度的方法,来求解考虑弹流润滑的保持架综合刚度[13]。

1.3.1 球与滚道、保持架接触刚度计算

套圈滚道的曲率半径系数为:

(1)

式中:r—滚道曲率半径;Dw—球的直径。

套圈主曲率的计算公式表如表2所示。

表2 套圈主曲率计算公式表

ρ1I,ρ1II—滚球表面接触点在轴向、径向平面内的主曲率;ρ2I,ρ2II—滚道表面接触点在轴向、径向平面内的主曲率

笔者在求得内外套圈滚道的曲率半径系数后,将其代入表2中,来分别计算内外套圈的主曲率。

设定1为滚球,2为滚道,I为轴向平面,II为径向平面。

平面主曲率之和的计算式为:

∑ρ=ρ1I+ρ1II+ρ2I+ρ2II

(2)

由以上参数可计算滚球与内外滚道之间的接触刚度系数,即:

Kj=2.15×105(∑ρ)-0.5(nδ)-1.5

(3)

而对于球和保持架兜孔之间接触刚度,其表达式为:

(4)

其中:

k=1.033 9(Rη/Rε)0.636 0

(5)

R=RεRη/(Rε+Rη)

(6)

Rε=0.5DwDp/(Dp-Dw)

(7)

Rη=0.5Dw

(8)

ε=1.000 3+0.596 8Rε/Rη

(9)

Γ=1.527 7+0.602 3ln(Rη/Rε)

(10)

式中:Dp—保持架兜孔直径。

1.3.2 球和滚道、保持架兜孔油膜刚度

接下来,笔者对球和滚道、保持架兜孔油膜的刚度进行具体计算。

对于内圈而言,有:

(11)

对于外圈而言,有:

(12)

其中:

(13)

(14)

(15)

(16)

式中:a—所用润滑油黏度的压力系数;η0—常压下的动力黏度;n—内圈或外圈的转速,r·min-1;rj—无量纲参数;dm—节圆直径;E0—等效弹性模量;u—泊松比;E—弹性模量;e—自然对数的底;Qmax—受载最大的滚动体负荷;Fr—径向载荷;Z—滚动体个数。

对于保持架兜孔[14，15]而言,有:

hmin=|Cp-Zc|

(17)

(18)

Rx=0.5Dw

(19)

式中:Cp—保持架兜孔的间隙;wc—保持架公转的角速度;wok—第k个钢球的公转速度。

油膜的刚度公式为:

(20)

(21)

(22)

Vm=0.5Dwwb

(23)

Rx=0.5Dw(1-r)

(24)

Rx=0.5Dw(1+r)

(25)

G=aE0

(26)

式中:U—无量纲速度参数;Vm—球与滚道之间的相对平均速度;Rx—当量曲率半径;G—无量纲材料参数。

在求出油膜厚度后,笔者将其代入以上各式,即可计算出油膜的刚度。

在以上各式中:式(22)适用于球和套圈滚道,式(23)适用于球和兜孔,式(24)适用于内圈,式(25)适用于外圈。

1.3.3 等效综合刚度计算

接下来进行等效综合刚度的计算。

等效综合刚度的计算式为:

(27)

式中:Kj—球与其点接触物体的接触刚度;Ky—球与其点接触物体之间的油膜刚度。

通过上式计算得到的综合刚度,即为考虑弹流润滑后的球与各部件之间的综合接触刚度。

2 仿真及结果分析

因为浪型保持架由球引导,不稳定因素较强,所以球与保持架之间的相互作用可视为随机激励。对于该种随机过程,一种较为普遍的处理方法是研究其某些“统计规律性”,故其仿真总体时间的设定也是研究裂纹故障的重要因素。时间较短,则会导致所分析的样本函数仍具有一定的随机性;时间过长,则会导致某些时刻因故障产生的激励被较大的数据量所掩盖。

故在3种转速下的时间选取上,笔者都以保持架旋转80圈左右为标准,且其截取的数据均为保持架进入“稳态”以后的数据。在保持架的加速过程中,其动态性能则不在本文考虑范围之内。

2.1 质心轨迹的分析

由于各裂纹情况除断裂外并无较大差别,此处只展示正常(裂纹深度0 mm)、裂纹(裂纹深度0.7 mm)以及断裂(裂纹深度1.75 mm)3种情况下裂纹保持架的质心轨迹。

在径向载荷200 N与重力场作用下,各裂纹深度与转速对保持架质心轨迹的影响,如图1所示。

图1 不同裂纹保持架质心轨迹演化图

由图1可以看到:

(1)在轴承径向力的作用下,保持架质心先向Z轴负方向偏移(Z轴负方向为重力方向与径向载荷施加方向),并在较高转速下,由于离心力的作用开始向一侧偏移;

(2)该型号球轴承由球引导,因为径向游隙与保持架兜孔间隙的存在,故而其保持架质心轨迹为在一定的椭圆范围内不规则的涡动;

(3)在同一转速下,由于裂纹的存在使得保持架质心的涡动范围不断增加,且这一特征随着转速的升高变得越来越明显;

(4)随着转速的升高,裂纹保持架质心涡动轨迹相较于正常保持架的变化趋势保持一致,断裂的保持架则明显不同于前正常和裂纹保持架。

2.2 保持架转速的分析

对于各深度裂纹在各内圈转速下的保持架转速,通过观察其概率密度函数(PDF)图,可以更清晰地观察到各种参数值的变化[16,17]。

不同裂纹深度下,保持架转频的概率密度函数如图2所示。

图2 不同裂纹保持架转速PDFs

为便于观察,保持架转频的跨度此处均设为5 Hz。对于正常保持架3个内圈转速,与无故障保持架经验公式求得的保持架理想转速的误差分别为2%、1.1%、1.3%。该结果说明了所搭建模型具有一定的合理性。

由图2可看出:

(1)在40 Hz和100 Hz的内圈转频下,保持架的各项参数指标及转速分布情况均与正常状况有所差异,但并不能清晰地表达保持架的故障,这一点的敏感性差于质心涡动轨迹;

(2)在200 Hz的内圈转频下,断裂情况下的保持架转速分布情况发生了明显的改变。此时若是把平均转速这一参数作为识别轴承故障的依据,相对于裂纹保持架,断裂保持架的转速降低1.4%左右,敏感性较差,但在概率密度函数图上仍可以清晰地捕捉到这一改变(发生这种变化的原因为:保持架断裂后,对球的周向保持作用下降,同时因保持架断裂自身产生不平衡力,使得球在滚道内产生窜动。球的不稳定也使得球对保持架的引导处于失衡状态,导致保持架公转速度降低)。

2.3 球与保持架的碰撞分析

保持架与球频繁的碰撞是造成疲劳裂纹的主要因素,故而了解保持架与球碰撞的规律至关重要。

在正常、裂纹和断裂情况下,在保持架公转1周的过程中,相同的2颗球(故障保持架选取裂纹两侧的球)与保持架兜孔的接触力,如图3所示。

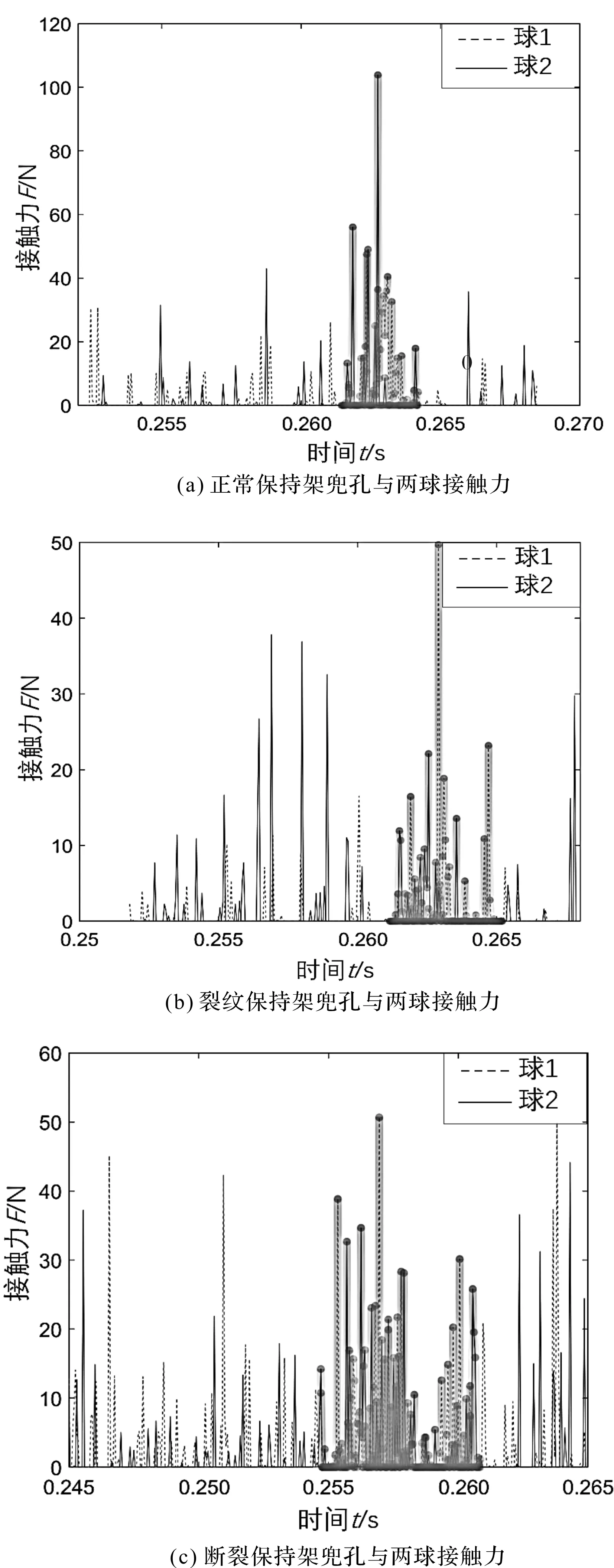
图3 保持架兜孔与两球接触力图

从图3可以看出:在旋转1周的过程中,断裂保持架与球的总碰撞次数,明显多于正常裂纹保持架和球的总碰撞次数,且在线条加粗的时间段内(对应图4中0°～90°),其碰撞次数明显比其他时间段更多;裂纹保持架与两球的碰撞次数在图示的所有时段均明显要高于正常的保持架。

与受力图中的线条加粗区域相对应,保持架与两球频繁碰撞的区域,如图4所示。

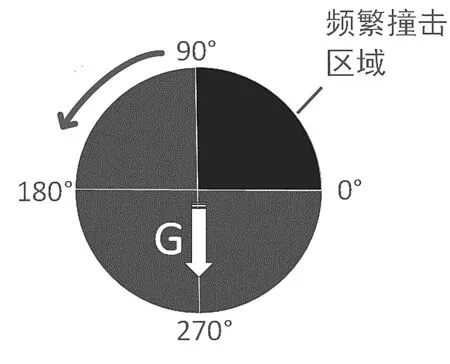
图4 保持架与球频繁撞击区示意图

结合图(3,4)可以看出:保持架与球频繁接触的区域不在承载区,而在沿旋转方向从0°～90°的过程区域。其原因是:在承载区,套圈与球的作用力为主导;在脱离承载区以后,球沿90°～180°运转过程中开始与重力方向(本文模型Z轴负方向)相反,导致球的速度变慢,从与保持架发生频繁碰撞。

保持架与球发生碰撞会导致其速度改变,这一现象反映在图上即为曲线斜率的改变。

在频繁碰撞区,保持架的速度变化曲线如图5所示。

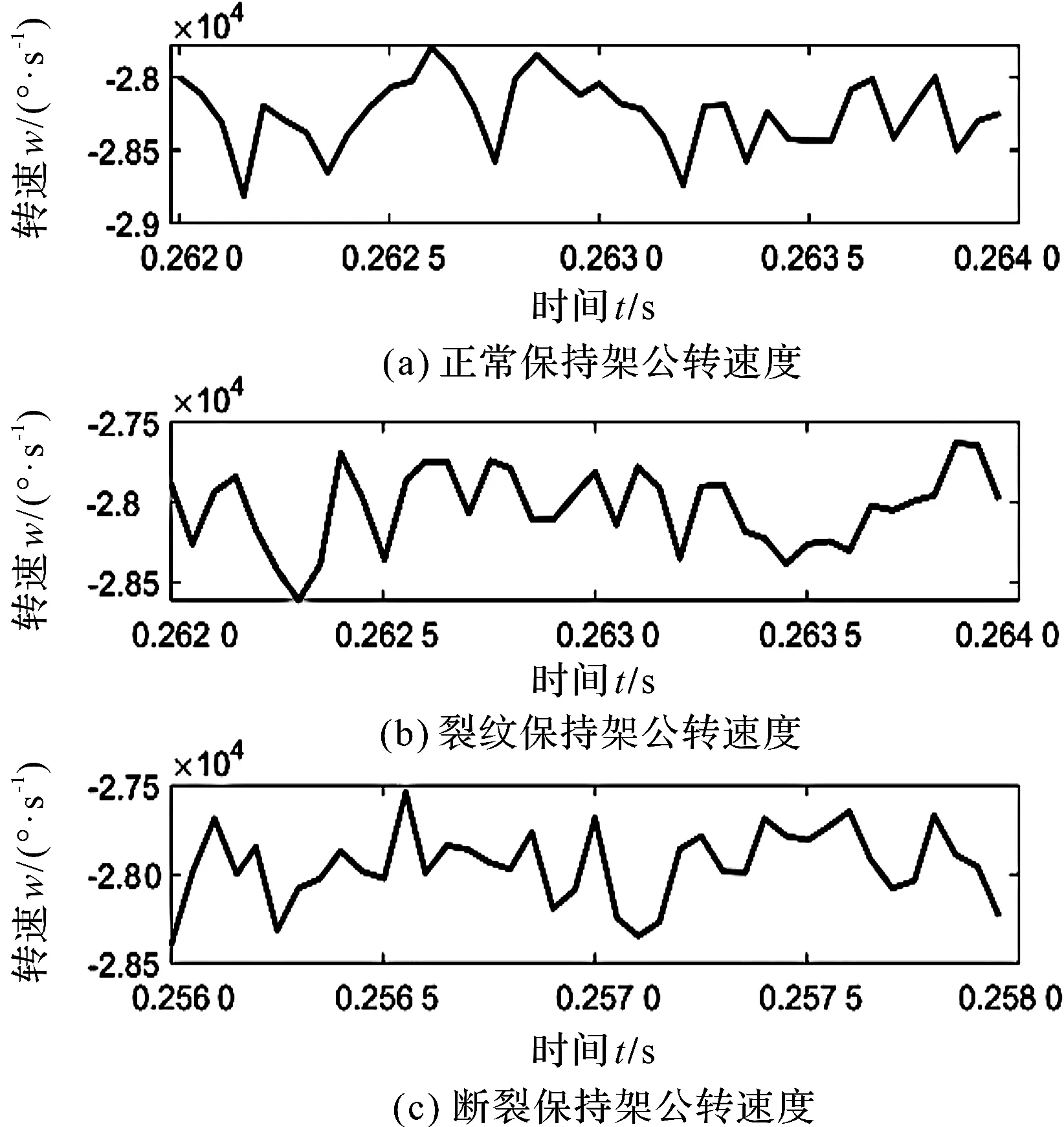
图5 保持架公转速度图

由图5可知:在相同时间的步长内,斜率改变的次数随着裂纹深度的增加而增加,分别为27次、34次、35次。这一改变说明,保持架在出现裂纹故障后,相同时间步长内的碰撞次数明显增加;

同时,结合图3也可知:两球与断裂保持架兜孔频繁碰撞的时间比裂纹保持架的更长。

由此可以得出结论,即在保持架疲劳裂纹萌生以后,会因为以上的原因而使裂纹快速扩展。同时,这也是在工程实际应用中,多数保持架故障被发现时已经是到了断裂状态(晚期)的原因。

3 结束语

笔者通过多体动力学仿真软件ADAMS对不同裂纹深度下的柔体保持架进行了动力学仿真,得到了不同裂纹深度下保持架的质心涡动轨迹、转动速度的概率密度函数、球与保持架的频繁撞击区域,以及球和不同裂纹深度的保持架的碰撞规律,得到了裂纹扩展过程中,保持架动态特性的改变以及不同维度的表现形式。

研究结果表明:

(1)浪型保持架质心涡动轨迹范围随着裂纹程度的加深而增大;

(2)在内圈高转速且保持架断裂时,从浪型保持架转速的概率密度函数图可清楚地观测到其差异,在其余情况下则敏感性不强;

(3)浪型保持架与球碰撞最频繁的区域不在承载区,而在沿旋转方向的逆重力方向,且当出现裂纹时其碰撞次数要显著多于正常情况时,这些因素也是造成保持架裂纹扩展的主要原因。

在后续的研究中,笔者将针对球轴承浪型保持架,应用电涡流传感器以实现对球轴承保持架质心涡动轨迹及转速等变量的测量,达到在线监测保持架裂纹故障的目的。