基于阀芯结构优化的比例阀液动力补偿方法研究*

白 俊,赵 斌,郝云晓,王 波,刘 赫

(太原理工大学 新型传感器与智能控制教育部与山西省重点实验室,山西 太原 030024)

0 引 言

直动式比例阀是比例控制技术的核心元件。在直动式比例阀的工作过程中,由阀内比例电磁铁输入电信号,使比例阀的阀芯产生相应的动作。在这一过程中,阀芯主要受到驱动力、惯性力、摩擦力、弹簧力和液动力共5个力的共同作用。

在阀芯受到的所有力中,最难准确计算的就是液动力。由于比例电磁铁提供的驱动力有限,过大的液动力会导致阀芯产生卡滞现象。所以,研究阀芯所受液动力的规律和补偿方法,对提高直动式比例阀工作性能有着重要作用。

在针对阀内流场及液动力的研究方面目前已有很多的成果。金伟等人[1]采用FLUENT对旋转阀进行了仿真分析,得到了旋转阀不同旋转角度下的速度、压力及基曲线图,可为旋转阀的优化设计提供理论参考。张鑫等人[2]利用FLUENT软件,得到了多路阀动臂联稳态流场的内部流动规律和稳态液动力的变化规律,该结果可为多路阀的优化设计提供参考。赵蕾等人[3,4]利用动网格技术,分析了全周开口滑阀所受的液动力及其径向不平衡力。扬科等人[5]采用FLUENT中的动网格技术,针对0.5 mm小开口滑阀的流动状态进行了静、动态仿真,研究了小开口滑阀的流量及其液动力特性。杨庆俊等人[6-8]针对不同的节流槽及流道结构进行了仿真研究,分析比对了不同类型的节流槽及不同尺寸的流道结构对稳态液动力的影响。郑长松等人[9]应用FLUENT仿真软件,在考虑了轴颈对液动力影响的基础上,分析了滑阀在不同开度下的流场与稳态液动力的变化规律。

由于以上的研究工作缺少相关实验数据作为参照,张宏等人[10]采用了实验与仿真相结合的方法,对滑阀的稳态液动力进行了仿真,结果发现,在滑阀的稳态液动力仿真中,采用k-ε模型能够更好地拟合试验数据。

目前,针对滑阀的稳态液动力的补偿方法主要有:改变流道布置法[11]、阀套斜孔法[12]及非全周开口法[13]。同时,国外学者RICCARDO A等人[14-18]通过优化阀芯结构,有效地降低了滑阀的稳态液动力。

以上研究大多只针对比例阀的进油口,而在实际工程中,比例阀的进油口和回油口是同时工作的。

结合上述关于滑阀液动力的研究方法,笔者探讨开度在0～1.0 mm阀套上开矩形通孔的滑阀,在不同开度及压差时的液动力大小,并分别对滑阀进油口和回油口的阀芯结构进行优化;同时,分析全流域工况下,阀芯结构优化对其液动力补偿的效果。

1 直动式比例阀工作原理

直动式比例阀是一种常见的、应用范围广泛的液压控制装置。通过比例电磁铁,直动式比例阀可以按输出电信号连续、按比例地对油液的压力、流量和方向进行控制。

直动式比例阀的结构如图1所示。

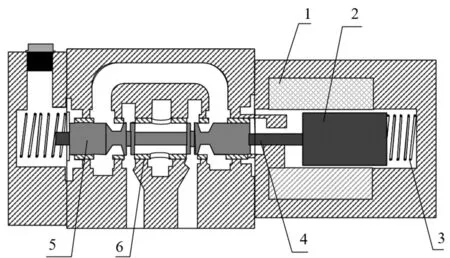
图1 直动式比例阀结构图1—线圈;2—衔铁;3—推杆;4—弹簧;5—滑阀阀芯;6—阀套

图1中,当线圈1接通电信号时,线圈内产生磁场,对衔铁产生作用力,衔铁2在磁场中按信号电流的大小和方向成正比例、连续地运动,再通过推杆3控制滑阀的阀芯运动。

在阀芯的运动过程中,阀芯的受力公式为:

(1)

式中:Fact—电磁铁所提供的驱动力;m—直动式比例阀阀芯、电磁铁衔铁及弹簧的质量之和;b—阀芯运动时的等效粘性阻尼系数;Fpk—弹簧作用力;F1—直动式比例阀阀芯所受液动力;Fpf—直动式比例阀所受的摩擦力。

由式(1)可知:

(1)在比例阀的工作过程中,电磁铁的输出力需克服弹簧力、液动力和摩擦力等阻力。在这些阻力中,摩擦力较小,其对比例阀的动、静态特性影响也较小;

(2)弹簧输出力与其自身刚度和阀芯位移有关,基本不受阀口压差和流量变化的影响,因此,其对比例阀的动、静态特性影响基本不变。

在比例阀的工作过程中,阀芯液动力随阀口压差和流量的增大而增大。由于比例电磁铁自身驱动能力有限,当比例阀在高压、大流量工况下工作时,阀芯所受液动力较大,阀芯响应速度过慢,比例电磁铁输出力不足以推动阀芯运动。

而阀芯所受到的液动力是限制直动式比例阀工作压差、通流能力,及影响比例阀动态特性的关键因素。因此,研究如何减小阀芯所受到的液动力,对提升直动式比例阀的性能具有重要意义。

2 计算模型处理

2.1 分析模型处理

此处以某型号6通径直动式比例阀作为研究对象,其结构如图2所示。

图2 比例阀整体结构示意图

在直动式比例阀中,为了获得良好的性能,通常采用阀套与阀芯组合的形式,同时便于阀套上节流槽的加工。图2中,阀套上就加工有矩形节流槽。

同时,在图2中,油液由P口经节流槽流向A口,油液由B口经节流槽流向T口。

设定额定压差为3.5 MPa、额定流量为24 L,笔者对阀套节流槽进行设计;初步计算得到阀套矩形节流槽的通流面积为7.5 mm2;设计比例阀阀芯行程为1 mm,在阀套上设计2个对称的矩形节流槽,节流槽面积梯度为3.125 mm。

首先,笔者采用UG软件,对该直动式比例阀结构进行三维建模。

比例阀的滑阀三维模型如图3所示。

图3 比例阀的滑阀三维模型图

2.2 网格划分

笔者将建立的三维模型导入ANSYS/DM中,抽取其流道。

在对模型进行网格划分时,为了控制网格数量,提高计算的效率,此处只对阀套节流口处进行网格细化,并保证在阀口尺寸最小的地方有5个网格(比如开口度为0.2 mm时,阀口处网格大小为0.04 mm)。

P-A进油口流体域三维网格模型如图4所示。

图4 直动式比例阀三维网格模型

2.3 边界条件和计算条件

此处,将边界条件设置为:

油口P为压力入口,油口A为压力出口;其余壁面设置为静止壁面,整个实体区域设置为流体区域。

计算条件设置为:

(1)流体为牛顿流体,且不可压缩;

(2)假设阀芯与阀套之间无配合间隙;

(3)液体介质选用46号液压油,其密度为ρ=890 kg/m3,动力黏度为μ=0.046 kg/(m·s);

(4)流动状态为湍流,采用k-ε湍流模型。

3 比例阀CFD仿真分析

3.1 直动式比例阀流场分析

此处取阀口压差为12 MPa,此时,笔者通过FLUENT软件对不同阀口开度进行仿真计算,得到阀口及流道的压力和速度流线分布结果。

这里以阀口开度1.0 mm为例,经过仿真得到常规滑阀流场分布图,如图5所示。

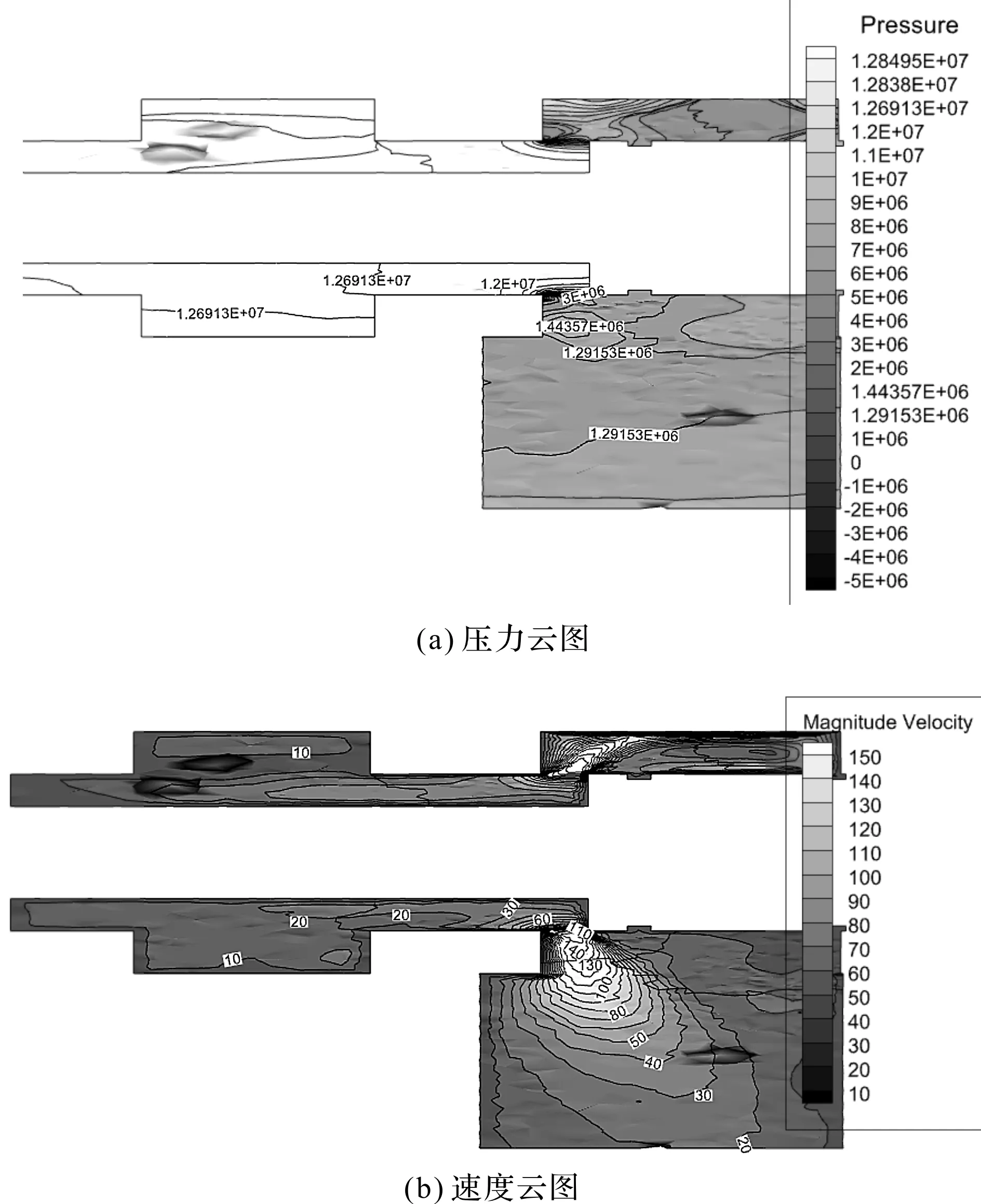
图5 常规滑阀流场分布图

从图5中可以看出:

(1)当油液流经阀口时,由于阀口起一定的节流作用,导致流经阀口的流速增大,此时,在阀口处形成高速射流区;

(2)最高流速出现在高速射流的中心区域,此处油液压力迅速降低,并出现局部负压区,导致流体空化现象的发生。

3.2 稳态液动力

当阀口的开度一定时,油液流经滑阀时其流速的大小和方向均发生变化,对滑阀产生一个反作用力,该力作用在阀芯上,其轴向分量即为稳态液动力。

滑阀稳态液动力的理论表达式为:

F=2CVCdAaΔpcosθ

(2)

式中:CV—流速系数,一般取值为0.95～0.98;Cd—流量系数;Aa—阀口通流面积;Δp—阀口前后压差;θ—滑阀节流口处的射流角,对于理想滑阀,一般取θ=69°。

笔者采用FLUENT软件,对比例阀不同阀口开度及压差下阀芯所受的液动力进行仿真计算,得到稳态液动力的仿真值,并将其与通过式(2)计算得到的液动力理论值做对比。

不同压差与阀芯位移时,比例阀稳态液动力的变化曲线,如图6所示。

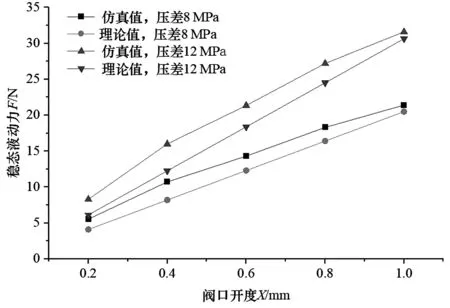
图6 不同压差与阀芯位移时比例阀稳态液动力变化曲线

对图6所示的理论与仿真曲线进行分析可知:

(1)阀芯所受液动力都是随阀口开度和阀口压差的增大而增大,当阀口开度大于一定值时,仿真获得的阀芯稳态液动力变化速率明显减小;

(2)在理论计算过程中,将射流角、流量系数和流速系数等取为定值,阀口压差固定;阀套采用矩形节流通孔设计,通流面积和阀口开度成正比;理论计算获得的比例阀液动力与阀口开度成比例关系。

然而,阀芯稳态液动力为作用于台肩壁面的压力合力,而台肩壁面所受压力与阀腔尺寸等因素相关,它们之间没有线性关系,所以仿真获得的稳态液动力与阀口开度的变化关系曲线并不是一条直线。

3.3 阀芯结构优化设计

3.3.1 改进结构原理

由于本质上阀芯液动力是由流过阀口的流体动量变化引起的,此处可采用阀腔控制体的动量变化来表示阀芯的液动力。

P-A原结构和改进结构示意图如图7所示。

图7 P-A口示意图

根据动量定理,液动力的计算公式为:

F=ρQ(v1cosθ1-v2cosθ2)

(3)

式中:v1，v2—流体流入和流出阀口的平均速度;θ1，θ2—流体流入和流出阀口的角度。

由于阀口处无倒角、圆角,且无配合间隙,此时的出射角θ2=69°,入射角θ1=90°。

由式(3)可知:要想减小液动力可以采用减小入射角的方法,这里通过在阀杆中间增设锥形凸台的方法,来改变流入阀口的速度方向,以减小入射角的大小;并且在阀芯台肩根部增加圆角,以获得更好的导流效果,减小对阀芯台肩根部造成冲击(图7)。

图7(b)中,锥形凸台的高度与阀芯台肩平齐,由于出射角θ2=69°,这里将凸台斜角α设为21°,倒角R=1 mm。

3.3.2 结构改进后对液动力及流量的影响

在不同压差下,笔者对优化后的滑阀结构在不同开口度下的液动力进行三维流场仿真分析,以得到滑阀阀芯所受的液动力和进出口流量。

优化前后，不同滑阀结构的液动力曲线如图8所示。

图8 不同结构液动力曲线

优化前后，不同滑阀结构的流量曲线如图9所示。

图9 不同结构的流量曲线

由图9可以看出:

(1)阀口流量随阀口开度和压差的增大而增大,流量与阀口开度近似成线性关系,该结果表明,阀套开矩形节流口这种结构使其具有良好的线性特性;

(2)改进结构后阀口的流量曲线近似与原结构阀口流量曲线重合,这表明优化的锥形凸台对流量造成的影响很小。

由图8、图9可以看出:当阀口开度较小及流量较小时,改进结构对滑阀液动力的补偿效果并不明显;但随着阀口开度、流量和压差的不断增大,结构优化对阀芯液动力的补偿效果则越来越明显。

3.3.3 锥角α对液动力的影响

由式(3)可以看出:理论上,当入射角θ1越小,即锥形凸台的倾斜角α越大时,式中液动力F值越小。

根据前述分析可知,液动力随阀口开度和压差的增大而增大,这里选取压差为12 MPa,开口1.0 mm的工况下,不同锥台斜角α(α分别取11°、21°、31°、41°、51°、61°)进行仿真分析。

在不同凸台倾斜角下,稳态液动力的变化结果如图10所示。

图10 稳态液动力在不同凸台倾斜角下的变化

图10中,随着凸台倾斜角的不断增大,稳态液动力的值不断减小,由此可见,仿真结果与理论公式分析的结果相符。

由于受到阀芯尺寸的限制,在本研究中,凸台倾斜角α设置为61°。此时,阀芯的液动力已经很小。

3.4 全流域的液动力分析

3.4.1 回油口结构改进

改进前后的回油口B-T结构对比图,如图11所示。

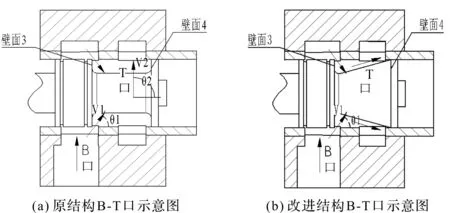
图11 B-T口示意图

图11中,原结构回油口结构模型的阀口处无倒角、圆角,且无配合间隙,此时的入射角θ1=69°,出射角θ2=90°。由前文可以得出结论,要想减小液动力,应尽量减小出射角θ2。

因此,在改进后的结构中,笔者将壁面4设计成锥面;锥面斜度应取较大值,以满足出射角θ2尽量小的条件;而且,更大的锥面斜度也有利于减小油液对原壁面4的冲击。

3.4.2 全流域仿真模拟

优化前后的阀芯模型如图12所示。

笔者分别对原阀芯结构和优化后的阀芯结构进行了全流域的流场仿真,得到的全流域流体域计算模型如图13所示。

图13 全流域流体域计算模型

然后,笔者将油口A和B用管路相连,P口为进油口,T口为出油口。

在仿真过程中,笔者取进油口压力值为12 MPa、18 MPa、24 MPa,取出油口压力值为0 MPa分别进行模拟。

模拟得到不同结构全流域液动力仿真曲线如图14所示。

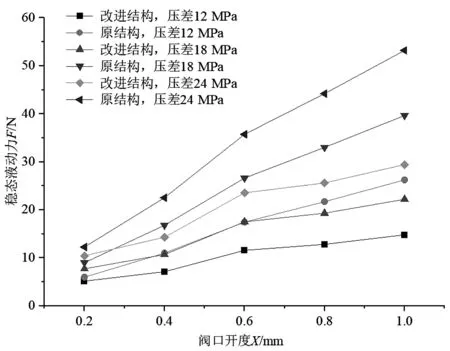
图14 不同结构全流域液动力仿真曲线

由图14可以看出:采用优化后的阀芯,能够明显地减小阀芯的液动力;在比例电磁铁自身驱动力有限的条件下,可以避免由于阀芯所受液动力过大而造成阀芯响应速度慢的问题;

同时,与改进结构相比,原结构在小开口处液动力差异很小,且差异随着阀芯开口度和压差的增大而增大,液动力最大补偿效果可达45%。

以上仿真结果表明:通过对阀芯结构进行优化[19,20],可在大开口、大流量、大压差的工况下,很好地补偿阀芯的液动力。

4 结束语

笔者以开矩形阀套节流通孔的滑阀阀腔为研究对象,分析了滑阀阀芯所受的稳态液动力、随阀芯的开口度以及压差变化的规律,提出了一种阀芯结构的优化方法,实现了对滑阀阀芯所受稳态液动力的补偿。

主要研究结论如下:

(1)通过理论分析与仿真研究,发现稳态液动力理论计算结果与阀的开口度、压差成线性关系(仿真获得的稳态液动力与阀口开度关系并不成比例关系),并且随着阀的开口度的增大,比例系数不断减小;

(2)依据理论公式提出的阀芯结构优化方法,可有效地减小阀芯所受的稳态液动力,且不会对滑阀流量特性造成影响;优化后的阀芯结构锥面斜度越大,液动力补偿效果越好,并且在高压、大流量的工况下,液动力的补偿效果更明显。

在后续的研究工作中,笔者将研制出直动式比例阀的样机,并通过对其特性的测试,来验证上述阀芯结构优化方法的可行性和效果。