基于SDP和DG-ResNet的齿轮箱轴承故障诊断研究*

韩春雷,武 兵,2*,熊晓燕,2,任俊锜,刘智飞

(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.太原理工大学 新型传感器与智能控制教育部重点实验室,山西 太原 030024)

0 引 言

齿轮箱是机械设备中实现动力传递,调节运行速度的重要部件。在一些工业生产过程中,机械设备运行环境恶劣,随着机械设备长时间、高强度的工作,齿轮箱轴承成为了某些机械设备运行最主要的故障源,因此对齿轮箱的轴承进行故障诊断十分必要。

目前,齿轮箱轴承的故障主要通过传统的数据驱动进行诊断,传统诊断方法占用了大量人力和资源,且效果较差。

近年来,随着计算机软、硬件能力的提升以及各种数据集的开源化,深度学习得到了快速的发展,大数据给传统的故障诊断技术带来了巨大的挑战和颠覆性的创新[1]。

为实现故障诊断的智能化,以及能够自动提取出故障的特征,深度学习随之被运用到了齿轮箱轴承故障诊断领域[2]。

CHEN Zhi-qiang等人[3]将振动数据的时频特征作为CNN输入,实现了对齿轮箱的故障分类。李思琦等人[4]将故障数据用EEMD进行了分解,得到了本征模态函数,再将其作为CNN的输入,实现了对滚动轴承故障进行有效的分类诊断。王鹏飞等人[5]将数据用小波分解,然后对其进行了EMD模态分解,得到的信号再通过包络谱分析,实现了对轴承的故障诊断。王海林等人[6]首先用小波分析方法对轴承的故障数据进行了去噪处理,然后将其输入到RBF神经网络中,实现了对轴承故障的分类。王新等人[7]首先使用VMD处理轴承故障的原始数据,将得到的分量作为SVM输入,实现了对轴承故障的分类。任雪平等人[8]将轴承振动数据采用小波包和奇异值分解(SVD)的方法进行了处理,然后再将其输入到经过粒子群算法优化的BP神经网络中,最终实现了对滚动轴承的故障分类。

但是,在采用上述数据处理方法对原始数据进行处理时,原始数据会产生一定的损失;同时,传统分类器和CNN网络的故障诊断准确率不够高,难以满足现实中对故障分类的要求。而卷积神经网络可以学习到图像的细微特征,从而提高对输入图像的识别率。

为了解决轴承故障分类过程中原始数据损失大、分类效果差等问题,本研究提出基于SDP和DG-ResNet的轴承故障诊断方法。首先,将采集的一维故障数据通过SDP算法转化为二维故障图像,然后用DG-ResNet对故障图像进行特征提取和分类,以实现对齿轮箱轴承的故障分类。

1 基于SDP和DG-ResNet的故障诊断模型

笔者使用对称点图像(SDP)算法技术,将一维的轴承故障振动数据转化为二维图像(图像可以充分显示出故障信息),DG-ResNet网络模型可以提取输入数据的高维度特征,从而实现对轴承故障的分类。

笔者提出的基于SDP和DG-ResNet的故障诊断流程如图1所示。

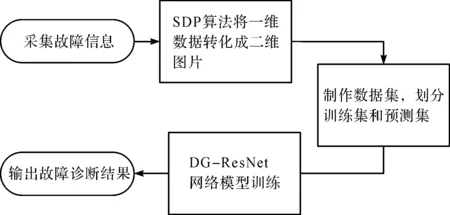
图1 基于SDP和DG-ResNet的故障诊断模型流程图

1.1 SDP算法

1.1.1 算法原理

SDP算法[9]是通过归一化的方法,将不同故障的时间序列信号映射到极坐标上,从而产生SDP图像。不减少数据前提下,经SDP算法转化后的图像可以直观地展现出不同故障的极值与变化情况。

SDP算法的原理如图2所示。

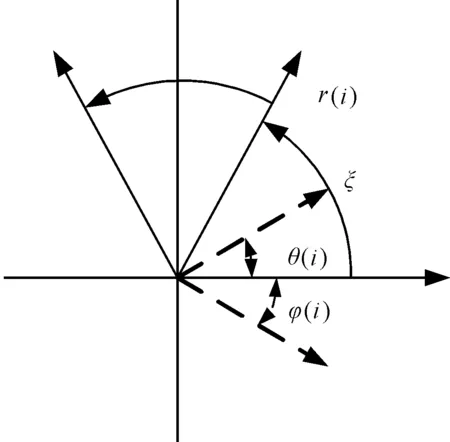
图2 SDP算法原理r(i)—极坐标半径;ξ—放大系数;θ(i)—逆时针偏转角度;φ(i)—顺时针偏转角度

时间序列的每一个点都会映射到极坐标轴上,这种映射关系如下:

(1)

(2)

(3)

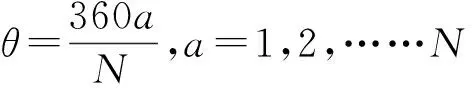
1.1.2 SDP图像特征及参数选择

因故障的不同,SDP图像特征也会有所不同。在SDP图像中,不同的故障信号主要表现为以下几方面[10]:(1)SDP特征图像的几何中心;(2)SDP特征图像的曲率;(3)SDP特征图像的集中区域;(4)SDP特征图像的形状大小以及薄厚。

SDP算法可以同时使用多通道信号进行图像转化,每一个镜像对称面可以表达一组时序信号的信息,将同一设备的多信号通道同时进行SDP转化,可以更有效地挖掘设备的故障信息,及时地发现故障源。

SDP算法在实现前需要对核心参数进行选择,首先是对称角度θ,由于本研究的数据集是使用2个三轴加速度传感器采集的六通道振动信号,笔者选择θ值为360°/6=60°。

最终,得到的SDP图像为6瓣,每瓣的对称轴分别为60°、120°、180°、240°、300°、360°。

其次是时间滞后系数a,通过实验可得a=1。

1.2 膨胀-组卷积残差网络

1.2.1 组卷积

卷积是神经网络运算的核心,其主要功能是特征提取。卷积层主要是提取输入数据的特征,卷积核用来计算不同的特征图[11]。激活函数是在卷积计算后进行非线性处理,以便于有效地防止过拟合。

本研究使用ReLU激活函数,其卷积计算如下:

(4)

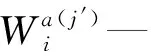
ReLU激活函数为:

f(x)=max(0,x)

(5)

分组卷积(grouped convolution)是将多组卷积并联运行[12]。分组卷积计算示意图如图3所示。

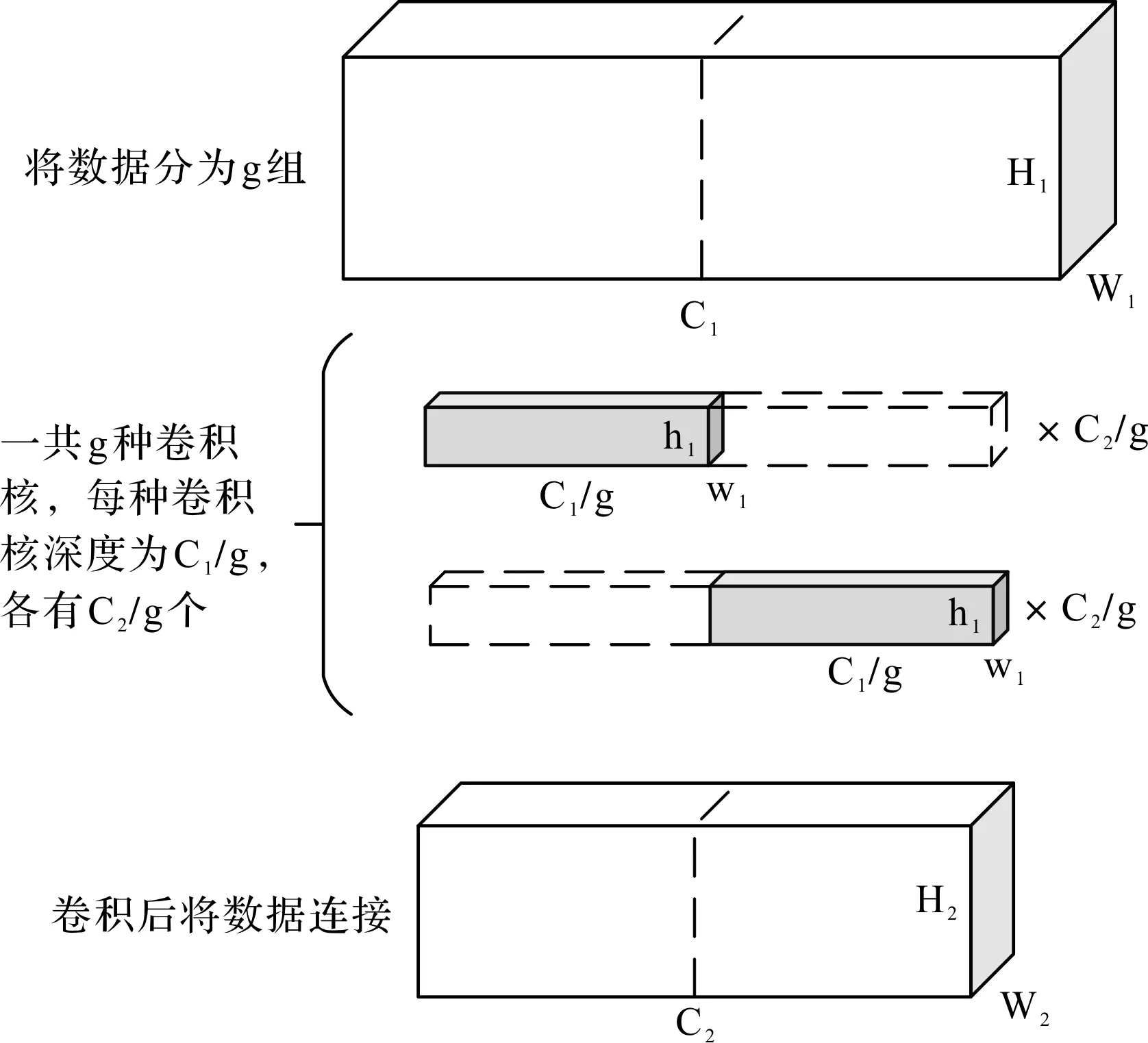
图3 分组卷积计算示意图

图3中:分组卷积是将数据按照数据深度分成g组,即每组数据量为(C1/g)。由于数据量减少,原始卷积核的大小不变,通道数变成了(C1/g),同时每组的卷积核的个数变为(C2/g)。

在卷积结束输出结果前,要将各组数据连接起来,最终的输出通道依旧是C2,这样可以保证输出通道与普通卷积无变化,但组卷积对数据特征提取能力更强。

1.2.2 膨胀卷积

膨胀卷积[13](dilated convolution)是指在普通卷积核中间加入空洞,以0填充,目的是为增大感受野的范围。与普通卷积相比,膨胀卷积在参数数量上没有变化,但是其感受野更大,能学习到更多的图像特征信息。

卷积核膨胀计算公式为:

F=α×(k-1)+1

(6)

式中:F—膨胀卷积核大小;α—膨胀系数;k—原始卷积核大小。

膨胀卷积计算公式为:

out_k=(in_k-F+2×P)/S+1

(7)

式中:out_k—输出图像大小;in_k—输入图像大小;F—卷积核大小;P—图像边界0填充个数;S—卷积核移动长度

1.2.3 残差网络

网络越深,对特征的提取能力就越好,当层数到达一定程度时,再加深网络的层数,准确率反面会大幅降低。为了解决因神经网络加深而引起的网络退化问题,HE Kai-ming等人[14]提出了一种残差神经网络。

残差网络的残差块如图4所示。

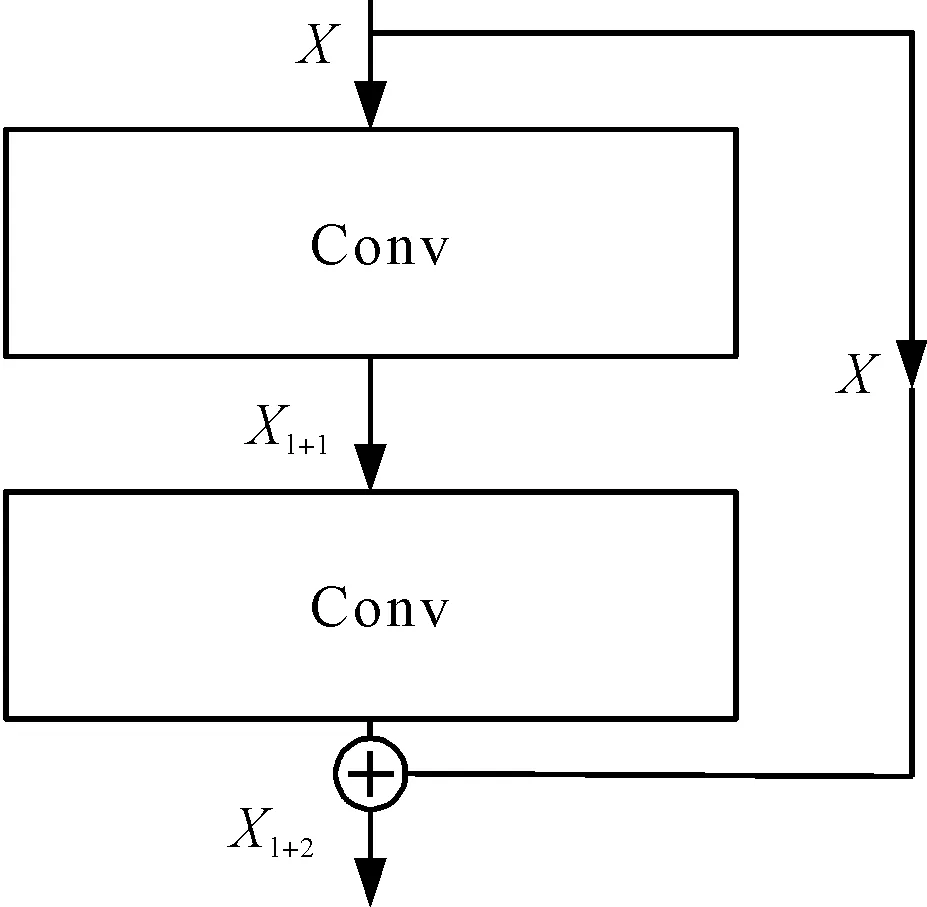
图4 残差块结构

图4中,把X作为输入,经过卷积、池化、激活函数操作,得到新的输出Xl+1,再将经过卷积操作后的Xl+1与最开始的输入X用shortcut相连接,经过激活函数操作得到新的Xl+2,从而构成一个完整的残差块。

残差块可以学习到之前输入的特征,从而减少信息的丢失;还可以实现恒等变换和反向传播时有梯度传递,有效减小梯度爆炸和消失现象。

残差块的计算公式为:

(8)

Xl+1=g(fl+1(X))

(9)

(10)

(11)

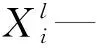
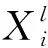
1.2.4 膨胀-分组卷积残差网络结构模型

该网络通过多组膨胀-分组卷积残差块,对输入的图像进行特征提取。随着网络深度的不断加深,网络模型的泛化能力更强。

模型的整体结构如图5所示。

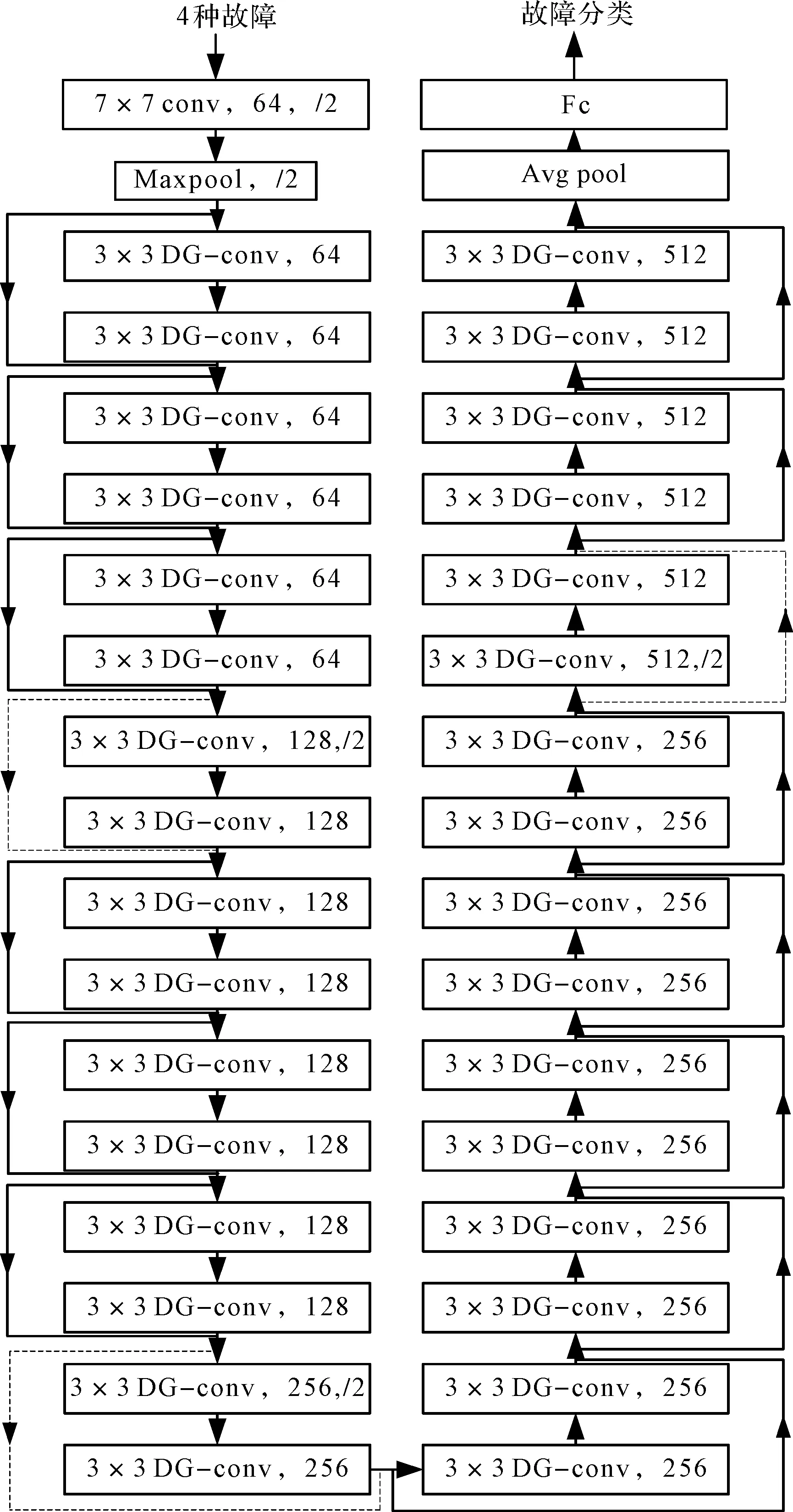
图5 膨胀-分组卷积残差网络结构模型

由图5可知:DG-ResNet由多个膨胀-分组卷积残差块组成,其中,通道数64、128、256、512分别代表4种不同的残差块结构。

膨胀-分组卷积将膨胀卷积加在分组卷积上,有两个作用:(1)膨胀卷积以分组卷积为载体,增加了分组卷积的个数,同时也增加了膨胀卷积的个数,以利于对输入图像进行特征提取;(2)分组卷积以膨胀卷积为依托,在不增加分组卷积参数的前提下,增大了分组卷积的感受野,使得网络可以学习到更多的特征。

膨胀-分组卷积残差块是使用残差连接的方式将膨胀-分组卷积连接起来,其在加深网络层数的过程中,可以有效地减少过拟合现象的发生。

其步骤是:首先将一维故障振动数据使用SDP方法转化后,将故障图像作为网络输入(输入图像是3通道的RGB图像);经过步长为2的7×7的卷积和2×2的最大池化预处理后,输入到通道数为64的膨胀-分组卷积残差块中;在经过6个填充为1的3×3膨胀-分组卷积处理后,预处理特征图的尺寸大小没有发生变化,由于输出通道数都是64,残差块实线连接;经过64通道的膨胀-分组卷积残差块处理后的特征图,作为通道数为128的膨胀-分组卷积残差块输入;

特征图首先经过填充为1、步长为2的3×3膨胀-分组卷积操作,特征图尺寸减小为输入的一半,通道数变为128。由于该残差块的输入和输出通道数不同,要对输入特征图添加1×1×128的卷积转换,图5中不同通道数交界处残差块需虚线连接,表示需要转换通道数。随后再经过7个通道数为128、填充为1的3×3膨胀-分组卷积处理后的特征图,作为通道数为256的膨胀-分组卷积残差块的输入;

特征图分别经过12个通道数为256、填充为1的3×3膨胀-组卷积和6个通道数为512、填充为1的3×3膨胀-分组卷积处理,处理过程和通道数为128的顺序一致,只是通道数不同。最后,输出的特征图通过展平处理后作为分类器的输入,从而实现4种故障的分类。

该网络模型有3个特点:

(1)除第一个通道数为64的膨胀-分组卷积残差块外,其余通道数残差块的第一个膨胀-分组卷积操作,都需要将步长设置为2,以减小特征图尺寸,同时增加通道数,让DG-ResNet更好地提取高阶抽象特征;

(2)相同通道数残差块内部卷积操作不改变特征图尺寸;

(3)不同通道数交界处膨胀-分组卷积残差块需将输入通道数转化为输出通道数,以实现残差块相加。

2 实验验证

2.1 实验台

为了验证所提出的基于SDP和DG-ResNet轴承故障诊断模型的有效性,此处笔者采用来源于HD-CL-012X行星齿轮箱试验台采集到的轴承故障数据。

HD-CL-012X行星齿轮箱实验台如图6所示。

图6 HD-CL-012X行星齿轮箱实验台

图6中,实验台从左到右依次是电机端、转速传感器、行星减速机和磁粉制动器。

本研究使用DEWESoft7.0软件采集了2个三轴加速度传感器数据,传感器是PiezoStar®微型加速度计-8766A050,选用了在300 r/min、600 r/min转速下,3种负载(A=1.5 n·m、B=3 n·m和C=5 n·m),采样频率为5 kHz,采样时间为60 s的数据。

实验轴承使用6212轴承,轴承内径是60 mm,外径是110 mm,厚度为22 mm。

传感器采集轴承端盖的故障信号。故障共有3种类型:(1)NWQHHDS—轴承内外圈混合点蚀;(2)ZCNL—轴承内圈裂纹;(3)ZCWL—轴承外圈裂纹。ZC表示正常轴承。

2.2 实验数据

行星齿轮箱内部只包含两个同种型号的6212轴承,每次实验使用其中一种故障轴承做实验,故障轴承放置在远离电机一端,同时两个传感器分别放置在轴承端盖侧面与上面,每个传感器采集每种状态下x、y、z3个方向的振动信号,以及2个传感器共6个通道的数据。采集完一种后更换下一种故障轴承,采集到的正常数据与3种故障数据一共为4种数据类型。

定义每1 000行、6通道数据作为一个样本,每种数据类型获得900个样本,按照9:1的比例将数据集分成训练集和测试集。最终,实验数据集中的训练集有6 480个样本,验证集中有720个样本。

实验数据样本如表1所示。

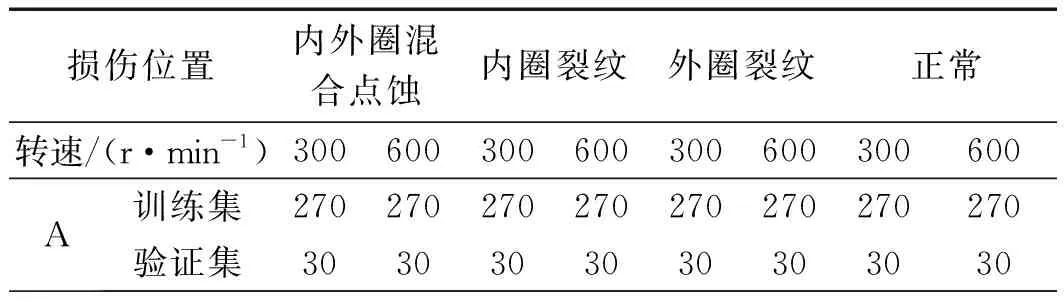
表1 实验数据样本

续表

2.3 SDP图像转化

实验采集到的4种状态下的振动数据时域波形图,如图7所示。

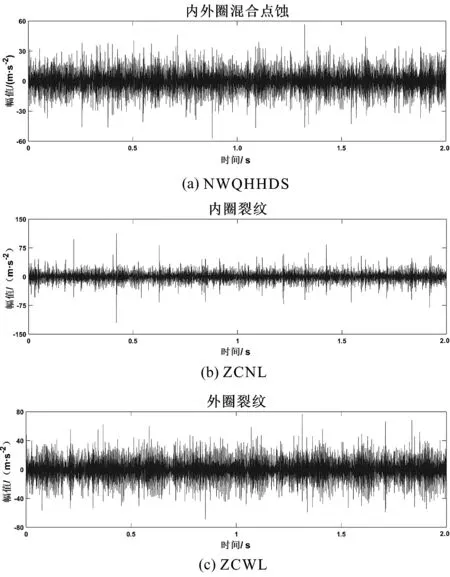
随后,笔者对故障数据进行SDP图像转化,每种故障数据会产生对应的SDP图像。

不同故障数据转化的SDP图像如图8所示。

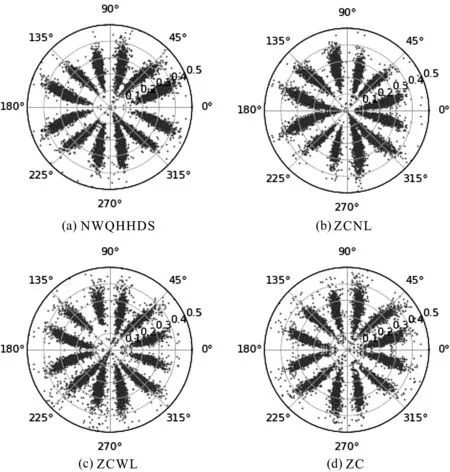
图8 4种故障数据样本的SDP图像

由图8可知:4种类型的故障转化后的SDP图像存在微小差异,不同故障对应的SDP图像主要在图形的曲率、厚度、形状、集中区域上有所不同。

由于SDP图像可以表示出不同轴承故障的信号特征,这可以为之后采用神经网络提取故障特征,以及实现故障的分类提供基础。

2.4 DG-ResNet模型参数选择

由于本研究提出的DG-ResNet模型是深层神经网络模型,为了保证该模型的参数最优,还需要做对照实验,以便找出其最合适的膨胀率和分组卷积个数,适应于相应的轴承故障诊断。

此处笔者选取数据集C作为实验数据集,验证集随机选取50%样本(剩下的50%样本作为测试集)。

本次实验采用NVIDA RTX 5000显卡,8 GB内存,运行环境为64位Windows操作系统下搭建的PyTorch深度学习框架,输出为模型的准确率曲线。

此处笔者设置每次迭代次数为50,每种结构重复5次,取5次结果的平均值作为最后的准确率值。

通过大量的实验,笔者得到了不同BATCH_SIZE、膨胀率和组卷积个数的准确率结果,如图9所示。

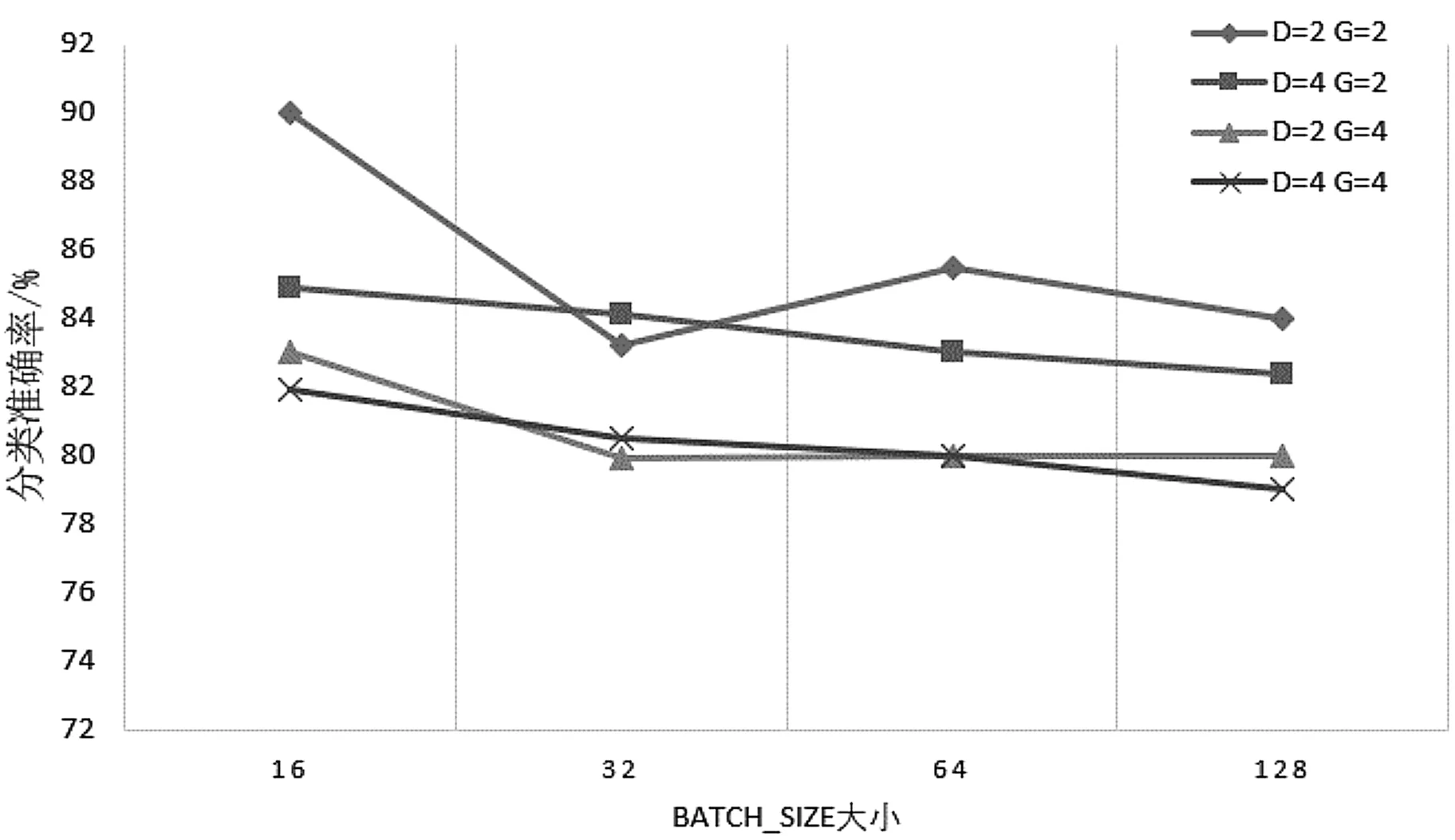
图9 不同BATCH_SIZE、膨胀率和组卷积个数的准确率

由图9可知:在本实验中,当batch_size=16,膨胀率D=2,分组卷积个数G=2时,DG-ResNet模型准确率最高;其次,当batch_size=64,膨胀率D=2,组卷积个数G=2的网络模型准确率较好;膨胀系数为4时的网络模型准确率较差。

本研究选用膨胀率D=2,组卷积个数G=2的网络结构作为膨胀-组卷积残差块。残差块的结构如图10所示。

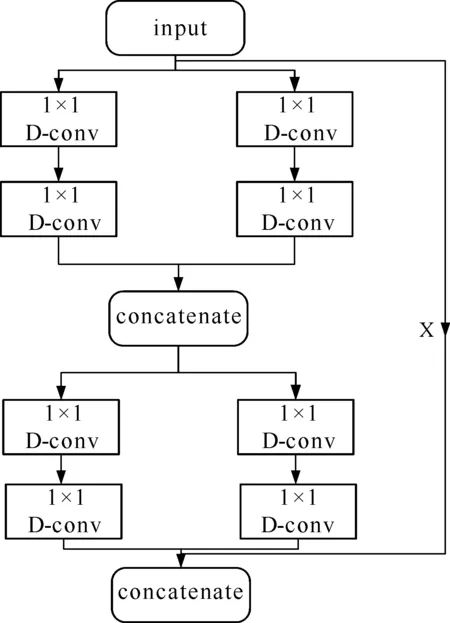
图10 膨胀-组卷积残差块

2.5 结果分析

确定了DG-ResNet结构后,笔者使用采集到的数据集进行了训练和验证。当迭代次数达100次时,数据趋于平稳,此时其故障诊断的准确率达为93%。

测试集的准确率如图11所示。

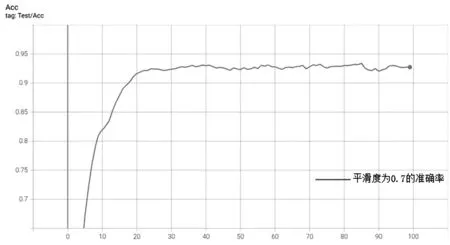
图11 DG-ResNet验证集准确率

图11结果表明:

(1)笔者所提出的故障诊断方法是有效的;(2)使用SDP算法将一维数据转化成二维图像的方法,对故障原始数据的损失小,可以充分地表达轴承原始数据的特征。

3 诊断准确率对比

为了比较所提算法与其他经典算法对故障诊断的效果,本研究使用LeNet、AlexNet和ResNet故障诊断模型与所提算法进行了比较。

在操作时,笔者对各类对比算法同样使用SDP方法,将一维数据转化成图像,然后输出到各自的故障诊断模型中。同时,为了减少其他因素对于对比实验的干扰,笔者针对每种模型都重复操作5次,每次的epoch为100,取平均值作为最后准确率;

所用时间以ResNet作为基准,时间比大于1,则网络所用时间比ResNet所用时间长;反之,则短。

最终,得到的各种诊断方法及其准确率的结果如表2所示。

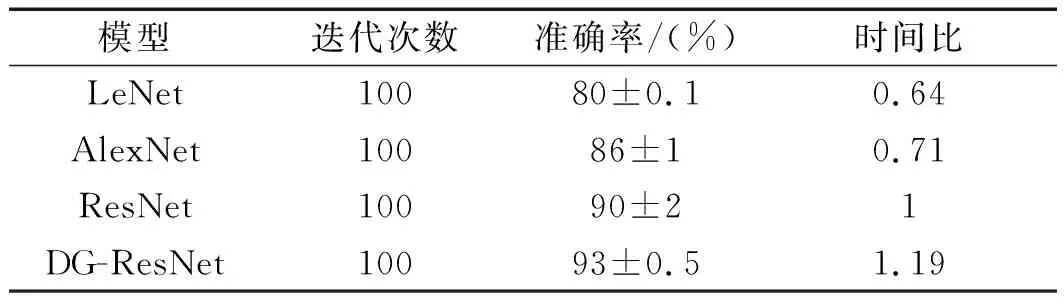
表2 诊断方法及准确率

由表2可知:

(1)提出的DG-ResNet算法对于故障轴承的准确率达到93%,高于LeNet和AlexNet故障诊断算法;(2)其他3种算法的耗时比DG-ResNet算法所用时间短;(3)虽然ResNet诊断准确率和DG-ResNet算法差距不大,但是其波动性大,稳定性不如DG-ResNet算法。

4 结束语

本研究提出了基于SDP和DG-ResNet的轴承故障诊断方法。首先,将轴承振动信号通过SDP方法转化为图像;然后,将图像作为DG-ResNet神经网络模型的输入,对图像进行了轴承故障特征的提取和分类,实现了对轴承故障的高精度、智能化分类;最后,将该方法和多种经典卷积神经网络算法,进行了故障诊断准确率的对比。

实验及研究结果表明:

(1)在故障诊断的准确率上,DG-ResNet网络平均准确率达到93%,相比ResNet网络的平均准确率90%、AlexNet网络的平均准确率85%和LeNet网络平均准确率80%要更高,证明了所提方法的准确性;

(2)在故障诊断的时间上,所提方法的耗时比其他网络用时长;

(3)不同数据集网络的最佳参数不一样,针对每种数据集,应迭代多次取最优参数来进行故障分类。

在不损失数据的前提下,笔者提出的SDP算法能够直观地显示出了原始故障特征,证明了所提方法的有效性。

在后续的实验研究中,笔者将采集齿轮和轴承的复合故障数据,通过基于SDP和DG-ResNet故障诊断模型,并结合解耦分类器,以实现对齿轮和轴承复合故障的分类。