基于改进遗传算法的血液保障车辆应急调度优化研究

张泽瑞，段德光，李 昊，陶学强，鹿国伟，陈 恩

（1．军事科学院系统工程研究院卫勤保障技术研究所，天津 300161；2．西宁联勤保障中心药品仪器监督检验站，兰州 730050）

0 引言

21世纪以来我国频繁遭受自然灾害，诸如汶川、玉树地震和舟曲泥石流等灾害事件给人民群众的生命安全造成了巨大损失，特别是汶川地震，累计死亡69000余人，受伤374000余人[1-2]。应急血液保障是灾害医学救援工作中非常重要的环节[3]，充足且快速的血液供给是挽救灾区伤员生命、提高伤员救治率的重要保证，军队血站及其血液保障车辆在灾后应急血液保障中发挥了重要作用，得到了实战检验[4-6]。

车辆应急调度属于典型的车辆路径问题（vehicle routing problem，VRP），基于其 NP-hard性质，启发式智能算法相较于精确算法更为适用，而遗传算法具有智能性、并行性、良好的鲁棒性等特点[7-8]，被广泛运用于VRP求解。传统遗传算法融合改进策略是提升算法求解效率的主要方式，宋英华等[9]设计了一种加权遗传算法求解以配送时间惩罚成本和驾驶员心理成本最小化的双目标车辆调度模型；Abbasi等[10]提出并行化遗传算法用于加快智能交通系统中复杂VRP的求解。遗传算子的选择是影响遗传算法性能的重要因素，Chaiy等[11]提出一种全新的多点交叉算子求解旅行商问题；Wang等[12]简化编解码方式，采用路径复制交叉算子和基于卫星选择的变异算子用于遗传算法的改进。多种类智能算法结合是近年来算法改进的热点方向，辜勇等[13]将蚁群算法与遗传算法结合，使算法收敛速度得到了提高，解的质量得到了优化；Ariyani等[14]融合遗传算法的全局搜索优势和模拟退火算法的局部搜索优势用于提升算法的搜索效率。以上算法对于VRP求解均展现出较好的性能。

目前，国内外有关血液保障车辆调度与算法的研究仍然较少，且主要集中于平时保障，应急保障涉及较少[15-17]。本研究在灾害医学救援应急血液保障的背景下，考虑血液运输的特殊性和灾后道路路况的复杂性，构建血液保障车辆应急调度模型，设计并改进经典遗传算法，最后进行算例求解与分析，为应急血液保障提供数据支撑与理论参考。

1 问题描述与建模

1.1 问题描述

本文研究的血液保障车辆（以下简称“运血车”）应急调度优化问题描述如下：军队血站（以下简称“血站”）和医疗救治点构成无向图 G=（O，I，D），O 表示血站，I表示医疗救治点，D为边集，运血车配属在血站，按照任务要求完成对多个医疗救治点的血液最优配送，如图1所示。

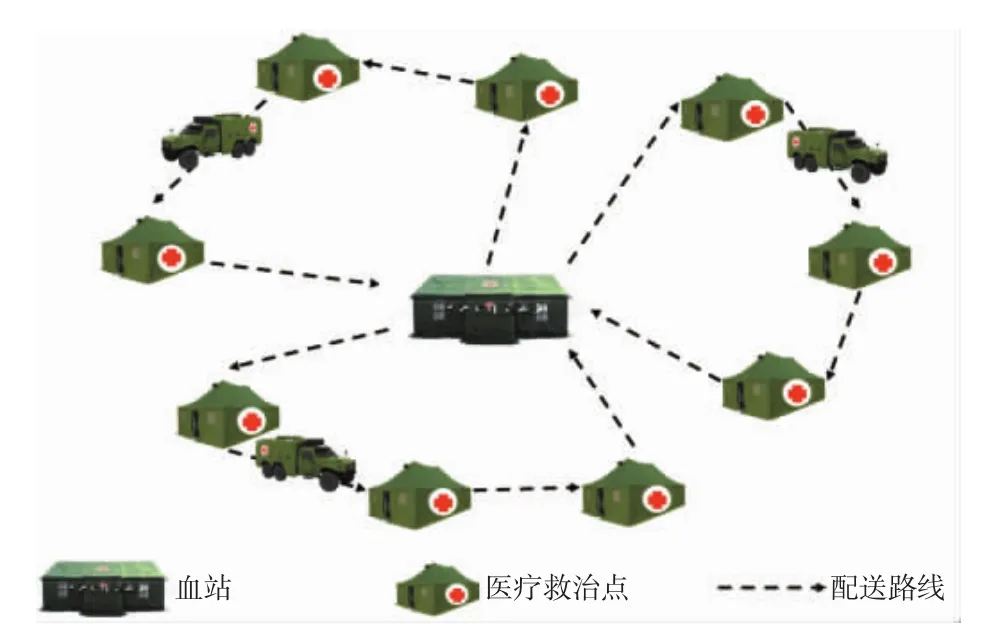
图1 运血车应急调度优化示意图

1.2 模型假设

运血车实际调度的过程复杂，涉及因素众多，需进行一定的抽象和简化。本文主要研究由单一血站出发，同车种、有容量和时间窗约束的车辆调度问题，具体假设如下：

（1）运往各医疗救治点的血液全部在保质期内，不存在过期情况；（2）运送的血液不考虑血型，默认全部为统一血型；（3）不同血液类型（全血、悬浮红细胞、冰冻血浆）均采用统一单位U表示；（4）血液运送采用同种型号运血车，且具有相同的容量限制，始终保持匀速行驶；（5）每一辆运血车均从血站出发，完成运送任务后返回出发点；（6）各医疗救治点的血液需求只能由同一辆运血车满足，且每条巡回路径上只有1辆运血车。

1.3 模型构建

地震、洪涝等自然灾害发生后，伤病员大量产生，血液需求急剧增多，故模型只考虑时间成本，不考虑经济成本。灾害发生地多位于山区，路况差异大[18]，受损概率高，直接影响了血液运输时间，因此考虑灾后道路路况对配送时间的影响和多种类血液需求的特殊性，设置单边硬时间窗和运血车双血库容量限制等约束条件，构建以总配送时间最小化为目标的运血车调度模型，使模型更加贴近现实情况。模型符号说明详见表1。

表1 模型符号说明

模型构建如式（1）～（11）所示：

模型中：式（1）为目标函数，表示总配送时间最短；式（2）表示全血和悬浮红细胞配送总数不超过运血车冷藏血库的容量限制；式（3）表示冰冻血浆配送总数不超过运血车冷冻血库的容量限制；式（4）表示每一个医疗救治点只能由一辆运血车提供服务；式（5）表示派出的运血车数量不超过拥有数；式（6）表示运血车行驶时间；式（7）表示时间窗约束，运血车需要在规定时间窗内将血液送达；式（8）表示运血车到达医疗救治点后的服务时间；式（9）表示运血车到达各医疗救治点时间；式（10）、（11）为决策变量。

2 算法设计

本文在经典遗传算法的基础上引入高效的染色体编码方式，选用指数排序选择算子、顺序交叉算子和倒位变异算子设计改进遗传算法，提高运血车最优配送方案求解效率。

2.1 编码及种群初始化

本文采用整数编码的方式，染色体长度为n+m，整数I1～In表示医疗救治点编码，整数K1～Km表示运血车配送点位数量编码，染色体编码图如图2所示。该种编码方式将整条染色体分为m段，形成m个子回路，每个子回路代表一辆运血车的配送路径。该种编码方式简便且易于理解，能够快速生成大规模染色体群体，且染色体基因段种类丰富。为提升计算效率与收敛效果，缩短不可行解在计算过程中浪费的时间，在初始化种群的过程中加入时间窗和载质量约束筛选因子，将不符合约束的染色体直接去除，直至生成满足种群数量的染色体。

图2 染色体编码图

2.2 适应度评价

适应度是指种群中的个体接近最优解的程度，适应度越大，表示解的性能越好。本文构建的模型目标函数是最小化运血车完成所有配送任务所用的时间，因此以目标函数作为适应度函数，即

2.3 选择操作

本文采用指数排序选择方式增加优质染色体被选择的概率。种群需按照适应度值进行降序排序，排序后个体被选择的概率P（i）为

式中，i、j代表个体的排序；N代表种群数量；c代表底数，c∈[0，1）。c越小最优个体被选择的概率就越大，若c=0，则设置最优个体被选择的概率为1，而其他所有个体被选择的概率为0；c越趋近于1，所有个体越接近等概率选择。

2.4 交叉操作

交叉算子是模仿生物进化中同源染色体交配重组的过程，是种群产生新个体的关键，本文采取文献[19]对比中性能最好的顺序交叉算子，即在父代1中随机选择2个交叉点，找到父代2中截取交叉基因段基因，使子代1与子代2分别保持截取基因段且对应截取基因位置不变，其余按照父代顺序填入，如图3所示。该交叉算子能够在一定程度上实现优良个体的保存，增加种群的多样性，同时避免冲突检测，提高运行效率。

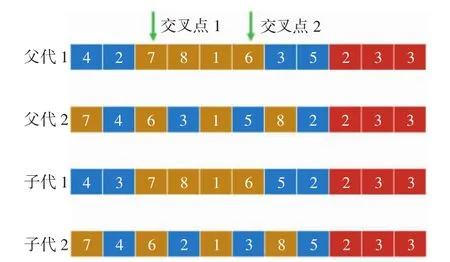
图3 交叉操作示意图

2.5 变异操作

变异是模仿自然界中染色体发生基因突变的现象，是辅助交叉操作，能够恢复因交叉操作而消失的基因。染色体编码中有部分基因段属于最优解基因段，传统基因位突变方式极易造成优质基因段被破坏，故本文采用倒位变异算子[20]，即在个体上随机选择2个变异点，将变异区域的基因序列逆序排列后得到新个体，运血车配送点位数量编码不参与变异操作。倒位变异算子在较好地避免优质基因段被破坏的同时，增加了种群多样性，降低了早熟率。变异操作如图4所示。

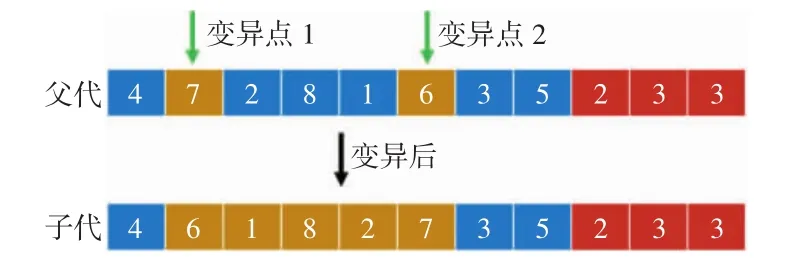
图4 变异操作示意图

2.6 运算步骤

步骤一：设置算法控制参数（种群大小Sizepop、指数排序选择参数c、交叉概率Pc、变异概率Pm、最大迭代数Maxgen）。

步骤二：对运血车路径编码，生成Sizepop数量的初始解（染色体），当前迭代次数gen=0。

步骤三：计算种群中所有染色体适应度值Z，记录当前最优个体Rbest。

步骤四：比较上一代最优个体Rbest*的适应度值Zold与当前最优个体Rbest的适应度值Znew的大小，若Znew＜Zold，则 Rbest=Rbest*，否则不更新。

步骤五：若gen＞Maxgen，跳出循环，生成最终种群，程序结束，否则继续。

步骤六：采用指数排序选择算子进行选择操作。

步骤七：采用顺序交叉算子进行交叉操作。

步骤八：采用倒位变异算子进行变异操作。

步骤九：gen=gen+1，并跳转至步骤三。

运算流程如图5所示。

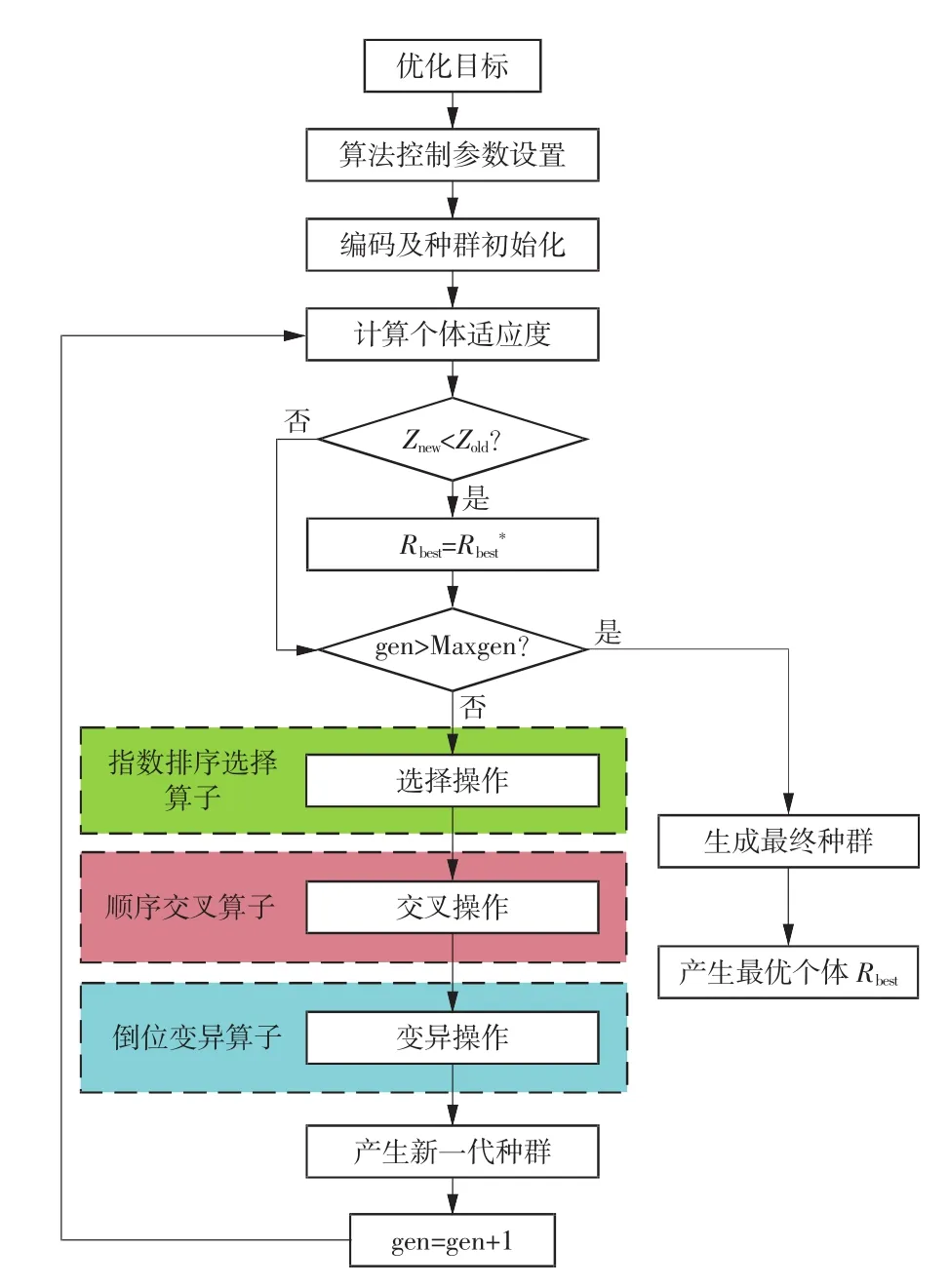
图5 改进遗传算法运算流程图

3 案例求解与分析

3.1 案例描述

某地区发生地震，该保障区域内军队血站迅速完成部署，接受上级指派血液配送任务。该血站共有3辆同种型号的运血车可供调运，运血车具备双血库，其中冷藏血库（4±2）℃可满足全血和悬浮红细胞的储存，冷冻血库（-20±2）℃可满足冰冻血浆的储存，需要在规定时间内完成15个医疗救治点的多种类血液冷链运输。设血站坐标为（102，104），单位为km，随机设置其余点位坐标和时间窗参数（见表2）、路况系数（见表3），各医疗救治点间距离可近似用欧氏距离公式计算，即。参考汶川地震中全血、悬浮红细胞和冰冻血浆消耗的比例[21-22]，生成各点位、各类型血液需求量（见表4）。

表2 各点位坐标和时间窗

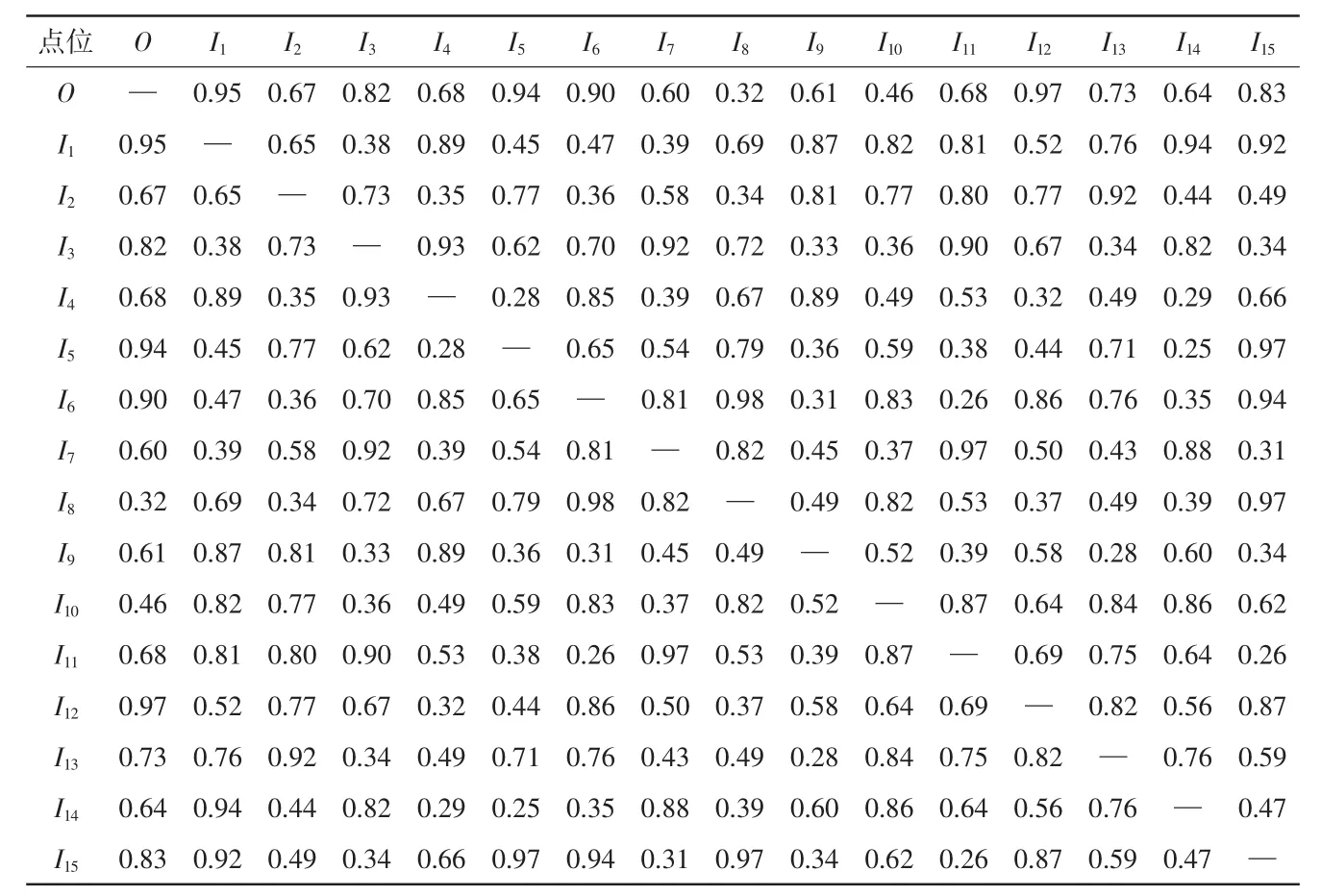
表3 各点位间路况系数

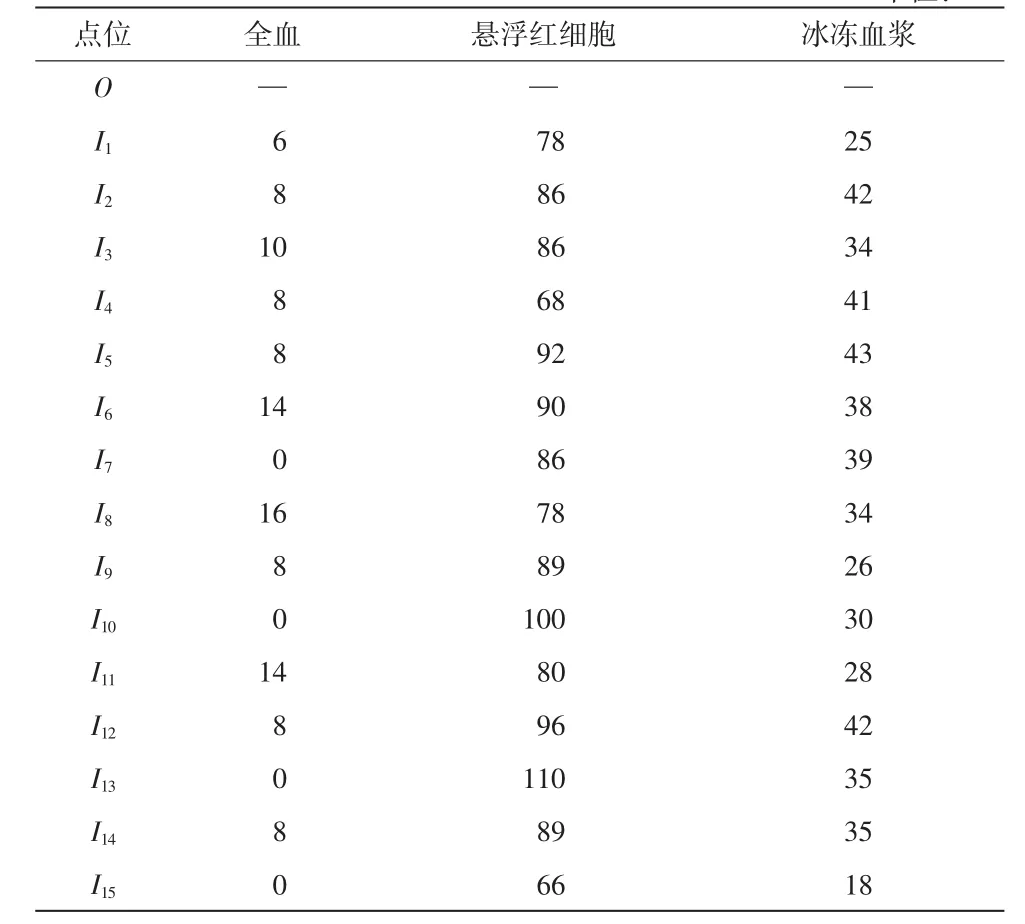
表4 各点位、各类型血液需求量 单位：U

3.2 案例求解

（1）运行环境与参数设置。

采用MATLAB编程，软件在 CPU为 Intel（R）Core（TM）i5-9400 ＠ 2．90 GHz、内存 16 GiB、操作系统为Windows 10的环境下运行。运血车参数设置：冷藏血库载容量L1=500 U，冷冻血库载容量L2=250 U，平均行驶速度v=50 km/h，医疗救治点单位时间内接收血液数量μ=200 U/h。

（2）算法参数敏感性分析。

设置不同种群大小Sizepop、指数排序选择参数c、交叉概率Pc、变异概率Pm和最大迭代数Maxgen，对不同参数组合做算法参数敏感性分析（见表5），对比平均最优适应度值、最优解次数和平均运行时间可知，一方面，增加Sizepop和Maxgen会丰富染色体多样性，有利于最优解的寻找，但影响本算法的运行效率，原因主要在于种群编码和迭代次数，Sizepop越大，Maxgen越大，算法求解速度越慢；另一方面，c、Pc、Pm对求解效率的影响是非线性的，在一定范围内具备较好的性能，故综合考虑本文算法参数设置选择组合1。不同参数组合下的算法运行结果图如图6所示。

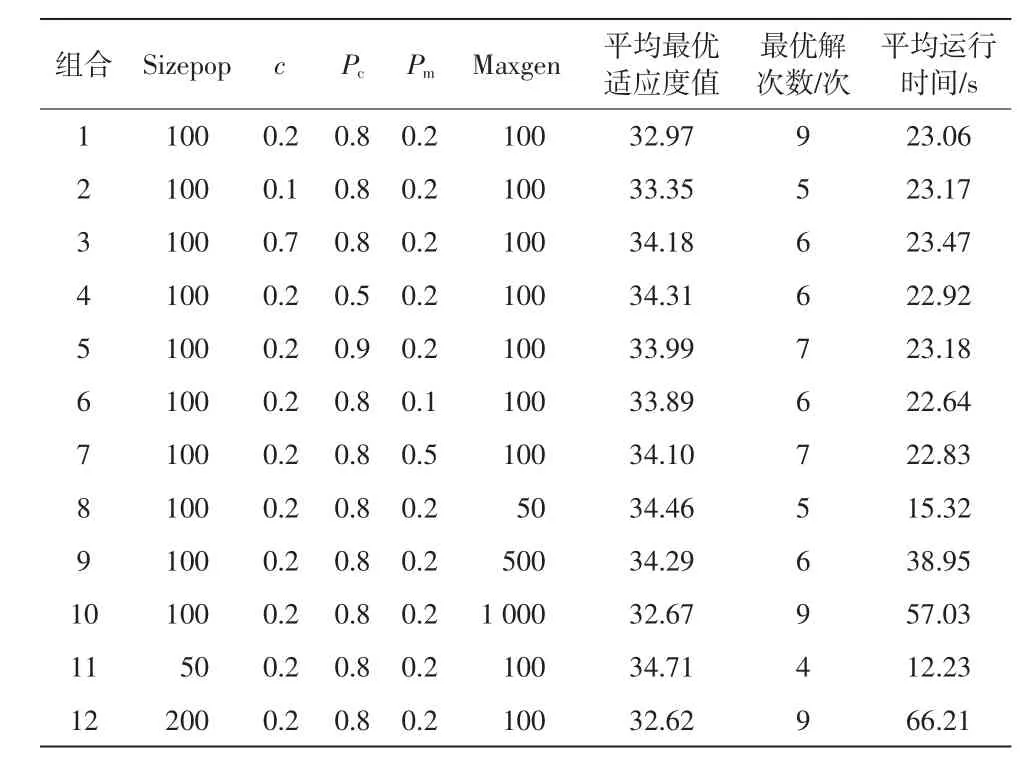
表5 不同参数组合下的算法运行结果

图6 不同参数组合下的算法运行结果图

3.3 案例分析

最优配送路径数据见表6，最优配送路径如图7所示，结果表明，运血车有能力在规定时间内完成血液配送任务，运血车1配送路径耗时为 10．13h，运血车 2 为 10．98 h，运血车3为11．35 h，均未超出时间窗限制；运血车1、运血车2、运血车3冷藏血库满载率分别为86．00%、97．00%、97．40%，冷冻血库满载率分别为 61．20%、69．20%、73．60%，整体血库满载率分别为77．73%、87．73%、89．74%，均未超过载容量限制，因此验证了该算法对于运血车调度问题求解的有效性。

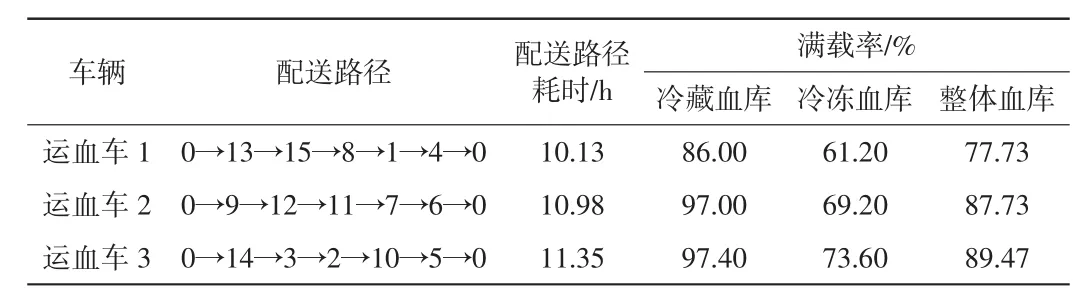
表6 最优配送路径数据

图7 最优配送路径图

分别用经典遗传算法[23]（记为算法1）、文献[24]的遗传算法（记为算法2）与本文的改进遗传算法对比计算，迭代过程中平均最优适应度值变化如图8所示。由图8可知，本文设计的改进遗传算法在迭代22代后保持平稳，即搜索到了最优解32．46，算法1在第87代时开始趋于平稳，算法2在第74代以前陷入了局部最优解，直到第75代才搜索到全局最优解，故本文算法相较于算法1和算法2收敛速度更快，具备更好的运算效率和全局搜索能力。

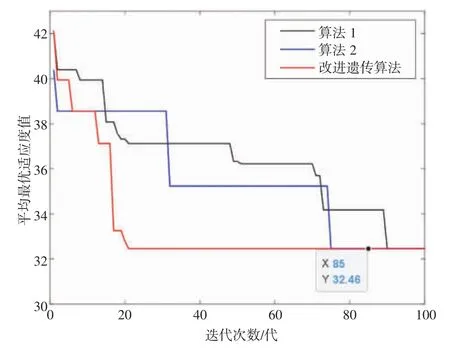
图8 3种遗传算法运行对比图

分别运行3种算法各20次，记录每次搜索到的平均最优适应度值，对3组平均最优适应度值数组做显著性分析（如图9所示），各组进行多重比较后得出：改进遗传算法的平均最优适应度值（32．68）最小，与算法1的平均最优适应度值（35．24）具有极显著差异（P＜0．01），与算法 2的平均最优适应度值（34．63）具有显著差异（P＜0．05），故改进遗传算法较算法1、算法2具备更好的求解性能。

图9 3种遗传算法显著性差异分析图

4 结语

本文基于军队血站在灾害医学救援中的职能任务与特点，考虑灾后道路路况、多种类血液需求、时间窗和运血车载容限制等条件，构建以总配送时间最小化为目标的血液保障车辆应急调度模型，并在基本遗传算法的基础上引入高效的染色体编码方式，选用了顺序交叉算子、指数排序选择算子和倒位变异算子，实现了运血车最优调度方案的高效求解，对大规模灾害救援初期运力受限情况下的血液资源调度问题具有较强的借鉴意义。

但应急血液资源调度在国内外仍属于新兴研究领域，实际调运过程中需要考虑的因素很多，如血液的储存周期、运输损耗、不同血型血液需求等，均为研究提供了新的思路与方向。下一步将加强模型构建的有效性与智能优化算法创新，为血液资源与保障装备的优化配置提供更有效的辅助决策支持。