一维光子晶体中的几率密度和拓扑相
任明丽, 韩 梦, 刘晓静, 吴向尧
(吉林师范大学 物理学院, 吉林 四平 136000)
随着量子Hall效应(QHE)在凝聚态物理中的深入研究, 一类具有非平庸特性的新型材料----拓扑绝缘体已引起人们广泛关注[1-7], 如用拓扑不变量[5]解释量子Hall效应[6-7]. 近年来, 随着人工超材料[8-10]的发展, 凝聚态中的拓扑绝缘体为类似光学[11-12]和声学[13]的拓扑绝缘体发展奠定了基础. 拓扑绝缘体的概念已扩展到光子学[14]中, 一维光子晶体(PCs)的拓扑特征是Zak相[15], 计算结果表明, Zak相与PCs表面阻抗是相关的[16], 并且一个孤立带的Zak相位与具有完美透射特征的奇点有关[17-18]. 在二维空间中, 具有Faraday效应的PCs与手性边缘模式的量子Hall效应系统相似[19-20], 在传统的蜂窝晶格中也可实现自旋Hall效应和谷Hall效应[21-22]. 文献[23]用量子理论方法计算了一维光子晶体的量子色散关系、量子透射率和反射率. 本文在此基础上计算一维光子晶体中光子的几率密度和几率流密度, 并用该量子理论方法研究带的Zak相.
1 一维光子晶体中光子的几率密度和几率流密度
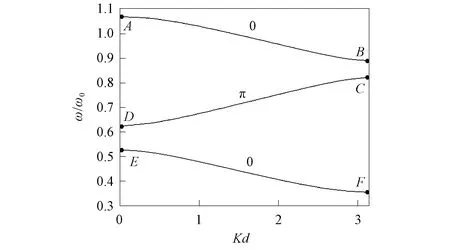
当0 (1) 由方程(1)和(2)可计算一维光子晶体中光子的几率密度, 第一个周期介质层A的几率密度为 当a (4) 第一个周期介质层B的几率密度为 在第N个周期介质层A的光子波函数为 第N个周期介质层A的几率密度为 在第N个周期介质层B的光子波函数为 第N个周期介质层B的几率密度为 其中Na+(N-1)b 由文献[19]中的方程(9)可得光子在各介质层的几率流密度. 当0 当a 在第N个周期介质层A的几率流密度为 其中(N-1)(a+b) 在第N个周期介质层B的几率流密度为 其中Na+(N-1)b (17) 和 (18) 其中 p=1+C1/C2,q=1-C1/C2,g1=(1+C2/C3)eiK0C2·a,g2=(1-C2/C3)e-iK0C2·a,g3=(1-C2/C3)×eiK0C2·a,g4=(1+C2/C3)e-iK0C2·a,h1=(1+C3/C2)eiK0C3·b,h2=(1-C3/C2)e-iK0C3·b,h3=(1-C3/C2)eiK0C3·b,h4=(1+C3/C2)e-iK0C3·b. 当介质A和B的折射率分别为na=2.68和nb=1.68, 厚度分别为a=200 nm和b=300 nm, 周期数N=10, 中心频率ω0=171 THz时, 计算结构为(AB)N的一维光子晶体的量子透射率、几率密度和几率流密度. 在数值计算中, 比较量子透射率和经典透射率的结果, 并进一步研究一维光子晶体不同参数对几率密度、几率流密度、带隙结构和Zak相的影响. 由文献[19]中的方程(88)可得一维光子晶体的量子透射率, 结果如图1所示, 其中图1(A)为经典透射率, 图1(B)为量子透射率. 由图1可见, 量子透射率与经典透射率的结果相同. 入射角θ对几率密度和几率流密度的影响分别如图2和图3所示. 由图2和图3可见: 几率密度和几率流密度均随光在光子晶体中的传播距离x呈近似周期性变化; 随着入射角θ的减小, 几率密度和几率流密度的波幅增大. 周期数N对概率密度的影响如图4所示. 由图4可见, 几率密度的波幅随周期数N的增加而增大. 一维光子晶体(AB)10对不同ω的几率密度如图5所示. 由图5(A)可见, 当取透射率T=100%对应的入射光子频率时, 几率密度的波幅值最大; 由图5(B)可见, 当取入射光子频率对应的透射率T=80%时, 几率密度波幅值减小; 由图5(C)可见, 当取入射光子频率对应的透射率T=0时, 光子的禁带频率和几率密度的幅值迅速衰减为零, 表明光子晶体禁带中的光子存在量子隧道效应. 图1 一维光子晶体(AB)10的透射率Fig.1 Transmissivity of one-dimensional photonic crystals (AB)10 图2 一维光子晶体(AB)10对不同入射角θ的几率密度Fig.2 Probability density of one-dimensional photonic crystals (AB)10 for different incident angle θ 图3 一维光子晶体(AB)10对不同入射角θ的几率流密度Fig.3 Probability current density of one-dimensional photonic crystals (AB)10 for different incident angle θ 图4 一维光子晶体(AB)10对不同周期数N的几率密度Fig.4 Probability density of one-dimensional photonic crystals (AB)10 for different periodic number N 由文献[22]可知光子的量子几率密度分布, 当Kd=0和Kd=π时, 若同一条带上ρn(x=0)和(x=π)均为0或均不为0时, 则这条带的Zak相为0; 否则Zak相为π. 当几率密度ρ≤10-3时, 可将其视为零. 图5 一维光子晶体(AB)10对不同ω的几率密度Fig.5 Probability density of one-dimensional photonic crystals (AB)10 for different ω 图6 一维光子晶体的色散关系Fig.6 Dispersion relation of one-dimensional photonic crystals 一维光子晶体的色散关系如图6所示, 其中介质B的折射率为nb=1.12, 点A,B,C,D,E,F为带边态, 其量子几率密度分布分别如图7(A)~(F)所示. 根据光子在光子晶体中的量子几率密度分布可确定带Zak相位. 对于AB带,ρA(x=0)=0.214 1≠0,ρB(x=0)=0.42≠0, 则AB带的Zak相位为0; 对于CD带,ρC(x=0)=0.003 618≈0和ρD(x=0)=0.017 68≠0, 则CD带的Zak相为π; 对于EF带,ρE(x=0)=0.003 419≈0和ρF(x=0)=0.000 442 4≈0, 则EF带的Zak相位为0. 图7 量子几率密度分布Fig.7 Distribution of quantum probability density 综上, 本文用光子量子理论给出了一维光子晶体中光子的几率密度、几率流密度和拓扑相, 通过MATLAB软件进行计算画图. 结果表明: 当入射角θ和周期数N改变时, 几率密度和几率流密度近似为周期变化, 其振幅随入射角θ和周期数N的增加而增大; 当入射光子的频率与透射率T=100%相对应时, 几率密度振幅最大, 当入射光子的频率与透射率T=0相对应时, 几率密度不为零, 但几率密度的振幅迅速衰减到零, 即光子晶体中存在光子的量子隧道效应. 此外, 用量子方法给出了带的Zak相, 该量子理论方法可进一步研究光的量子Hall效应, 为光子晶体器件的设计提供数据信息.

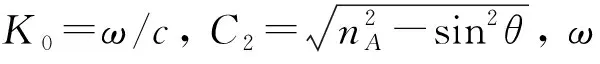


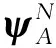
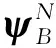

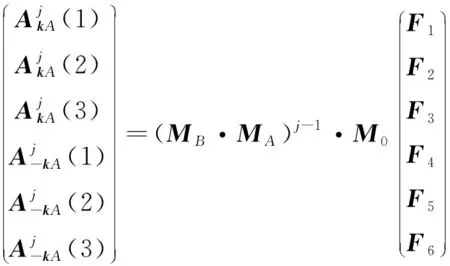

2 数值结果