基于函数尺度因子的有理分形插值及其应用*
宋 刚, 杨晓梅, 姜 群, 包芳勋, 张云峰
(1. 山东大学 数学学院, 济南 250100; 2. 山东财经大学 计算机科学与技术学院, 济南 250014)
曲线造型技术在工业设计、航天技术、数字城市、媒体设计、医学可视化等领域应用广泛. 但传统的曲线插值方法, 如多项式插值、有理插值、样条插值等, 通常都是生成光滑或分段光滑的曲线, 不适合从海岸线、云层和裂缝、岩石、雪花等实际现象中逼近或拟合高度不规则的数据. 分形插值的概念由Barnsley[1]首次通过一个迭代函数系统(IFS)提出, 可拟合和逼近复杂真实现象中的不规则数据. 目前对分形曲线的研究已有许多, 如: 文献[2-5]讨论了分形插值函数(FIFs)的构造; 文献[6-9]研究了FIFs的一些性质, 包括误差、中心变差、曲线的光滑性、稳定性和分形维数等; 文献[10-12]进一步将分形插值推广到Hermite分形插值和样条分形插值. 近年来, 传统的多项式分形插值被拓展到有理的情形, 将形状参数嵌入到IFS中[13-15].
上述研究所给出的单变量FIFs大多是由具有常数尺度因子的IFS生成, 因此所构造的曲线有明显的自相似特性, 这种分形插值方法很难精确拟合或逼近自相似性较弱的不规则数据. 因此, 有必要研究具有可变尺度因子的FIFs, 但对该问题的研究目前报道较少. 文献[16]研究了具有函数尺度因子的FIFs的一些分形特性, 包括光滑性、稳定性和敏感性; 文献[17]给出了具有可变参数的FIFs的显式表示; 文献[18]引入了一类具有可变参数的IFSs, 使得FIFs的生成灵活性更大; 文献[19]使用具有函数尺度因子的有理IFS构造了分形插值曲线, 估计了其计盒维数. 上述研究都是基于多项式函数的具有函数尺度因子的IFSs.
研究表明, 有理函数比多项式函数能更有效、更灵活地描述复杂的实际现象. 本文首先利用传统的带有形状参数的有理样条插值方法, 构造一类具有函数尺度因子的有理分形插值曲线; 其次研究有理FIFs的一些性质, 并估计有理分形曲线计盒维数的上下界; 最后通过数值算例验证所给模型的有效性.
1 有理分形插值模型
1.1 有理分形插值模型的构建
1.1.1 分形插值函数
设(xi,yi)为给定的一组数据点, 满足:
{(xi,yi)∈I×:i∈Λ*={0,1,…,N}},
其中I=[a,b]=[x0,xN]⊆. 设Ii=[xi,xi+1], 其中i∈Λ={0,1,…,N-1}. 令压缩映射Li:I→Ii满足:
其中0≤l<1. 令连续映射F=I×,Fi:F→满足:

(1)
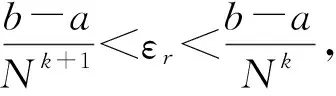
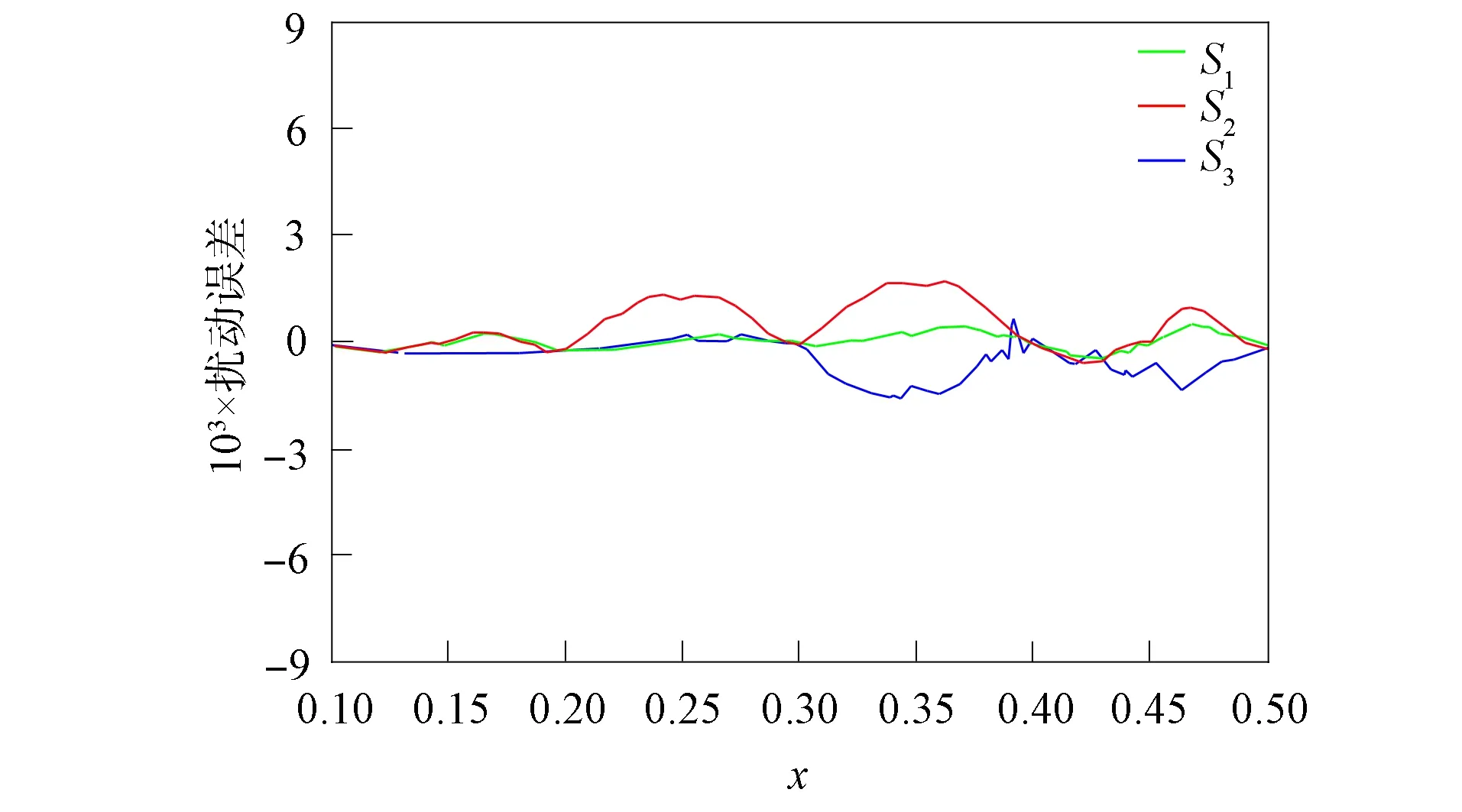
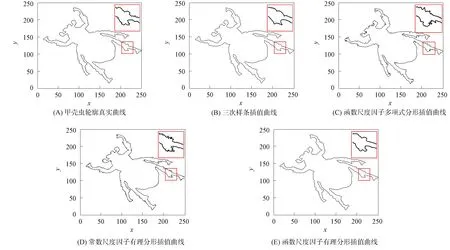
其中-1 定义函数ωi:F→F为 ωi(x,y)=(Li(x),Fi(x,y)),i∈Λ. 迭代函数系统(IFS){F;ωi:i∈Λ}生成唯一的吸引子, 它是连续函数f:I→的图像, 称函数f为一个FIF, 满足f(xi)=yi(i∈Λ*), 并且 目前常用的FIFs基于以下IFS: (2) 其中 参数si称为尺度因子, 函数qi:I→(i∈Λ)是满足条件(1)的连续函数. Barnsley[1]证明了当qi(x)=Pi∘Li(x)-siBi(x)时, 对应的FIFφ满足φ(xi)=Pi(xi)(i∈Λ*), 这里Pi(x)和Bi(x)是连续函数, 且Bi(x)满足Bi(x0)=φ(x0),Bi(xN)=φ(xN). 下面利用数据集{(xi,yi):i=1,2,3,4,5}解释迭代过程: 首先, 对于每个i(i=1,2,3,4), 压缩映射Li(x)将区间[x1,x5]映射到子区间[xi,xi+1], 从而[xi,xi+1]获得5个点, 如图1(A)所示. 其次, 每个子区间提供5个插值点, 通过迭代方案(2)可以获得对应子区间插值曲线上的5个插值点, 以区间[x2,x3]为例, 如图1(B)所示. 因此, 第一次迭代后得到区间[x1,x5]上17个点. 相同情形也会发生在更多的迭代中. 图1 迭代系统Fig.1 Iterative system 1.1.2 有理分形插值曲线的构造 设{(xi,fi,di),i∈Λ*}为给定的一组数据集, 其中x0 (3) 其中 基于式(3)定义的有理函数插值性质, 有 从而 Vi=αifi+hidi,Wi=βifi+1-hidi+1. 类似式(3), 构造扰动基函数Bi(x)为 (4) 其中 式(4)满足 于是得 V1i=αif1+hNd1,W1i=βifN-hNdN. 下面考虑具有函数尺度因子的IFS: (5) 其中si(x)是I上的Lipschitz函数, 且 ‖si‖∞=sup{|si(x)|:x∈I}<1. 可证明具有函数尺度因子的FIFs为 φ(Li(x))=si(x)φ(x)+Pi(Li(x))-si(x)Bi(x),x∈I,i∈Λ. (6) 将式(6)改写为 (7) 其中 注1如果对任意的i∈Λ, 尺度因子函数si(x)恒为0, 则RFIFs退化为经典的有理插值函数Pi(x). 进一步, 如果对任意i∈Λ, 尺度因子函数si(x)恒为0, 且αi=βi=3, 则有理RFIFs与C1Hermite插值一致. 表明在RFIFs中, 尺度因子的存在允许获得不同于经典插值的各种形式. 插值函数(3),(4)由函数值和导数值表示, 为简化, 可重写为 Pi(Li(x))=ω1(θ,·i)fi+ω2(θ,·i)fi+1+ω3(θ,·i)hidi+ω4(θ,·i)hidi+1, Bi(x)=ω1(θ,·i)f1+ω2(θ,·i)fN+ω3(θ,·i)hNd1+ω4(θ,·i)hNdN, 其中 {ωk(θ,·i):k=1,2,3,4}为Pi(Li(x))和Bi(x)的基函数, 满足 ω1(θ,·i)+ω2(θ,·i)=1,ω3(θ,·i)-ω4(θ,·i)≤1. 1.2.1 稳定性 稳定性是评价插值函数质量的重要指标, 其衡量插值数据的抗干扰能力. 其中 证明: 根据式(6), 有 进一步, 得 同理, 有 由于上述不等式对于任何i∈Λ都成立, 因此 1.2.2 收敛性 图10为两种电流供电情况下振动加速度频谱。对比正弦波供电,当逆变器供电时,振动幅值整体增加。不同电流供电下振动加速度的最大幅值点均出现在8 500 Hz,9 533 Hz,10 700 Hz,11 400 Hz附近,接近模态分析结果中0阶和8阶固有频率。开关频率10 kHz附近振动加速度增加较大,究其原因是引入逆变器开关频率的谐波电流加剧了高频段的结构共振。 在实际应用中, 通常用误差评价插值模型的精度. 误差越小, 精度越高. 下面考虑RFIFφ(x)逼近原函数的有效性. 定理2设f为生成数据点的原始函数{(xi,fi),i∈Λ*},φ(x)和Pi(x)是由式(7)和经典有理三次插值函数构造的RFIF, 则分别存在常数C和C*, 满足下列条件: 1) 如果f∈C1(I), 则有 2) 如果f∈C2(I), 则有 其中 E(h)=‖f‖∞+hD1,E*(h)=F1+hND2, 证明: 由文献[20]的结果, 可得 (8) 进一步, 根据三角不等式, 有 ‖f-φ‖∞≤‖f-Pi‖∞+‖Pi-φ‖∞. (9) 因此, 只需讨论式(9)右边的第一项. 1) 如果f∈C1(I),x∈Ii, 则根据Peano-Kernel定理[21]得 2) 如果f∈C2(I), 根据文献[22], 类似可得 ‖f-φ‖∞≤C*h2‖f(2)‖∞, (10) 其中 结合式(8),(9)及三角不等式, 可知2)成立. 1.2.3 计盒维数 曲线的分形维数是衡量曲线不规则性的一个指标, 其刻画了曲线的粗糙程度. 本文基于盒子覆盖法研究有理分形曲线的计盒维数. 在分形几何中, 计盒维数也称为盒维数, 是一种计算分形维数的方法. 计盒维数定义如下: 设F为定义在n上的任意非空有界子集,Nδ(F)为利用边长为δ方块覆盖F集合的最小数目, 则F的计盒维数为 由式(7)定义的FIFφ(x)可知, 下列引理成立: 引理1设Rf[I]=sup{|f(x2)-f(x1)|:x1,x2∈I},φ(x)是由式(7)定义的FIF, 则 其中 N2=Lsi(N0+M0)+LPi,M0=max{|φ(x)|:x∈I}, Lsi和LPi分别是函数si(x)和Pi(x)的Lipschitz常数. 下面考虑等距节点的情形, 即对于所有i∈Λ,hi=hi+1, 若令 定理3假设由式(5)定义的IFS吸引子G是连续函数φ(x)的图, 将该函数对给定数据点{(xi,yi):i∈Λ*}进行插值, 插值点不共线, 且hi=hi+1(i∈Λ), 则G的计盒维数dimBG满足下列条件: 证明: 当迭代系统迭代一次后, 在每个区间Ii(i∈Λ)内均可得到(N+1)个新点. 由假设可知, 在每个区间Ii上至少有3个点不共线. 设从三点之一的y轴方向到其余两点的最大垂直距离为hi, 则根据引理1, 每个区间Ii内的最大范围为 定义非负向量H1,K,U1,E如下: 定义 Φ(c)=c1+c2+…+cn,c=(c1,c2,…,cn), 由于G是定义在I上连续函数的图像, 因此用边长为εr(εr<(b-a)/N)的正方形覆盖Ii×∩G的最小正方形数, 大于用边长为hi的正方形覆盖垂直线的最小正方形数, 并且小于覆盖矩形的最小正方形数. 因此, (11) 其中 因此, 有 (13) 因此, 因此, 注3当函数尺度因子si(x)为常数si(对所有的i)时, 则吸引子G的计盒维数满足下列条件: 1) 当λ>1时, 有dimBG=1+logNλ; 2) 当λ≤1时, 有dimBG=1. 由式(7)定义的上述RFIFφ(x)包含原函数的导数值, 本文用算术平均法[23]估计导数值di(i∈Λ*): 其中Δi=(fi+1-fi)/hi,i∈Λ. 下面举例证明所提出的RFIFs的近似有效性, 并说明有理分形曲线在特定函数插值数据扰动下的稳定性. 例1考虑表1所列的插值数据, 该数据是由函数f(x)=sinx(x∈[0.1,0.5]), 通过将其值近似到四位小数生成的. 表2是表1中数据的扰动. 表1 函数f(x)插值数据 表2 表1中数据的扰动数据 图2 表3中不同函数尺度因子下的扰动误差曲线Fig.2 Perturbation error curves with different function scaling factors in table 3 确定形状参数 α1=α2=1,α3=0.002,α4=0.01, β1=β2=0.8,β3=0.004,β4=0.04. 为证明函数尺度因子的有效性, 在插值数据的4个子区间选用不同的函数尺度因子, 列于表3. 图2给出了不同函数尺度因子相应的扰动误差曲线, 表示插值数据拟合曲线与扰动数据拟合曲线之间的误差曲线. 由图2可见, 扰动误差介于-3×10-3~5×10-3间. 结果表明, 本文构造的有理分形插值曲线具有良好的抗干扰能力, 即对插值数据的扰动稳定性很好. 表3 函数尺度因子在数值算例中的应用 此外, 根据定理2选择函数尺度因子, 分别在图3中生成误差曲线f(x)-φ(x), 表示原函数曲线与插值数据拟合曲线之间的误差曲线. 由图3可见, 误差值介于-3×10-3~3×10-3间. 结果表明, 本文所提出的RFIFs对原函数f(x)具有较好的逼近结果. 例2用于曲线粗糙度分析的插值数据列于表4. 不同的函数尺度因子见表3. 表4 用于曲线粗糙度分析的插值数据 对于相同的插值数据和形状参数, 图4为根据不同的函数尺度因子得到的分形插值曲线. 图4验证了函数尺度因子在有理IFS中的关键作用, 有理分形曲线在不同的函数尺度因子作用下具有不同的粗糙度. 图3 表3中不同函数尺度因子下的误差曲线Fig.3 Error curves with different function scaling factors in table 3 图4 表3中不同函数尺度因子下的曲线粗糙度Fig.4 Roughness of curves with different function scaling factors in table 3 下面利用本文提出的有理样条分形插值模型重构Fibonacci螺旋曲线. 图5(A)为原始Fibonacci螺旋曲线; 图5(B)为三次样条插值结果; 图5(C)为函数尺度因子多项式分形插值结果; 图5(D)为常数尺度因子有理分形插值结果, 其中常数尺度因子为0.1; 图5(E)为函数尺度因子有理分形插值结果. 图5 Fibonacci螺旋曲线建模Fig.5 Fibonacci spiral curve modeling 由图5可见, 本文提出的插值模型在Fibonacci螺旋曲线建模中效果较好. 下面给出定量分析数据, 以进一步对逼近效果进行测评. 采用均方根误差(root mean square error, RMSE)作为误差分析指标, 能很好地反映测量的精密度. 计算可知: 三次样条插值、函数尺度因子多项式分形插值、常数尺度因子有理分形插值、函数尺度因子有理分形插值的RMSE分别为0.000 8,0.000 5,0.000 5,0.000 4. 结果表明, 本文提出的函数尺度因子有理分形插值方法能精确拟合规则曲线. 下面利用本文提出的有理样条分形插值模型重建物体的轮廓曲线. 以MPEG-7数据集中的甲壳虫轮廓曲线为例进行实验, 该数据集在计算机视觉领域被广泛应用于形状分析[24]. 图6(A)为原始甲壳虫曲线; 图6(B)为三次样条插值结果, 图6(C)为函数尺度因子多项式分形插值结果; 图6(D)为常数尺度因子有理分形插值结果, 其中常数尺度因子为0.4; 图6(E)为函数尺度因子有理分形插值结果. 为更好地分析实验结果, 用小矩形框显示了局部细节. 图6 物体轮廓曲线建模Fig.6 Object contour curve modeling 由图6可见: 与三次样条插值方法相比, 本文模型能更有效地保留曲线的局部细节信息; 此外, 在函数尺度因子多项式分形插值与常数尺度因子有理分形插值的局部放大图像中, 边缘位置能观察到尖锐的突起. 表明本文模型在曲线边缘保持上表现出色, 能较好地保持原始曲线的局部细节. 计算可知: 三次样条插值、函数尺度因子多项式分形插值、常数尺度因子有理分形插值、函数尺度因子有理分形插值的RMSE分别为0.020 6,0.008 7,0.006 1,0.004 6. 结果表明, 本文提出的函数尺度因子有理分形插值方法对甲壳虫轮廓曲线拟合的RMSE值最小, 表明该方法具有更强的逼近能力. 下面将本文提出的插值模型应用于自然海岸线曲线建模, 该地形数据从国家海洋和大气管理局(NOAA)获取. 图7(A)为原始海岸线曲线; 图7(B)为三次样条插值结果; 图7(C)为函数尺度因子多项式分形插值结果; 图7(D)为常数尺度因子有理分形插值结果, 其中常数尺度因子为0.2; 图7(E)为函数尺度因子有理分形插值结果. 由图7(B)可见, 三次样条插值方法插值结果中曲线明显失真; 由图7(C),(D)可见, 局部放大区域中的边缘位置出现冗余信息. 计算可知: 三次样条插值、函数尺度因子多项式分形插值、常数尺度因子有理分形插值、函数尺度因子有理分形插值的RMSE分别为0.043 4,0.004 3,0.003 1,0.002 6. 结果表明, 本文提出的函数尺度因子有理分形插值方法的拟合效果在RMSE数值指标上优于其他曲线插值方法. 图7 海岸线曲线建模Fig.7 Shoreline curve modeling 实验结果表明, 本文提出的函数尺度因子有理样条分形插值模型优于其他对比方法, 更适用于重建真实数据与不规则数据. 综上可见, 本文构造的有理分形插值不仅具有传统有理样条插值的优点, 而且能有效描述高度不规则的数据. 表明具有函数尺度因子的有理分形曲线比经典有理样条曲线灵活性更高, 在处理实际问题中更有效.


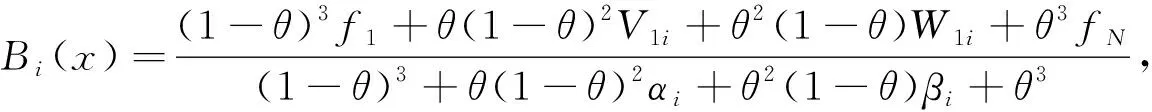
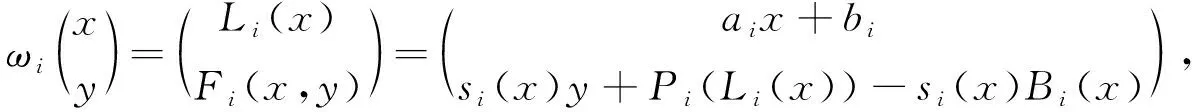

1.2 有理FIFs的性质

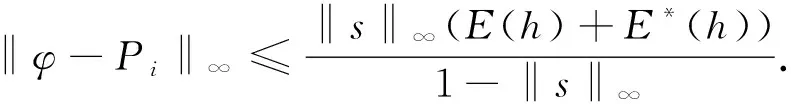




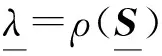

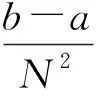

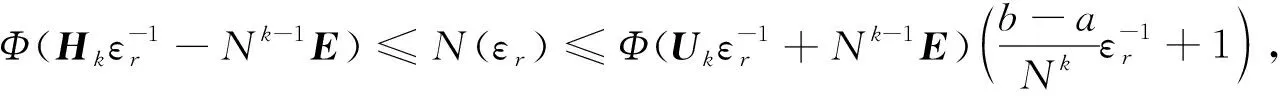
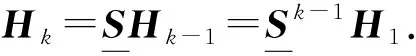
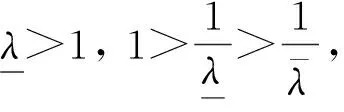



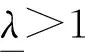
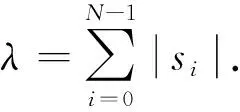
1.3 数值算例






2 实 验
2.1 Fibonacci螺旋曲线建模

2.2 物体轮廓曲线建模
2.3 海岸线曲线建模


