工程机械液压缸内泄漏故障检测分析

黄 克

（德州职业技术学院，山东德州 253034）

0 引言

液压缸是大型机组设备中不可或缺的重要液压执行元件，主要用于将液压能转变为机械能，并做直线往复或摆动运动[1]。液压缸结构简单、工作可靠，用于实现往复运动时无需装设减速装置，且没有传动间隙，运动平稳，因此在各类机组设备的液压系统中得到了广泛应用。但在实际运行期间，液压缸经常出现泄漏故障。为及时检测出故障的类型，需探索行之有效的解决方式。

1 液压缸泄漏原因分析

（1）密封件结构形式与材料因素。如果用于密封的材料质地硬度不足，则在液压缸处于工作状态时，密封件十分容易“挤进”密封间隙。在此过程中，液压缸会出现损伤，逐渐导致液压油渗漏[2]。

（2）密封槽与密封接触表面的质量较差。一般情况下，液压缸密封件安装在尺寸精度相对较低、表面粗糙程度以及形位公差均较低的密封槽内，密封件会受到磨损，进而泄漏液压油。

（3）通常而言，对液压缸密封件的要求为：①尺寸精度必须较高；②形状位置精度必须准确。若上述两项精度要求不达标，则密封件在装配过程中会受到磨损，进而导致内泄漏。

（4）大型机组设备运转过程中会产生热量，导致工作环境长时间处于高温状态，若不能及时降温，则密封件的老化速度将会加快。若缺乏有效的检修维护制度，无法及时发现密封件的老化情况，则密封效果会逐渐降低，最终导致泄漏。

（5）某些液压缸装有缓冲阀，在设备运转期间，阀芯与阀座极易出现磨损情况，同样会导致液压缸内泄漏。

2 液压缸内泄漏故障的检测方式

2.1 数学建模要素分析

在实际工作中，常用的检测工程机械液压缸内泄漏故障的方法主要为经验诊断法，即观察液压系统的工作压力，若相关参数并未达到标准值，且在调节安全阀的过程中，压力参数并未出现明显变化时，便可怀疑液压缸内有可能出现内泄漏故障。但此种方式的直观性较低，当技术人员经验不足时，很可能无法及时发现内泄漏故障，液压缸及邻近机组设备均可能受到影响。本研究设计一种基于数学建模方式的液压缸内泄漏故障的检测方法，主要原理如下：

（1）所选取的液压缸系统为负载传感液压系统，是非对称性液压缸。建立数学模型时，必须具备的参数主要来源于两个方面：一是液压缸本身的结构组成；二是液压缸运行期间产生的参数。具体而言：①液压缸（泵）出口处的压力，以p′表示；②液压泵单位时间的流量，以Q′表示；③液压缸进油管道的上液阻力，以R1表示；④液压缸进油管道的流量，以Q11表示；⑤液压缸回油管道的上液阻力，以R2表示；液压缸回流管道的流量，以Q21表示；⑥液压缸内泄漏的液体阻碍压力，以R 表示；液压缸内泄漏的流量，以Q 表示；⑦流进、流出液压缸的流量，分别以Q12、Q22表示；⑧液压缸进油腔的压力以及出油腔的压力，分别以p1和p2表示；⑨在没有发生内泄漏事故时，对称液压缸输出动力以及出现内泄漏故障时对称液压缸的输出动力分别以F1和F2表示；⑩液压缸活塞的运动速度，以v 表示。

（2）上述基础参数仅仅是构建数学模型的基础参数。除此之外，液压泵运行期间重要参数之间的关系满足公式（1）：

式中，Δpλ 是液压系统运行期间必然产生的“沿程压力损失”；λ 是沿程阻力系数；l 是管道长度；d 是管道直径；ρ 是液压油本身的参数——密度；v 是液压油的流动速度。q=π/4·d2v 是流量公式，将该公式带入式（1），得到：

变换后，其中一个变量——液压油的流动速度v 消失。在剩余的参数中，沿程阻力系数λ、管道长度l、管道直径d、液压油密度均是固定值且均为常数。以此为基础，可定义一个参数R（液压缸内泄漏的液体阻碍压力）。具体的关系为：

根据式（3）的构成参数可知，液阻R 的参数是一个固定值（除λ 等参数之外，π 是定值，故R 值也必然固定）。至此完成检查机械液压缸内渗漏故障的数学模型，以液阻R 替代繁琐的参数表示项之后可以发现，液压系统的沿程压力损失Δpλ=Rq2。式中唯一的变量即为q，而q 实际上即为液压油的流量，在条件满足时可与Q′等参数互相转换（q 可视为Q′等参数的“替代表示值”）。为进一步增强理论计算过程中的便利性，可将液压缸内泄漏过程中的液阻R、R1、R2分别与其产生的油液压力损失（RQ2、R1Q2、R2Q2）相互对应，可使后续计算过程及结果显示的直观程度大幅度提升。

2.2 液压缸的动力特性分析（基于模型阐述）

在液压缸并没有出现泄漏事故的情况下，数学模型如图1所示。基于流体动力学原理，列出图中相关参数之间的关系：①F2=p1A1-p2A2；②p1=p′-R1Q112；③p2=R2Q212；④v=Q11/A=Q21/A。这4个等式构成模型方程组，经过带入、消除其中某些参数之后可得出变换后的无泄漏故障时的液压缸模型动力方程：

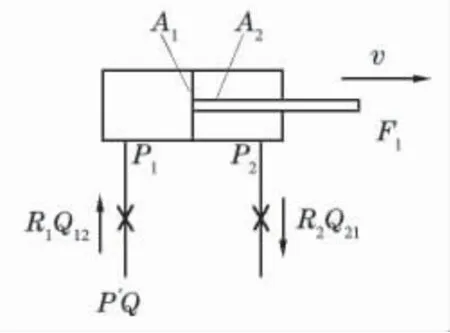
图1 无泄漏事故时的液压缸模型

在液压缸出现泄漏事故之后，数学模型如图（2）所示。对应的方程组：①F2=p1A1-p2A2；②p1=p′-R1Q112；③p2=R2Q212；④Q11=Q12+Q；⑤Q21=Q22+Q；⑥v=Q11/A=Q21/A。经过变换后得出的各参数之间的关系为：

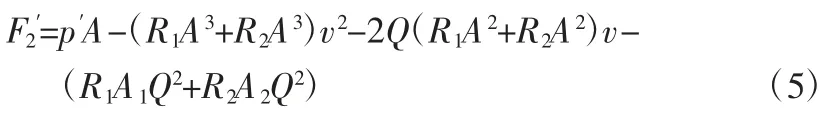
分析式（4）、式（5）可知，无论液压缸是否出现内泄漏事故，F 与v 之间的关系仍然为二次函数表达式（参数A 虽然为三次方形式，但并非主要参数，只考虑F 与v 即可）。对式（4）、式（5）进行深入分析后发现，机械液压缸中是否存在输出动力并不取决于p1是否＞p2。在此基础上，根据数学模型中的某些参数之间的相互关系，即可判断液压缸的泄漏情况。具体而言：第一，若p1＞p2，则Q＞0，此时，液压缸必定存在泄漏情况，泄漏方向与图2所示方向一致；第二，若p1=p2，则Q=0，表明液压缸处于正常运转状态，不存在内部泄漏情况；第三，若p1＜p2，则Q＜0，此时液压缸的流量方向与内泄漏方向（即图2 显示方向）相反。

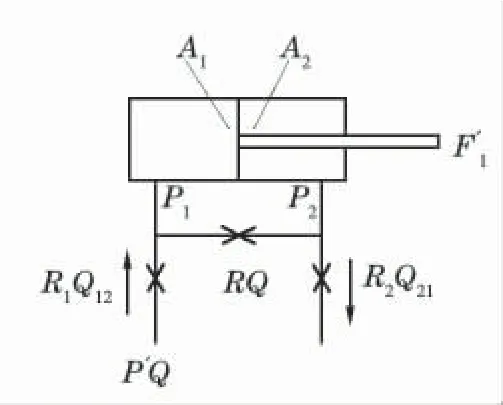
图2 出现泄漏事故时的液压缸模型

将式（4）、式（5）整理后得出：

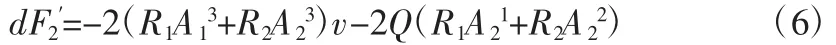
由上文所述可知，F 与v 之间的关系呈二次函数剖物线形态，且在液压缸内没有出现泄漏情况时，F2-V 与两条剖物线必定会在直角坐标系中的一个点位相交。将有关项合并之后，可得出：

2.3 液压缸内泄漏事故发生时的常见特性分析

再次对式（4）、式（5）进行分析后可以发现，当Q＜0 时，的绝对值必定会小于dF2/dv 的绝对值，且的曲线与的曲线在C 点相交。根据模型所示结果，当液压缸承受较大负载时（通常运行速度会有所降低），如果出现内泄漏事故，则液压缸的运行速度必定也随之降低（即同等负载下，无泄漏状态下的液压缸运行速度超过有泄漏事故时的运行速度）。

2.4 数学建模检测法的液压缸内泄漏故障检测实践分析

（1）首先正常启动液压缸，并将液压油加入油腔内。在此状态下，进油腔的压力逐渐升高，并能够与执行元件的负载保持平衡。受“油液具备可压缩性”这一特点的影响，进油腔产生的压力不会立刻达到与负载相同的水平，而是呈现出“渐变”的特性。实际结果显示，该过程的压力上升具有跳跃性。

（2）继续控制油液进入油腔，且需保证活塞可以平稳伸出，一直持续到活塞伸出到最大位置处（也可在执行元件的负载进入“无限大”时停止）。

按照上述流程，模拟液压缸未出现内泄漏、出现轻微内泄漏、严重内泄漏的情况，最终结果显示，基于数学模型的压力曲线变化情况存在差异。

3 结语

综上所述，本文基于数学建模法，将液压缸运行期间的各项参数设置为运行构成主参数，经过消除部分变量的转换之后，得出F 与v 之间存在二次函数关系。以此为基础，得出“同等负载下，无泄漏状态下的液压缸运行速度超过有泄漏事故时的运行速度”[3]的结论，试验结果表明该结论是正确的，表明基于数学建模的检验方法具备可行性。