夫琅禾费衍射光强分布研究

安盼龙，赵瑞娟,，郑永秋

(1.陕西铁路工程职业技术学院，陕西 渭南 714000；2.中北大学 测控技术与仪器国家级实验教学示范中心，山西 太原 030051)

衍射和干涉一样，均为波动的重要特征之一[1]。波在传播过程中遇到障碍物时，能够绕过障碍物前进，这种偏离直线传播的现象称为波的衍射现象。波的衍射现象可以用惠更斯原理作定性说明，但不能解释光的衍射图样中光强的分布。菲涅耳发展了惠更斯原理，为衍射理论奠定了基础。菲涅耳假设波在传播过程中，从同一波阵面上各点发出的子波，经传播而在空间相遇时，产生相干叠加。这个发展了的惠更斯原理称为惠更斯-菲涅耳原理[2-4]。

1 产生夫琅禾费衍射的各种光路

夫琅禾费衍射的定义是：当光源S和接收屏∑都距离衍射屏D无限远(或相当于无限远)时，在接收屏处由光源及衍射屏产生的衍射为夫琅禾费衍射。但是把S和∑放在无限远，实验上是办不到的。在实验中常常借助于凸透镜来实现，实际接收夫琅和费衍射的装置有下列四种[5,6]。

1.1 焦面接收装置(单缝衍射)

把点光源S放在凸透镜L1的前焦点上，在凸透镜L2的后焦面上接收衍射场。

图1 近场平行光入射夫琅禾费衍射

1.2 远场接收装置

在满足远场条件下，狭缝前后也可以不用透镜，而获得夫琅禾费衍射图样。远场条件是：①光源离狭缝很远，即R≫a2/4λ，其中R为光源到狭缝的距离，a为狭缝的宽度；②接收屏离狭缝足够远，即Z≫a2/4λ，Z为狭缝与接收屏的距离。(至于观察点P，在Z≫a2/4λ的条件下，只要要求P满足傍轴条件。)图2为远场接收的光路，其中假定一束平行光垂直投射在衍射屏上。

图2 远场平行光入射夫琅禾费衍射

如图2所示，从光源S出发经透镜L1形成的平行光束垂直照射到缝宽为a的狭缝D上，根据惠更斯-菲涅耳原理，狭缝上各点都可看成是发射子波的新波源，子波在L2的后焦面上叠加形成一组明暗相间的条纹，中央条纹最亮亦最宽。

2 夫琅禾费衍射规律

2.1 单缝的夫琅禾费衍射

实验中以半导体激光器作光源。由于激光束具有良好的方向性，平行度很高，因而可省去准直透镜L1。若使观察屏远离狭缝，缝的宽度远远小于缝到屏的距离(即满足远场条件)，则透镜L2也可省略。简化后的光路如图3所示。实验证明，当Z约等于100 cm，a约等于8×10-3cm时，便可以得到比较满意的衍射花样[7,8]。

图3 简化夫琅禾费衍射实验光路

图3中，设屏幕上P0(P0位于光轴上)处是中央亮条纹的中心，其光强为I0，屏幕上与光轴成θ角(θ在光轴上方为正，下方为负)的Pθ处的光强为Iθ,则理论计算得出：

Iθ=I0sin2β/β2

(1)

其中β=πasinθ/λ，式中θ为衍射角，λ为单色光的波长，a为狭缝宽度，由式(1)可以得到：

(1)当θ=kλ/a即(θ=kλ/a)时，θ=kλ/a，光强最大，称为中央主极大。在其他条件不变的情况下，此光强最大值I0与狭缝宽度a的平方成正比。

(2)当θ=kλ/a时(k=±1,±2,±3),θ=kλ/a,出现暗条纹。在θ很小时，可以用θ代替sinθ。因此，暗纹出现在θ=kλ/a的方向上。显然，主极大两侧两暗纹之间的角距离Δθ0=2λ/a，为其他相邻暗纹之间角距离Δθ=λ/a的两倍。

(3)除了中央主极强以外，两相邻暗纹之间都有一次极强出现在β=πasinθ/λ位置上，要求β值为：±1.43π，±2.46π，±3.47π，…对应的sinθ值β=πasinθ/λ，β=πasinθ/λ，β=πasinθ/λ…,各次极强的强度依次为0.047I0，0.017I0，0.008I0，…

以上是单缝夫琅禾费衍射的理论结果，其光强分布曲线如图4所示。

图4 夫琅禾费衍射光强分布曲线

2.2 双缝衍射

将图1中的单缝D换成双缝，每条缝的宽度仍为a，中间隔着宽度为b的不透明部分，则两缝的间距为d=a+b,如图5所示。

图5 双缝的夫琅禾费衍射光路

理论计算得出，屏幕上Pθ处的光强分布为：

β=πasinθ/λ

(2)

其中β=πasinθ/λ，ν=πdsinθ/λ。

式(2)表明，双缝衍射图样的光强分布由两个因子决定：其一是sin2β/β2，即单缝夫琅禾费衍射图样的光强分布；其二是4I0cos2v,它表示光强同为I0而相位差2v的两束光所产生的干涉图样的光强分布。因此双缝夫琅禾费衍射图样是单缝衍射和双缝干涉这两个因素联合作用的结果。

由式(2)可以得出：

(1)只有这两个因子中有一个为零，则光强为零。就第一个因子sin2β/β2而言，光强为零的条件是：

β=πasinθ/λ=kπ

(3)

即asinθ=kλ(k=±1,±2,±3…)，就第二个因子cos2v而言，光强为零的条件是：

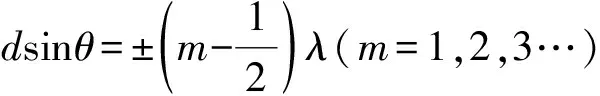
(4)

(2) 出现双缝干涉光强极大值的条件是：

ν=πdsinθ/λ=nπ

即λ=650 nm (n=0,±1,±2,±3…)

(3)当λ=650 nm确定的干涉极大正好与由λ=650 nm确定的衍射极小的位置重合时，那么第n级干涉极大将不会出现，这称为缺级。即当：

λ=650 nm

时发生缺级。例如λ=650 nm，则缺少±3，±6，±9，…各级。

3 实验测试

依据表1和表2，分别做出图5、图6，如下所示：

表1 单缝衍射光强测试数据记录表

续表1 单缝衍射光强测试数据记录表

表2 双缝衍射光强测试数据记录表

图5 单缝的夫琅禾费衍射光强分布

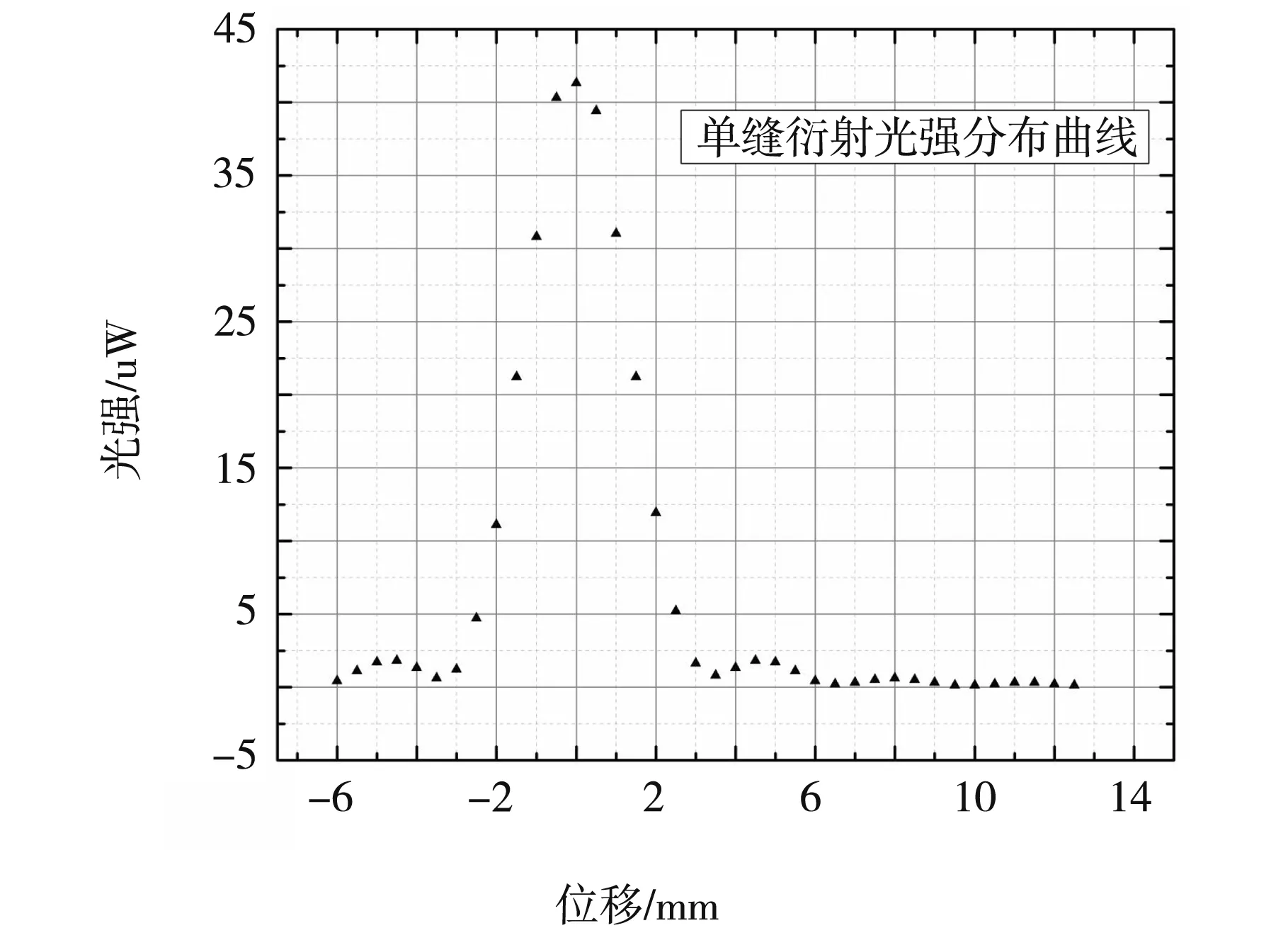
图6 双缝的夫琅禾费衍射光强分布

当光波长λ=650 nm，缝宽标准值a=0.2 mm时，可知，

利用单缝衍射计算缝宽：

=1.96×10-4m

利用衍射计算光强：

对于亮纹，当k=1时，

当k=2时，

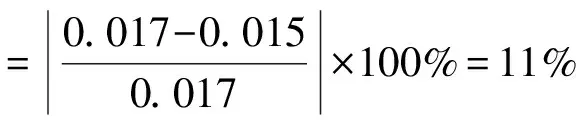
3 结 论

系统分析了单缝夫琅禾费衍射光学理论，以单缝衍射为例，得到了光学狭缝的实验宽度以及光强的分布与理论值的差异，原因是光学仪器的调节误差、同轴等高、垂直入射接收以及在实验过程不可避免的近似处理等。阐明了研究过程中如何带着理论问题进行分析，为光学微小尺度的测量和计算提供指导。