基于模糊滑模控制的塑料挤出机温度控制系统设计
高 源 赵 龙 庞 浩 冯 晗 罗永刚
(1.山东理工大学 电气与电子工程学院,淄博 255049;2.国网山东省电力公司昌乐县供电公司,潍坊 262400)
塑料管道制品由于其质量轻、耐腐蚀、易生产等特点,被广泛应用于各个行业。随着工业自动化的发展,塑料管道的挤出生产日趋自动化、智能化,而其中的塑料挤出机(挤塑机)是塑料挤出生产走向自动化、智能化的核心设备。在挤塑机工作过程中,对于塑料熔体温度的控制精度是反映挤塑机质量的关键指标,因为其温度控制系统具有大惯性、时滞性及非线性等特点[1],所以降低了系统的快速调节能力和稳态精度。以树脂材质(Polyvinyl Chloride,PVC)塑料管道的挤出生产为例,温度过高会使熔体分解,过低则会产生颗粒,影响成品质量,因此生产过程中熔体温度应在195~205 ℃。传统工业对挤塑机温度控制多采用比例积分微分系统Proportion Integration Differentiation,PID)控制,但其控制过程中Kp、KI、KD参数不会随着系统结构的变化而改变,且由于积分环节的作用,控制过程中会产生较大的超调现象[2-3]。传统滑模控制(Sliding Model Control,SMC)通过选择合理的滑模面,可以使系统运动点在滑模面附近运动,但因为其趋近速率无法随系统的改变进行动态调整,所以其系统运动点在滑模面附近时也有较大的趋近速率,因此会产生较大的抖振,无法满足挤出生产对控制精度的要求[4-5]。
针对挤塑机温度控制精度与加热速度的要求,研究人员展开了广泛的研究。冯润根提出了一种模糊神经网络PID 控制[6],成功使挤塑机温度从220~260 ℃的升温时间缩短到了200 s 以内,且可以较好的抑制超调现象;迟晓妮提出了单神经元自适应PID控制的注塑机温度控制系统[7],使注塑过程中0~250 ℃的升温时间缩短到了300 s 以内,但是对超调现象的抑制效果不强;凌志梅将自适应滑模控制应用于挤塑机温度控制系统中[8],使温度超调量减小到了0%,且温度的平均误差减小到了0.82 ℃,但调节时间增加到了20 min。
为提高挤塑机温度控制的精度,缩短其调节时间,本文提出了一种模糊滑模温度控制系统。该系统能够利用模糊算法分析温度误差及其变化率之间的关系,从而实时计算滑模控制的趋近速率,在较小的温度误差下,可以获得较小的趋近速率,减小超调,同时抑制抖振;而在较大的温度误差下,可以获得较大的趋近速率,缩短调节时间。
1 塑料挤出机温度控制系统数学模型
塑料挤出机机筒的结构原理图如图1 所示。其工作过程为:在加热线圈的作用下,物料(塑料原料颗粒)被加热至熔融状态,同时驱动电机带动螺杆旋转,产生沿机筒方向的轴向推力,将熔融状态下的物料从口模处挤出,初步形成高温的塑料管,再经冷却、缠丝、卷捆等工序生产出成品塑料管。
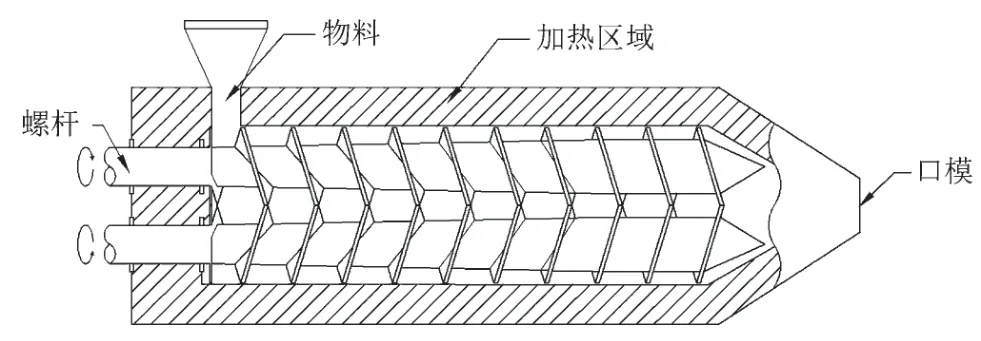
图1 挤出机机筒结构
挤塑机温度控制系统的数学模型具有二阶系统的特点,同时因为温度系统具有较大的滞后性,所以采用带大滞后项的二阶系统来表示挤塑机温度控制系统的数学模型:
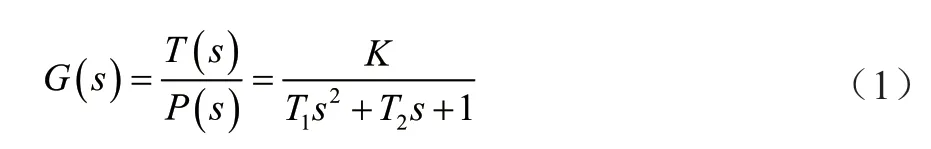
式中:K为增益;T1、T2为常数,由系统参数决定;T、P分别为模型的输出温度和输入功率。
为验证模型是否符合实际经验,模型的阶跃响应如图2 所示。其中,T1=3 200;T2=130;K=21。给该数学模型加入阶跃信号,验证其在输入功率P为10 kW 时,温度的变化曲线,结果表明,t=342.7 s 时,温度能够达到预期的200 ℃。
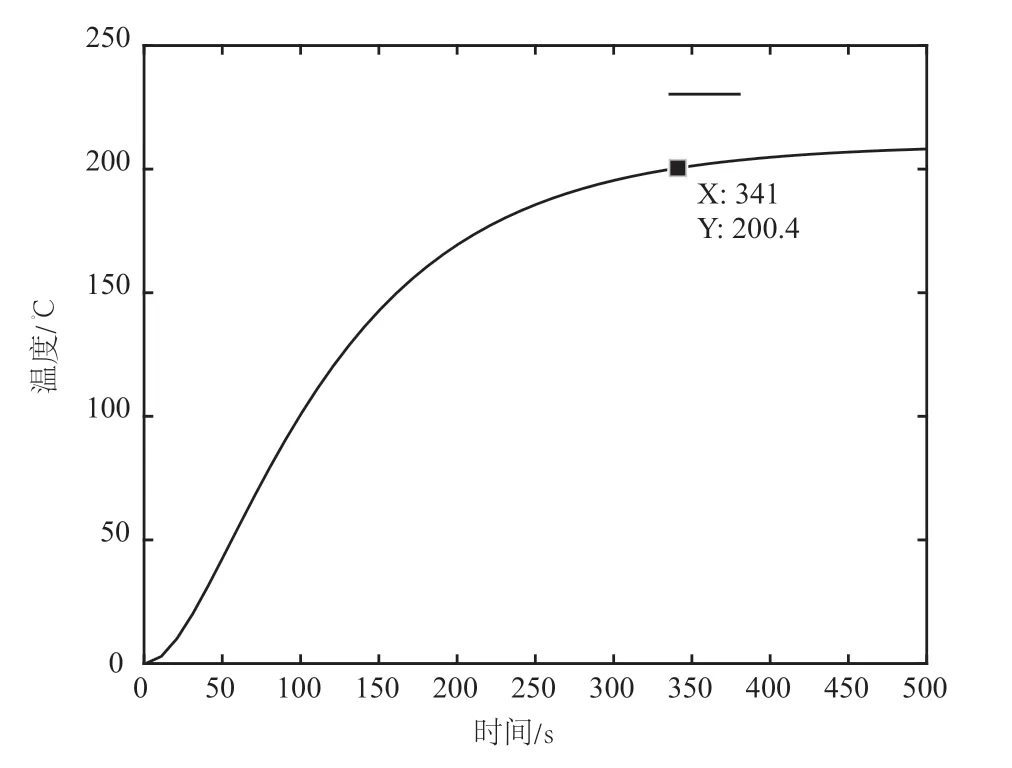
图2 数学模型阶跃响应
2 塑料挤出机温度控制系统结构
在传统PID 控制下,系统会产生较大的超调量,最高温度可达280 ℃左右,调节时间约为300 s。在此期间所产出的塑料管无法满足生产质量的要求。在传统生产模式中,若要提升系统性能,则需依靠经验手动调整Kp、KI、KD的参数,调节过程复杂且精度不高,降低了设备的自动化水平。
为提升系统控制性能,现利用滑模控制的强鲁棒特性改进挤塑机的控制系统:一方面,采用滑模控制取代传统PID 控制,并通过设计合适的滑模面,迫使系统的运动点在滑模面附近滑动,使其以最快的速度逼近系统的稳定点;另一方面,趋近过程中,采用模糊控制器不断优化趋近速率,使温度误差较大时,系统的运动点能够以更大的趋近速率运动到滑模面。挤塑机模糊滑模温度控制系统的结构图如图3所示。
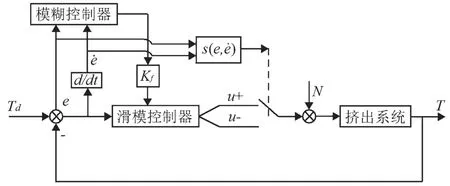
图3 挤塑机模糊滑模温度控制系统结构图
2.1 Fuzzy 控制器设计
2.2.1 输入输出变量论域
采用温度误差e及其变化率e作为模糊控制器的输入,并将模糊控制器的输出定义为Δε,然后设定温度200 ℃为给定值,将温度误差分为5 段论域,即{-20 ℃、-10 ℃、0 ℃、10 ℃、200 ℃},再将温度误差变化率分为5 端论域,即{-20 ℃•min-1、-10 ℃•min-1、0 ℃•min-1、10 ℃•min-1、20 ℃•min-1},输出Δε的5 段论域为{1、0.75、0.5、0.25、0},则系统输入输出的模糊语言为:

2.2.2 隶属度函数
输出Δε和两个输入的绝对值(|e|、|e|)较小时,采用高斯型隶属度函数:

式中:cg、σ为系数,分别决定函数中心点的位置和曲线宽度;x为模糊输入输出元素值。
输入的绝对值(|e|、|e|)较大时,采取Z型、S型隶属度函数:

式中:a、cs为系数。
控制规律依据如下经验:如果|e|、|e|较大,则应增大趋近速率ε,反之减小ε。据此经验设计的规则表如表1 所示。
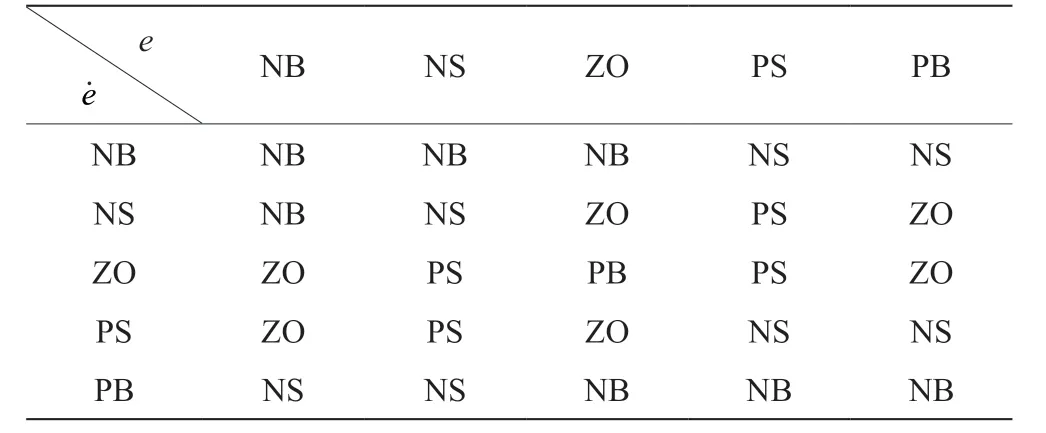
表1 模糊控制规则表
2.2.3 清晰化规则
解模糊过程采用最大隶属度平均值法[10-11]:

式中:xi取各隶属点的最大值。
最后按比例放大模糊控制器的输出值,放大系数为Kf,由此得到优化后的滑模趋近速率为:

2.3 SMC 控制器设计
将系统数学模型写成微分方程的形式为:
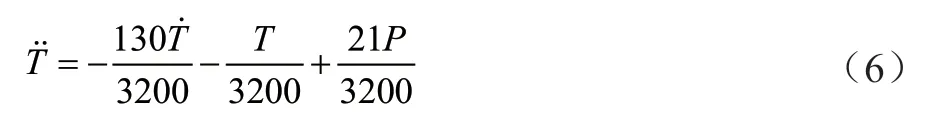
式中:T为塑料熔体温度;P为加热功率。
采用微分滑模面的计算方式为:

式中:λ为系数,e为温度误差变量。
对式(6)两边求导可得:

采用带有指数函数的趋近率:


式中:u为滑模控制器的输出,取u=P。
判断Lyapunov 稳定性时,设Lyapunov 函数为:

式中:V为李雅普诺夫算子。
由式(10)可得:

结果满足李雅普诺夫稳定性判据,系统稳定于s=0 处。
3 仿真验证
在MATLAB-Simulink 环境下仿真验证本文设计的模糊滑模温度控制系统,系统各参数选取如下[12]:λ=5;k=30。模糊滑模控制仿真结果如图4 所示。在t=330 s 时为系统加入幅值为5 的高斯噪声扰动:

式中:τ、h、w为高斯函数系数;τ=330;w=10;h=5。
由图4 可知,在模糊滑模控制作用下,系统的温度在0~100 s 时迅速上升,且在130 s 时有较小的超调(最高温度<200.3 ℃);而在传统PID 控制的作用下,温度超调较大,最高温度达到了280 ℃左右。调节时间方面,模糊滑模在150 s 后,系统温度逐渐稳定于199.8 ℃左右;而传统PID 控制经过约350 s的时间,系统温度才逐渐稳定。
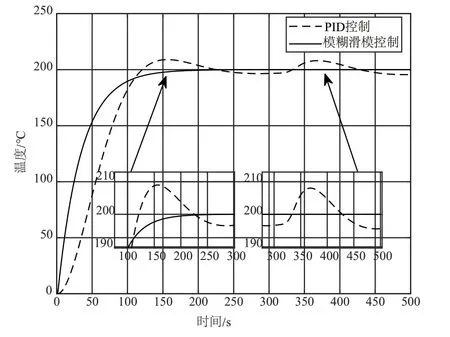
图4 模糊滑模控制下温度曲线
模糊滑模控制下输出温度放大图如图5 所示,由图5 可知,在模糊控制的调节作用下,挤塑机模糊滑模温度控制系统输出温度的抖振情况被抑制到了5×10-4℃以内。
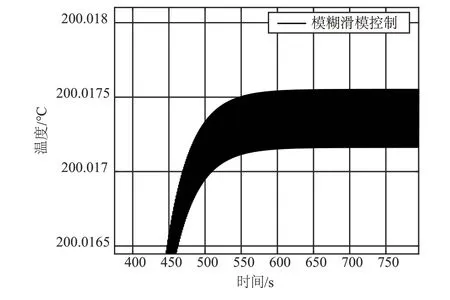
图5 模糊滑模控制下输出温度放大图
4 结语
本文针对挤塑机的温度控制系统设计了模糊滑模控制的方法,并用较大惯性系数的二阶传递函数模型近似描述了具有较大滞后特性的挤塑机温度系统数学模型。通过模糊控制方法计算温度误差及其变化率后,得出适合当前系统状态下滑模控制所需的趋近速率,以此优化传统滑模控制,能使其在大偏差下获得较大的趋近速率,同时在小偏差下减弱系统抖振,从而提升控制系统性能。为验证系统的性能,在MATLAB/Simulink 中对系统进行了仿真分析,并对比了传统PID 控制,结果表明,本次设计的挤塑机温度控制系统具有动态响应速度快和无超调量的特点。

