基于支持向量机的时域虚拟路谱评价方法
李文魁 邱宇 陈海江
(上海汽车集团股份有限公司技术中心,上海 201804)
主题词:虚拟路谱 评价 高斯核函数 支持向量机
1 前言
相比于传统的传感器式路谱采集,虚拟路谱具有成本低、周期短等优势,已经广泛用于汽车数据采集和疲劳耐久分析[1-4]。
路谱是台架试验和计算机仿真的输入,为了确保试验和仿真的准确度,路谱的准确度尤其重要[5],虚拟路谱与实车路谱的差异性评价也十分关键[6-7]。
路谱时域信号的评价方法主要分为主观评价和客观评价。主观评价主要依靠工程师的经验进行判断,或者根据行业内建立的准则进行打分,这种方法需要有经验的工程师花费大量的时间。客观评价的主要手段是对时域信号进行统计学分析[8],利用客观统计量进行评价,这种方法的准确度不是很高,易出现统计量差异很大,但实际路谱差异在接受范围内的情况。
本文针对主、客观评价的问题,利用监督学习的思想,提出一种将主观评价和客观评价的优点进行结合的虚拟路谱评价方法,将原始路谱信号和预测路谱信号客观统计量差值的百分比作为特征数据,以多位有经验工程师的主观平均分作为标签数据,根据虚拟路谱和实际路谱的差异评分,并以此数据集为基础,利用支持向量机(Support Vector Machine,SVM)算法进行拟合[9],获得虚拟路谱评分模型。
2 特征值的创建与处理
2.1 特征值创建
为了描述时域信号,本文基于统计值创建了最大值、最小值、均方根、极差、损伤、时域均方根误差、频域均方根误差、标准差、方差、峰值因子、50%最大值以上的均方根误差、50%最小值以下的均方根误差、75%最大值以上的均方根误差和75%最小值以下的均方根误差共14个特征值。
为了方便比较,设特征值为:
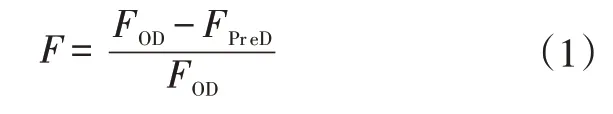
式中,FOD、FPreD分别为原始信号和预测信号的统计值。
2.2 特征值处理与筛选
主观评分与特征值的相关性关系到模型的准确性,本文对主观评分的平均值和特征值的相关性进行分析,结果如图1所示。
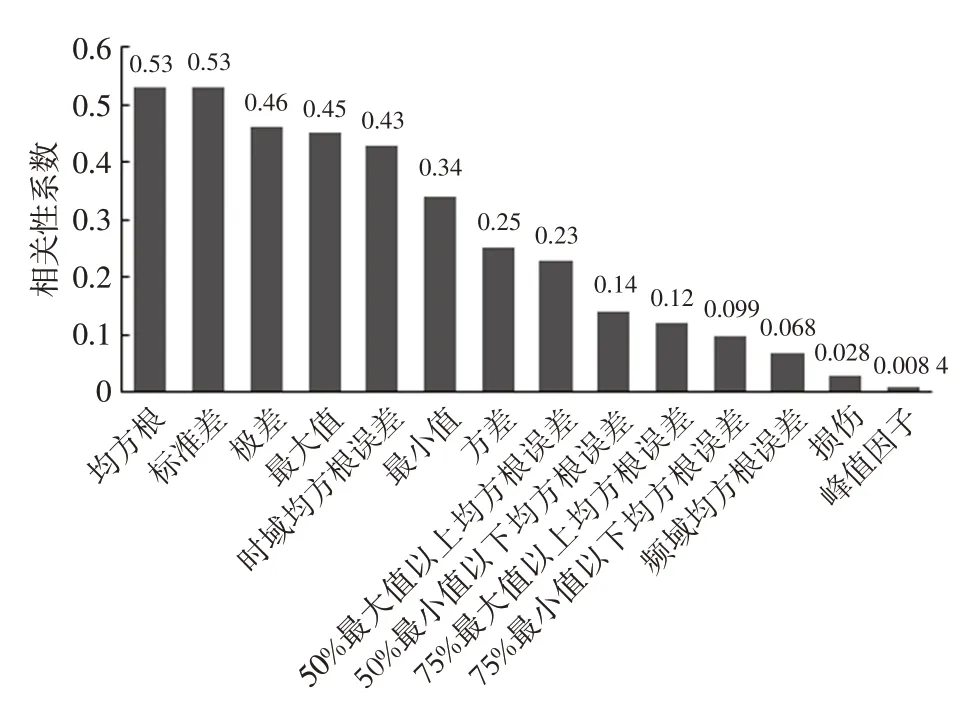
图1 主观评分与各特征值的相关性系数
由图1 可以看出,均方根和标准差与主观评分的相关性系数相等,原因是在时域信号均值为0 的情况下两者是相等的,本文选用的时域信号经过了均值归零处理,所以两者的相关性为1。因为路谱的损伤统计值可以直观地反映测试零件在路谱激励下的疲劳寿命累计速度,所以在评价虚拟路谱时会着重比较虚拟路谱与实际路谱的损伤值差异。通常,信号的大幅值部分对损伤的贡献量较大,50%最大值以上的均方根误差、50%最小值以下的均方根误差、75%最大值以上的均方根误差、75%最小值以下的均方根误差等特征都是为了描述虚拟路谱与实际路谱损伤值的差异而创建的。同时,从图1 中可以看出,损伤特征值的相关性较低,而损伤特征值在疲劳损伤容限分析中非常重要,也是工程师评估时域信号时的重要参考内容,造成相关性较低的原因可能与不同信号幅值的数量级相差过大有关。
图2 所示为对损伤特征值做不同处理后与主观评分的相关性系数,经对数处理后,损伤特征值与主观评分的相关性系数没有明显提升,反而出现了下降,这主要是损伤的数量级差别过大引起的,为了消除这一影响,选择对时域信号进行处理。将实际路谱信号和虚拟路谱信号的数据点同时除以实际路谱信号的最大值进行归一化,然后对归一化的时域信号提取特征值,并对损伤特征值进行对数处理,发现只进行归一化处理的相关性与未处理时相同,而归一化处理并进行对数处理后,损伤特征相关性明显提升。
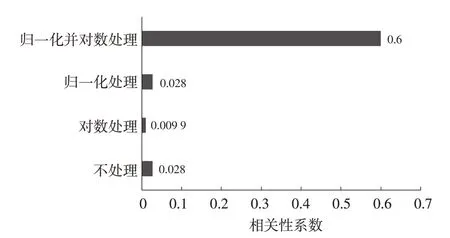
图2 不同处理方式下的损伤相关性对比
根据相关性系数的大小,本文选用最大值、最小值、均方根(RMS)、极差(Range)、损伤、时域均方根、频域均方根、方差、50%最大值以上的均方根误差、50%最小值以下的均方根误差这11个特征值作为训练特征。
3 支持向量机建模
由于数据集不是线性可分的,本文采用带有高斯核函数(Radial Basis Function,RBF)的支持向量机作为拟合算法,并通过网格搜索法来寻找惩罚系数C和内核系数σ的最优组合,使得决定系数R2最大。首先,对训练用的数据集进行预处理和数据分割。将上述信号的特征值和评分作为建模的数据集,对数据集的特征值进行标准化处理,处理成均值为0、方差为1 的特征值,将70%的数据集作为训练数据集,其余30%的数据集作为验证数据集。然后,将训练数据集带入算法进行训练,并用R2作为模型的评价指标,由于模型的R2取决于模型的双变量值,同时指定惩罚系数C和内核系数σ的取值范围,使用网格搜索的方法,寻找R2最优的模型参数。为了增强模型的泛化能力,采用交叉验证的方法进行训练。最后,利用验证数据集来验证模型的精度,观察其与训练值差别是否过大。建模流程如图3所示。
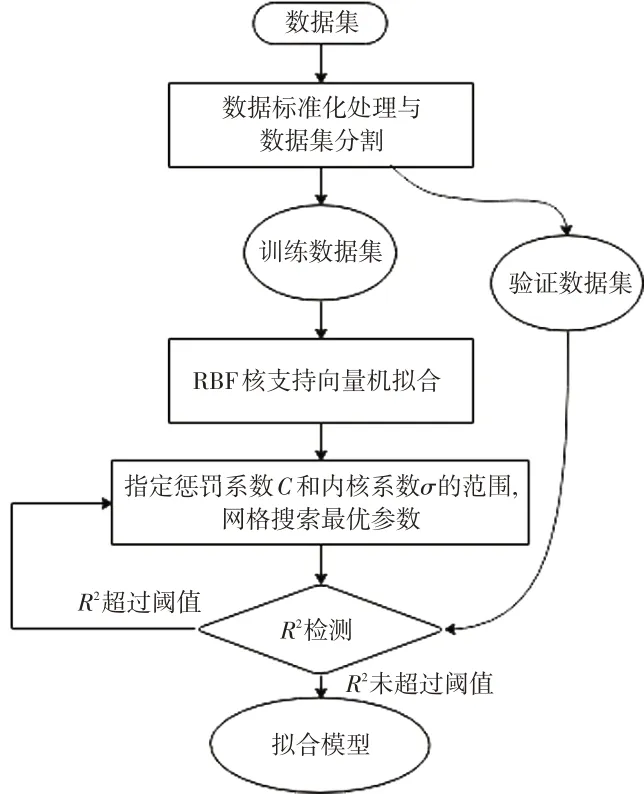
图3 建模流程
模型质量的评价指标决定系数R2定义为:
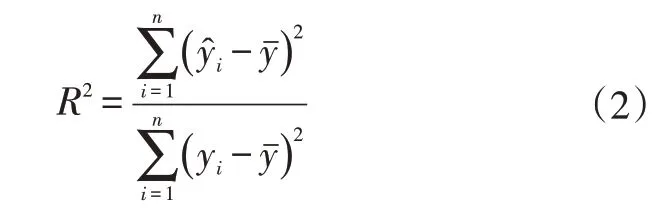
R2∈[0,1],越接近1说明拟合效果越好,可认为R2>0.6的模型可以使用,R2>0.8的模型拟合度较好[10]。
4 建模结果分析
4.1 时域信号统一建模
将路谱信号不加区分当作一个整体,处理好的客观统计值作为数据集的特征,主观评分作为标签,采用带有RBF 的支持向量机拟合模型,通过网格搜索寻找最优的模型参数,图4所示为根据网格搜索的结果作出的等高线,为了寻找准确的全局最优参数,先大范围搜索最优参数,然后根据搜索的图形,在R2较高的区域再进行一次网格搜索。经过2次网格搜索,模型在C=11.12、σ=2.51处,R2达到最大值0.77。
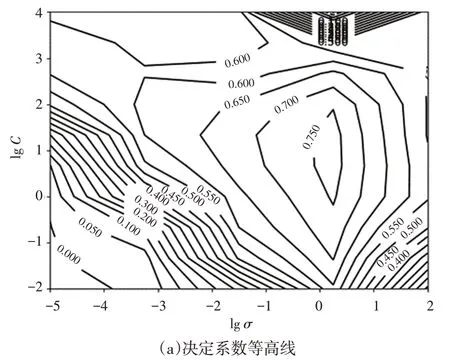

图4 网格搜索结果
R2结果满足精度的要求,但是在进一步对不同类型的信号分开打分时却发现不同信号之间的R2差异较大,结果如表1 所示。其中加速度和应变信号的R2较大,其他类型信号的R2较小低,说明这种数据信号不加区分的统一模型在单独预测某一类信号时泛化能力较弱,产生了过拟合的现象。

表1 统一建模的R2结果
本文将采用的时域路谱信号分为5 种类型,如表2 所示,各类信号的单位和性质不同,且信号的量级也存在较大差异,导致建立统一的预测模型在预测不同的信号类型时R2差异较大。故本文建立一种按照信号通道类型划分的独立预测模型,通过对比2 种建模方法的验证结果决定最终的虚拟路谱评价方法。

表2 通道信息
4.2 时域信号分开建模
5 种类型信号的模型参数与R2如表3 所示,并用建立的模型来预测新的数据集,比较模型预测评分与测试模型的预测效果。
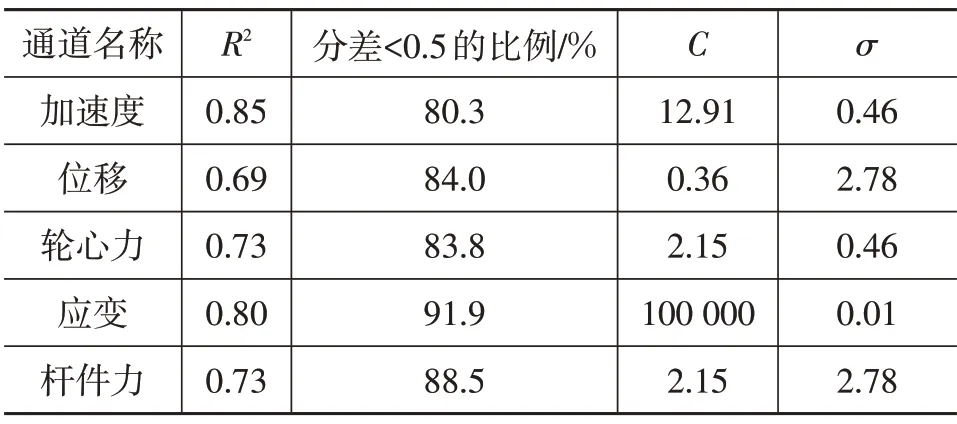
表3 分开建模结果
图5 所示为不同类型信号建模后模型打分与真实打分的分差分布情况,设差值不超过0.5分为优秀,不超过1分的结果可以接受。
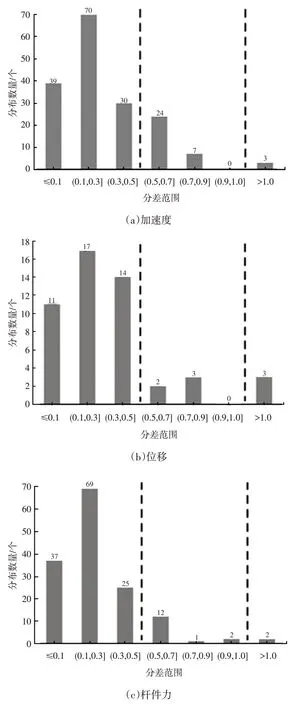
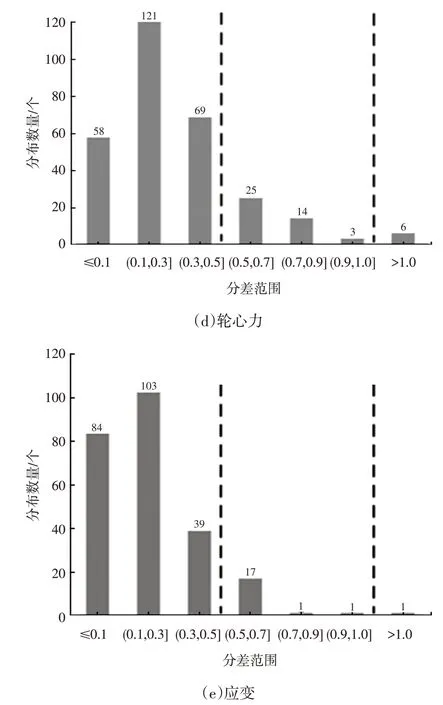
图5 不同信号模型的分差分布
为了确定2 种建模方法的差异,比较2 类模型预测不同类型信号数据的R2,结果如表4所示。
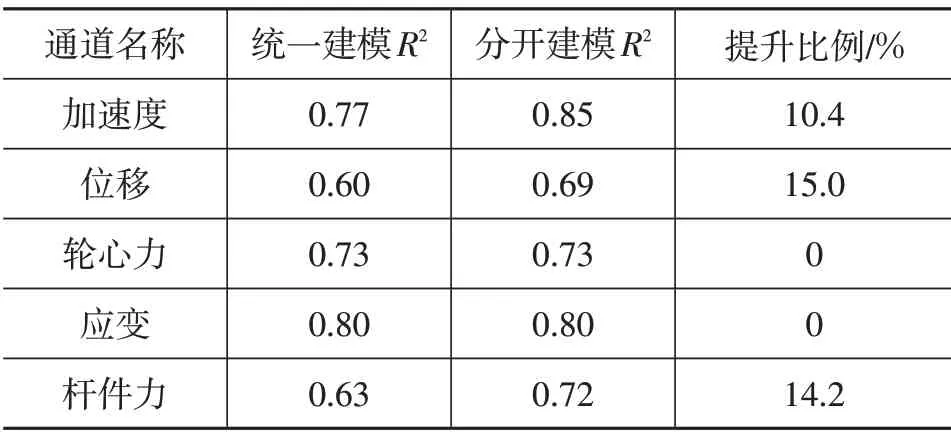
表4 建模结果比较
从表4中可以看出,分开建模的R2除轮心力和应变信号外,其余3种类型信号均比统一建模高。考虑到建模精度的优势,本文选用不同信号类型分开建立的模型作为虚拟路谱的评价模型。
随机挑选1 000 个虚拟路谱,按照信号类型的不同进行分类,利用上述的模型进行打分,分差不超过0.5的比例对比结果如图6 所示,预测得分的对比结果如图7所示。
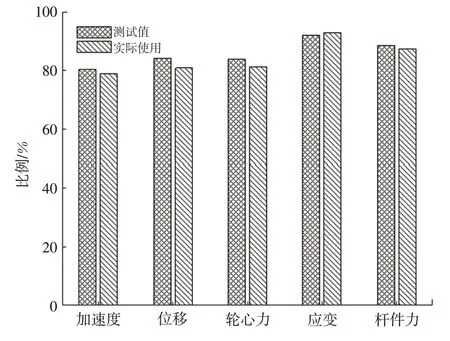
图6 分差不超过0.5分的比例对比
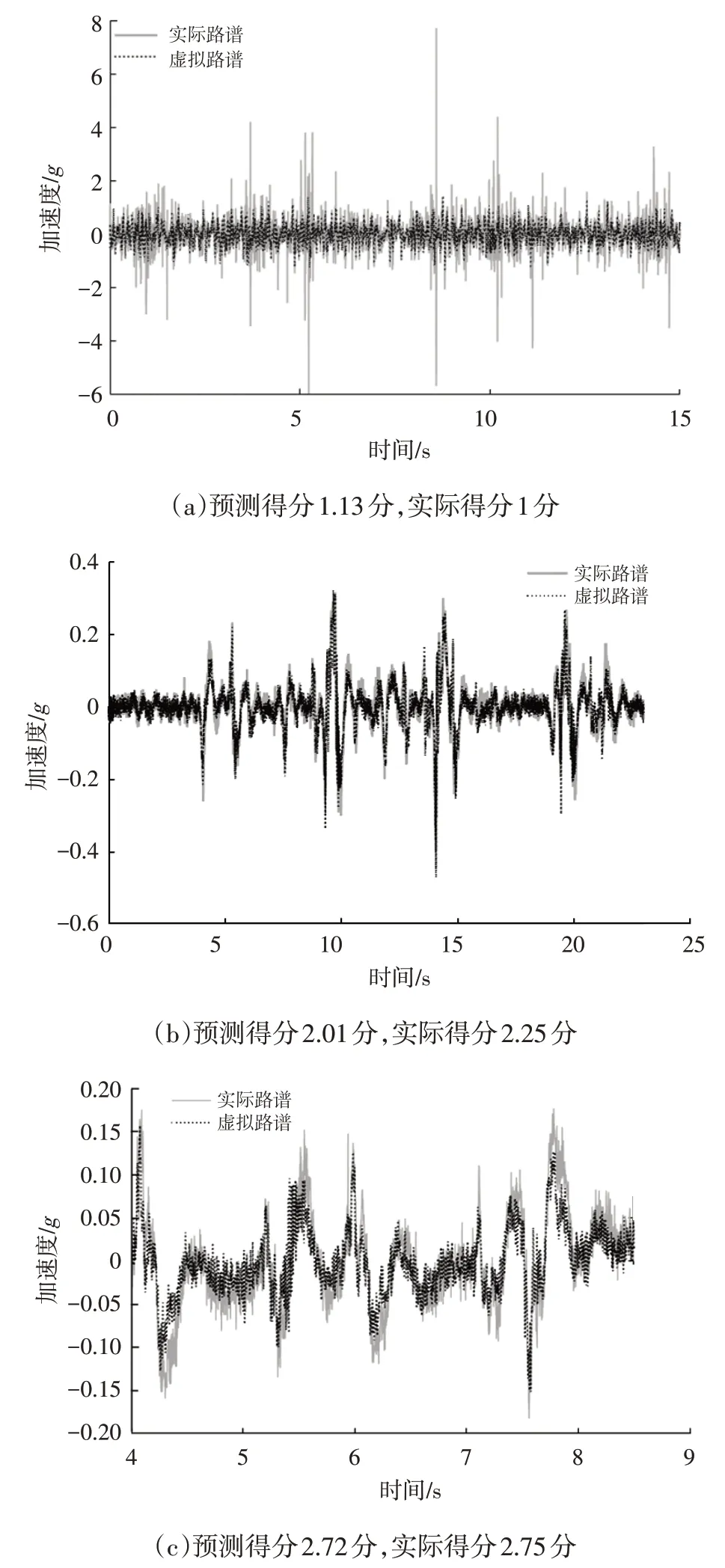
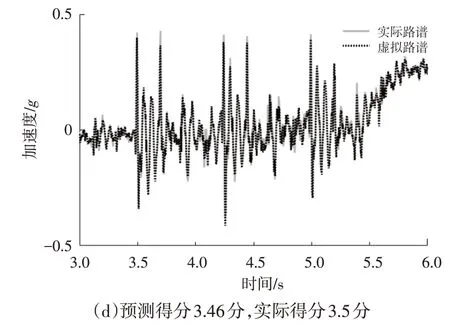
图7 模型评价效果
从图6可以看出,对1 000个虚拟路谱打分时,与主观评价结果差值不超过0.5分的比例与建模测试时基本一致,说明本文建立的模型拥有良好的泛化能力。从图7 可以看出,模型具有良好的打分精度,本文所建立的虚拟路谱预测模型可以有效评价虚拟路谱与实际路谱间的差异,提高虚拟路谱评价的效率和准确性。
5 结束语
本文提出了一种基于高斯核函数的支持向量机算法的虚拟路谱评价模型。首先,从客观统计值中提取时域信号的特征值,并将特征值与利用工程师主观评分作为数据标签相结合构建数据集。之后,将数据集分割为训练集和验证集,将训练集代入训练算法中,利用网格搜索的方法来搜索模型的最优参数,并用验证集来验证模型的决定系数R2是否达到标准。最后,用建立好的模型对虚拟路谱进行评分,结果表明,本文所建立的模型能有效评价虚拟路谱与实际路谱之间的差异。
本文提出的虚拟路谱评价方法实际上是一种评价2条时域信号的方法,其利用场景不只局限于虚拟路谱评价,也可以评价台架的路谱迭代精度等。

