基于“构造法”的高中数学解题思路分析

何晨良

(江苏省无锡市第一中学 214041)

数学研究中，存在非构造性数学和构造性数学，主要讨论存在和构造的问题.利用构造法能简化许多题目的解题步骤，教师帮助学生掌握解题基本方法和巧妙思路，设置有探究性、开放性、情境性、应用性的数学题，切实提升学生的解题能力.

一、把握本质，解决变式题目

所谓变式题目，指的是从一个题目出发，经过改造和转变产生不同的题目.学生在解题中会碰到较多变式题目，只有有效分析变式问题的形式、内容和结论，分析问题的本质属性，才能有效解决问题.学生在解决变式问题的过程中，也能逐渐突破题目形式的干扰.对于变式问题，应认清本质、灵活分析.

例1如果把所有正整数排成一个三角形阵列，那么如图1，第n行从左向右查，第三个数字是____(n≥3).

分析根据图式发现，第一行有1个数字，第二行有2个数字，第n-1行一共有n-1个数字，所以第n-1行最末尾的数字正好是等差数列中的第n-1项.

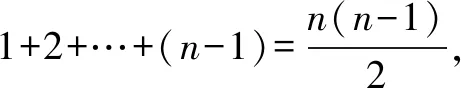
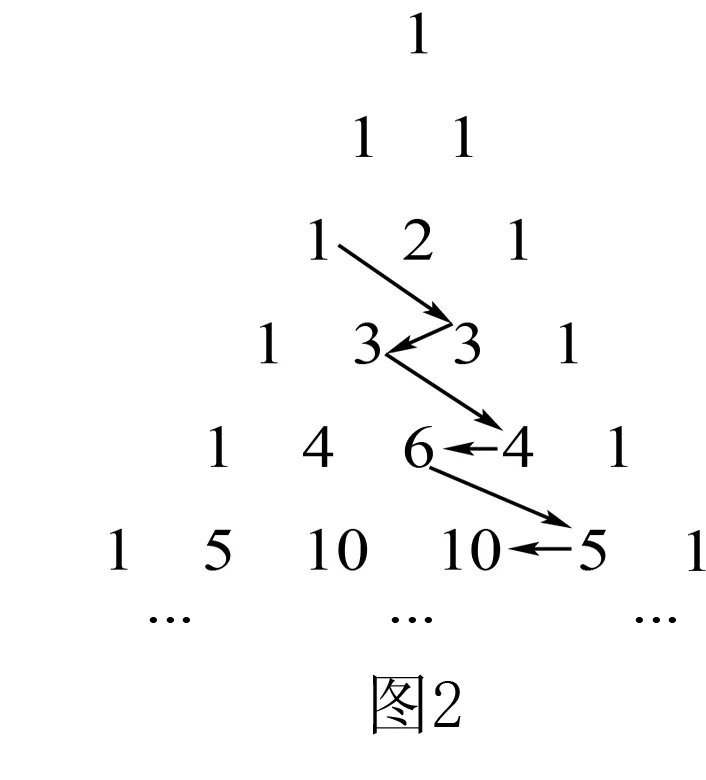
例2 在如图2中的杨辉三角里面，l斜线的上方有一个锯齿形数列，这个数列是：1，3，3，4，6，5，…，如果第n项是an，那么a19的数值是多少？

例3有一个n行n列的矩阵A，是n2(n∈N*，同时n≥4)个正数组成的，这个矩阵A如下：

a11a12…a1n

a21a22…a2n

… … … …

an1an2…ann

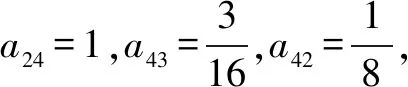
分析这个变式题目是在前面题目基础上引入了矩阵，而且包含等比数列和等差数列.此题看似结构比较复杂，而且内容比较长，但是如果能捋顺思路、仔细分析，可以有效解决问题.

二、一题多解，多角度分析问题

一些高中数学问题有多种解法，可以从不同侧面看待问题和分析问题，通过发掘题目中已知和未知的关系，尝试使用不同方法和思路解题是培养学生发散思维和拓展解题思路的重要途径.

分析1 斜率公式的构造.

因为0<α<β，所以在第一象限中，P(α,β)必然在y=x这条直线的下方.

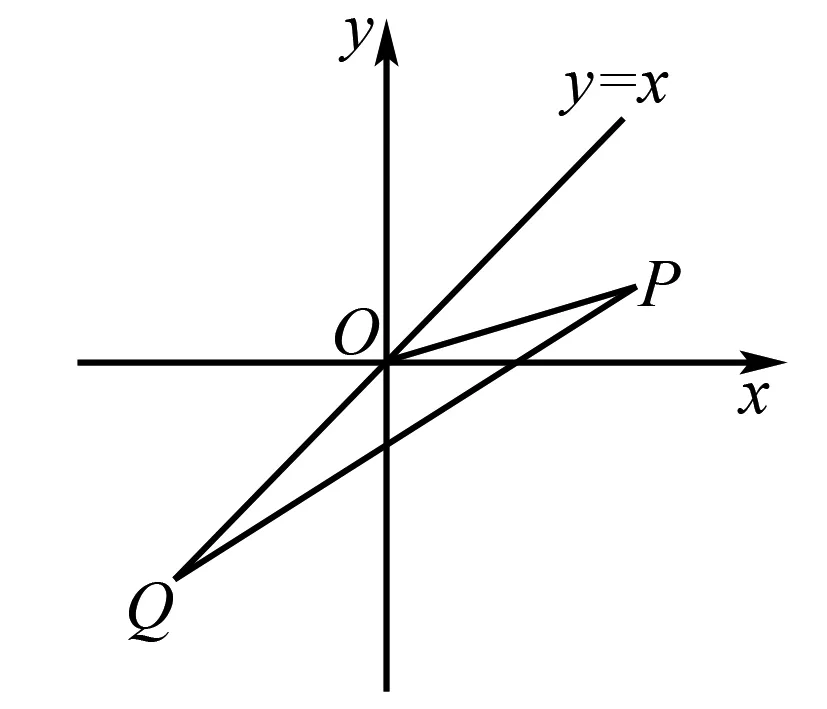
图3

使用构造图形的方式，分析具体问题，采用图形辅助对象解决问题.

分析2辅助函数的构造.

对比题干中两边的不等式，可以发现左边比右边只是多出一个γ，所以采用构造辅助函数的方式解决问题：

分析3 现实模型的构造.

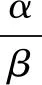
三、构造复数，巧妙解决数学问题

构造复数是常用的方法，学生通过推断、猜测、比较和分析探索构造思路，进而巧妙解决问题.

例5 已知sina+sinb=y，cosa+cosb=x，同时x2+y2≠0，求解tan(a+b)是多少？

分析这个题目可以使用sin2b+cos2b=1，sin2a+cos2a=1来求解，但是具体求解过程比较复杂，利用构造复数的方法能简化问题.首先观察题目中的已知条件，而后联想到函数相关的知识，用构造复数方式巧妙解决问题.复数有三角、几何、代数等表达方式，和高中数学的知识紧密联系，使用复数模型的运算法则和性质解题.

设z2=isinb+cosb，z1=isina+cosa，那么|z2|=|z1|=1.

同时，z2+z1=i(sina+sinb)+(cosa+cosb)=yi+x.

同时，z1z2=isin(a+b)+cos(a+b).

因为|z2|=|z1|=1,

因为a2+b2≠0，所以a,b不都是零.

乍一看这个题目，一些学生可能被唬住，但是构造复数能完美解决问题，复数有三角、几何、代数等多种形式，有着明确的运算法则和性质.对于一些难以解决的代数问题，使用构造复数的方式，能创造性解决问题，解题过程比较简单.

使用构造法能简化许多题目，但是需要注意，这种方法不是万能的.在高中数学解题过程中，如果刻意寻求和模仿，只会让解题过程更加繁琐.要明确构造法的局限性，把握数学问题的本质，采用合理解题步骤.在解题训练中，可以兼用常规方法和构造法.构造法虽然使解题步骤更少、更简单，但是挑战性更强，可以节约较多时间，让快速解决高中数学问题成为可能.