由一道适应性模拟考试题引发的思考
胡连冬
(湖南省长沙市宁乡市第七高级中学 410635)
一、联系实际,提出问题
2021年元月全国八省组织了第一次高考前的适应性模拟联考,这也是新高考在考试录取方面进行首轮 “现场练兵”;其中湖南省的物理卷有这样一道选择题.

题目如图1,一根质量为m的匀质绳子,两端分别固定在同一高度的两个钉子上,中点悬挂一质量为M的物体.系统平衡时,绳子中点两侧的切线与竖直方向的夹角为α,钉子处绳子的切线方向与竖直方向的夹角为β,则( ).
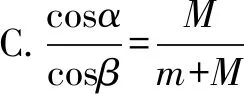
这道题以生活中真实问题情境为载体,考查考生的理解能力、建模能力、分析推理能力,是一道突出“素养导向”考查“关键能力”的好题.在评卷中笔者发现本题得分率很低,究其原因是考生对研究对象选取不当,缺乏将实际问题转化为物理模型的能力.
“绳子”是高中物理力学中常见模型,其中“轻绳”是理想化模型,轻绳的质量不计,轻绳产生弹力时呈直线,且同一根轻绳上各处弹力大小相等,弹力方向沿轻绳收缩的方向;而本题的绳子具有一定的质量,那么,实际生活中承载重物的绳子产生弹力时能呈直线吗?绳上各处弹力大小相同吗?实物绳子究竟有怎样的力学特征呢?下面结合本题作简要分析.
二、突出建模,解决问题
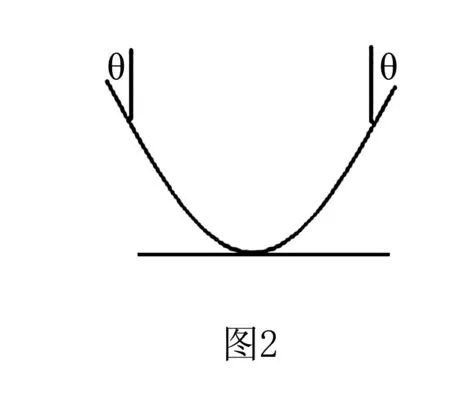
如图2所示,一根质量为m的匀质绳子,两端分别固定在同一高度的两个钉子上.平衡时,绳子中点的切线水平,两侧绳子的切线与竖直方向的夹角为θ,求钉子对绳子的拉力和绳子中点处产生的弹力.

①
F2sinθ=F1
②
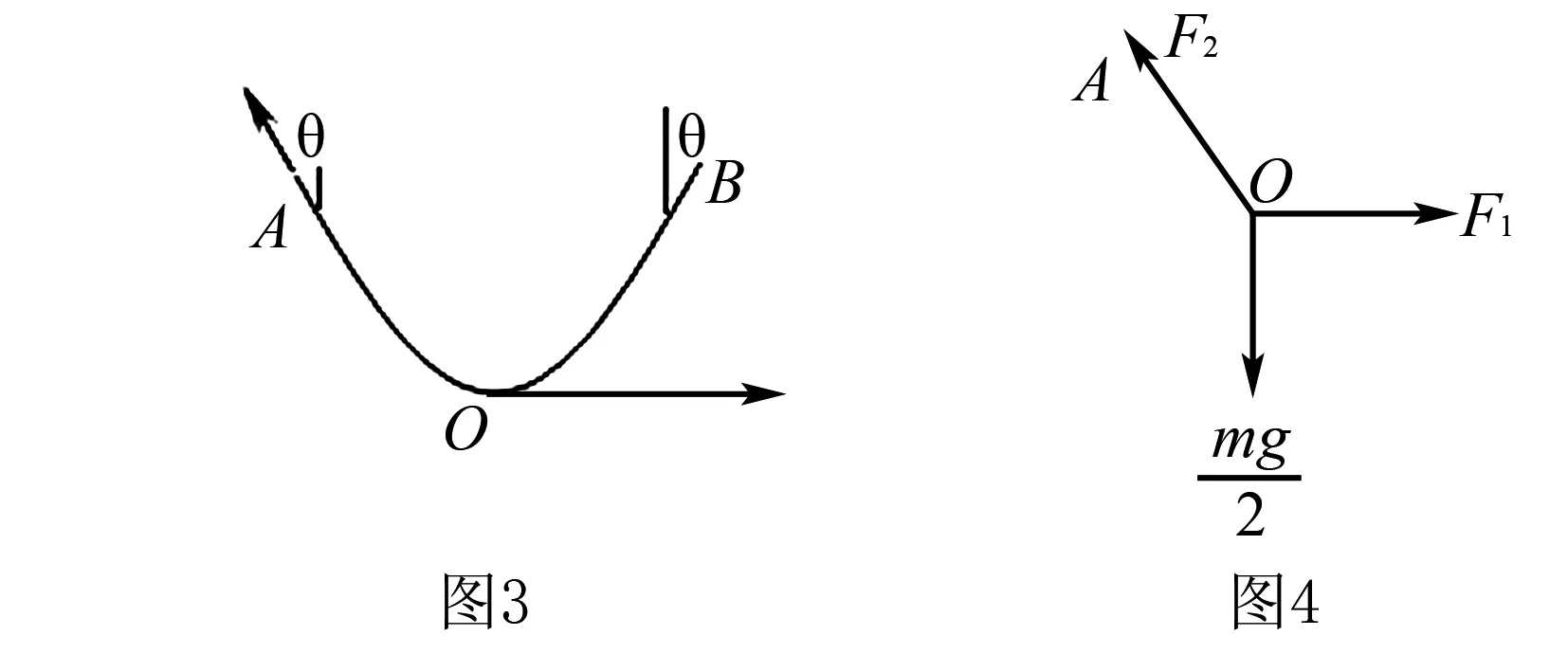

那么除绳端外,绳上其他各点的弹力大小相同吗?
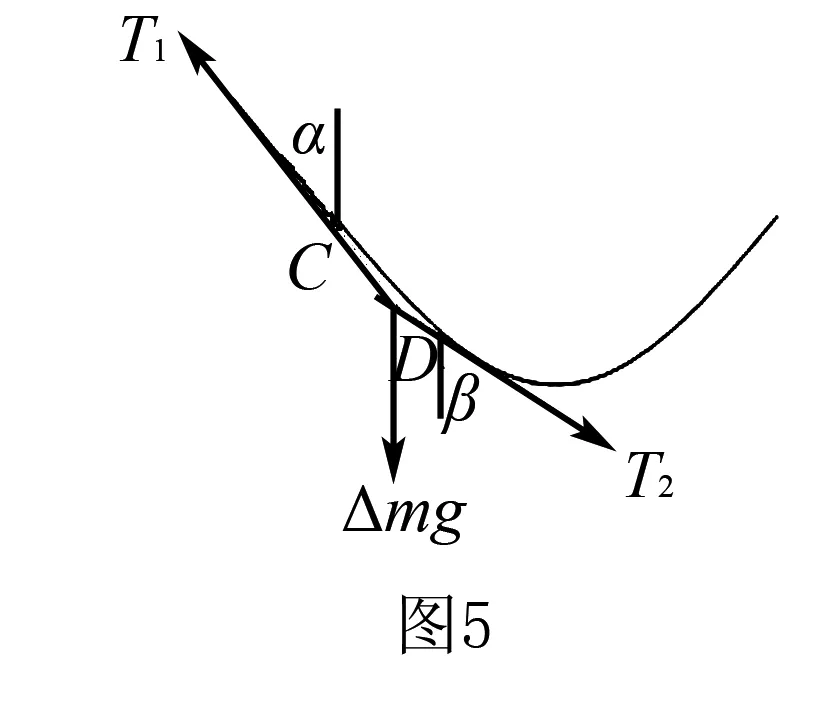
在绳上任意选两点间的一小段绳子作研究对象,如图5所示.设CD间绳的质量为Δm.则CD绳受重力Δmg.
CD两处绳的弹力T1、T2.令T1、T2与竖直方向夹角分别为α.和β.同理可得CD绳受到三个力的平衡图.其中T1.T2方向分别是过绳CD两点的切线方向,由平衡条件有:
T1cosα=Δmg+T2cosβ
③
T1sinα=T2sinβ
④
由③④得:
由于绳子呈曲线,绳CD两点弹力方向与竖直方向夹角α<β.所以T1.>T2.
由此可见:实际绳子具有质量,绳子平衡时不能呈直线,导致绳上各处的弹力大小不同;在什么条件下可以将实际绳子当作“轻绳模型”,由上述分析可知,只有当绳上的弹力远大于绳的重力,且绳子受力时形状呈直线,才能视为“轻绳模型”,例如承载电梯的钢绳,吊车、起重机吊起重物的钢绳,立交桥、斜拉桥及高压电杆上固定电杆的钢索等,都可以视为“轻绳模型”.
基于以上分析,结合共点力平衡知识,不难得出湖南物理卷这道选择题的正确答案应选B.在阅卷中笔者发现平时成绩较好的学生受“轻绳模型”思维定势束缚而错选了C.也有不少学生没有把握恰当的研究对象受力分析导致选错了答案.
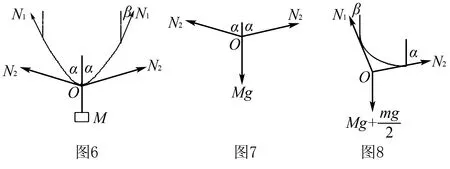
若钉子处绳的弹力为N1.绳中央O点处弹力为N2.如图6所示,先将绳子和物体视为整体分析受力,O点左右两侧绳对O点的拉力N2属于系统内力,则有:
2N1cosβ=(M+m)g
⑤
然后把绳的中点O隔离受力分析,如图7所示,则有:
2N2cosα=Mg
⑥
最后以绳端到中央O处的半段绳子为对象分析受力,如图8所示,则有:
N1sinβ=N2sinα
⑧
由⑤⑥⑦解得:
正确选项为B.
新高考实现从“知识立意、能力立意”向“价值引领、素养导向、能力为重、知识为基”转变,引导考生从“解题”向“解决问题”转变.本题以生活情景素材为载体,通过匠心独运的试题设计,着重考查共点力平衡的基本模型和整体、隔离的思想方法.
三、借题发挥,反思问题
运用物理知识解决实际问题能力的高低,往往取决于学生将情境与知识相联系的水平.以本题为例,学生最容易陷入“轻绳模型” 的定势思维中,认为钉子对绳的弹力大小N1等于绳中央O点处的弹力大小N2,导致选择错误答案C.只有对本题深度探索,巧妙运用整体隔离思想呈现三幅共点力平衡图(如上图6、7、8所示),将实际情境转化成解决问题的物理情境,建立相应的物理模型,才能找到正确答案;而恰当选取研究对象,对对象之间相互作用的观念的深入理解则是正确解决问題的关键所在.
高考物理试题的考查要求,是通过情境与情境活动两类载体来实现的,即通过选取适宜的素材呈现现实中的问题情境,让学生在真实的背景下运用必备知识和关键能力去解决实际问题.基于真实的生活实践情境设置物理问题,是物理命题的一种趋勢,也是物理学科考试体现应用性的重要途径,我们应鼓励并引导学生基于物理学科核心素养解决生活中的实际问题,要从培养物理学科核心素养的视角审视习题教学的目的,通过习题教学,既要发挥以题悟理、用题说法、借题发挥的习题讲评功能,又要启发学生探索问题情境,培养建模意识,使学生在科学思维、探究能力、实践意识、科学态度等方面得到有效提升.因此物理备考复习不仅要关注新科技发展成果,也要关注身边生活实际中的原始物理问题;复习时要注重模型建构能力和推理论证能力的协同发展,要实现从”解题”向”解决问题”的转变,提高学生解决问题的能力.

