高考全国卷求离心率的题型及解法归类
2021-11-24 09:02李定平
数理化解题研究 2021年31期
李定平
(广东省佛山市顺德区罗定邦中学 528300)
圆锥曲线的离心率问题是高考中的一个难点和热点.因为离心率是刻画圆锥曲线形状的一个基本量,能考查考生对圆锥曲线形状最本质的理解,考查数学抽象、数学建模、数学运算等数学核心素养,灵活多变,综合性强.
一、已知焦点三角形中边角关系
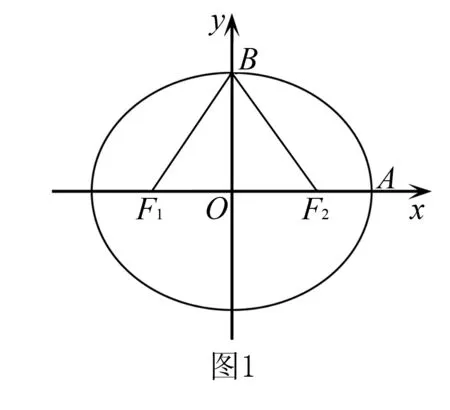

1.已知焦点三角形中的角
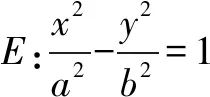
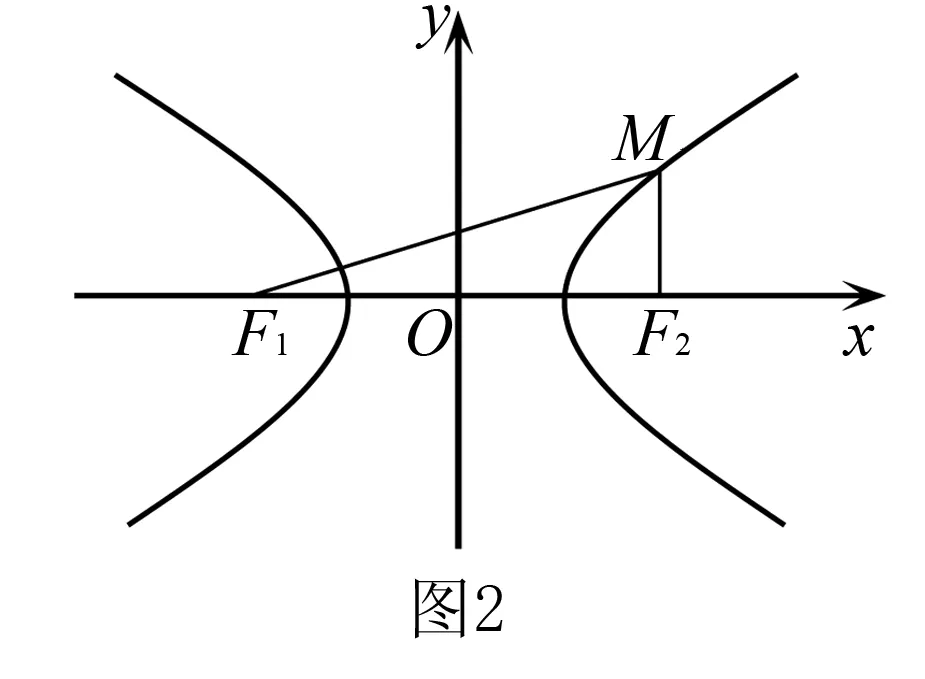


2.已知焦点三角形中边的关系
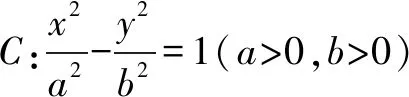
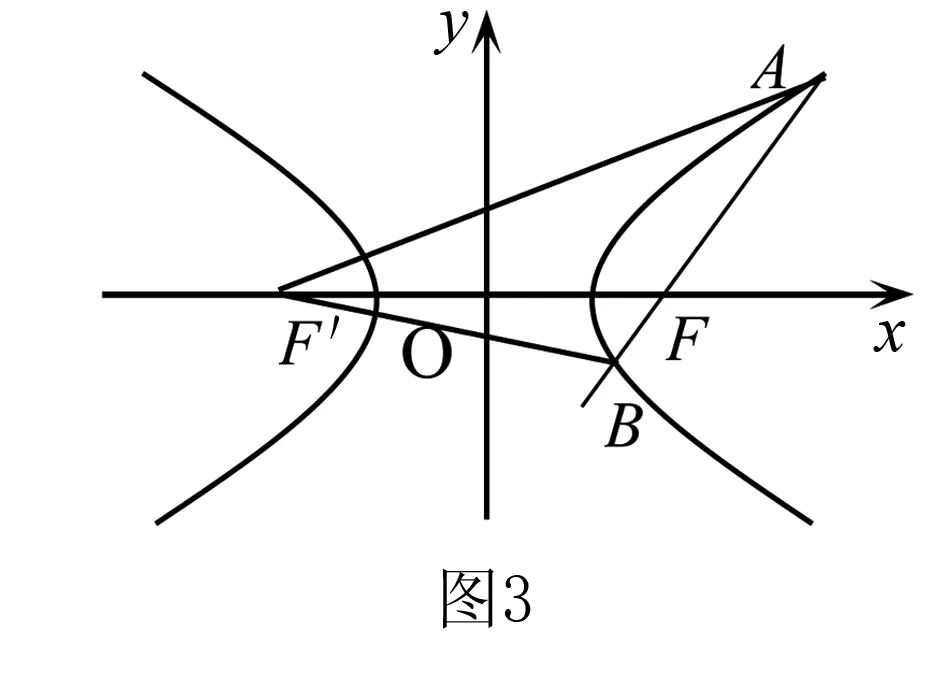
解析1 (几何法)设|BF|=t,则由已知可得|AF|=4t.由双曲线的定义可得|AF′|=2a+4t, |BF′|=2a+t.在△AFF′和△BFF′中,由余弦定理,得(2a+4t)2=(4t)2+(2c)2-2×(4t)×(2c)cos120°,(2a+t)2=(t)2+(2c)2-2×t×(2c)cos60°.即(2a)2- (2c)2=-16at+8ct,(2a)2- (2c)2=-4at-2ct.
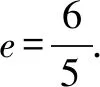
故选A.
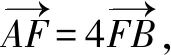

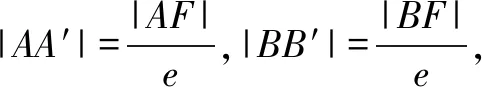

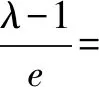
二、由渐近线求离心率
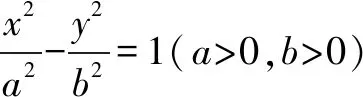
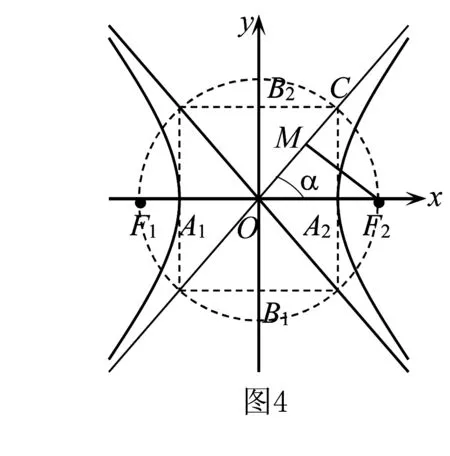

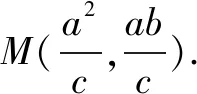
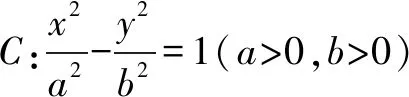
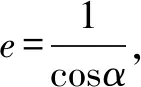
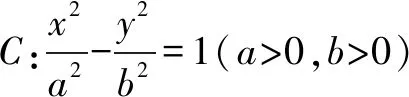

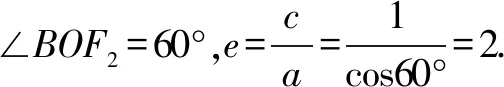
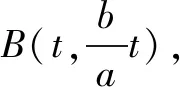
①
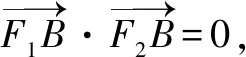
②

三、其它题型
基本思维方法是用坐标法把已知条件化归为a,b,c的关系求离心率.
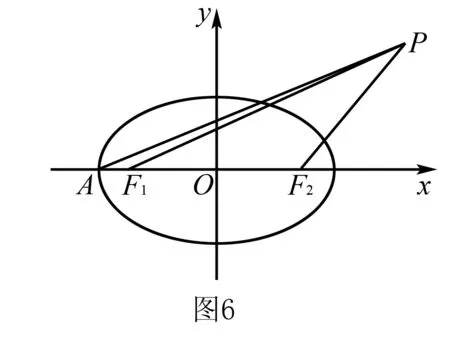
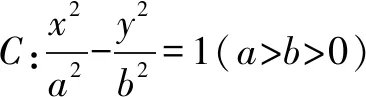
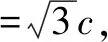




数学是思维的体操,引导学生如何思考才是提升数学核心素养的根本途径.所以把离心率问题归结为一个思考方向(往哪方面想),两条路径(如何达到),三种题型.真可谓“思想方法是王道”.
猜你喜欢
小学生学习指导(中年级)(2022年9期)2022-09-30
中学生数理化(高中版.高二数学)(2022年5期)2022-06-01
中小学校长(2022年1期)2022-03-01
求学·理科版(2022年3期)2022-02-25
小资CHIC!ELEGANCE(2022年1期)2022-01-11
中学生数理化(高中版.高二数学)(2021年5期)2021-07-21
家庭影院技术(2019年7期)2019-08-27
——以《任意角的三角函数》为例
中学数学研究(广东)(2019年4期)2019-04-10
南方周末(2018-03-08)2018-03-08
科学中国人(2017年22期)2018-01-02

