赏析立体几何中的创新问题
焦玉梅
(山东省德州市庆云县第一中学 253700)
立体几何的常规题型只要掌握常规知识点并加以理解,即可求得相关问题.但对于创新问题不仅要掌握相关知识,还要能够较好地对问题进行深入思考,才能破解试题.
一、学科交叉




点评本题与赤道纬度相互结合,考查了空间相关点的坐标表示,意在对学生的空间想象能力和推理论证能力进行检测.
二、实际应用
例2 如图2,水平桌面上放置一个棱长为4的正方体水槽,水面高度恰为正方体棱长的一半,在该正方体侧面CDD1C1上有一个小孔E,点E到CD的距离为3,若该正方体水槽绕CD倾斜(CD始终在桌面上),则当水恰好流出时,侧面CDD1C1与桌面所成角的正切值为( ).

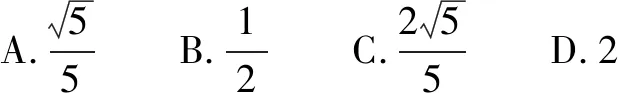
解析由题意知,水的体积为4×4×2=32,如图2.

设正方体水槽绕CD倾斜后,水面分别与棱AA1,BB1,CC1,DD1交于点M,N,P,Q,由题意,知PC=3,水的体积为SBCPN·CD=32.
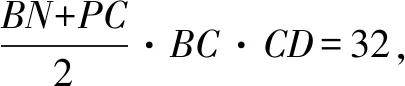
在平面BCC1B1内,过点C1作C1H//NP交BB1于点H,则四边形NPC1H是平行四边形,且NH=PC1=1.
又侧面CDD1C1与桌面所成的角即侧面CDD1C1与水面MNPQ所成的角,即侧面CDD1C1与平面HC1D1所成的角,其平面角为∠HC1C=∠B1HC1.

点评本题以正方形为载体进行考查,解题的关键是建立等式求得BN的值,再将二面角转化到一个直角三角形中即可求解.
三、数列与立体几何交汇
例3斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数:1,1,2,3,5,…为边的正方形拼成长方形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.自然界存在很多斐波那契螺旋线的图案,例如向日葵、鹦鹉螺等.图5为该螺旋线的前一部分,如果用接下来的一段圆弧所对应的扇形作圆锥的侧面,则该圆锥的体积为( ).


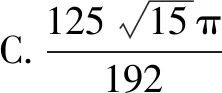
解析根据已知可得所求扇形半径为r=3+5=8,即圆锥母线长为l=8.


点评本题主要根据斐波那契数得圆弧的半径为8,然后根据圆锥侧面展开图计算出圆锥的底面半径和高,从而可得体积.
四、数学文化
例4牙雕套球又称“鬼工球”,取鬼斧神工的意思,制作相当繁复,工艺要求极高.明代曹昭在《格古要论·珍奇·鬼工毬》中写道:“尝有象牙圆毬儿一箇,中直通一窍,内车数重,皆可转动,故谓之鬼工毬”.现有某“鬼工球”,由外及里是两层表面积分别为100πcm2和64πcm2的同心球(球壁的厚度忽略不计),在外球表面上有一点A,在内球表面上有一点B,连接线段AB.若线段AB不穿过小球内部,则线段AB长度的最大值是( ).
解析因为外球的表面积为100πcm2,内球的表面积为64πcm2,所以外球的半径为5cm,内球的半径为4cm.
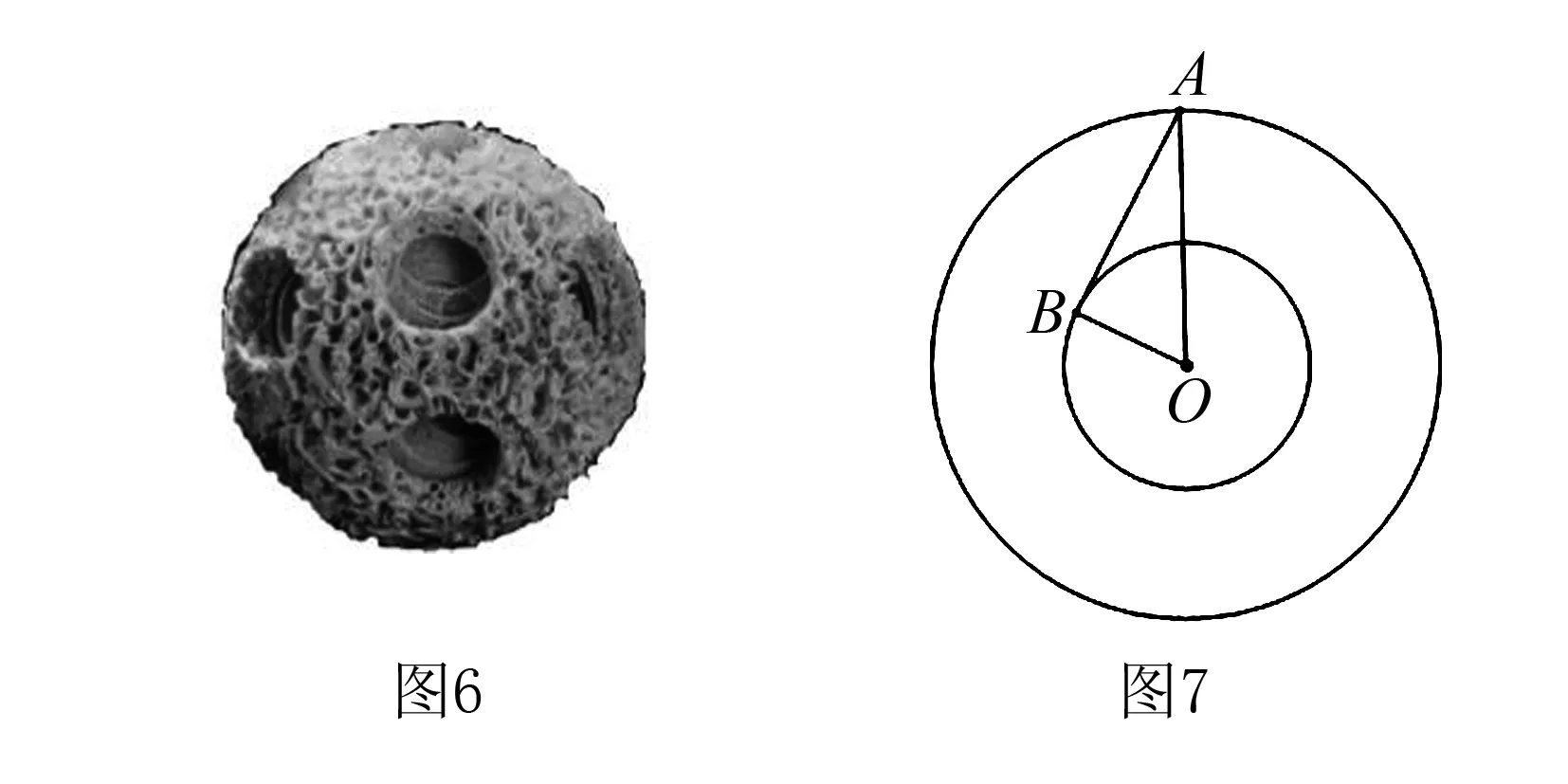
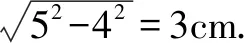
点评本题首先根据题意确定外球的半径以及内球的半径,然后以外球表面上一点A、内球表面上一点B以及球心O作截面,根据线段AB不穿过小球内部得出线段AB与内球相切时线段AB的长度最大,最后通过计算即可得出结果.
五、古代建筑与立体几何

A.正四棱锥的底面边长为6米
B.正四棱锥的底面边长为3米

解析如图8,在正四棱锥S-ABCD中,O为正方形ABCD的中心,H为AB的中点,则SH⊥AB.

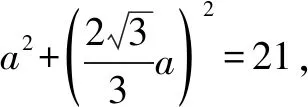
故选AC.
点评利用已知条件画出图象,设O为正方形ABCD的中心,H为AB的中点,设底面边长为2a,利用线面角的定义得出∠SHO=30°,根据已知条件得到各边的长,进而求出正四棱锥的侧面积即可.
六、命题角度创新
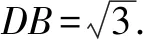
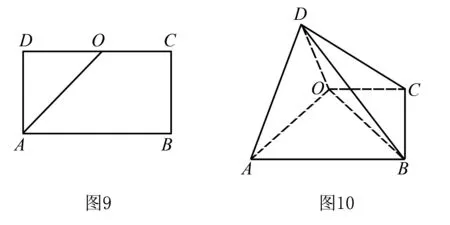
(1)求证:平面AOD⊥平面ABCO;
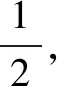
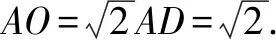
又OB⊂平面ABCO,所以平面AOD⊥平面ABCO.


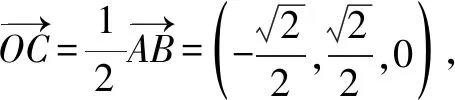


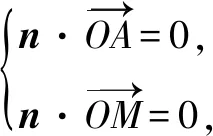

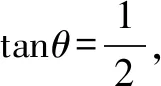

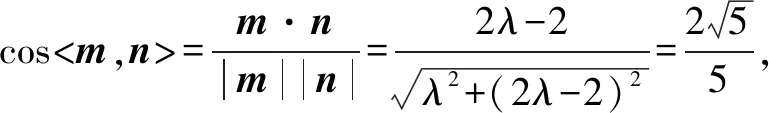
所以M是BD的中点.
点评求二面角的正弦值,可分三步,第一步:求出两个平面的法向量;第二步:求出两个法向量夹角的余弦值;第三步:由二面角范围[0,π]知正弦值为正,由余弦值可得正弦值.本题的命题则拐了一个弯,先由二面角的正切值求得余弦值,从而再确定λ的值.

