艇载振动载荷下固体发动机装药有限元分析①

曲 凯，李金飞，陆巍巍，张旭东

(海军航空大学 岸防兵学院，烟台 264001)

0 引言

固体火箭发动机由于其结构简单、易于维护、可靠性高、推重比大等优点，已广泛应用于各种型号的导弹中。为评估长期服役环境下固体火箭发动机的贮存寿命，必须研究温度、湿度、舰艇振动等因素对发动机贮存寿命的影响。其中，舰艇振动载荷是决定服役环境下固体火箭发动机寿命的一个重要因素。潜射导弹在潜艇中长期经历复杂环境载荷的作用，准确获取固体发动机药柱在全寿命周期中载荷历程，是对其进行技术状态评估的基础。目前，获取发动机药柱载荷历程的方法主要有两种：一是通过安装嵌入式传感器直接测量得到；二是通过测量导弹所承受环境载荷，然后利用有限元仿真软件计算得到。

BUSWELL等[1]和GERHARD等[2-3]采用内嵌式应力和化学传感器来监测固体火箭发动机粘接界面在温度循环、降温时的应力变化和化学老化。研究表明，该应力传感器可以用来研究交变温度应力作用下，复合固体推进剂粘接界面的损伤规律。张守诚等[4]和张波等[5]分别采用壳体外表面和内表面贴片传感器，可有效地测量相应的载荷和脱粘情况，实现发动机局部健康监测。虽然嵌入式传感器已经取得了很大进步，但是到目前为止，该方法还没有大规模运用到实际发动机监测中，所取得的成果还需要进一步通过解剖发动机、取出装药进行试验的方法对其破坏方式进行验证，而且传感器目前大部分只是针对温度载荷产生的应力，对于振动载荷所产生的频率较快的应力测量还没有投入使用。

国内外学者[6-10]针对固体火箭发动机长期贮存、公路运输、载舰值班等情况进行了有限元分析研究，并根据药柱破坏判据对其的可靠性进行了判断，为发动机寿命评估提供了一定依据。但是，仿真计算过程中振动载荷输入条件都为低频振动载荷，特别是舰船运动周期为10 s，没有将实测振动数据作为输入条件进行仿真计算。王永帅等[11]针对舰载立式贮存固体发动机药柱和粘接界面的蠕变损伤分别展开了研究。王鑫等[12]开展了发动机固化降温、长期重力和低频振动联合作用下的有限元计算，得到了药柱应力应变分布规律。文献[6,8]研究表明，虽然舰船摇摆运动所产生的加速度载荷比较小，达不到固体火箭发动机装药破坏的极限载荷，但是这种小应力载荷的长期作用也可能产生较大损伤。因为推进剂药柱在构成上是多组分混聚物，主要由高分子聚合物基体和掺入其中的大量固体氧化剂颗粒及金属燃料颗粒组成。由于固体颗粒在基体中是一种机械混合，在外界各种小应力载荷作用下，推进剂内部将发生不可逆的损伤。从细观层面上讲，该损伤包括基体结构的断裂以及颗粒与基体界面的“脱湿”，而且这些细观损伤可能会聚合和汇集成宏观裂纹、脱粘等缺陷[13-14]。

综上所述，本文利用粘弹性有限元分析方法计算艇载固体发动机在实测振动载荷作用下的应力应变场，通过分析确定发动机装药比较容易出现问题的部位，并计算研究危险部位Mises应力和剪切应力随时间变化曲线，最后通过雨流计数法获取发动机装药危险部位的疲劳载荷特性，可为后续开展装药实验室加速老化试验和艇载固体发动机寿命评估奠定基础。

1 振动载荷作用下装药结构有限元分析

1.1 三维实体建模

对某型艇载导弹固体火箭发动机进行三维有限元分析，首先必须建立其相应三维结构模型。本文所研究的固体火箭发动机由金属壳体、绝热层、衬层、翼柱形推进剂、人工脱粘层等部分组成，如图1所示。

图1 某型导弹发动机结构示意图

论文研究重点是分析发动机装药危险部位的应力应变分布，为提高运算效率，对发动机刚性壳体结构进行一些必要简化。根据某型导弹固体发动机的结构特点，忽略对应力分析不产生明显影响的复杂结构，比如发动机壳体的前裙、后裙和点火器等结构，利用建立有限元仿真软件的模型构建模块建立发动机模型，如图2所示。

图2 某型导弹发动机三维模型示意图

为更清楚地观察所建固体火箭发动机模型的内部结构，现在取该发动机三维模型的1/2进行分析。由图3可见，发动机内部结构相对比较复杂，它由头部和尾部开槽的翼柱形推进剂药柱、人工脱粘、衬层和发动机壳体组成。该发动机为了减少应力集中，在药柱头部和尾部均设有人工脱粘绝热层，用来消除头部和尾部的应力集中。

图3 某型导弹发动机1/2建模结构示意图

1.2 固体火箭发动机材料参数的选取

进行有限元分析，还需要提供所建模型材料的基本性能参数。其中，该型发动机药柱的弹性模量通过开展发动机所使用的推进剂松弛模量测量实验得到。该固体火箭发动机的装药、壳体、衬层材料参数见表1。

表1 材料性能参数

由于这里推进剂装药采用线性粘弹材料，有限元分析软件为了建立本构关系，在计算过程中需要用到体积模量函数K(t)和剪切模量函数G(t)，其计算公式按照式(1)和式(2)计算。

(1)

(2)

通过推进剂应力松弛试验[15]，可获得装药的应力松弛模量函数Prony级数形式为

(3)

式中Ee为平衡模量；τi为松弛时间。

瞬态模量E0可由下式计算：

(4)

根据应力松弛试验原理，n、t和τi可以任意选取。这里n取4，t取1、4、40、400 s和600 s，τi取0.05、0.5、5和50。因此，测量推进剂装药在各时间点上的松弛模量数据，如表2所示。

表2 推进剂松弛模量数据

根据上述条件，式(4)里面有五个未知数，分别为Ee、E1、E2、E3和E4。将表2中的试验数据代入到式(4)中，可得到5个方程，因此可将5个未知数求出。最终得到松弛模量函数曲线，如图4所示，方程如式(5)所示。

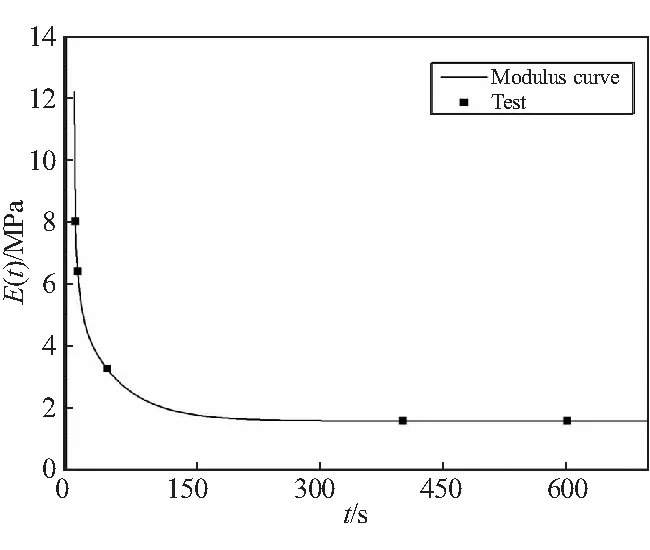
图4 推进剂装药松弛模量曲线

E(t)=1.561+1.685e-t/0.05+2.167e-t/0.5+

3.034e-t/5+3.731e-t/50

(5)

1.3 载荷施加与边界条件

由于进行有限元计算所需的边界条件和载荷条件与选取的固体火箭发动机参考坐标系相关，因此首先确定有限元分析的参考坐标系。为建模研究方便，本文采用的坐标系与潜艇航行坐标系相同，如图5所示。

图5 固体发动机坐标系示意图

不论选取何种坐标系，在进行有限元分析时，任何微元的受力可分为体积力和表面力。有限元分析中每个微元所受到的应力大小仅取决于微元形变的大小，与所选取的坐标系无关，因为无论在惯性坐标性下还是非惯性坐标系下其物体发生形变量是相同的。微元所承受体积力与坐标系的选取密切相关，因为在不同的坐标系中微元运动规律不同，产生的加速度体积力也不相同，而且在有限元分析中，体积力不是未知要求解的载荷，而是作为已知载荷条件输入到模型当中。

1.3.1 边界条件

由于某艇载导弹固体火箭发动机装载于潜艇的发射筒中，如图5所示。为防止发动机在发射筒中左右、前后移动，发动机壳体与发射筒内壁之间装有适配器。除此之外，为防止发动上下移动，在发动机圆筒段与发射筒内壁之间还装限位剪切装置。因此，发动机壳体圆筒段可以近似认为位移为0，即

ui=0(i=r,z,θ)

(6)

由于发动机前后封头与发射筒之间没有物理连接，因此可视为自由表面。

发动机装药内孔，在未点燃燃烧时，其与空气的接触边界为自由表面。

综上所述，选取的发动机坐标系建立装药有限元分析模型时，施加的边界条件为

(1)发动机壳体圆筒段为固定边界条件；

(2)发动机前后封头、装药内孔表面为自由边界条件。

1.3.2 载荷条件

发动机装药内孔，在发动机未点火时，径向所受外力为零，即

σr=0

(7)

由于在潜艇运动过程中，固体火箭发动机装药变形量相对于发动机的位移运动非常小，可以忽略其影响。因此，可假定发动机装药和发动机壳体的位移运动规律相同。

根据达朗贝尔原理，可求解发动机装药微元在惯性坐标下的体积力，计算公式如下：

(8)

其具体数值由实测潜艇发射筒中固体火箭发动机的振动数据确定，根据文献[16]研究表明，发动机所遭受的振动载荷主要集中在振动幅值比较小的区域内，而且通过对载荷频谱分析表明，10 s载荷的频谱与1000 s振动载荷的频谱基本一致。考虑到振动载荷频率快，载荷步比较小，计算量较大，所以综合考虑上述因素，以10 s为时间单位作为载荷输入，如图6所示。

(a) X axis acceleration-time curve

1.4 网格划分

根据有限元分析步骤，还需要对所建立三维实体模型进行网格划分，采用自由四面体划分方式，划分单元总数为967 888个，为了更好说明发动机各个组成部分的网格划分情况，选取其网格的1/2进行展示，如图7所示。

图7 某型导弹发动机三维模型网格划分图

完成上述步骤后，就可以利用有限元计算软件对固体发动机在振动载荷下进行应力应变分析。

1.5 计算结果

利用有限元计算软件进行显式动力学分析，仿真计算机采用8个CPU处理器(每个处理器主频2.33 GHz)，内存24 GB，计算的载荷步为10 000步，步长时间为0.01 s，得到了艇载导弹发动机药柱在执行战备值班任务时遭受典型振动载荷0～10 s的应力应变分布。图8～图11分别为4.8 s时刻发动机装药Mises应力场、最大主应变场、τyz剪应力场和γvz剪应变场。

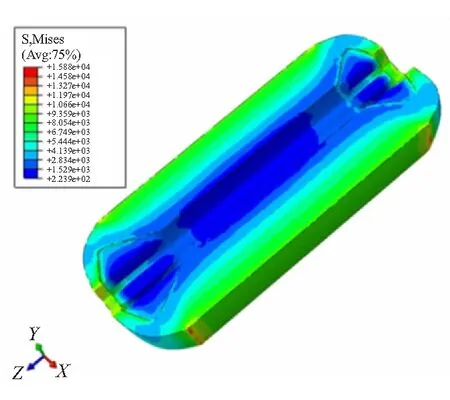
图8 4.8 s药柱Mises应力云图

图9 4.8 s药柱最大主应变云图

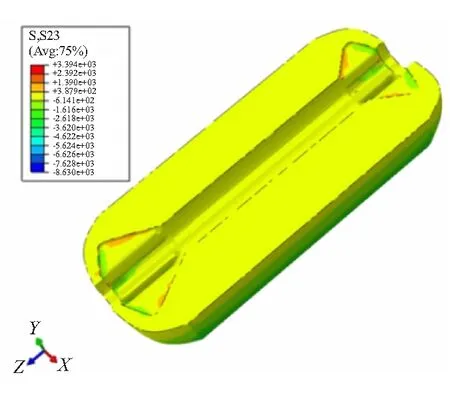
图10 4.8 s药柱yoz平面剪应力云图

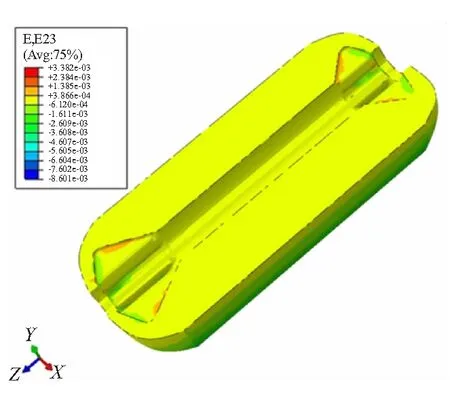
图11 4.8 s药柱yoz平面剪应变云图

根据计算结果可知，在4.8 s时，装药的Mises应力最大值为15.88 kPa，其主应变最大值为4.599×10-3，yoz平面剪应力最大值为3.394 kPa，yoz平面剪应变最大值为3.382×10-3。其中，Mises应力和最大剪应变位置分别位于发动机药柱头部尾部外表面，而yoz平面剪应力和剪应变位置位于发动机药柱内表面上，而且它们都远远低于材料相应的极限破坏值。因此，推进剂装药不可能由于瞬时受力超过极限临界值而发生破坏。但这种振动载荷对艇载固体发动机装药结构可能发生累积损伤，而且其破坏形式主要包括以下两方面：

(1)拉伸、压缩的交变应力循环会对药柱造成机械损伤，降低药柱力学性能；

(2)另外，振动产生的惯性力会在固体发动机药柱粘接界面产生交变的剪切应力，降低粘接界面剪切强度，从而造成粘接界面的破坏。

2 艇载固体发动机装药危险部位的确定

2.1 发动机装药应力分布

危险部位可按照装药的破坏形式来确定，关注Mises应力和yoz平面界面最大剪切应力较大的部位。首先定义两条路径和一个截面A-A。两条路径分别为用红“▲”点和红“■”点来表示，并命名为路径1、路径2，如图12(a)所示。路径1和路径2分别位于发动机外表面和内表面，并贯通整个装药的轴向。发动机截面A-A靠近发动机尾部，该位置为发动机4.8 s时内孔应力最大的截面。选取的路径3为发动机截面A-A中红点沿顺时针沿装药内孔行进，并绕内孔一周最终回到该点的路径，如图12(b)所示。

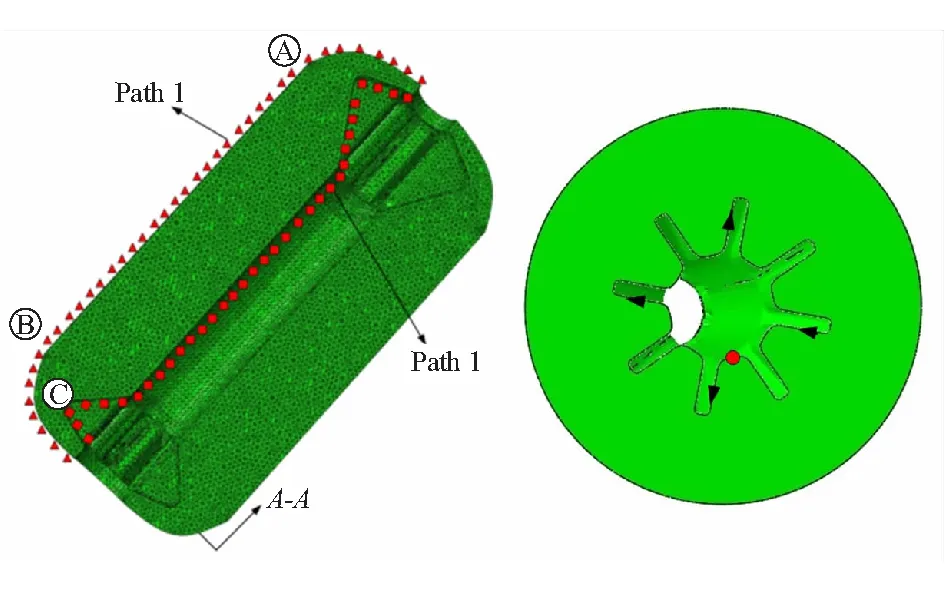
(a) Paths of 1/2 grain (b) Section A-A

2.2 根据Mises应力确定危险点

为了研究4.8 s时发动机的Mises等效应力分布规律，首先研究发动机装药沿各个路径上各点的应力分布情况，因为最大应力部位会出现在这些路径上。每条路径上Mises应力分布，见图13。

(a)Mises stress of path 1

由图13(a)、(b)可见，在发动机头部A点和尾部B点、C点Mises等效应力较大，其都没有位于装药的两端，而位于翼槽和人工脱粘层后面，曲线中间呈现明显双峰特点。这是由于头部和尾部人工脱粘设计释放了这两个部位的应力集中。由图13(c)可见，在装药内孔表面上，应力最大部位均在翼柱形药柱的8个星角处，而且位于发动机装药下部翼柱的星角应力较大，考虑对称性，取C点作为装药星角易发生破坏部位。

根据上述分析，取Mises等效应力较大的点A、B、C作为发动机装药易于破坏位置来重点研究。

2.3 根据粘界面最大剪切应力确定危险点

研究4.8 s时发动机粘接界面的最大剪切等效应力分布场规律，确定沿发动机装药沿路径1和路径2的剪应力分布情况,如图14所示。可见，在发动机头部的A点、发动机尾部的B点和C点等局部点的界面剪切等效应力较大。

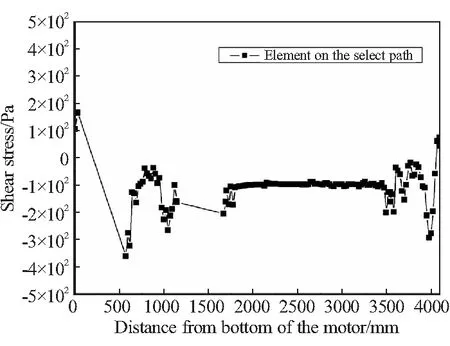
(a)Shear stress of path 1

综合考虑装药最大等效应力和粘接界面最大剪切应力两个方面，确定发动机装药容易发生破坏的危险点为A点、B点和C点。计算过程中，记录这些危险点每一个载荷步的应力应变数值。

2.4 危险部位的应力曲线

根据所得仿真计算结果和所确定的发动机装药危险部位，研究A点、B点和C点的Mises等效应力随时间变化的规律，如图15所示。同时，研究粘接界面A点、B点和C点的最大剪应力随时间变化的规律，如图16所示。

(a) A point (b) B point (c) C point

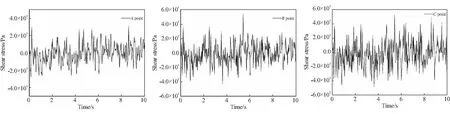
(a) A point (b) B point (c) C point

通过观察图15可知，危险点A的Mises应力幅值最大，而C点的Mises应力幅值最小。另外，每一个危险点的Mises应力加载周期差别不大。通过观察图16可知,危险点C的剪应力幅值最大，而A点的剪应力幅值最小，但其最大值小于对应的Mises等效应力。不论是Mises等效应力还是剪应力，都远低于推进剂及相应粘接界面的载荷破坏极限。因此，推进剂装药不可能由于瞬时受力超过极限临界值而发生破坏。虽然，长期振动载荷引起的载荷较小，但是其作用时间长，其疲劳损伤累积效应予以关注。

3 发动机装药危险部位疲劳载荷特性分析

为后续研究振动载荷引起的疲劳累积损伤，需要对发动机装药进行疲劳损伤试验研究。因此，首先需要对危险点A和危险点C分别研究其Mises等效应力和剪应力的疲劳载荷特性，才能设计合理的装药结构件损伤试验，为后续发动机疲劳损伤评估奠定基础。

在各种疲劳特性分析方法中雨流计数法[17-18]由于其原理与材料疲劳损伤机理相一致，而被广泛使用。利用雨流计数法，对危险点A的Mises等效应力载荷特性的分析结果，如图17所示。把循环加载Mises应力幅值按照1000 Pa为一个等级，对其进行计数统计，结果如图18所示。

图17 发动机A点雨流计数结果曲线

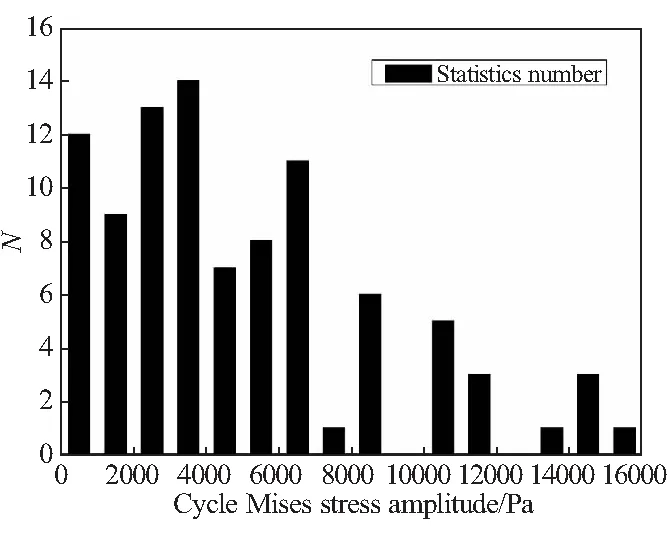
图18 发动机A点Mises循环应力幅值分布曲线

由图17可见，在0～10 s范围内，发动机危险点A累计作用94个Mises应力循环，其中最大循环应力幅值为15.573 kPa，最大循环平均应力为8.891 kPa。由图18中可见，危险点A点Mises应力循环大多数集中在小应力幅值对应区域，比如小于循环应力幅值低于7 kPa的个数为73个，占对应应力循环总数的77.7%，随着加载循环应力幅值的持续上升，循环的数量不断减少。为了方便说明把Mises循环应力幅值低于7 kPa定义为小应力加载循环。

利用雨流计数法，对危险点C的剪应力载荷特性的分析结果，如图19所示。把循环加载剪应力幅值按照1000 Pa为一个等级，对其进行计数统计，结果如图20所示。

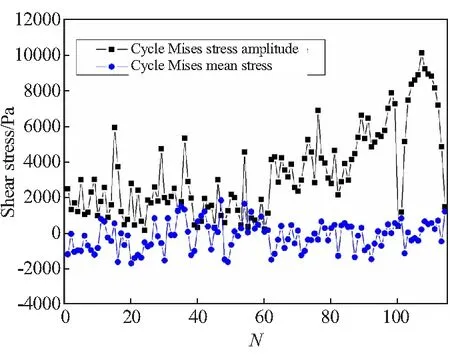
图19 发动机C点雨流计数结果曲线

图20 发动机C点循环剪应力幅值分布曲线

由图19可见，在0～10 s范围，内发动机危险点C累计作用114个剪应力循环，其中最大循环应力幅值为10.11 kPa，最大循环平均剪应力为1.8 kPa，并在0点附近振荡，远低于危险点A的最大循环平均剪应力。从图20中可以看出，危险点A点平均剪应力循环大多数也集中在小应力幅值对应区域，比如小于循环应力幅值低于6 kPa的个数为102个，占对应应力循环总数的89.5%，随着加载循环应力幅值的持续上升，循环的数量不断减少。为了方便说明，把剪切循环应力幅值低于6 kPa定义为小应力加载循环。

4 结论

对某艇载固体火箭发动机翼柱型装药战备值班期间振动环境载荷作用下的应力应变情况进行了有限元模拟，并对装药危险部位的疲劳载荷特性进行了分析，研究结果表明：

(1)该发动机翼柱型装药在振动载荷作用下产生的应力应变远远小于其破坏极限，不会发生突然断裂破坏。

(2)长期振动载荷作用下应力呈现随机性变化，确定固体发动机头部外表面A点遭受的Mises应力最大，药柱后翼槽危险点C的剪应力幅值最大。

(3)根据雨流计数法，危险点Mises等效应力循环加载幅值大于剪应力循环加载幅值，而且Mises等效应力循环加载均值明显大于剪应力循环加载均值。

(4)不论是Mises应力还是剪应力，循环大多数集中在小应力幅值(Mises应力幅值低于7 kPa，剪切应力幅值低于6 kPa)对应区域，A点Mises应力和C点剪应力的小应力循环数分别占对应应力循环总数的77.7%和89.5%。