一种求解命题公式骨干集的警示传播算法*

王 帅，王晓峰，梁 田，李 志

(北方民族大学计算机科学与工程学院，宁夏 银川 750021)

1 引言

骨干集一词是在布尔可满足性SAT(SATisfiability)问题相变研究中提出的[1 - 6]，一个可满足命题公式的骨干集文字必将会出现在所有满足指派中[7 - 10]，它对命题公式的可满足性判定难度有重要影响[11 - 17]。骨干集越大，公式的判定难度越大。如果给定一个命题公式的骨干集，那么公式的判定将会变得容易。然而，一般情况下，求解命题公式的骨干集是困难的。目前，学术界主要使用以下几种算法求解骨干集，最为基础的是Marques-Silva等人[18]利用骨干文字位于所有的满足指派中的性质，使用minisat求解器求出所有满足指派，并使之相交得到骨干集。Janota等人[19]通过对文献[18]方法的改进，提出一种更少迭代次数的骨干集求解算法，同时利用骨干文字反向赋值会使公式不满足的性质，提出一种文字翻转技术求解骨干集。Previti等人[20]利用抽象论证中理想语义和骨干集的联系，设计一种新的主干网络并利用带有偏好的SAT求解器求解骨干集。Guo等人[21]以一次测试算法为基础，运用启发式思维设计出一种评分机制与过滤机制相结合的骨干集算法。de Haan等人[22]利用结构化实例中的局部骨干文字很大一部分都是全局骨干文字的特点，以局部计算的复杂度来判断局部子句的骨干文字，进而求解骨干集。Zhu等人[23]利用集成电路中的错误空间和时间定位复杂化，设计了一个基于该技术的SAT求解方法，求解大规模公式中的骨干集。Ivrii等人[24]利用权重与数值等启发式信息，在逻辑上假设骨干文字用以加快算法的搜索速度。Kilby等人[8,25]在求解后门集时也对骨干集进行了求解，对比2个集合发现后门集与骨干文字之间几乎没有交集，通过对后门集赋值化简公式求解骨干集。上述方法都具有一定的局限性。

信息传播算法是基于因子图模型的一种信息迭代算法，已有的实验结果和理论结果表明：信息传播算法求解SAT问题效果较好，特别是对于因子图为树形结构的公式，算法能够在多项式时间内给出问题的有效解。警示传播WP(Warning Propagation)算法是信息传播算法的一种最基本形态，其特点是基于信息传播可以以高概率确定一个可满足指派部分变元的取值，从而化简公式。WP算法的基本思想是：在信息迭代过程中，根据当前子句的可满足性对变元取值的依赖程度(概率)，“冻结”部分变元的取值。同时，在计算出子句中变元的取值倾向(概率表示)后，在子句与变元之间进行信息传递，使信息传递的值以较大概率决定变元的真值指派满足给定公式。子句c与变元i之间这种传递取值倾向的概率为1时，表示子句c的可满足性完全依赖于变元i的取值。对信息传播算法的原理分析中发现，当算法收敛时，高概率冻结部分变元的赋值，可以对命题公式进行化简。表明WP算法所“冻结”的变元，高概率是骨干集中的变元，因此本文设计一种求解命题公式骨干集的WP算法。

2 基础知识

设子句集合F={a,b,…,}为一个具有m条子句的CNF公式，其中子句a中含有n个变量x1,…,xn。F可以用因子图(Factor Graph)表示，因子图可视为二分图，图中的节点可分为2类：一类是文字节点；另一类是子句节点。其中:

μa→i()表示子句a对文字xi的取值倾向;

V(i)表示包含文字xi的子句节点集合;

V(a)表示包含于子句a中的文字节点集合;

骨干文字：如果F={a1,…,am}是一个可满足的公式，一个文字xi出现在所有的满足指派中，那么文字xi就是骨干文字。

骨干集：文字的集合，指对于一个可满足命题公式的每一个真值指派使得骨干集中的文字均为真。

2.1 警示传播算法的基础定义符号

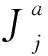
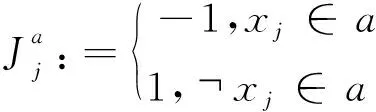
(1)

(2)

(3)

其中，V-(j)表示变元xj负出现的子句集合。V+(j)表示变元xj正出现的子句集合。V(j)a表示变元xj出现的子句集合去除子句a。

显然，

(4)

2.2 警示传播算法的基本思想

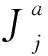
μα→i(t+1)=

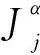
(5)

可化简为式(6)所示：

(6)

其中，断定函数如式(7)所示：

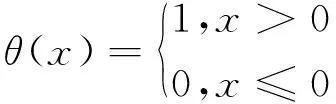
(7)

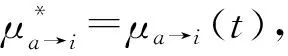
3 求解命题公式骨干集的警示传播算法

(8)

(9)

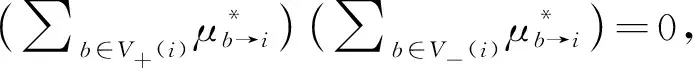
(10)

所以式(10)对应于：

(11)

即ci=0时，通过Hi可以高概率地为文字xi赋值。当Hi≠0时，文字xi高概率地为骨干文字。

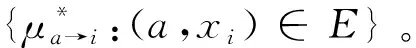
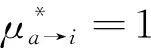
因此，本文设计骨干集求解算法，首先增加预处理过程，取消初始时刻对全部变量的随机赋值，改为对特定子句和变量赋值化简后再进行随机赋值。其次利用WP算法的特性确定部分骨干文字，由于在化简求解的过程中容易出现部分文字的Hi=0的情况，需要设计一个文字消除方法，消除特定Hi=0的文字，化简整个公式，从而快速求解出骨干集。通过对WP算法过程的分析发现，子句会向文字传递趋向值，不同取值倾向子句个数相同，该文字就是需要消除的特定文字即非骨干文字。可知在求解命题公式骨干集的问题时，Hi不为0的文字是骨干文字，对文字进行赋值并对公式进行化简，可以得到新的公式和骨干文字，反复迭代直到不收敛，即可得到一组通过Hi获得的骨干文字。因此，去除式(11)中对xi的随机赋值，确定所有的xi赋值，并对图进行化简进行下一轮计算。本文算法设计如算法3所示。

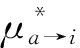
输入:CNF公式F的因子图，最大迭代步数tmax。

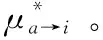
1. 对因子图的单位子句赋值；

2. 将剩下的每条边进行随机赋值；

3.fort=1 totmax

4. 调用算法2更新(μa→i(t-1)→μa→i(t))；

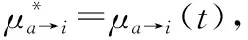
6.endfor

7. 输出结果。

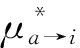
输入:警示信息μb→j:b∈V(j)a,xj∈V(a)xi。

输出:新的μa→i。

1. 当V(a)xi=∅，输出μa→i=1；

2.forj∈V(a)xi

3.ifV(j)a=∅

4.Hj→a=0；

5.else

6.hj→a=(∑b∈V+(j)aμb→j)-(∑b∈V-(j)aμb→j)；

7.endif

8.endfor

算法3求解命题公式骨干集的警示传播算法

输入:命题公式，最大迭代次数iter。

输出:状态标识，骨干集。

1.for迭代次数t=1 toiter

3.if本文WP算法不收敛

4. 退出；

5.else

6. 计算所有Hi和冲突标识ci;

7.WhileHi≠0do

8. 当Hi>0时，令xi=1;

9.当Hi<0时，令xi=0;

10.消除Hi=0中趋向值个数相等的文字，进行图化简;

11.endwhile

12.endif

13.endfor

14.输出赋值结果，即骨干集。

4 实验与结果分析

实验主要从3个方面进行对比分析：(1)使用WP算法在不同类型的实例集上进行收敛性测试，分析算法的可行性。(2)在相同的实例集上与一次迭代算法Iterative SAT Testing(iter)[18]、核心文字翻转算法Core-based Algorithm(core)[19]和局部骨干算法Iterative Local Backbones(lb)[22]等经典算法对比分析算法的求解时间。(3)在相同的实例集上对比近几年常用的核心翻转算法[19]和评分过滤算法[21]，分析算法的收敛性和准确度。

4.1 算法的可行性

为了测试算法的可行性，使用不同类型的实例集进行收敛性测试，只有收敛的实例才可通过WP算法进行骨干集的求解。选取了实际生产中常见的树形因子图、正则3.4Sat和随机Sat这几种结构不同的测试集。使用算法1对不同的实例进行收敛性测试，结果如图1所示。

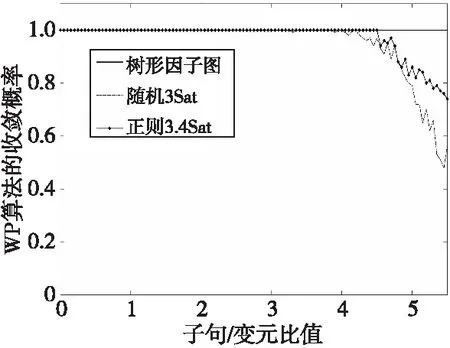
Figure 1 Convergence of different instances图1 不同实例的收敛性

通过图1可知，本文WP算法在树形因子图的实例集上必定收敛，在随机Sat和正则3.4Sat上当子句/变元比值小于3.5时也必定收敛、大于3.5的部分也具有较好的收敛性。因此，实验结果表明，本文WP算法在绝大部分实际生产问题中都具有较好的收敛效果。证明了本文WP算法对骨干集求解的可行性。

4.2 与经典算法的时间对比

分析了算法的可行性后，算法的运行时间往往也是求解命题公式骨干集的关键。本文构建了n=200,400,600的树形因子图和随机Sat因子图进行对比实验。用本文WP算法和其它经典的骨干集算法对相同类型的因子图的多个实例进行求解，对比不同算法求解时间，结果如图2～图4所示。

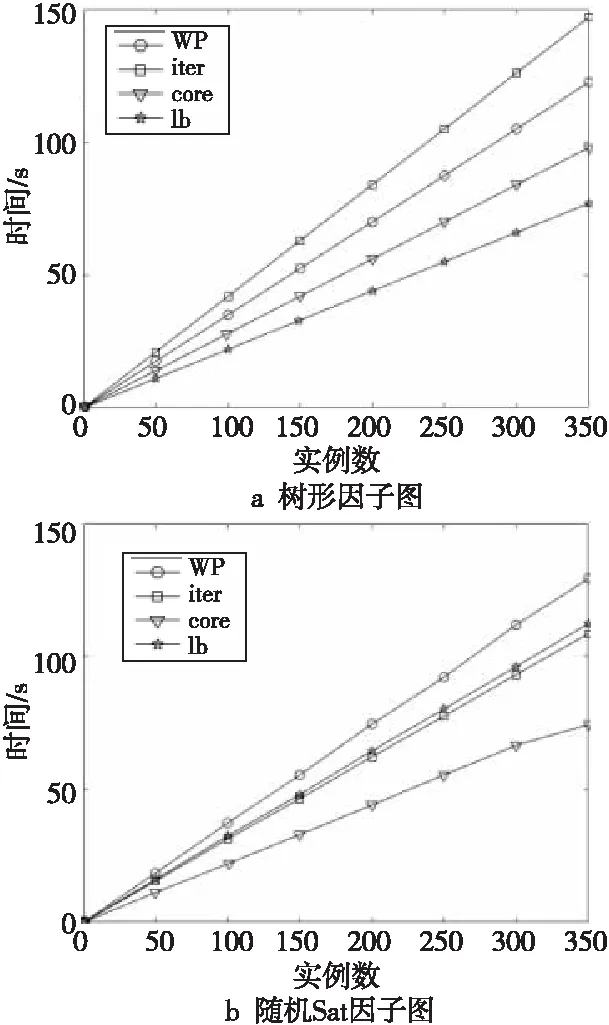
Figure 2 Solution time of each algorithm with n=200图2 n=200时各算法的求解时间

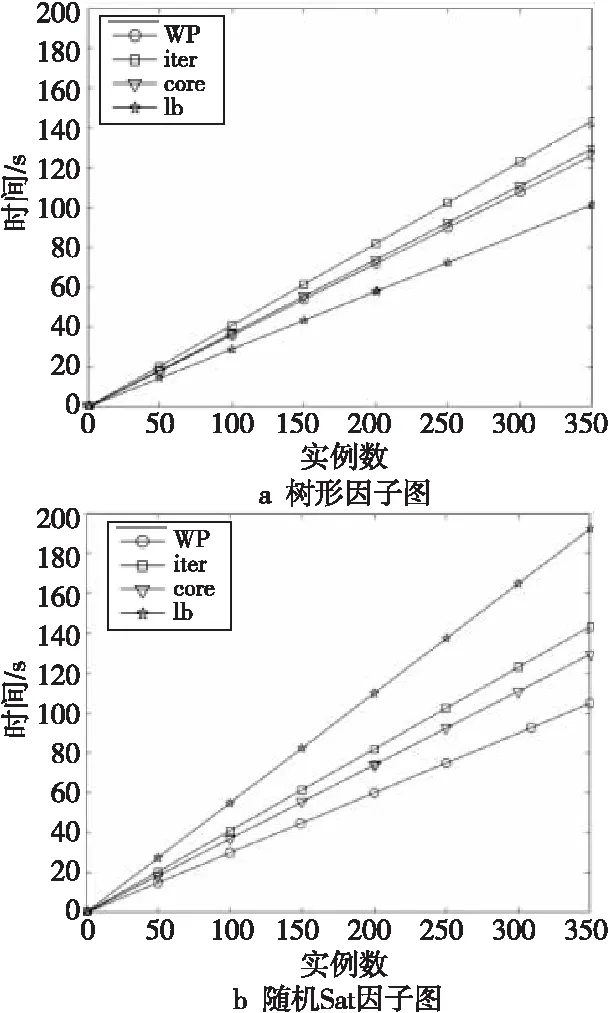
Figure 3 Solution time of each algorithm with n=400图3 n=400时各算法的求解时间

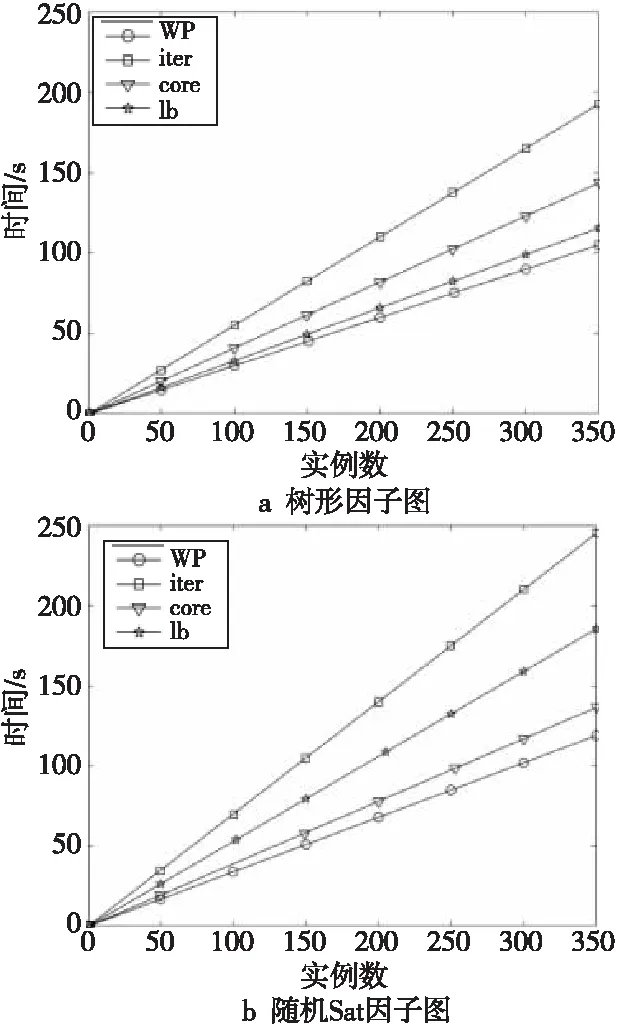
Figure 4 Solution time of each algorithm with n=600图4 n=600时各算法的求解时间

Figure 5 Time comparison on fla problem of three algorithms图5 3种算法在fla问题上的时间对比

通过图2～图4可知，随着变元数目的不断增加，本文WP算法明显优于经典的骨干集求解算法。在本实验中，发现当变元数目在400～600时，本文WP算法和lb算法的求解时间有优势，而且随着变元数目增多，其时间优势逐渐增大。而且本文WP算法相较于lb这类近似算法，在求解随机Sat问题上具有一定的时间优势，但在结构性实例上优势不明显。同时实验发现随着变元的增多，本文WP算法的求解时间呈线性增长，相对于经典算法的求解时间的增长几乎可以忽略不计。即可理解为本文WP算法在求解变元数目较多的实例上相对于经典算法具有非常明显的优势。

4.3 与目前常用算法的时间对比

在求解骨干集的算法中，大部分都是进行局部求解，然后根据局部解推测出全局解。目前最为常用的骨干集算法是Janota等人[19]提出的文字翻转算法和Guo等人[21]设计的启发式评分过滤算法。在相同实例下对比2种算法与本文WP算法的求解效果，结果如图5所示。

从图5中可以发现，本文WP算法在求解命题公式骨干集时，随着问题复杂性的增大，求解时间优于另外2种算法。

5 结束语

本文通过对WP算法的修改，设计一种求解命题公式骨干集的警示传播算法，该算法在构建的特殊命题公式上求解的速度都较快，在SAT-encoded “Flat” Graph Colouring Problems(fla)基准集上求解速度比构建的特殊命题公式慢。但是，与文字翻转算法和启发式评分过滤算法相比还是有所提高的。

在后期的工作中，考虑通过使用弱后门集与骨干集没有交集的理论，对WP算法进行改进，使其能求解出更多的骨干文字。