PMLSM动子位置估算与校正策略研究*
党存禄, 陈文德
(1.兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050;2.兰州理工大学 甘肃省工业过程先进控制重点实验室,甘肃 兰州 730050;3.兰州理工大学 电气与控制工程国家级实验教学示范中心,甘肃 兰州 730050)
0 引 言
永磁直线同步电机(PMLSM)因为其独特的物理结构,不需要中间转换结构就能将电能转化为使电机做直线运动的机械能,实现了无需任何传动机构的“零传动”,克服了由中间转换结构带来的不利因素,因此在一些精密加工、仪器仪表业、电子装配线等领域得到了广泛的应用。在PMLSM的控制系统中,控制方案大都需要测量动子的速度和位置信息。目前,PMLSM伺服控制中广泛使用光栅尺作为位置传感器。但是光栅尺不仅安装成本高,后期的维护与检修同样也会增加运行成本。除此之外,也会增加PMLSM的空间尺寸。在某些特定的环境中,并没有空间安装光栅尺等大尺寸的传感器[1]。

以上文献虽然使用了不同的无传感器技术,但是对于位置估算均是利用速度积分,存在偏差累积问题。对此,本文建立了PMLSM速度、电流双闭环矢量控制模型,并且以滑模观测器为例,仿真验证了无传感器技术的速度误差与由此带来的位置估算误差,并且从应用角度提出了一种新的低成本且高精度PMLSM位置校正策略,仿真验证了其校正效果。
1 PMLSM数学模型
在建立PMLSM的模型数学之前,先做如下假设:
(1) 忽略PMSLM中磁路饱和影响;
(2) 不考虑PMSLM中铁心的磁滞现象及涡流损耗;
(3) 不考虑PMLSM的端部效应影响;
(4) 定子电动势以正弦规律变化,不考虑 PMLSM中高次谐波的影响。
以上述假设为前提,PMLSM在dq坐标系下的非线性数学模型描述如下:
电压方程:
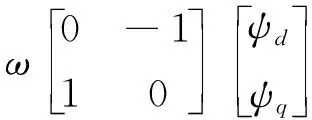
(1)
式中:ud、uq分别为d、q轴电压;Rs为定子绕组电阻;id、iq分别为d、q轴电流;ψd、ψq分别为d、q轴磁链;ω为电机电角速度。
磁链方程:

(2)
式中:ψpm为永磁体磁链;Ld为d轴同步电感;Lq为q轴同步电感。
推力方程:

(3)
式中:τ为电机极距;ψpm为永磁体磁链;p为电枢极对数。
对于表贴式PMLSM,Ld=Lq,本文研究表贴式PMLSM,因此式(3)简化为

(4)
机械方程:

(5)
式中:Fe为电磁推力;Mn为动子质量;Bn为黏滞摩擦力系数;v为动子速度且有v=ωτ/π;Fd为负载。
2 滑模观测器
滑模变结构观测器与其他方法最大的差异在于系统是动态变化的,根据系统当前的状态,迫使系统按照预定的“滑动模态”的状态轨迹运动。
为方便建立PMLSM的滑模观测器,需要将PMLSMdq坐标系模型通过2r-2s变换到αβ坐标系。 该坐标系下电压方程如下:

(6)

Eα、Eβ满足:
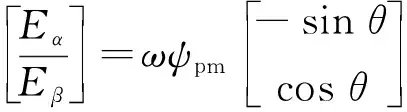
(7)
为便于应用滑模观测器观测反电动势,将式(6)改写为电流状态方程:

(8)
式中:
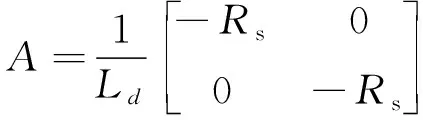
(9)
为获得反电动势估计值,设计滑模观测器如下:

(10)
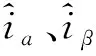
将式(10)和式(9)作差,可得电流误差方程为

(11)
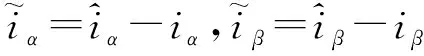
设计滑模控制率为
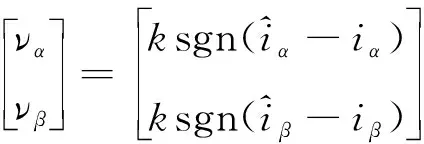
(12)


(13)
由于实际控制量是不连续的高频信号,为提取反电动势估计值,需要外加一个低通滤波器。
经过滤波以后对于电角速度则有:

(14)
PMLSM的线速度则有:

(15)
3 动子位置估算与校正
目前PMLSM无传感器控制系统主要是利用对速度积分估算动子位置。但是由于速度源自于无传感器技术,与电机实际速度之间仍然存在微小的误差。对该速度信号积分势必会造成动子位置计算误差。随着电机连续运行,偏差量也会累积。而且仅开环计算,也无法保证位置估算结果与实际位置的误差收敛,甚至会发散,导致基于无传感器控制的位置伺服系统失去意义,限制了无传感器技术在PMLSM上的应用。
针对这一现状,本文提出一种低成本高精度的校正策略,如图1所示。在定子侧,动子高频经过位置固定一枚高采样频率的光电式传感器并记录其安装位置B,当动子上的位置参考点与传感器位置重合时,该传感器动作,DSP或者其他控制器接收到外部中断,将此时的估算位置与传感器坐标B作差,并且将偏差量注入到位置估算结果中,实现了对于估算位置的校正。随着电机的连续运行,动子每一次经过该位置,估算位置就会被校正一次,提高了无传感器位置估算结果的精度,有效地避免了由于偏差累积而导致无传感器系统崩溃的风险。

图1 动子位置校正
位置估算为

(16)

当动子到达传感器位置B时:

(17)
式中:t为动子到达B位置时,DSP或控制器收到传感器中断信号的时间。

(18)
式中:Δx为动子到达传感器位置时,无传感器技术估算位置与位置B的误差。
校正后的估算位置:

(19)



图2 误差计算
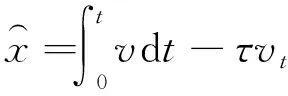
(20)
式中:vt为DSP接收到外部中断的瞬间无传感器技术观测到的速度;τ为传感器响应时间。


(21)
通过式(21)对二者位置偏差计算,并且将偏差注入到估算结果:

(22)
由此实现了PMLSM位置的校正,提高了PMLSM位置估算结果的精度,避免了估算结果与实际位置之间发散导致伺服系统崩溃的风险。该位置校正策略,为无传感器技术在PMLSM位置伺服系统的使用提供了保障。虽然增加了一枚“坐标”传感器,但是成本与体积比常用的光栅尺而言具有极强的优势,尤其是对于长定子PMLSM或者精度要求不太高的场景具有重要意义。
4 系统MATLAB仿真
在MATLAB/Simulink中搭建PMLSM速度、电流双闭环矢量控制系统与滑模观测器,如图3所示。PMLSM模型参数为,Rs=2.65 Ω、Ld=Lq=26.7 mH、ψpm=0.303 1 Wb、τ=0.016 m、Mn=28 kg、Bn=4 N·s·m-1。

图3 PMLSM控制系统
仿真条件为直流侧电压Udc=311 V,SVPWM开关频率为10 kHz,电机初始位置为0 m。初始时刻给定速度为0.6 m/s,达到给定速度后,在0.5 s时,给定阶跃为0.8 m/s,研究该连续变速运动过程中估算位置与实际位置的偏差。假设在定子侧0.5 m处安装前文所述的传感器,仿真中通过在电机实际位置到达0.5 m时,触发校正系统,实现对于传感器的模拟。根据传感器坐标与该时刻的无传感器技术估算位置求取偏差并且对位置估算结果进行校正,实现了基于传感器的校正系统仿真模拟,并且验证了校正效果。
图4为电机实际速度,图5为滑模观测器的观测速度,图6为二者的速度误差,虽然很小,但是对于位置估算而言,不能忽略。

图4 电机速度

图5 滑模观测器速度

图6 滑模观测器的速度误差
图7为未校正的动子实际位置与滑模观测器估算位置,可以看出随着电机的连续运行,由于速度误差的影响,二者之间的位置误差累积,使得PMLSM位置伺服系统性能下降。图8为采用了该校正策略后的结果,在动子到达0.5 m处,触发了校正系统,求得偏差量并且注入估算结果中,实现了动子位置校正,清除了在此之前积累的历史偏差。提高了估算结果的精度,也避免了偏差累积造成控制系统崩溃的风险。

图7 无校正的动子位置与估算位置

图8 校正后动子位置与估算位置
图9为无校正系统的位置估算误差与校正后的位置估算误差对比。可以看出,随着电机连续运行,无校正系统的位置估算误差开始发散,导致位置估算结果的精度下降。在0.5 m处触发校正系统后,清除了之前积累的偏差,与无校正系统的位置估算误差相比,校正后误差更小,大幅度提升了位置估算结果的精度。

图9 无校正与校正后位置估算误差
5 结 语
由于目前的PMLSM无传感器控制系统主要是通过速度积分估算动子位置。但是该速度与实际速度之间仍存在误差,积分会造成偏差量的累积,而且是开环计算,本身不具备校正能力。本文提出在PMLSM无传感器控制系统的定子侧动子高频经过的位置安装一枚传感器,实现类似“行程开关”的功能,每一次动子到达该位置时,都能触发校正系统,清除历史偏差,提升了位置估算系统精度的同时,也保证了控制系统不会因为位置估算误差发散而使控制系统崩溃。与传统光栅尺等传感器相比,成本低、体积小、质量轻,为一些精度要求不高的位置伺服系统和长定子PMLSM提供了更具性价比的选择。

