一种改进定子磁链观测的三相感应电机控制系统

刘占军

(上海儒竞智控技术有限公司，上海 200438)

0 引 言

磁链计算是感应电机控制的重要环节，磁链计算不准确会导致控制电压出现偏差，并导致感应电机转矩、转速、电流的控制出现问题，严重情况下会导致系统失控。电压模型是定子磁链计算的一种基本方法，其对电机参数依赖性较小，且原理简单，运算量小。采用纯积分器计算磁链，直流偏移会导致积分环节出现饱和；积分运算结果随输入正弦信号的初值不同而不同，会使得结果出现偏差。

为了解决上述问题，出现了采用低通滤波器代替理想积分器的方法，但是低通滤波器会导致幅值和相位误差问题，需要对运算结果进行幅值和相位补偿。文献[1-2]提出将磁链参考值的低通滤波信号用以补偿低通滤波环节引入的相位滞后，并发展为自适应反馈的积分器可以较好地解决纯积分环节造成的结果偏差。文献[3]提出电流和电压的混合模型以解决上述问题。文献[4]提出了采用观测器以解决磁链观测问题。文献[5]在低通滤波器后增加了幅值和相位补偿环节，提高了全速度范围下低通滤波器的准确性。文献[6-8]在文献[5]基础上提出改进，调换低通滤波器与补偿环节的顺序，提高了算法在转速突变时的稳定性。上述各种改进方案存在原理计算复杂、计算时间长和时间开销大的问题。

本文结合感应电机的数学模型对磁链观测进行改进，基于理想磁链为反电动势的微分、磁链与反电动势正交、磁链转速与反电动势转速一致思想直接计算定子磁链，经过仿真验证，该方法能够计算出理想磁链，且动态性较好。

1 定子磁链估算模型

1.1 传统估算方法及问题

三相感应电机基于电压模型的定子磁链反电动势积分表达式如下：

(1)

式中:Ψs、us、Rs、is分别为定子磁链、定子电压、定子电阻和定子电流。

该方法仅与电机定子电阻参数Rs相关，对电机参数的依赖性较小，鲁棒性好。式(1)仅采用了积分运算，结构简单，运算量小，但是当输入信号存在直流偏置时，会不断累积造成结果误差,且计算结果与输入信号的相位不同，也会造成磁链观测误差。

1.2 改进定子磁链计算方法

在正弦稳态情况下或定子磁链幅值变化较小时，式(1)可进一步推导：

us-Rsis=Es=pΨs≈jωeΨs

(2)

式中：Es为定子反电动势;p为微分算子；ωe为定子磁链角速度。

将式(2)进一步进行推导得到式(3)：

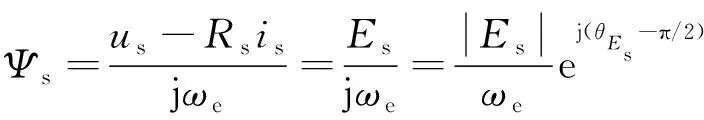
(3)

式中:|Es|、θEs分别为感应电机定子反电动势的幅值及其相角。

将式(3)的幅值和相角进行进一步分解得到式(4)和式(5)：

(4)

θΨs=θEs-π/2

(5)

式中:|Ψs|、θΨs分别为感应电机定子磁链幅值及其相角。

从式(4)和式(5)可以看到，得到电机定子反电动势的幅值、电频率和相角就可以得到定子磁链的幅值和相角。

1.3 定子磁链计算实现方法

式(2)在静止两相坐标系下的表达方式如下：

uα-Rsiα=esα

(6)

uβ-Rsiβ=esβ

(7)

式中:esα、esβ分别为感应电机定子反电动势在αβ坐标系下瞬时值。

通过对反电动势esα和esβ进行锁相环(PLL)处理可以获得定子反电动势的角频率和角度。

其中PLL的计算式如下：

(8)

式中:ed、eq为两相旋转dq轴坐标系下的反电动势。

当eq=0时，图1中的ωe将实时跟踪定子电角频率，θEs将实时跟踪定子反电动势的相角。

图1 PLL原理图

定子反电动势模|Es|计算式为

(9)

通过图1 PLL得到定子反电动势的角频率和角度，结合式(9)，应用式(4)和式(5)可以解算出感应电机的定子磁链。

1.4 改进磁链计算方法仿真

为了评价改进磁链计算方法的有效性，在理想情况下对传统方法与改进方法的计算效果进行了仿真对比。

图2对比了输入信号存在偏置时，2种算法的计算结果。其中反电动势的幅值为100 V，频率为20 Hz，esα和esβ的偏置值均为5 V。从仿真结果上可以看到，当反电动势存在直流偏置，采用传统积分方法，其磁链计算结果误差逐渐变大，而本文中提到的改进计算方法不会对直流偏置产生累积，输入直流偏置对结果影响较小。

图2 输入存在直流偏置计算结果对比

图3对比了不同输入信号相位时，2种算法的计算结果。其中反电动势的幅值为100 V，频率为20 Hz，esα和esβ的初始相位分别为0°和-90°。β轴磁链计算图形中2条曲线初始不重合的部分为PLL自动调节过程，当调节过程完毕，2条曲线重合。由此可以看到改进磁链算法不受反电动势相位的影响，可以较好地计算出反电动势数据。

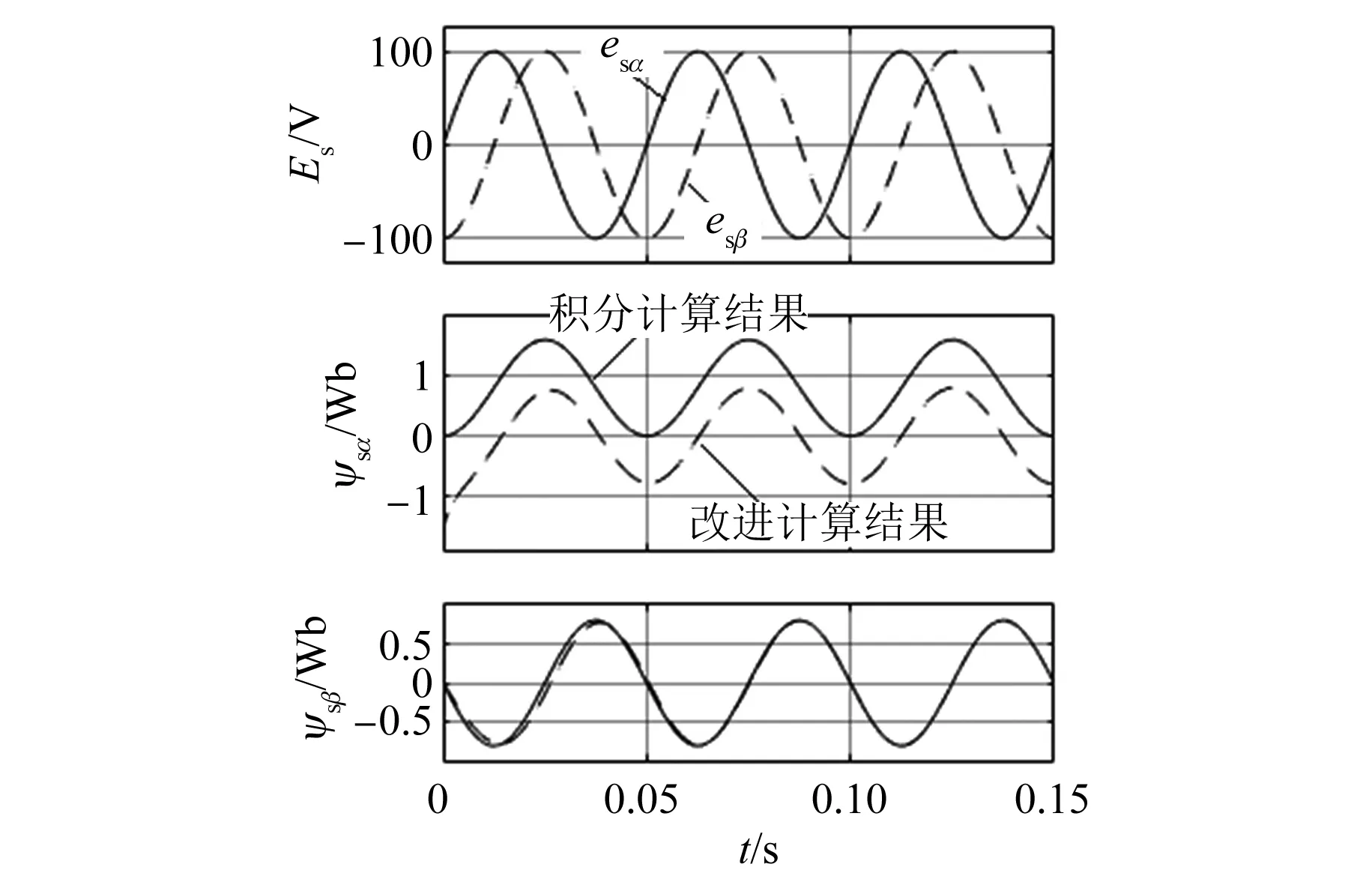
图3 输入不同相位计算结果对比

2 系统仿真验证

为了验证新方法的有效性，建立了电机驱动系统的仿真模型，其原理框图如图4所示。其中转子磁链、iq电路和转速计算方法在文献[3]和文献[9]中均有详细介绍，此处不再赘述。

图4 改进磁链观测系统仿真框图

仿真时，PWM逆变器的载波频率为6 500 Hz，控制和磁链控制计算频率也均为6 500 Hz，仿真三相感应电机参数为MATLAB内调用的默认参数，如表1所示。

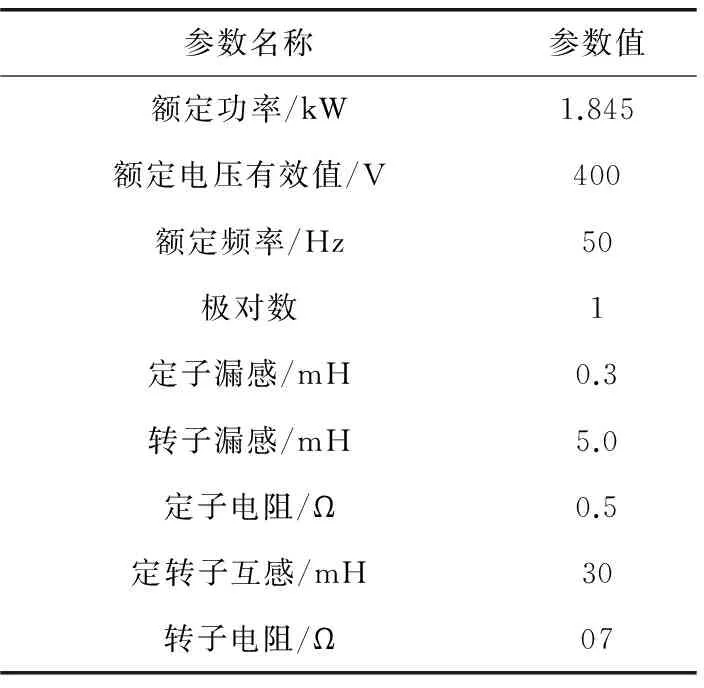
表1 仿真感应电动机参数

图5是基于改进定子磁链观测的无传感器矢量控制转速突变时的仿真结果，在5.1 s时，将转速由10 r/s提升为20 r/s。

图5 改进磁链观测系统转速突变仿真图

图6是基于改进定子磁链观测的无传感器矢量控制在负载转矩突变时的仿真结果，从上到下的波形依次为,定子磁链幅值误差、定子磁链角度误差、给定/实际转速、负载转矩和dq坐标系下电流。在t=10 s时，将负载转矩由1.5 N·m提升为2.5 N·m。从图6中可以看到该算法具有较好的动静态性能，定子磁链幅值误差、相角误差、速度稳定误差和波动均非常小。

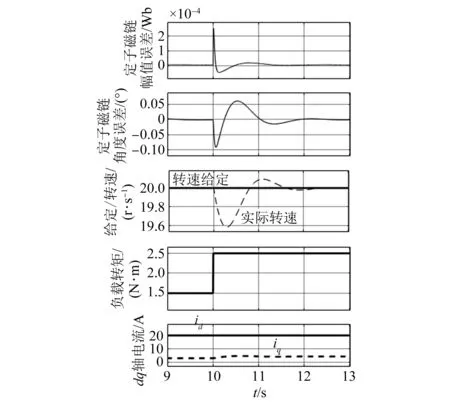
图6 改进磁链观测系统负载突变仿真图

3 结 语

在交流感应电机磁链计算工程中，传统磁链电压模型计算方法由于积分，磁链数据计算结果存在饱和与偏置。为了解决上述问题，本文提出了一种新的磁链计算方法，通过对电机定子反电动势直接进行锁相得到定子磁链的转速和角度，并结合根据定子反电动势的模直接计算电机定子磁链的幅值和角度，该方法结构简单，计算量小，非常适合于电机驱动的工程应用。